图论基本概念

一、顶点（vertex）

带数字的点就是顶点，表示某个事物或对象。由于图的术语没有标准化，可以称顶点为点、节点、结点、端点等。

顶点的度=入度+出度

二、边（edge）

顶点之间的线条就是边，表示事物与事物之间的关系。 边表示的是顶点之间的逻辑关系

三、同构（Isomorphism ）

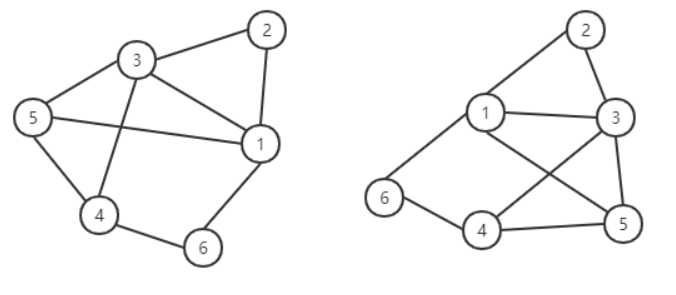
image.png

从图（graph）的角度出发，这2个图是一样的，即它们是同构的。

这些图拥有相同的信息，是同一个图。同构的图区别仅在于画法不同。

四、有向/无向图（Directed Graph/ Undirected Graph）

最基本的图通常被定义为“无向图”，与之对应的则被称为“有向图”。两者唯一的区别在于，有向图中的边是有方向性的。 下图即是一个有向图，边的方向分别是：(1->2), (1-> 3), (3-> 1), (1->5), (2->3), (3->4), (3->5), (4->5), (1->6), (4->6)。要注意，图中的边(1->3)和(3->1)是不同的。有向图和无向图的许多原理和算法是相通的。

image.png

五、权重（weight）

边的权重（或者称为权值、开销、长度等），也是一个非常核心的概念，即每条边都有与之对应的值。

有时候为了应对特殊情况，边的权重可以是零或者负数。

六、路径/最短路径（path/shortest path）

在图上任取两顶点，分别作为起点（start vertex）和终点（end vertex），我们可以规划许多条由起点到终点的路线。不会来来回回绕圈子、不会重复经过同一个点和同一条边的路线，就是一条“路径”。两点之间存在路径，则称这2个顶点是连通的（connected）。

路径也有权重。路径经过的每一条边，沿路加权重，权重总和就是路径的权重（通常只加边的权重，而不考虑顶点的权重）。在路网中，路径的权重，可以想象成路径的总长度。在有向图中，路径还必须跟随边的方向。
值得注意的是，一条路径包含了顶点和边，因此路径本身也构成了图结构，只不过是一种特殊的图结构。

七、环（loop）

环，也成为环路，是一个与路径相似的概念。在路径的终点添加一条指向起点的边，就构成一条环路。通俗点说就是绕圈。

八、连通图/连通分量（connected graph/connected component）

如果在图G中，任意2个顶点之间都存在路径，那么称G为连通图。

image.png

上面这张图中，顶点8和顶点2之间就不存在路径，因此它不是一个连通图，当然该图中还有很多顶点之间不存在路径。

上图虽然不是一个连通图，但它有多个连通子图：1,2,3顶点构成一个连通子图，1,2,3,4,5顶点构成的子图是连通图，6,7,8,9顶点构成的子图也是连通图，当然还有很多子图。

一个图的最大连通子图称为它的连通分量。1,2,3,4,5顶点构成的子图就是该图的最大连通子图，也就是连通分量。

连通分量有如下特点：

  • 是子图
  • 子图是连通的
  • 子图含有最大顶点数

注意：最大连通子图（连通分量）是其本身。

图的表示

  1. // 图的接口
  2. public interface Graph {
  4.     public int V();
  5.     public int E();
  6.     public void addEdge(int v, int w);
  7.     boolean hasEdge(int v, int w);
  8.     void show();
  9.     public Iterable<Integer> adj(int v);
  10. }

1. 邻接矩阵

  • 邻接矩阵表示无向图

image.png

  • 邻接矩阵表示有向图

image.pngimage.png

  1. /**
  2.  * 稠密图-邻接矩阵
  3.  */
  4. public class DenseGraph {
  6.     private int n;  // 节点数
  7.     private int m;  // 边数
  8.     private boolean directed;   // 是否为有向图
  9.     private boolean[][] g;      // 图的具体数据
  11.     // 构造函数
  12.     public DenseGraph( int n , boolean directed ){
  13.         assert n >= 0;
  14.         this.n = n;
  15.         this.m = 0;    // 初始化没有任何边
  16.         this.directed = directed;
  17.         // g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
  18.         // false为boolean型变量的默认值
  19.         g = new boolean[n][n];
  20.     }
  22.     public int V(){ return n;} // 返回节点个数
  23.     public int E(){ return m;} // 返回边的个数
  25.     // 向图中添加一个边
  26.     public void addEdge( int v , int w ){
  28.         assert v >= 0 && v < n ;
  29.         assert w >= 0 && w < n ;
  31.         if( hasEdge( v , w ) ){
  32.             return; 
  33.         }
  36.         g[v][w] = true;
  37.         if( !directed ){
  38.             g[w][v] = true;
  39.         }
  40.         m ++;
  41.     }
  43.     // 验证图中是否有从v到w的边
  44.     boolean hasEdge( int v , int w ){
  45.         assert v >= 0 && v < n ;
  46.         assert w >= 0 && w < n ;
  47.         return g[v][w];
  48.     }
  50.     //遍历邻边
  51.     //返回图中一个顶点的所有相邻顶点
  52.     public Iterable<Integer> adj(int v) {
  53.         assert v >= 0 && v < n;
  54.         Vector<Integer> adjV = new Vector<Integer>();
  55.         for(int i = 0 ; i < n ; i ++ )
  56.             if( g[v][i] )
  57.                 adjV.add(i);
  58.         return adjV;
  59.     }
  60. }

2. 邻接表

  • 邻接表表示无向图

image.png

  • 邻接表表示有向图

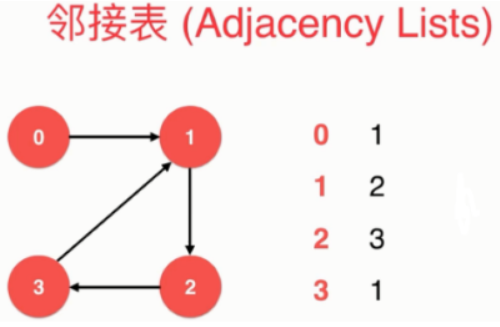
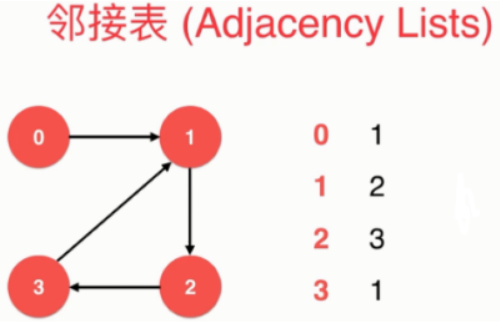
image.pngimage.png
image.png

  1. /**
  2. * 稀松图-领接表
  3. */
  4. public class SparseGraph {
  6.     private int n;  // 节点数
  7.     private int m;  // 边数
  8.     private boolean directed;    // 是否为有向图
  9.     private Vector<Integer>[] g; // 图的具体数据
  11.     // 构造函数
  12.     public SparseGraph( int n , boolean directed ){
  13.         assert n >= 0;
  14.         this.n = n;
  15.         this.m = 0;    // 初始化没有任何边
  16.         this.directed = directed;
  17.         // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
  18.         g = (Vector<Integer>[])new Vector[n];
  19.         for(int i = 0 ; i < n ; i ++){
  20.             g[i] = new Vector<Integer>();
  21.         }
  22.     }
  24.     public int V(){ return n;} // 返回节点个数
  25.     public int E(){ return m;} // 返回边的个数
  27.     // 向图中添加一个边
  28.     public void addEdge( int v, int w ){
  30.         assert v >= 0 && v < n ;
  31.         assert w >= 0 && w < n ;
  33.         g[v].add(w);
  34.         if( v != w && !directed ){
  35.             g[w].add(v);
  36.         }
  37.         m ++;
  38.     }
  40.     // 验证图中是否有从v到w的边 -->时间复杂度：O(n)
  41.     boolean hasEdge( int v , int w ){
  43.         assert v >= 0 && v < n ;
  44.         assert w >= 0 && w < n ;
  46.         for( int i = 0 ; i < g[v].size() ; i ++ ){
  47.             if( g[v].elementAt(i) == w ){
  48.                 return true;
  49.             }
  50.         }
  51.         return false;
  52.     }
  54.     //遍历邻边
  55.     //返回图中一个顶点的所有相邻顶点
  56.     public Iterable<Integer> adj(int v){
  57.         assert v>=0 && v<n;
  58.         return g[v];
  59.     }
  60. }

图的深度优先遍历（DFS）

深度优先搜索（DFS）：从某个顶点v0出发，访问此顶点，然后依次从v0的未被访问的邻接点出发递归地进行同样的DFS，直至图中和v0有路径相通的顶点都被访问，若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

  1. /**
  2.  * 图的深度优先遍历
  3.  */
  4. public class DepthFirstPaths {
  5.     //标记顶点是否被访问过
  6.     private boolean[] visited;
  7.     //记录路径
  8.     private int[] edgeTo;
  9.     //起点
  10.     private int s;
  12.     public DepthFirstPaths(Graph graph,int s){
  13.         visited=new boolean[graph.V()];
  14.         edgeTo=new int[graph.V()];
  15.         for(int i=0;i<graph.V();i++){
  16.             edgeTo[i]=-1;
  17.         }
  18.         this.s=s;
  19.         dfs(graph,this.s);
  20.     }
  22.     //深度优先搜索
  23.     private void dfs(Graph graph,int v){
  24.         visited[v]=true;
  25.         for(int w:graph.adj(v)){
  26.             if(!visited[w]){
  27.                 edgeTo[w]=v; //w--->v的路径
  28.                 dfs(graph,w);
  29.             }
  30.         }
  31.     }
  33.     //是否有到顶点v的路径
  34.     private boolean hasPathTo(int v){
  35.         return visited[v];
  36.     }
  38.     //获取从 s->v 的路径
  39.     public Iterable<Integer> pathTo(int v){
  40.         if(!hasPathTo(v)){
  41.             return null;
  42.         }
  43.         Stack<Integer> path=new Stack<>();
  44.         for(int i=v;i!=s;i=edgeTo[i]){
  45.             path.push(i);
  46.         }
  47.         path.push(s);
  48.         return path;
  49.     }
  51.     public void showPath(int v){
  52.         Stack<Integer> path= (Stack<Integer>) pathTo(v);
  54.         StringBuffer sb=new StringBuffer();
  55.         sb.append("[");
  56.         while(!path.isEmpty()){
  57.             int w=path.peek();
  58.             if(path.size()==1){
  59.                 sb.append(w);
  60.                 path.pop();
  61.             }else{
  62.                 sb.append(w+"-->");
  63.                 path.pop();
  64.             }
  65.         }
  66.         sb.append("]");
  67.         System.out.println(sb.toString());
  68.     }
  69. }

时间复杂度：

  • 领接表：O(V+E)
  • 邻接矩阵：O(V^2)

统计图的连通分量

  1. /**
  2.  * 图的dfs应用之统计图的连通分量
  3.  */
  4. public class Component {
  5.     private Graph graph;
  6.     //连通分量的个数
  7.     private int num;
  8.     private boolean[] visited;
  10.     public Component(Graph graph){
  11.         this.graph=graph;
  12.         visited=new boolean[graph.V()];
  13.         num=0;
  14.         for(int i=0;i<graph.V();i++){
  15.             if(!visited[i]){
  16.                 dfs(i);
  17.                 num++;
  18.             }
  19.         }
  20.     }
  22.     private void dfs(int v){
  23.         visited[v]=true;
  24.         for(int w:graph.adj(v)){
  25.             if(!visited[w]){
  26.                 dfs(w);
  27.             }
  28.         }
  29.     }
  31.     //获取连通分量个数
  32.     public int getNum(){
  33.         return num;
  34.     }
  35. }

图的广度优先遍历（BFS）

广度优先搜索（BFS）：从某个顶点v0出发，访问此顶点之后依次访问v0的各个未访问的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问，直至图中所有已被访问的顶点的邻接点都被访问到，若此时图中尚有顶点未被访问，则从另一个未被访问的顶点作为起点，重复上述过程，直到图中所有顶点均被访问过为止。

  1. /**
  2.  * 图的广度优先遍历
  3.  */
  4. public class BreadthFirstPaths {
  5.     //标记顶点是否被访问过
  6.     private boolean[] visited;
  7.     //记录路径
  8.     private int[] edgeTo;
  9.     //起点
  10.     private int s;
  12.     public BreadthFirstPaths(Graph graph, int s){
  13.         visited=new boolean[graph.V()];
  14.         edgeTo=new int[graph.V()];
  15.         for(int i=0;i<graph.V();i++){
  16.             edgeTo[i]=-1;
  17.         }
  18.         this.s=s;
  19.         bfs(graph,this.s);
  20.     }
  22.     //广度优先搜索
  23.     private void bfs(Graph graph,int s){
  24.         visited[s]=true;
  25.         Queue<Integer> queue=new LinkedList<>();
  26.         queue.add(s);
  27.         while (!queue.isEmpty()){
  28.             int v=queue.poll();
  29.             for(int w:graph.adj(v)){
  30.                 if(!visited[w]){
  31.                     visited[w]=true;
  32.                     edgeTo[w]=v;
  33.                     queue.add(w);
  34.                 }
  35.             }
  36.         }
  37.     }
  39.     //是否有到顶点v的路径
  40.     private boolean hasPathTo(int v){
  41.         return visited[v];
  42.     }
  44.     //获取从 s->v 的路径
  45.     public Iterable<Integer> pathTo(int v){
  46.         if(!hasPathTo(v)){
  47.             return null;
  48.         }
  49.         Stack<Integer> path=new Stack<>();
  50.         for(int i=v;i!=s;i=edgeTo[i]){
  51.             path.push(i);
  52.         }
  53.         path.push(s);
  54.         return path;
  55.     }
  57.     public void showPath(int v){
  58.         Stack<Integer> path= (Stack<Integer>) pathTo(v);
  60.         StringBuffer sb=new StringBuffer();
  61.         sb.append("[");
  62.         while(!path.isEmpty()){
  63.             int w=path.peek();
  64.             if(path.size()==1){
  65.                 sb.append(w);
  66.                 path.pop();
  67.             }else{
  68.                 sb.append(w+"-->");
  69.                 path.pop();
  70.             }
  71.         }
  72.         sb.append("]");
  73.         System.out.println(sb.toString());
  74.     }
  75. }

无权图的最短路径