什么是哈希表

哈希表（Hash table，散列表），是根据关键码值(Key value)而直接进行访问的数据结构。
也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。
这个映射函数叫做哈希函数，存放记录的数组叫做散列表。
给定表M，存在函数f(key)，对任意给定的关键字值key，
代入函数后若能得到包含该关键字的记录在表中的地址，则称表M为哈希(Hash）表，函数f(key)为哈希(Hash) 函数。

举个例子：统计 s=”fsgererhgerh”中字符出现次数（其中s只包含小写字母）

我们通常会使用这样的数组： int[] freq=new int[26];

这个freq就是一个哈希表

其中每一个字符都和一个索引对应：

image.png

哈希表设计思想：

  • 哈希表充分体现了算法设计领域的经典思想：空间换时间。
  • 哈希表是空间和时间之间的平衡
  • 哈希函数的设计十分重要
  • “键”通过哈希函数得到的“索引”分布越均匀越好

哈希函数的设计

哈希函数设计原则：

1.一致性：如果a==b,则hash(a)==hash(b)，反之，则不成立

2.高效性：计算高效简便

3.均匀性：哈希值均匀分布

整数

  • 小范围正整数：

直接使用

  • 小范围负整数：

进行偏移，比如[-100,100]，左右区间都+100，进行偏移，得到[0,200]

  • 大整数：比如身份证号 342401199607198888

通常做法：取模

1.取后4位，相当于 mod 10000 —>获得 8888

2.取后6位，相当于mod 1000000 —> 获得 198888，但是获取的数据不可能超过32万，
因为在身份证中19为表示的是一个月的某一天，最大值是31，即所谓分布不均匀问题;
只取后6位，就没有利用所有信息。

3.解决2中的两个问题的简单解决办法：模一个素数

浮点型

浮点型在计算机中也是32位或者64位的二进制表示的，只不过是计算机解析成浮点数的，
因此，可以根据浮点数的二进制表示，转化为整数。

字符串

转换成整型处理

“163” —> 1 10^2 + 6 10^1 + 3 * 10^0

“code” —> c 26^3 + o 26^2 + d 26^1 + e 26^0

“code”也可以这样转换：

“code” —> c B^3 + o B^2 + d B^1 + e B^0

(26和B都是进制，合理选择进制即可)

因此有如下哈希函数：

hash(“code”)= (c B^3 + o B^2 + d B^1 + e B^0) % M

进一步转化：

hash(“code”)= (((c _ B + o)_B + d)*B + e) % M

(((c _ B + o)_B + d)*B + e)数据有可能过大，再进一步进行转化：

hash(“code”)= ((((c % M) B + o) % M B + d) %M * B + e) % M

对应代码如下：

  1. int hash=0;
  2. for(int i=0;i<s.length();i++){
  3.     hash=( hash * B + s.charAt(i) )%M;
  4. }

复合类型

转化成整型处理

比如：对于自定义的Date

  1. class Date{
  2.     int year;
  3.     int month;
  4.     int day;
  5. }

hash(date)=(((date.year % M ) B + date.month ) % M B + date.day) % M

  • 注意：以上都是都是转化为整型处理，但这并不是唯一的方法。

Java中hashCode方法

  • Java中hashCode函数的使用
  1. public class Main {
  2.     public static void main(String[] args) {
  3.         Integer a=new Integer(3);
  4.         System.out.println(a.hashCode()); //3
  6.         Integer b=new Integer(-3);
  7.         System.out.println(b.hashCode());//-3
  9.         Double c=new Double(123.4);
  10.         System.out.println(c.hashCode());//--641253373
  12.         String s="abcd";
  13.         System.out.println(s.hashCode());//2987074
  14.     }
  15. }
  • 在自定义对象中重写hashCode函数
  1. public class Student {
  2.     private int id;
  3.     private double score;
  4.     private String name;
  6.     public Student(int id,double score,String name){
  7.         this.id=id;
  8.         this.score=score;
  9.         this.name=name;
  10.     }
  12.     @Override
  13.     public int hashCode() {
  14.         int B=26;
  16.         int hash=0;
  17.         hash = hash * B + id;
  18.         hash = hash * B + ((Double)score).hashCode();
  19.         //忽略name的大小写问题
  20.         hash = hash * B + name.toLowerCase().hashCode();
  21.         return hash;
  22.     }
  23. }
  1. public class Main2 {
  2.     public static void main(String[] args) {
  3.         Student s=new Student(1,90.0,"aaa");
  4.         System.out.println(s.hashCode()); //-1999996187
  6.         Student s2=new Student(1,90.0,"aaa");
  7.         System.out.println(s2.hashCode());//-1999996187
  8.     }
  9. }
  • 重写equals()方法
  1. 检查是否为同一个对象的引用，如果是直接返回 true；
  2. 检查是否是同一个类型(判断Class对象是否相同)，如果不是，直接返回 false；
  3. 将 Object 对象进行转型
  4. 判断每个关键域是否相等
  1. @Override
  2. public boolean equals(Object obj) {
  3.     if(this==obj){
  4.         return true;
  5.     }
  6.     if(obj==null || this.getClass()!=obj.getClass()){
  7.         return false;
  8.     }
  9.     Student another=(Student)obj;
  10.     return this.id==another.id &&
  11.             this.score==another.score &&
  12.             this.name.toLowerCase().equals(another.name.toLowerCase());
  13. }
  1. public class Main2 {
  2.     public static void main(String[] args) {
  3.         Student s=new Student(1,90.0,"aaa");
  4.         System.out.println(s.hashCode()); //-1999996187
  6.         Student s2=new Student(1,90.0,"aaa");
  7.         System.out.println(s2.hashCode());//-1999996187
  9.         //s和s2的地址是不同的，但是内容是相同的
  10.         System.out.println(s==s2); //false
  11.         System.out.println(s.equals(s2)); //true
  12.     }
  13. }
  • 注意：Java中每个对象默认有默认的hashCode实现。hashCode就是该对象的地址。

重写hashCode的情况：

  1. Student s=new Student(1,90.0,"aaa");
  2. System.out.println(s.hashCode()); //-1999996187
  4. Student s2=new Student(1,90.0,"aaa");
  5. System.out.println(s2.hashCode());//-1999996187

未重写hashCode的情况:

  1. Student s=new Student(1,90.0,"aaa");
  2. System.out.println(s.hashCode()); //21685669
  4. Student s2=new Student(1,90.0,"aaa");
  5. System.out.println(s2.hashCode());//2133927002

s和s2的hashCode不同，因为s和s2的地址不同。

哈希冲突的处理 Seperate Chaining

  • 计算哈希值 (hashCode(k1) & 0x7fffffff) % M

image.png

  • 采用查找表解决哈希冲突，查找表也可以使用平衡树结构

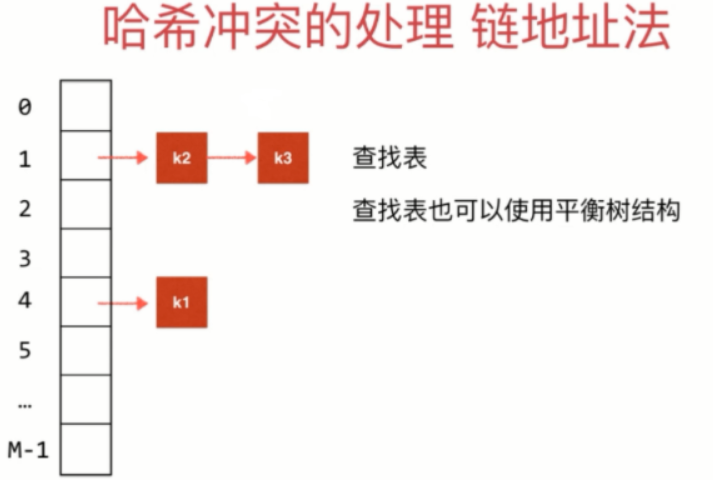
image.png

  • 使用HashMap作为查找表

image.png

  • 注意：
  1. Java 8之前，每个位置对应一个链表
  2. Java 8之后，当哈希冲突达到一定程度，每个位置从链表转成红黑树

哈希表编程

  1. public class HashTable<K,V> {
  2.     private TreeMap<K,V>[]  hashtable;
  3.     private int M;
  4.     private int size;
  6.     public HashTable(int M){
  7.         this.M=M;
  8.         this.size=0;
  9.         this.hashtable=new TreeMap[M];
  10.         for(int i=0;i<M;i++){
  11.             hashtable[i]=new TreeMap<>();
  12.         }
  13.     }
  15.     public HashTable(){
  16.         this(97);
  17.     }
  19.     private int hash(K key){
  20.         return (key.hashCode() & 0x7fffffff) % M;
  21.     }
  23.     public int getSize(){
  24.         return size;
  25.     }
  26. }
  • 哈希表具体功能实现
  1. public void add(K key,V value){
  2.     TreeMap<K,V> map=hashtable[hash(key)];
  3.     if(map.containsKey(key)){
  4.         map.put(key,value);
  5.     }else{
  6.         map.put(key,value);
  7.         size++;
  8.     }
  9. }
  11. public V remove(K key){
  12.     TreeMap<K,V> map=hashtable[hash(key)];
  13.     V ret=null;
  14.     if(map.containsKey(key)){
  15.         ret=map.remove(key);
  16.         size--;
  17.     }
  18.     return ret;
  19. }
  21. public void set(K key,V value){
  22.     TreeMap<K,V> map=hashtable[hash(key)];
  23.     if(!map.containsKey(key)) {
  24.         throw new IllegalArgumentException(key + "does not exist!");
  25.     }
  26.     map.put(key,value);
  27. }
  29. public boolean contains(K key){
  30.     return hashtable[hash(key)].containsKey(key);
  31. }
  33. public V get(K key){
  34.     return hashtable[hash(key)].get(key);
  35. }
  • 哈希表链表法时间复杂度分析

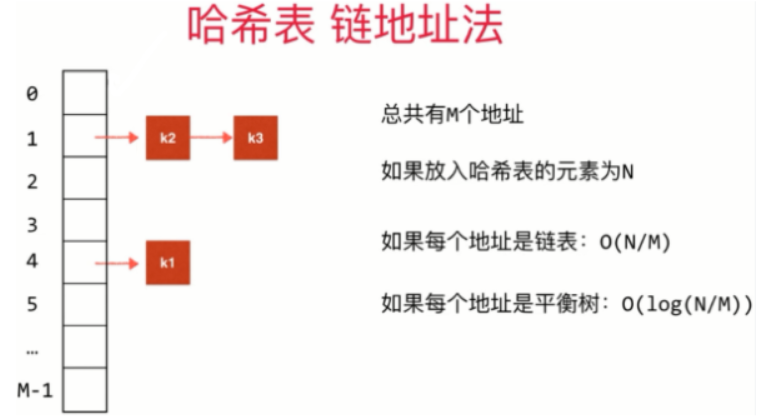
image.png

哈希表的动态空间处理

image.png

  1. public class HashTable2<K,V> {
  2.     private static final int upperTol=10;
  3.     private static final int lowerTol=2;
  4.     private static final int initCapacity=7;
  6.     private TreeMap<K,V>[]  hashtable;
  7.     private int M;
  8.     private int size;
  10.     public HashTable2(int M){
  11.         this.M=M;
  12.         this.size=0;
  13.         this.hashtable=new TreeMap[M];
  14.         for(int i=0;i<M;i++){
  15.             hashtable[i]=new TreeMap<>();
  16.         }
  17.     }
  19.     public HashTable2(){
  20.         this(initCapacity);
  21.     }
  23.     private int hash(K key){
  24.         return (key.hashCode() & 0x7fffffff) % M;
  25.     }
  27.     private void resize(int newM){
  28.         TreeMap<K,V>[] newHashtable=new TreeMap[newM];
  29.         for(int i=0;i<newM;i++){
  30.             newHashtable[i]=new TreeMap<>();
  31.         }
  33.         int oldM=M;
  34.         this.M=newM;
  35.         for(int i=0;i<oldM;i++){
  36.             TreeMap<K,V> map=hashtable[i];
  37.             for(K key:map.keySet()){
  38.                 newHashtable[hash(key)].put(key,map.get(key));
  39.             }
  40.         }
  41.         hashtable=newHashtable;
  42.     }
  44.     public int getSize(){
  45.         return size;
  46.     }
  48.     public void add(K key,V value){
  49.         TreeMap<K,V> map=hashtable[hash(key)];
  50.         if(map.containsKey(key)){
  51.             map.put(key,value);
  52.         }else{
  53.             map.put(key,value);
  54.             size++;
  55.             if(size >= upperTol*M){
  56.                 resize(2*M);
  57.             }
  58.         }
  59.     }
  61.     public V remove(K key){
  62.         TreeMap<K,V> map=hashtable[hash(key)];
  63.         V ret=null;
  64.         if(map.containsKey(key)){
  65.             ret=map.remove(key);
  66.             size--;
  67.             if(size < lowerTol*M && M/2>=initCapacity){
  68.                 resize(M/2);
  69.             }
  70.         }
  71.         return ret;
  72.     }
  74.     public void set(K key,V value){
  75.         TreeMap<K,V> map=hashtable[hash(key)];
  76.         if(!map.containsKey(key)) {
  77.             throw new IllegalArgumentException(key + "does not exist!");
  78.         }
  79.         map.put(key,value);
  80.     }
  82.     public boolean contains(K key){
  83.         return hashtable[hash(key)].containsKey(key);
  84.     }
  86.     public V get(K key){
  87.         return hashtable[hash(key)].get(key);
  88.     }
  89. }
  • 时间复杂度分析：

平均时间复杂度：O(1)

实际上每个操作的时间复杂度是：O( log(lowerTol) ) ~ O( log(upperTol) ),而lowerTol和upperTol都是常数。

优化哈希表

  1. public class HashTable3<K,V> {
  2.     //哈希表容量的常量表
  3.     private final int[] capacity = {
  4.             53, 97, 193, 389, 769, 1543, 3079, 6151, 12289, 24593,
  5.             49157, 98317, 196613, 393241, 786433, 1572869, 3145739,
  6.             6291469, 12582917, 25165843, 50331653, 100663319, 201326611,
  7.             402653189, 805306457, 1610612741};
  8.     //int类型的最大素数就是 1610612741
  10.     private static final int upperTol=10;
  11.     private static final int lowerTol=2;
  12.     private int capacityIndex=0;
  14.     private TreeMap<K,V>[]  hashtable;
  15.     private int M;
  16.     private int size;
  18.     public HashTable3(){
  19.         this.M=capacity[capacityIndex];
  20.         this.size=0;
  21.         this.hashtable=new TreeMap[M];
  22.         for(int i=0;i<M;i++){
  23.             hashtable[i]=new TreeMap<>();
  24.         }
  25.     }
  27.     private int hash(K key){
  28.         return (key.hashCode() & 0x7fffffff) % M;
  29.     }
  31.     private void resize(int newM){
  32.         TreeMap<K,V>[] newHashtable=new TreeMap[newM];
  33.         for(int i=0;i<newM;i++){
  34.             newHashtable[i]=new TreeMap<>();
  35.         }
  37.         int oldM=M;
  38.         this.M=newM;
  39.         for(int i=0;i<oldM;i++){
  40.             TreeMap<K,V> map=hashtable[i];
  41.             for(K key:map.keySet()){
  42.                 newHashtable[hash(key)].put(key,map.get(key));
  43.             }
  44.         }
  45.         hashtable=newHashtable;
  46.     }
  48.     public int getSize(){
  49.         return size;
  50.     }
  52.     public void add(K key,V value){
  53.         TreeMap<K,V> map=hashtable[hash(key)];
  54.         if(map.containsKey(key)){
  55.             map.put(key,value);
  56.         }else{
  57.             map.put(key,value);
  58.             size++;
  59.             if(size >= upperTol*M && capacityIndex+1<capacity.length){
  60.                 capacityIndex++;
  61.                 resize(capacity[capacityIndex]);
  62.             }
  63.         }
  64.     }
  66.     public V remove(K key){
  67.         TreeMap<K,V> map=hashtable[hash(key)];
  68.         V ret=null;
  69.         if(map.containsKey(key)){
  70.             ret=map.remove(key);
  71.             size--;
  72.             if(size < lowerTol*M && capacityIndex-1>=0){
  73.                 capacityIndex--;
  74.                 resize(capacity[capacityIndex]);
  75.             }
  76.         }
  77.         return ret;
  78.     }
  80.     public void set(K key,V value){
  81.         TreeMap<K,V> map=hashtable[hash(key)];
  82.         if(!map.containsKey(key)) {
  83.             throw new IllegalArgumentException(key + "does not exist!");
  84.         }
  85.         map.put(key,value);
  86.     }
  88.     public boolean contains(K key){
  89.         return hashtable[hash(key)].containsKey(key);
  90.     }
  92.     public V get(K key){
  93.         return hashtable[hash(key)].get(key);
  94.     }
  95. }

设计的哈希表中的不足

image.png

Java 8之前，每一个位置对应一个链表，K不要求具有可比性,所以是无序的。

Java 8之后，当哈希冲突得到一定程度时，每一个位置从链表转化成红黑树，这时就要求K具有可比性。

开放地址法解决哈希冲突

1.线性探测法

每次遇到哈希冲突，就+1

2.平方探测法

遇到哈希冲突, 就+1

再次遇到哈希冲突，就+4

再次遇到哈希冲突，就+9

…

3.二次哈希

每次遇到哈希冲突，就 +hash2(key)

其他解决哈希冲突的方法：

  • 再哈希法 Rehashing
  • Coalesced Hashing(综合了开放地址法和链地址法)