平衡二叉树

平衡二叉树特点：对于任意一个节点，左子树和右子树的高度差不能超过1

下图就是一棵平衡二叉树：

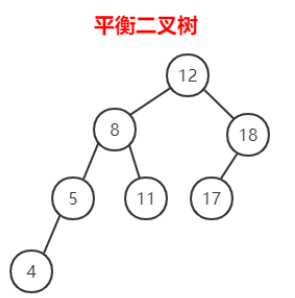
image.png

  • 标注节点的高度：(叶子节点的高度为1)

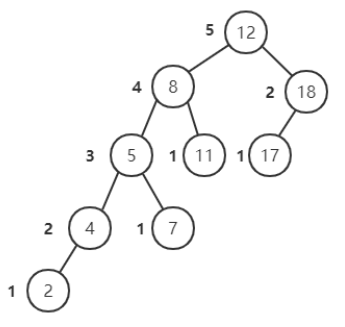
image.png

  • 计算平衡因子:(这里是根据左子树高度减去右子树高度进行计算)：

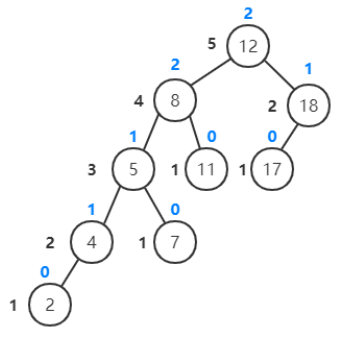
image.png

计算节点的高度和平衡因子

  1. public class AVLTree<K extends Comparable<K>,V>{
  2.     private class Node{
  3.         public K key;
  4.         public V value;
  5.         public Node left,right;
  6.         public int height;
  7.         public Node(K key,V value){
  8.             this.key=key;
  9.             this.value=value;
  10.             this.left=null;
  11.             this.right=null;
  12.             //叶子节点的高度是1
  13.             height=1;
  14.         }
  15.     }
  17.     private Node root;
  18.     private int size;
  20.     public void add(K key, V value) {
  21.         root=add(root,key,value);
  22.     }
  24.     //计算节点的高度
  25.     private int getNodeHeight(Node node){
  26.         if(node==null){
  27.             return 0;
  28.         }
  29.         return node.height;
  30.     }
  32.     //获取节点的平衡因子，左子树高度-右子树高度
  33.     private int getBalancedFactor(Node node){
  34.         if(node==null){
  35.             return 0;
  36.         }
  37.         return getNodeHeight(node.left)-getNodeHeight(node.right);
  38.     }
  40.     private Node add(Node node,K key,V value){
  41.         if(node==null){
  42.             size++;
  43.             return new Node(key,value);
  44.         }
  45.         if(key.compareTo(node.key)<0){
  46.             node.left=add(node.left,key,value);
  47.         }else if(key.compareTo(node.key)>0){
  48.             node.right=add(node.right,key,value);
  49.         }else{
  50.             node.value=value;
  51.         }
  52.         //更新height
  53.         node.height=1+Math.max(getNodeHeight(node.left),getNodeHeight(node.right));
  54.         //计算平衡因子
  55.         int balancedFactor=getBalancedFactor(node);
  56.         if(Math.abs(balancedFactor)>1){
  57.             System.out.println("unblance:"+balancedFactor);
  58.         }
  59.         return node;
  60.     }
  61. }

检查二分搜索树和平衡树

  • 利用BST中序遍历性质，判断是否是BST
  1. //检查该树是否是平衡二叉树
  2. public boolean isBST(){
  3.     List<K> keys=new ArrayList<>();
  4.     inOrder(root,keys);
  5.     for(int i=1;i<keys.size();i++){
  6.         if(keys.get(i-1).compareTo(keys.get(i))>0){
  7.             return false;
  8.         }
  9.     }
  10.     return true;
  11. }
  13. private void inOrder(Node node, List<K> keys){
  14.     if(node==null){
  15.         return;
  16.     }
  17.     inOrder(node.left,keys);
  18.     keys.add(node.key);
  19.     inOrder(node.right,keys);
  20. }
  • 判断该树是否是平衡树
  1. //判断该二叉树是否是一棵平衡二叉树
  2. public boolean isBalancedTree(){
  3.     return isBalancedTree(root);
  4. }
  6. private boolean isBalancedTree(Node node){
  7.     if(node==null){
  8.         return true;
  9.     }
  10.     int balancedFactor=getBalancedFactor(node);
  11.     if(Math.abs(balancedFactor)>1){
  12.         return false;
  13.     }
  14.     return isBalancedTree(node.left) && isBalancedTree(node.right);
  15. }

AVL树的左旋转和右旋转

  • AVL树的右旋转：插入的元素在不平衡的节点的左侧的左侧

image.png

  • 右旋转针对的情况：以x、z为根节点的子树是平衡的BST树,添加一个元素以y为根节点的子树就不是平衡二叉树了

image.png

  • 右旋转操作I:x.right=y

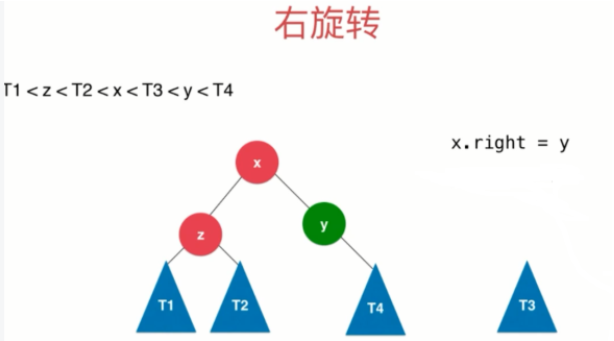
image.png

  • 右旋转操作II:y.left=T3

image.png

  • 右旋转之后，就是平衡的BST：假设z节点的高度是(h+1),可以验证以x为根节点的BST树是平衡树

image.png

  • 代码实现：
  1. // 对节点y进行向右旋转操作，返回旋转后新的根节点x
  2. //        y                              x
  3. //       / \                           /   \
  4. //      x   T4     向右旋转 (y)        z     y
  5. //     / \       - - - - - - - ->    / \   / \
  6. //    z   T3                       T1  T2 T3 T4
  7. //   / \
  8. // T1   T2
  9. private Node rightRotate(Node y){
  10.     Node x=y.left;
  11.     Node T3=x.right;
  13.     //向右旋转
  14.     x.right=y;
  15.     y.left=T3;
  17.     //维护树的高度
  18.     y.height=1 + Math.max(getNodeHeight(y.left),getNodeHeight(y.right));
  19.     x.height=1 + Math.max(getNodeHeight(x.left),getNodeHeight(x.right));
  21.     return x;
  22. }
  24. private Node add(Node node,K key,V value){
  25.     if(node==null){
  26.         size++;
  27.         return new Node(key,value);
  28.     }
  29.     if(key.compareTo(node.key)<0){
  30.         node.left=add(node.left,key,value);
  31.     }else if(key.compareTo(node.key)>0){
  32.         node.right=add(node.right,key,value);
  33.     }else{
  34.         node.value=value;
  35.     }
  36.     //更新height
  37.     node.height=1+Math.max(getNodeHeight(node.left),getNodeHeight(node.right));
  38.     //计算平衡因子
  39.     int balancedFactor=getBalancedFactor(node);
  40.     if(Math.abs(balancedFactor)>1){
  41.         System.out.println("unblance:"+balancedFactor);
  42.     }
  44.     //平衡维护-->右旋转
  45.     if(balancedFactor>1 && getBalancedFactor(node.left)>=0){
  46.         return rightRotate(node);
  47.     }
  49.     return node;
  50. }
  • AVL的左旋转
  1. // 对节点y进行向左旋转操作，返回旋转后新的根节点x
  2. //    y                             x
  3. //  /  \                          /   \
  4. // T1   x      向左旋转 (y)       y     z
  5. //     / \   - - - - - - - ->   / \   / \
  6. //   T2  z                     T1 T2 T3 T4
  7. //      / \
  8. //     T3 T4
  9. private Node leftRotate(Node y){
  10.     Node x=y.right;
  11.     Node T2=x.left;
  13.     //向左旋转
  14.     x.left=y;
  15.     y.right=T2;
  17.     //维护高度
  18.     y.height=1+Math.max(getNodeHeight(y.left),getNodeHeight(y.right));
  19.     x.height=1+Math.max(getNodeHeight(x.left),getNodeHeight(x.right));
  21.     return x;
  22. }
  24. private Node add(Node node,K key,V value){
  25.     if(node==null){
  26.         size++;
  27.         return new Node(key,value);
  28.     }
  29.     if(key.compareTo(node.key)<0){
  30.         node.left=add(node.left,key,value);
  31.     }else if(key.compareTo(node.key)>0){
  32.         node.right=add(node.right,key,value);
  33.     }else{
  34.         node.value=value;
  35.     }
  36.     //更新height
  37.     node.height=1+Math.max(getNodeHeight(node.left),getNodeHeight(node.right));
  38.     //计算平衡因子
  39.     int balancedFactor=getBalancedFactor(node);
  40.     if(Math.abs(balancedFactor)>1){
  41.         System.out.println("unblance:"+balancedFactor);
  42.     }
  44.     //平衡维护-->右旋转
  45.     if(balancedFactor>1 && getBalancedFactor(node.left)>=0){
  46.         return rightRotate(node);
  47.     }
  48.     if(balancedFactor<-1 && getBalancedFactor(node.right)<=0){
  49.         return leftRotate(node);
  50.     }
  51.     return node;
  52. }

LR和RL

  • LR

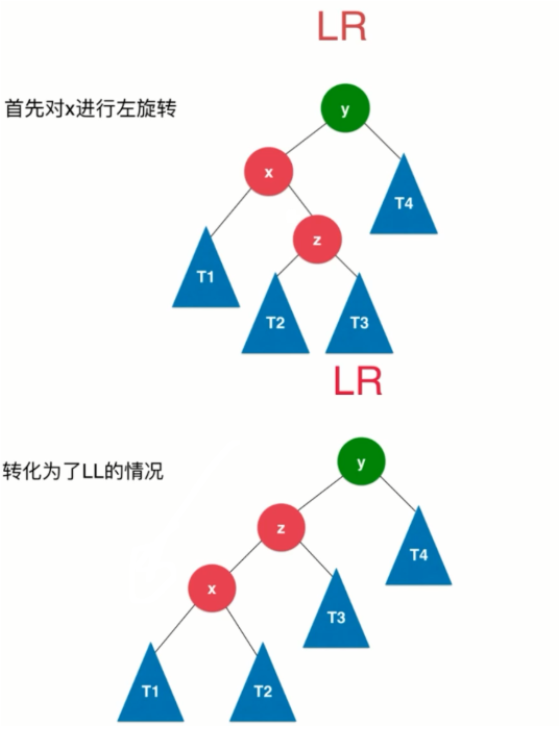
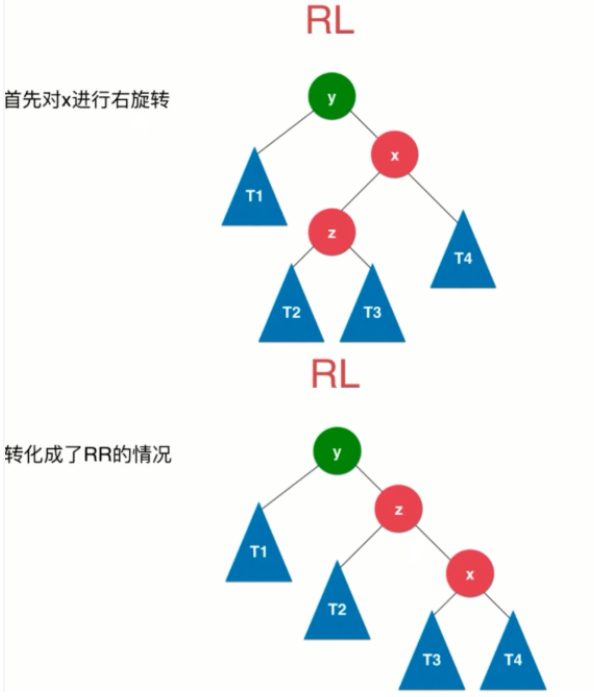
image.pngimage.png

  • RLimage.pngimage.png
  1. //计算平衡因子
  2. int balancedFactor=getBalancedFactor(node);
  3. /*if(Math.abs(balancedFactor)>1){
  4.     System.out.println("unblance:"+balancedFactor);
  5. }*/
  7. //平衡维护
  8. //LL
  9. if(balancedFactor>1 && getBalancedFactor(node.left)>=0){
  10.     return rightRotate(node);
  11. }
  12. //RR
  13. if(balancedFactor<-1 && getBalancedFactor(node.right)<=0){
  14.     return leftRotate(node);
  15. }
  16. //LR
  17. if(balancedFactor>1 && getBalancedFactor(node.left)<0){
  18.     Node x=node.left;
  19.     node.left=leftRotate(x);
  20.     //LL
  21.     return rightRotate(node);
  22. }
  23. //RL
  24. if(balancedFactor<-1 && getBalancedFactor(node.right)>0){
  25.     Node x=node.right;
  26.     node.right=rightRotate(x);
  27.     //RR
  28.     return leftRotate(node);
  29. }

删除元素

  1. //从AVL中删除值为key的元素
  2. public V remove(K key) {
  3.     Node node=getNode(root,key);
  4.     if(node!=null){
  5.         root=del(root,key);
  6.         size--;
  7.     }
  8.     return null;
  9. }
  11. //获取Map中的最小的key
  12. private Node min(Node node){
  13.     if(node.left==null){
  14.         return node;
  15.     }
  16.     return min(node.left);
  17. }
  19. //删除以node为根结点的Map中的key最小的元素
  20. private Node delMin(Node node){
  21.     if(node.left==null){
  22.         Node nodeRight=node.right;
  23.         node.right=null;
  24.         size--;
  25.         return nodeRight;
  26.     }
  27.     node.left=delMin(node.left);
  29.     //更新height
  30.     node.height=1+Math.max(getNodeHeight(node.left),getNodeHeight(node.right));
  32.     //维护平衡
  33.     return keepBalance(node);
  34. }
  36. ////删除以node为根结点的Map中的键值为key的元素
  37. private Node del(Node node, K key){
  38.     if(node==null){
  39.         return null;
  40.     }
  41.     //记录删除元素后，该BST的新的根节点
  42.     Node retNode=null;
  43.     if(key.compareTo(node.key)<0){
  44.         node.left=del(node.left,key);
  45.         retNode=node;
  46.     }else if(key.compareTo(node.key)>0){
  47.         node.right=del(node.right,key);
  48.         retNode=node;
  49.     }else{
  50.         //节点node就是要删除的节点
  51.         //该节点只右有子树
  52.         if(node.left==null){
  53.             Node rightNode=node.right;
  54.             node.right=null;
  55.             size--;
  56.             retNode=rightNode;
  57.         }else if(node.right==null){ //该节点只有左子树
  58.             Node leftNode=node.left;
  59.             node.left=null;
  60.             size--;
  61.             retNode=leftNode;
  62.         }else{
  63.             //删除既有左子树又有右子树的节点
  64.             Node s=min(node.right);
  65.             s.right=delMin(node.right);
  66.             s.left=node.left;
  68.             //删除node
  69.             node.left=node.right=null;
  70.             retNode=s;
  71.         }
  72.     }
  73.     if(retNode==null){
  74.         return retNode;
  75.     }
  76.     //更新height
  77.     retNode.height=1+Math.max(getNodeHeight(retNode.left),getNodeHeight(retNode.right));
  79.     //保持平衡
  80.     return keepBalance(retNode);
  81. }
  83. //维护以node为根节点的二叉树是平衡二叉树
  84. private Node keepBalance(Node node){
  85.     //计算平衡因子
  86.     int balancedFactor=getBalancedFactor(node);
  88.     //平衡维护
  89.     //LL
  90.     if(balancedFactor>1 && getBalancedFactor(node.left)>=0){
  91.         return rightRotate(node);
  92.     }
  93.     //RR
  94.     if(balancedFactor<-1 && getBalancedFactor(node.right)<=0){
  95.         return leftRotate(node);
  96.     }
  97.     //LR
  98.     if(balancedFactor>1 && getBalancedFactor(node.left)<0){
  99.         Node x=node.left;
  100.         node.left=leftRotate(x);
  101.         //LL
  102.         return rightRotate(node);
  103.     }
  104.     //RL
  105.     if(balancedFactor<-1 && getBalancedFactor(node.right)>0){
  106.         Node x=node.right;
  107.         node.right=rightRotate(x);
  108.         //RR
  109.         return leftRotate(node);
  110.     }
  111.     return node;
  112. }

基于AVL树的集合和映射

  • AVL Map
  1. public class AVLMap<K extends Comparable<K>,V> implements Map<K,V> {
  2.     private AVLTree<K,V> avlTree;
  4.     public AVLMap(){
  5.         avlTree=new AVLTree<>();
  6.     }
  8.     @Override
  9.     public void add(K key, V value) {
  10.         avlTree.add(key,value);
  11.     }
  13.     @Override
  14.     public V remove(K key) {
  15.         return avlTree.remove(key);
  16.     }
  18.     @Override
  19.     public boolean contains(K key) {
  20.         return avlTree.contains(key);
  21.     }
  23.     @Override
  24.     public V get(K key) {
  25.         return avlTree.get(key);
  26.     }
  28.     @Override
  29.     public void set(K key, V newValue) {
  30.         avlTree.set(key,newValue);
  31.     }
  33.     @Override
  34.     public int getSize() {
  35.         return avlTree.getSize();
  36.     }
  38.     @Override
  39.     public boolean isEmpty() {
  40.         return avlTree.isEmpty();
  41.     }
  42. }
  • AVL Set