有向边

  1. public class Edge<E extends Number & Comparable> implements Comparable<Edge>{
  2.     //定义改变的起始节点和终止节点
  3.     private int from;
  4.     private int to;
  5.     //该边的权值
  6.     private E weight;
  8.     public Edge(int v, int w, E weight)
  9.     {
  10.         this.from = v;
  11.         this.to = w;
  12.         this.weight = weight;
  13.     }
  15.     public Edge(Edge<E> e)
  16.     {
  17.         this.from = e.from;
  18.         this.to = e.to;
  19.         this.weight = e.weight;
  20.     }
  22.     //获取起点
  23.     public int v(){
  24.         return from;
  25.     }
  27.     //获取终点
  28.     public int w(){
  29.         return to;
  30.     }
  32.     //获取权值
  33.     public E wt(){
  34.         return weight;
  35.     }
  37.     // 给定一个顶点, 返回另一个顶点
  38.     public int other(int x){
  39.         assert x == from || x == to;
  40.         return x == from ? to : from;
  41.     }
  43.     //输出边的具体信息
  44.     @Override
  45.     public String toString() {
  46.         return "" + from + "-" + to + ": " + weight;
  47.     }
  49.     @Override
  50.     public int compareTo(Edge that) {
  51.         int num=weight.compareTo(that.wt());
  52.         return num;
  53.     }
  54. }

带权图

  1. // 带权图的接口
  2. public interface WeightedGraph<E extends Number & Comparable> {
  3.     public int V();
  4.     public int E();
  5.     public void addEdge(Edge<E> edge);
  6.     boolean hasEdge(int v, int w);
  7.     void show();
  8.     public Iterable<Edge<E>> adj(int v);
  9. }

稠密图(带权图)

  1. public class DenseWeightedGraph<E extends Number & Comparable> implements WeightedGraph<E>{
  3.     private int n;  // 节点数
  4.     private int m;  // 边数
  5.     private boolean directed;   // 是否为有向图
  6.     private Edge[][] g;      // 图的具体数据
  8.     // 构造函数
  9.     public DenseWeightedGraph(int n , boolean directed ){
  10.         assert n >= 0;
  11.         this.n = n;
  12.         this.m = 0;    // 初始化没有任何边
  13.         //false表示无向图
  14.         this.directed = directed;
  15.         // g初始化为n*n的有向边矩阵
  16.         g = new Edge[n][n];
  17.     }
  19.     @Override
  20.     public int V(){ return n;} // 返回节点个数
  22.     @Override
  23.     public int E(){ return m;} // 返回边的个数
  25.     // 向图中添加一个边
  26.     @Override
  27.     public void addEdge(Edge edge){
  28.         assert edge.v() >= 0 && edge.v() < n ;
  29.         assert edge.w() >= 0 && edge.w() < n ;
  31.         if( hasEdge( edge.v() , edge.w() ) ){
  32.             return;
  33.         }
  34.         g[edge.v()][edge.w()] = new Edge(edge);
  35.         if( edge.v() != edge.w() && !directed ){
  36.             g[edge.w()][edge.v()] = new Edge(edge.w(), edge.v(), edge.wt());
  37.         }
  38.         m ++;
  39.     }
  41.     // 验证图中是否有从v到w的边
  42.     @Override
  43.     public boolean hasEdge( int v , int w ){
  44.         assert v >= 0 && v < n ;
  45.         assert w >= 0 && w < n ;
  46.         return g[v][w]!=null;
  47.     }
  49.     @Override
  50.     public void show() {
  51.         for(int i=0;i<n;i++){
  52.             for(int j=0;j<n;j++){
  53.                 if(g[i][j]!=null){
  54.                     System.out.print(g[i][j].wt()+"\t");
  55.                 }else{
  56.                     System.out.print("NULL\t");
  57.                 }
  58.             }
  59.             System.out.println();
  60.         }
  61.     }
  63.     // 返回图中一个顶点的所有邻边
  64.     // 由于java使用引用机制，返回一个Vector不会带来额外开销
  65.     @Override
  66.     public Iterable<Edge<E>> adj(int v) {
  67.         assert v >= 0 && v < n;
  68.         Vector<Edge<E>> adjV = new Vector<>();
  69.         for (int i = 0; i < n; i++) {
  70.             if (g[v][i]!=null) {
  71.                 adjV.add(g[v][i]);
  72.             }
  73.         }
  74.         return adjV;
  75.     }
  76. }

稀疏图(带权图)

  1. public class SparseWeightedGraph<E extends Number & Comparable> implements WeightedGraph<E>{
  3.     private int n;  // 节点数
  4.     private int m;  // 边数
  5.     private boolean directed;    // 是否为有向图
  6.     private Vector<Edge<E>>[] g; // 图的具体数据
  8.     // 构造函数
  9.     public SparseWeightedGraph(int n , boolean directed ){
  10.         assert n >= 0;
  11.         this.n = n;
  12.         this.m = 0;    // 初始化没有任何边
  13.         this.directed = directed;
  14.         // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
  15.         g = (Vector<Edge<E>>[])new Vector[n];
  16.         for(int i = 0 ; i < n ; i ++){
  17.             g[i] = new Vector<Edge<E>>();
  18.         }
  19.     }
  21.     @Override
  22.     public int V(){ return n;} // 返回节点个数
  24.     @Override
  25.     public int E(){ return m;} // 返回边的个数
  27.     // 向图中添加一个边
  28.     @Override
  29.     public void addEdge(Edge edge){
  31.         assert edge.v() >= 0 && edge.v() < n ;
  32.         assert edge.w() >= 0 && edge.w() < n ;
  34.         g[edge.v()].add(edge);
  35.         if( edge.v() != edge.w() && !directed ){
  36.             g[edge.w()].add(new Edge(edge.w(),edge.v(),edge.wt()));
  37.         }
  38.         m ++;
  39.     }
  41.     // 验证图中是否有从v到w的边 -->时间复杂度：O(n)
  42.     @Override
  43.     public boolean hasEdge(int v, int w){
  45.         assert v >= 0 && v < n ;
  46.         assert w >= 0 && w < n ;
  48.         for( int i = 0 ; i < g[v].size() ; i ++ ){
  49.             if( g[v].elementAt(i).other(v) == w ){
  50.                 return true;
  51.             }
  52.         }
  53.         return false;
  54.     }
  56.     @Override
  57.     public void show() {
  58.         for( int i = 0 ; i < n ; i ++ ){
  59.             System.out.print("vertex " + i + ":\t");
  60.             for( int j = 0 ; j < g[i].size() ; j ++ ){
  61.                 Edge e = g[i].elementAt(j);
  62.                 System.out.print( "( to:" + e.other(i) + ",wt:" + e.wt() + ")\t");
  63.             }
  64.             System.out.println();
  65.         }
  66.     }
  68.     // 返回图中一个顶点的所有邻边
  69.     // 由于java使用引用机制，返回一个Vector不会带来额外开销
  70.     @Override
  71.     public Iterable<Edge<E>> adj(int v) {
  72.         assert v >= 0 && v < n;
  73.         return g[v];
  74.     }
  75. }

最小生成树

最小生成树问题针对的是带权无向图，并且该图是一个连通图。

切分定理

1.切分

把图中的的顶点分成两部分，成为一个切分。

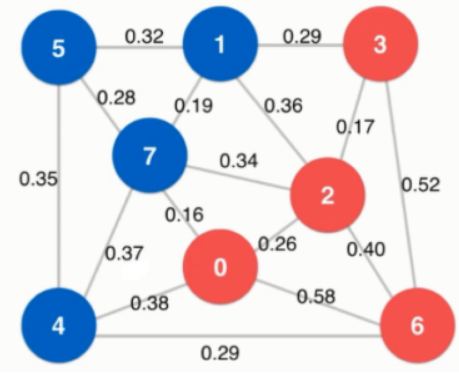
image.png

其中图中顶点被分为蓝色部分和红色部分，这就是一个切分。

2.横切边

如果一个边的两个端点，分别属于不同的切分，则这个边就被成为横切边

image.png

其中使用绿色标出了横切边。

3.切分定理

给定任意切分，横切边中权值最小边必然属于最小生成树

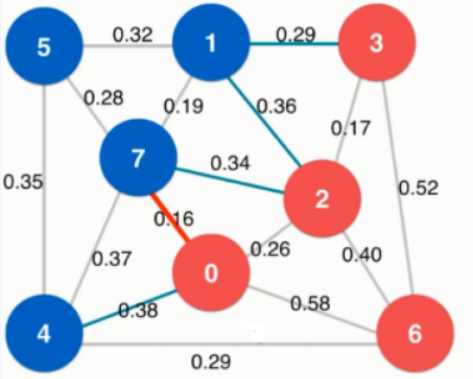
image.png

在这个切分中横切边中权值最小的是0.16，已使用红色标出。

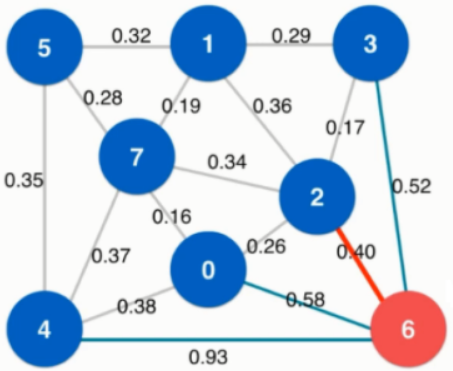
image.png

在这个切分中横切边中权值最小的是0.4，已使用红色标出。

Lazy Prim

  1. public class LazyPrimMST<E extends Number & Comparable> {
  2.     private WeightedGraph<E> G;    // 图的引用
  3.     private PriorityQueue<Edge<E>> pq;   // 最小堆, -->Java默认使用小根堆
  4.     private boolean[] marked;           // 标记数组, 在算法运行过程中标记节点i是否被访问
  5.     private Vector<Edge<E>> mst;   // 最小生成树所包含的所有边
  6.     private Number mstWeight;           // 最小生成树的权值
  8.     public LazyPrimMST(WeightedGraph graph){
  9.         this.G=graph;
  10.         pq=new PriorityQueue<>();
  11.         marked=new boolean[graph.V()];
  12.         mst=new Vector<>();
  14.         //从0节点开始访问
  15.         visit(0);
  16.         while(!pq.isEmpty()){
  17.             //获取最小边
  18.             Edge<E> e=pq.poll();
  19.             //看看这条最小边是否是横切边
  20.             if(marked[e.v()]==marked[e.w()]){
  21.                 continue;
  22.             }
  23.             //是横切边，说明就是MST的边
  24.             mst.add(e);
  26.             // 访问和这条边连接的还没有被访问过的节点
  27.             if(! marked[e.v()]){
  28.                 visit(e.v());
  29.             }else{
  30.                 visit(e.w());
  31.             }
  33.             //计算最小生成树的权值
  34.             mstWeight=mst.elementAt(0).wt();
  35.             for(int i=1;i<mst.size();i++){
  36.                 mstWeight = mstWeight.doubleValue() + mst.elementAt(i).wt().doubleValue();
  37.             }
  38.         }
  39.     }
  41.     //v顶点是未访问过的
  42.     private void visit(int v){
  43.         assert !marked[v];
  44.         marked[v]=true;
  45.         //将与v节点相连的顶点边加入到堆中
  46.         for(Edge e:G.adj(v)){
  47.             if(!marked[e.other(v)]){
  48.                 pq.add(e);
  49.             }
  50.         }
  51.     }
  53.     // 返回最小生成树的所有边
  54.     public Vector<Edge<E>> mstEdges(){
  55.         return mst;
  56.     }
  58.     // 返回最小生成树的权值
  59.     public Number result(){
  60.         return mstWeight;
  61.     }
  62. }

Prim 算法的优化

  1. /**
  2.  * 优化的Prim算法求图的最小生成树
  3.  */
  4. public class PrimMST<E extends Number & Comparable> {
  5.     private WeightedGraph G;              // 图的引用
  6.     private IndexMinHeap<E> ipq;     // 最小索引堆, 算法辅助数据结构
  7.     private Edge<E>[] edgeTo;        // 访问的点所对应的边, 算法辅助数据结构
  8.     private boolean[] marked;             // 标记数组, 在算法运行过程中标记节点i是否被访问
  9.     private Vector<Edge<E>> mst;     // 最小生成树所包含的所有边
  10.     private Number mstWeight;             // 最小生成树的权值
  12.     public PrimMST(WeightedGraph graph){
  13.         G = graph;
  14.         assert( graph.E() >= 1 );
  15.         ipq = new IndexMinHeap<E>(graph.V());
  17.         // 算法初始化
  18.         marked = new boolean[G.V()];
  19.         edgeTo = new Edge[G.V()];
  20.         mst=new Vector<>();
  22.         //Lazy Prim算法的改进
  23.         visit(0);
  24.         while (!ipq.isEmpty()){
  25.             // 使用最小索引堆找出已经访问的边中权值最小的边
  26.             // 最小索引堆中存储的是点的索引, 通过点的索引找到相对应的边
  27.             int v=ipq.extractMinIndex();
  28.             assert( edgeTo[v] != null );
  29.             mst.add(edgeTo[v]);
  30.             visit(v);
  31.         }
  33.         //计算最小生成树的权值
  34.         mstWeight=mst.elementAt(0).wt();
  35.         for(int i=1;i<mst.size();i++){
  36.             mstWeight=mstWeight.doubleValue()+mst.elementAt(i).wt().doubleValue();
  37.         }
  38.     }
  40.     private void visit(int v){
  41.         assert !marked[v];
  42.         marked[v] = true;
  44.         // 将和节点v相连接的未访问的另一端点, 和与之相连接的边, 放入最小堆中
  45.         for(Object edge:G.adj(v)){
  46.             Edge<E> e=(Edge<E>)edge;
  47.             int w=e.other(v);
  48.             // 如果边的另一端点未被访问
  49.             if(!marked[w]){
  50.                 if(edgeTo[w]==null){
  51.                     //如果从没有考虑过这个端点, 直接将这个端点和与之相连接的边加入索引堆
  52.                     //edgeTo[w] 表示访问w定点所对应的边<v,w>
  53.                     edgeTo[w]=e;
  54.                     ipq.insert(w,e.wt());
  55.                 }else if(e.wt().compareTo(edgeTo[w].wt())<0){
  56.                     //如果曾经考虑这个端点, 但现在的边比之前考虑的边更短, 则进行替换
  57.                     edgeTo[w]=e;
  58.                     ipq.change(w,e.wt());
  59.                 }
  60.             }
  61.         }
  62.     }
  64.     // 返回最小生成树的所有边
  65.     Vector<Edge<E>> mstEdges(){
  66.         return mst;
  67.     }
  69.     // 返回最小生成树的权值
  70.     Number result(){
  71.         return mstWeight;
  72.     }
  73. }

Kruskal

  1. public class KruskalMST<E extends Number & Comparable> {
  2.     private Vector<Edge<E>> mst;   // 最小生成树所包含的所有边
  3.     private Number mstWeight;           // 最小生成树的权值
  5.     public KruskalMST(WeightedGraph graph){
  6.         mst=new Vector<>();
  8.         // 将图中的所有边存放到一个最小堆中
  9.         PriorityQueue<Edge<E>> pq=new PriorityQueue<>(graph.E());
  10.         for(int i=0;i<graph.V();i++){
  11.            for(Object item:graph.adj(i)){
  12.                Edge<E> e=(Edge<E>)item;
  13.                if(e.w() <e.v()){ //由于是无向图，只要加入一条边就好了
  14.                    pq.add(e);
  15.                }
  16.            }
  17.         }
  19.         //创建一个并查集, 来查看已经访问的节点的联通情况
  20.         UnionFind uf = new UnionFind(graph.V());
  21.         while (!pq.isEmpty() && mst.size()<graph.V()-1){
  22.             // 从最小堆中依次从小到大取出所有的边
  23.             Edge<E> e = pq.poll();
  25.             //如果该边的两个端点是联通的, 说明加入这条边将产生环, 扔掉这条边
  26.             if(uf.isConnected(e.w(),e.v())){
  27.                 continue;
  28.             }
  30.             // 否则, 将这条边添加进最小生成树, 同时标记边的两个端点联通
  31.             mst.add(e);
  32.             uf.unionElements(e.w(),e.v());
  33.         }
  35.         // 计算最小生成树的权值
  36.         mstWeight = mst.elementAt(0).wt();
  37.         for( int i = 1 ; i < mst.size() ; i ++ ){
  38.             mstWeight = mstWeight.doubleValue() + mst.elementAt(i).wt().doubleValue();
  39.         }
  40.     }
  42.     // 返回最小生成树的所有边
  43.     Vector<Edge<E>> mstEdges(){
  44.         return mst;
  45.     }
  47.     // 返回最小生成树的权值
  48.     Number result(){
  49.         return mstWeight;
  50.     }
  51. }

时间复杂度

算法 时间复杂度
Lazy Prim O(ElogE)
Prim O(ElogV)
Kruskal O(ElogE)