红黑树

什么是红黑树

2-3树

• 性质：

1. 满足二叉搜索树的基本性质
2. 节点可以存放一个或者两个元素，存放一个元素的节点成为2节点，存放两个元素的节点成为3节点。

1. 2-3树是一棵绝对平衡的树，即从根节点到任意一个叶子节点所经过的节点数都相同

• 下图是一棵完整的2-3树：

2-3树是如何维持绝对平衡的

向2-3树中添加节点的操作如下：

对于2-3树来说，每次添加节点永远不会添加到一个空的位置！

• 向2-节点中插入数据6，6和12融合形成一个3节点：

• 向3-节点中插入数据2，先融合暂时形成一个4节点，再分裂：

• 向3-节点中插入数据4，并且该3-节点父节点是2-节点，3节点先融合暂时形成一个4节点，再分裂，接着与父节点进行融合：

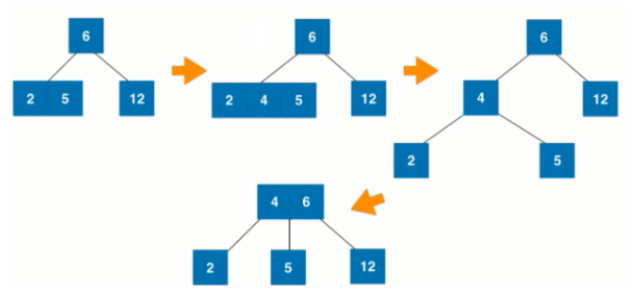
• 向3-节点中插入数据4，并且该3-节点父节点也是3-节点，该3节点先融合暂时形成一个4节点，再分裂，接着与父节点进行融合暂时形成一个4节点，这个4节点再分裂：

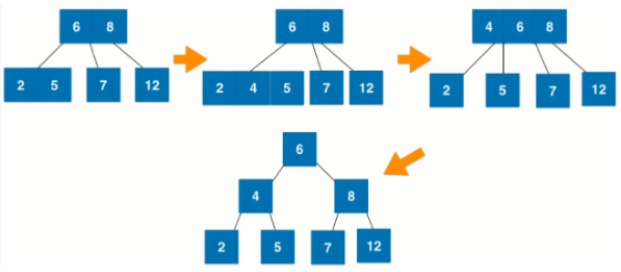
红黑树和2-3树

红黑树本质上其实等价于2-3树，2-3树中2-节点等同于红黑树中的“黑”节点，2-3树中的3-节点等同于红黑树中的“红”节点+红边+“黑”节点。

其中红节点表示和父节点是是一种并列的关系，由于在树的实现过程是一个二叉树，即每个节点最多只能存储一个元素，红节点的引入是为了表示2-3树的3节点的一种实现方式。在所有的红黑树中，所有的红节点一定是向左倾斜的。

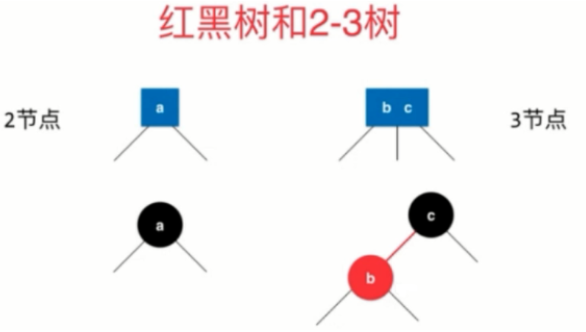
基于红黑树和2-3树的关系，我们可以将2-3树转化为红黑树：

即

红黑树性质

1. 每个节点或者是红色的，或者是黑色的
2. 根节点是黑色的

3. 每一个叶子节点(最后的空节点)是黑色的

   这其实是一个定义

4. 如果一个节点是红色的，那么它们的孩子节点都是黑色的

   因为红节点和其父亲节点表示一个3节点，黑色节点的右孩子一定是黑色节点。

5. 从任意一个节点到叶子节点经过的黑色节点都是一样的

   因为2-3树是绝对平衡的

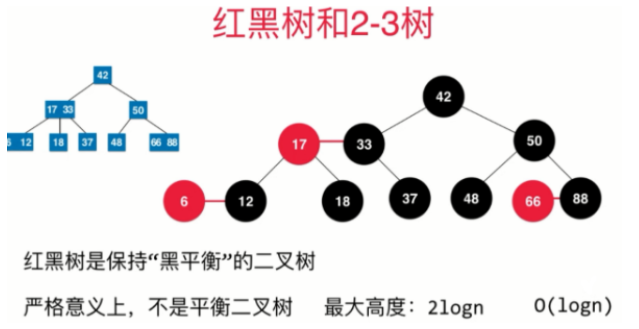
相较于AVL树，红黑树上的查找的操作的效率的低于AVL树的。但对于增删操作，红黑树的性能是更优的。

添加新元素

节点的默认颜色设置为红色，因为添加新元素的时候，默认先是与一个节点进行融合的。

public class RBTree<K extends Comparable<K>,V>{
    private static final boolean RED=true;
    private static final boolean BLACK=false;
    private class Node{
        public K key;
        public V value;
        public Node left,right;
        public boolean color;
        public Node(K key,V value){
            this.key=key;
            this.value=value;
            this.left=null;
            this.right=null;
            //2-3树中添加一个新元素
            //元素添加进2-节点，会形成3-节点
            //元素添加进3-节点，会先形成4-节点，然后进行相应的转换
            //因为2-3树添加新元素的时候，永远不会将其放置到空位置上
            //而是默认与一个节点融合，所以节点的默认颜色设置为红色
            this.color=RED;
        }
    }
}

保持根节点为黑色

//判断节点是否是红色
private boolean isRed(Node node){
    if(node==null){
        return BLACK;
    }
    return node.color;
}
public void add(K key, V value) {
    root=add(root,key,value);
    //红黑树性质： 2.根节点是黑色的
    root.color=BLACK;
}

左旋转

对以node为根节点的如下子树进行左旋转：

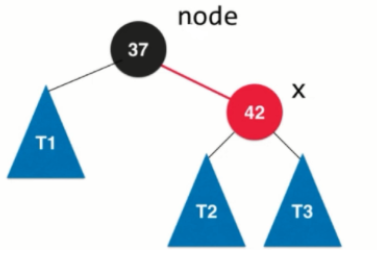
1. 首先进行节点的左旋转

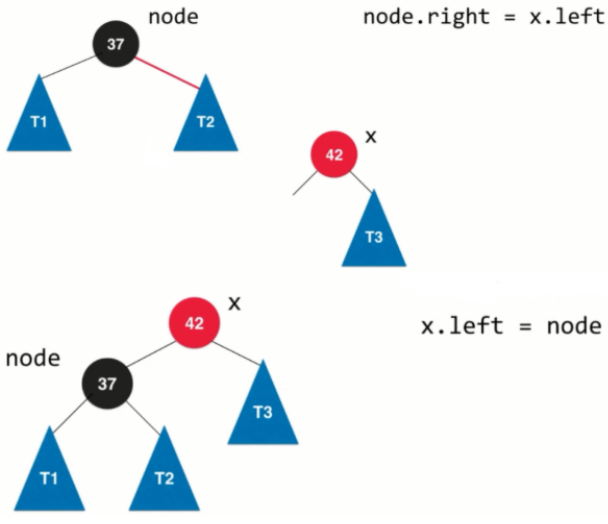
1. 再进行颜色的翻转

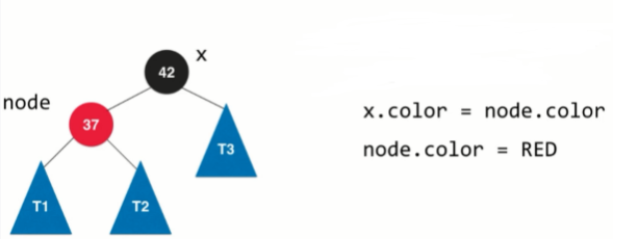
//左旋转
//   node                     x
//  /   \     左旋转         /  \
// T1   x   --------->   node   T3
//     / \              /   \
//    T2 T3            T1   T2
private Node leftRotate(Node node){
    Node x=node.right;
    //左旋转
    node.right=x.left;
    x.left=node;
    //改变节点颜色
    x.color=node.color;
    node.color=RED;
    return x;
}

右旋转

右旋转和左旋转同理

1. 首先进行右旋转

1. 再进行颜色的翻转

//右旋转
//     node                   x
//    /   \     右旋转       /  \
//   x    T2   ------->   y   node
//  / \                       /  \
// y  T1                     T1  T2
private Node rightRotate(Node node) {
    Node x=node.left;
    //右旋转
    node.left=x.right;
    x.right=node;
    x.color=node.color;
    node.color=RED;
    return x;
}

颜色翻转

2-3树中3-节点插入66：

对应的红黑树中：

此时可以将这三个节点就是2-3树中的4-节点，这时就需要颜色翻转：

注：44转换为红色，方便后续的操作，(与其他的节点“融合”)

//颜色翻转
private void flipColors(Node node){
    node.color=RED;
    node.left.color=BLACK;
    node.right.color=BLACK;
}

添加新元素

红黑树添加新元素的过程可以概括为下面一个过程：

public void add(K key, V value) {
    root=add(root,key,value);
    //红黑树性质： 2.根节点是黑色的
    root.color=BLACK;
}
private Node add(Node node,K key,V value){
    if(node==null){
        size++;
        return new Node(key,value);
    }
    if(key.compareTo(node.key)<0){
        node.left=add(node.left,key,value);
    }else if(key.compareTo(node.key)>0){
        node.right=add(node.right,key,value);
    }else{
        node.value=value;
    }
    //    黑
    //    /
    //   红
    //    \
    //    红
    //左旋转
    if(isRed(node.right) && !isRed(node.left)){
        node=leftRotate(node);
    }
    //    黑
    //    /
    //   红
    //   /
    // 红
    //右旋转
    if(isRed(node.left) && isRed(node.left.left)){
        node=rightRotate(node);
    }
    //     黑
    //    /  \
    //   红   红
    // 颜色翻转
    if(isRed(node.left) && isRed(node.right)){
        flipColors(node);
    }
    return node;
}

红黑树性能总结

• 对于完全随机的数据，建议使用普通的BST。但是在极端情况下，会退化成链表！(或者高度不平衡)
• 对于查询较多的使用情况，建议使用AVL树。
• 红黑树牺牲了平衡性(2log n的高度)，统计性能更优(增删改查所有的操作)