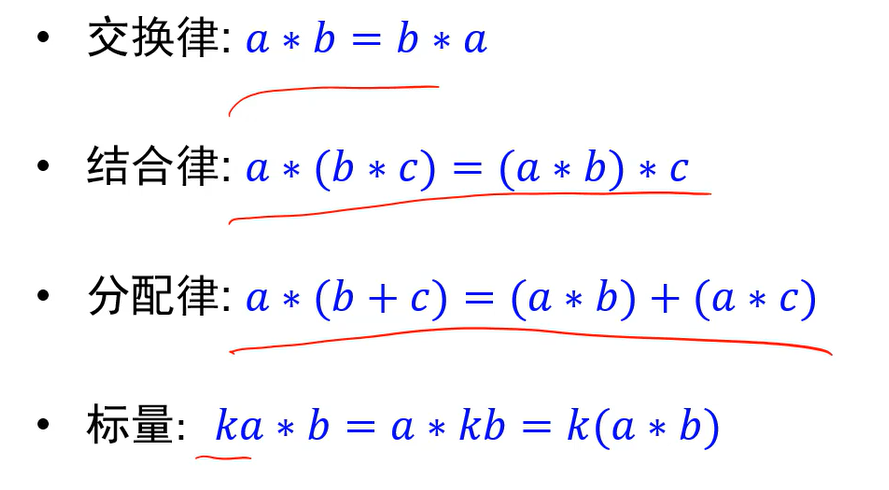07 卷积&图像去噪&边缘提取
补充材料1:卷积与图像去噪
图像去噪
- 噪声图像通常是,一个点和周围的点差别比较大,让人感觉起来比较突兀。
- 去除噪声一种最直接的思想就是把这个点和周围的点平均一下,来靠近周围的点。
- 最简单的就是和周围的点加权求和,这个过程就是对图像中的一个像素点进行的卷积操作。
- 图像中每一个点都进行这个卷积操作,就得到一张新的图像,这就是对图像的卷积。
- 加权的权值我们通常会存到一个模板里面,称之为卷积核/滤波核。

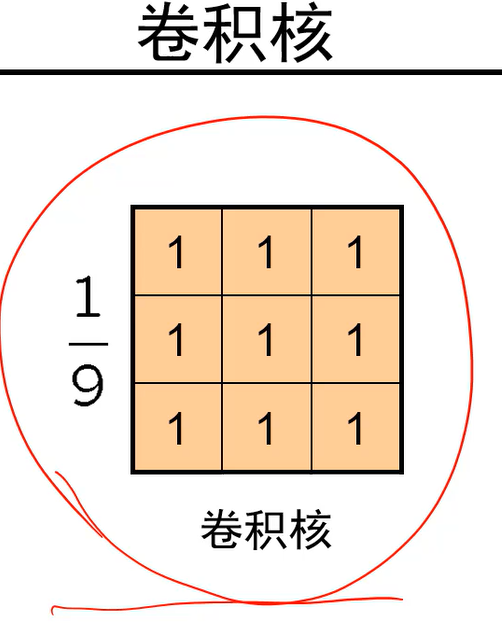
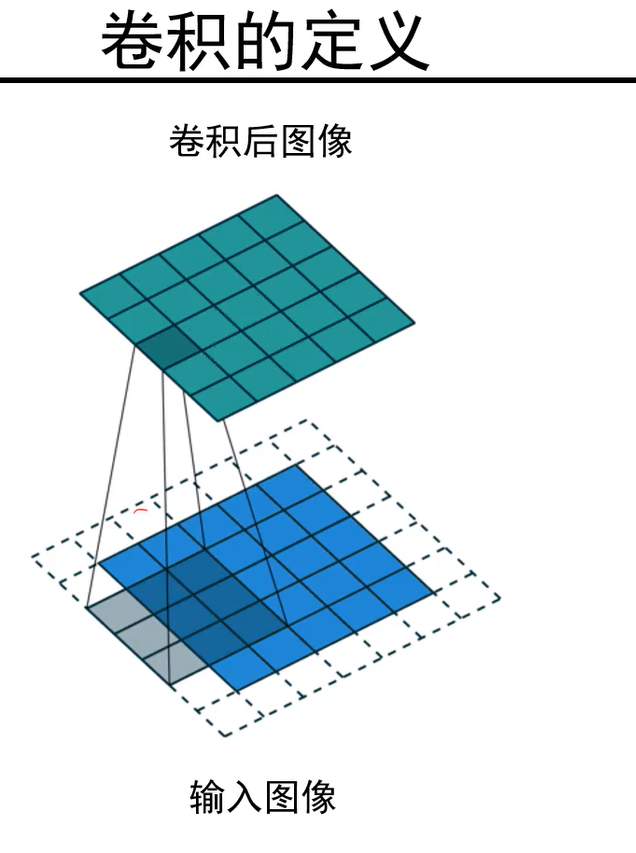
具体做的时候,就是图像3*3区域上都有一个卷积核,把卷积核罩住的元素进行对应位置相乘(即乘权值)并累加,就得到处理后的点,图像每个点都处理后就会得到一张新图像。
卷积的定义
卷积的性质
叠加性:两个图像求和以后卷积等于两个图像分别卷积后求和。
- 平移不变性:对一个信号平移后再卷积,等于卷积后再平移。因为对于3*3的模板,卷积只依赖周围8个值,平移后,只要周围8个值不破坏,结果是一样的。
- 另外,所有平移操作都可以用卷积来实现。

- 更多性质:
小结
边界填充
卷积操作有个很令人头疼的问题,就是边界上的问题,在边界上卷积会遇到无像素区域。
因此要进行真实的计算,保证卷积前后的图像一样大小的话,就要进行边界填充。
- 如果不考虑边界填充,那么输出的图像会小一圈。

- 我们不希望这样,因此会对边界进行填充,比如都填充成0(zero padding)
- 填充完再去卷积,结果就和原图大小一样了。
- 除了零填充,还有拉伸和镜像。
 :::info
还有其他填充方式,深度学习更常用的是零填充,来保证输入输出图像一样大。
:::
:::info
还有其他填充方式,深度学习更常用的是零填充,来保证输入输出图像一样大。
:::
小结
- 卷积操作后的图像要小于输入时图像,通过边界填充问题,我们可以实现卷积前后图像的尺寸不变。
-
卷积示例
模板有个参数是模板的尺寸,作用就是指定要和周围多少个像素进行平均。

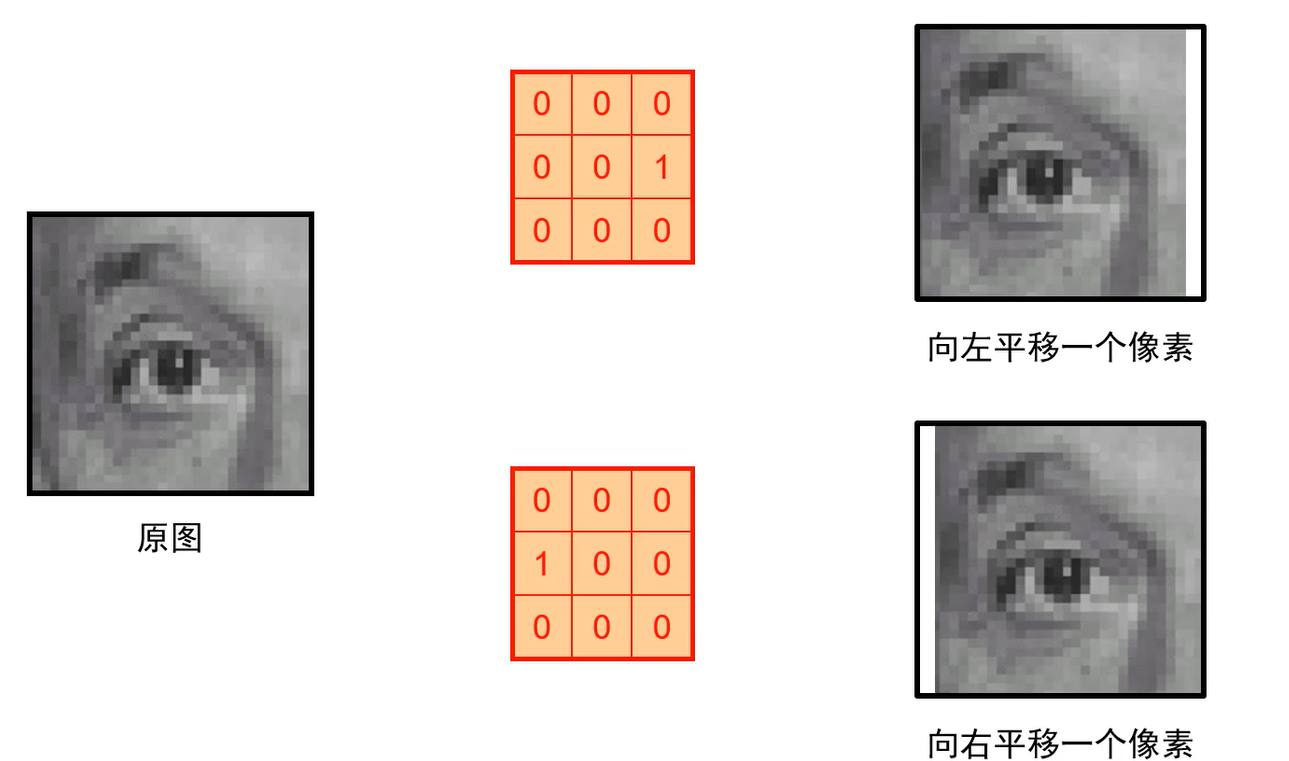
由上图可以看出,任何平移操作都可以用卷积来实现。
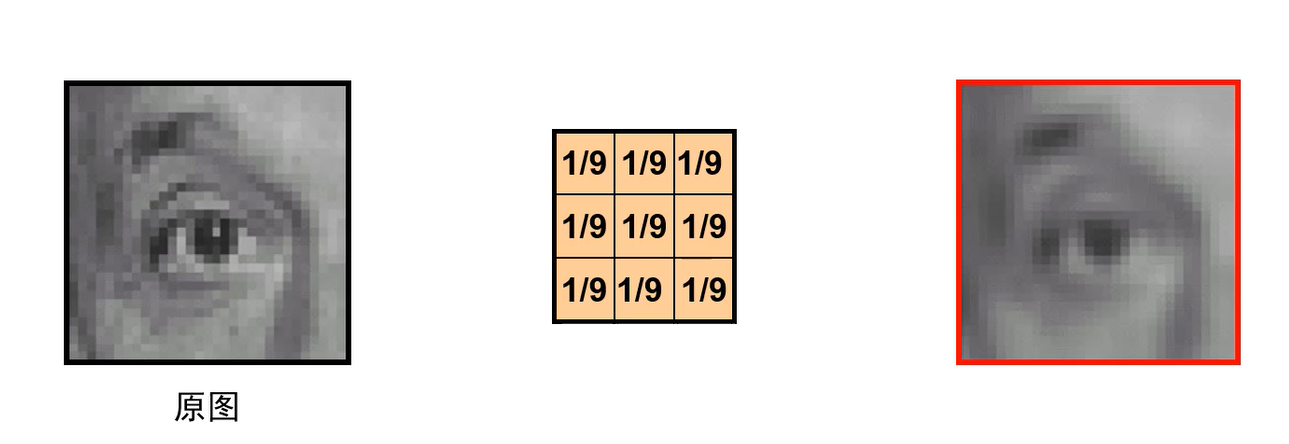
- 上面模板起的作用是和周围像素进行平均,能够起到边缘平滑的作用。
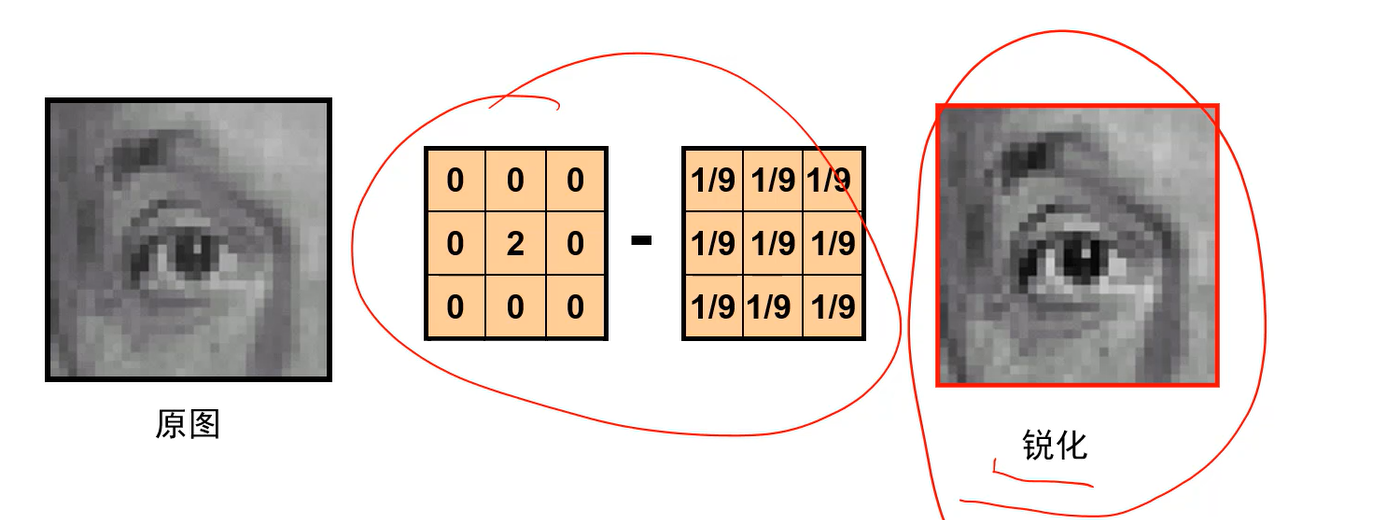
- 这个模板为何能锐化呢?
Q:原图减去平滑后的图会得到什么? A:如果原图全是255,一个点周围也都是255,平滑后不会发生改变,两者相减会都变为0。 但是如果原图有一条边,左边是255,右边是0,那么这个地方平滑后会变成128,这个值改变之前在原图上是很尖锐的255,平滑后变为128;此时原图和平滑图两者相减就会产生很大的值。 因此原图减去平滑后的图剩下的就是边缘图。
原图减去平滑后的图剩下的会是边缘图。将边缘图加回原图里,则细节信息就更丰富了,这样就得到的锐化的结果。

- 这样就看懂了操作的过程,从这个角度看,模板和原始信号卷积的时候,有些模板可以让原图什么都不改,有些模板可以让原图平移,有些模板可以让图像有磨皮的效果,反过来有些模板可以让图像进行增强,这就是卷积的魅力。
- 卷积是个很基础的操作,可以让我们实现很多图像处理效果。
小结

高斯卷积核
- 平均卷积核存在的问题:振铃。
- 产生原因:模板是方形模板,所有的权值都是一样的。
- 解决方法:根据邻域像素与中心的远近程度分配权重。就能有效的解决振铃问题。

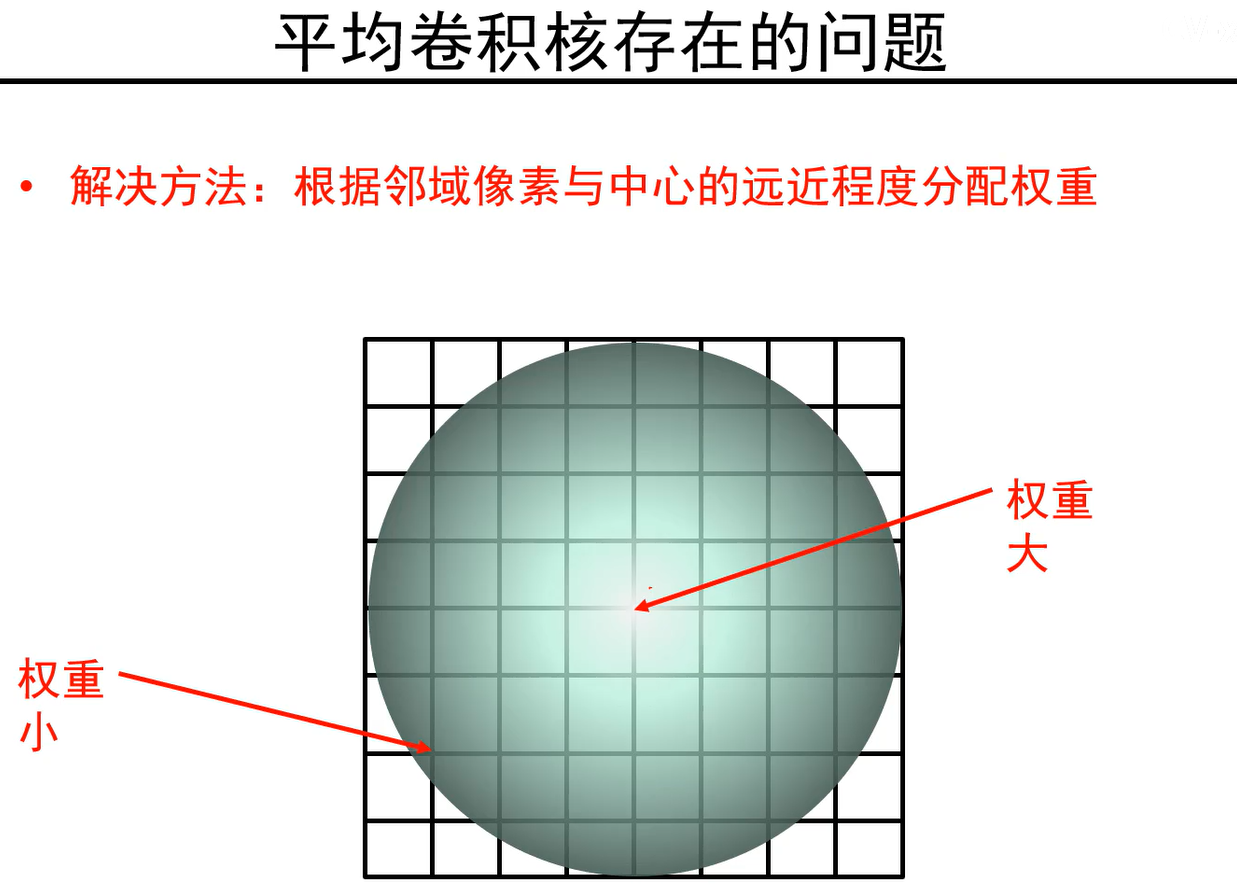
- 而使用高斯卷积核就能产生这种模板,中间最大大,越往边上越小。
- 生成步骤:
- 1、确定卷积核的尺寸,比如
- 2、设置高斯函数的标准差,比如
- 3、计算卷积核各个位置的权重,如G(0, 0), G(0, 1)
- 4、对权重值进行归一化(即要整个模板加起来为1)
- 如果不归一化,如果卷积核总和小于1,就会将卷积前的结果衰减;如果总和超过1,就会把像素值放大。
- 只有总和是1时才表示我和我周边的点加起来不会改变像素范围,不会对信号衰减或增强。


平滑模板要求对权重进行归一化。即卷积核的权重总和为1.
- 如何设置下述参数:
- 1、卷积核的尺寸
- 2、高斯函数的标准差
- 设置参数之前,首先了解这两个参数分别有什么作用。
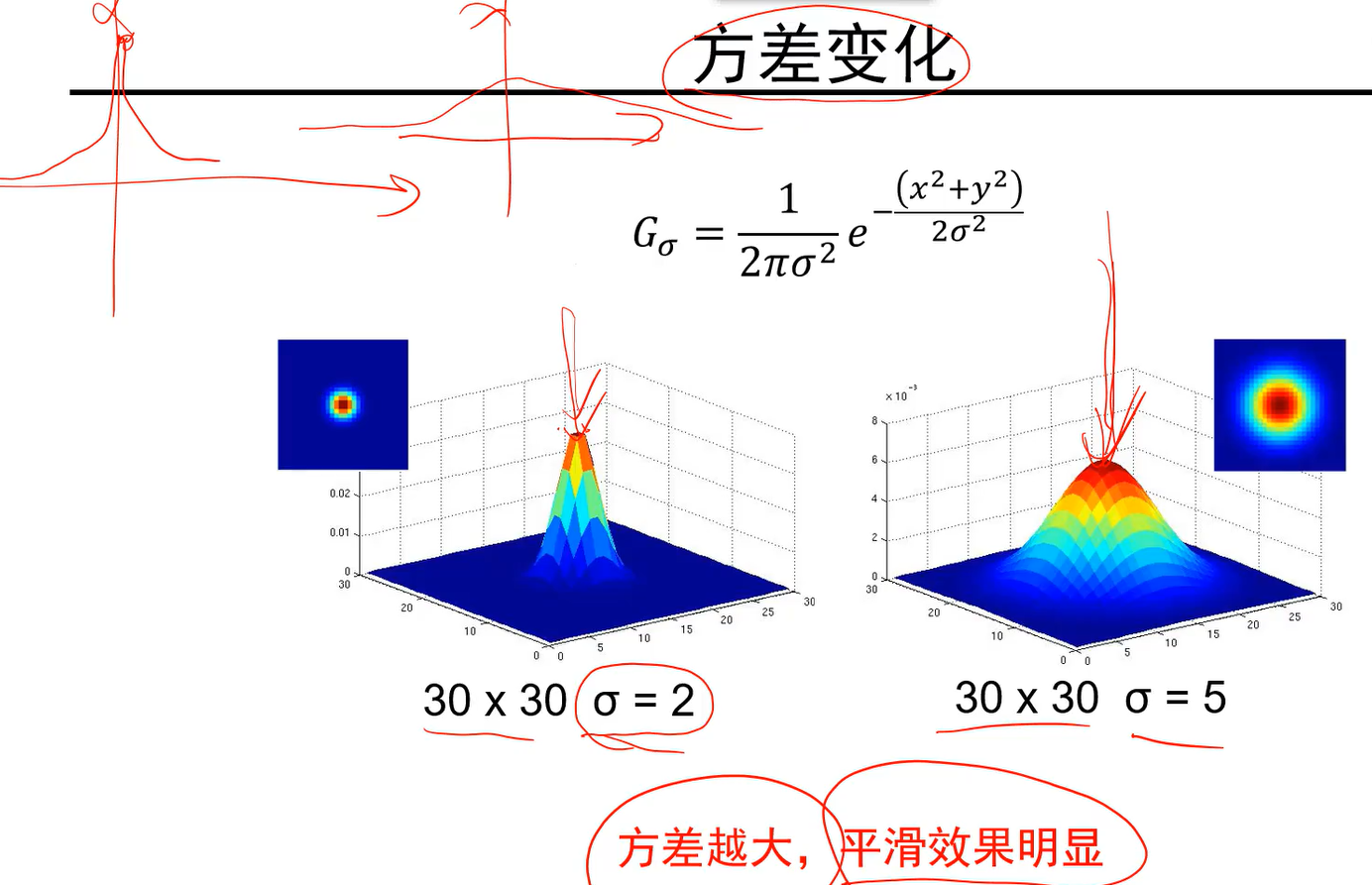
- 方差变化:
- 下图中,方差为2的,中间位置的权重值大,因此和周边邻居加权后,被平滑的就没那么厉害;相反,方差大时,由于中间点自身的权重小,在最后总结果里占的权重小,则最后被改变的可能性就比较大,就比较容易受到周边像素的影响,卷积后平滑的就越厉害。
- 因此,方差越大,平滑的就越明显。
- 窗宽变化:
- 方差不变了,理论上中间两个点的高斯输出是一样的。然而,由于最后要经过权值归一化,模板尺寸大时,作为分母的项就越多,比如下图左边是100个元素求和,右边是900个元素求和。
- 因此小窗口,由于分母小,则中间的值要大一点; 大窗口,由于分母大,则中间的值要小一点;因为中间的值越大,平滑能力越弱。
- 因此模板尺寸越大,平滑效果越强。
总结

由正态分布图像,正负
之外,高斯的值接近于0,就没有什么意义了。
高斯卷积核的结果 vs 平均卷积核
高斯卷积核的特性
去除图像中的“高频”成分(低通滤波器)
- 高斯卷积核还是把自己和周围加权,加权后自身就会向周围靠拢一些,如果这个点很突兀,和周围平均就会减弱一些,就会滤除图像中的高频信息(即和周围差异比较大的信息如噪声,边缘)。
- 两个高斯卷积核卷积后得到的还是高斯卷积核
- 连续两次小方差卷积,等价于一次大方差卷积。这在卷积神经网络中很有启发,后面会讲到。
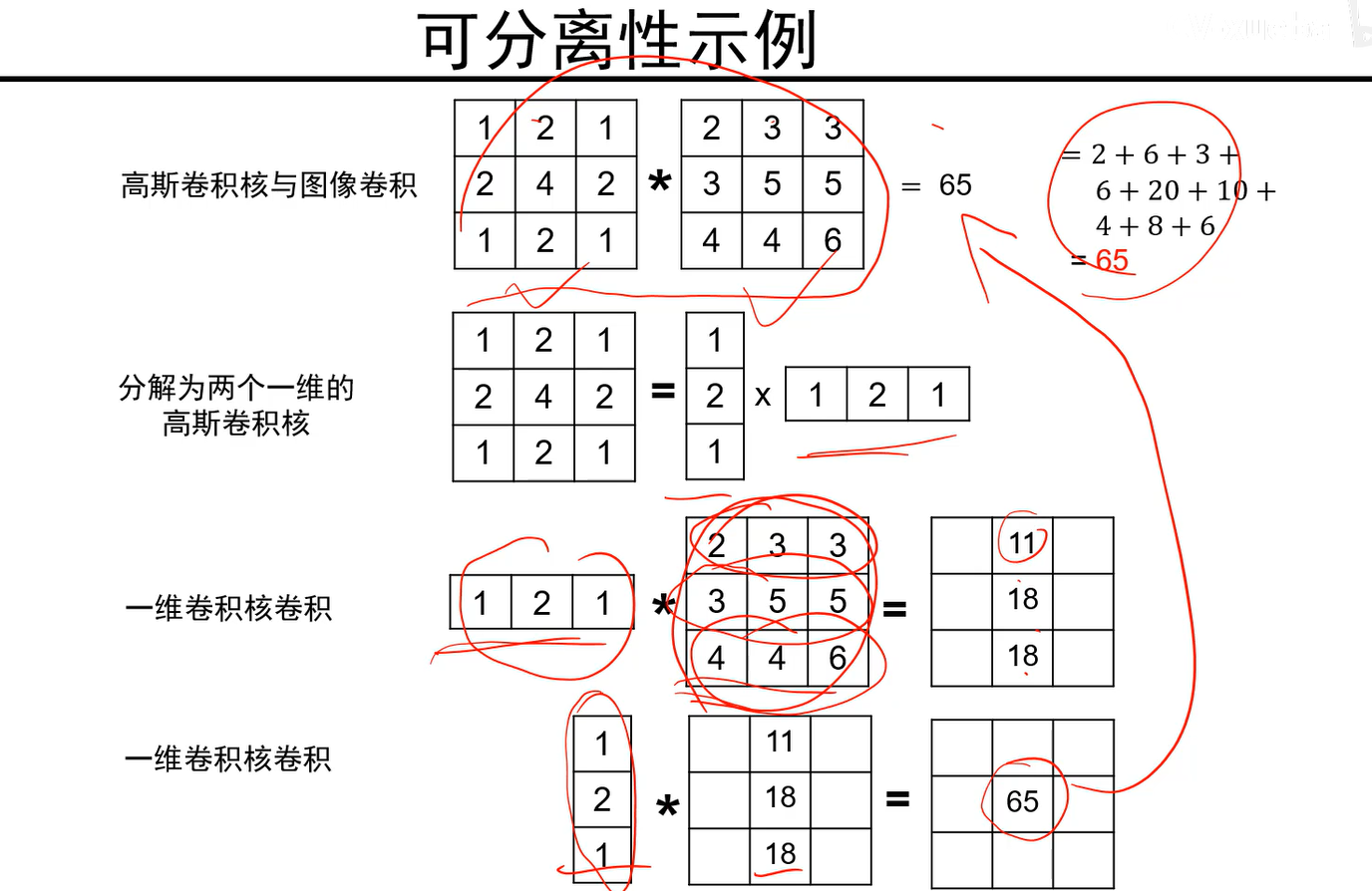
- 可分离
- 一个二维高斯核可以分解为两个一维高斯的乘积。

图像噪声与中值滤波器
我们上面介绍了去噪,但还没对噪声进行介绍。然后介绍另一个滤波操作,中值滤波操作。
噪声
- 椒盐噪声
- 脉冲噪声
- 高斯噪声
高斯噪声
- 相当于原图每个像素的理想图加上一个噪声项,我们认为噪声项服从正态分布,通常
=0,
很小。
- 高斯噪声是逐点产生的,每个点上都叠加一个噪声分布中随机采样的值,和真实的值一叠加就得到了所看到的。
减少高斯噪声

- 原来是一张很均匀的灰图,上面的像素都是128。经过方差等于0.05, 0.1, 0.2加噪声污染后得到的图如第一行所示。
- 接下来第二行的方差是高斯模板的方差,模板的窗宽在每一行的左侧。用这两个模板去滤波, 可以看到在噪声的方差为0.02较小时,方差为2的模板就能将原图恢复出来;而噪声方差为0.2时,并没有将原图恢复出来。
- 因此噪声的方差越大,卷积核的方差也要越大,这就是高斯去噪。
- 因为方差越大,对图的平滑也越厉害,在去除噪声的同时,图片也受到影响(比如第三张人像虽然去除了噪声,但比第一张看上去要糊)
结论:高斯噪声较大时,就要用大方差的卷积模板,但也会带来副作用,即有用的信号也会被平滑。
椒盐噪声
中值滤波
- 中值滤波器也是个33或55,7*7的模板,但模板是空的,没有权重。
- 具体计算时,将模板套到相应区域时将里面的值排序,将排序后的中值取出来,去替换原来的点。
- 这种滤波的好处:滤波后的值一定是原图像上某个像素值,而不是产生的。
小结

- 高斯滤波是加权求和操作,因此将这种滤波称为线性滤波器。
- 而中值滤波是排序取中值,不是线性滤波器。
补充材料2:卷积与边缘提取
- 边缘:图像中亮度明显而急剧变化的点
- 为什么要研究边缘:
- 编码图像中的语义与形状信息
- 想对于像素表示,边缘表示显然更加紧凑,如右图。
边缘的种类
- 深度不连续:真实情况下并不存在,是因为拍照而显示出来的。
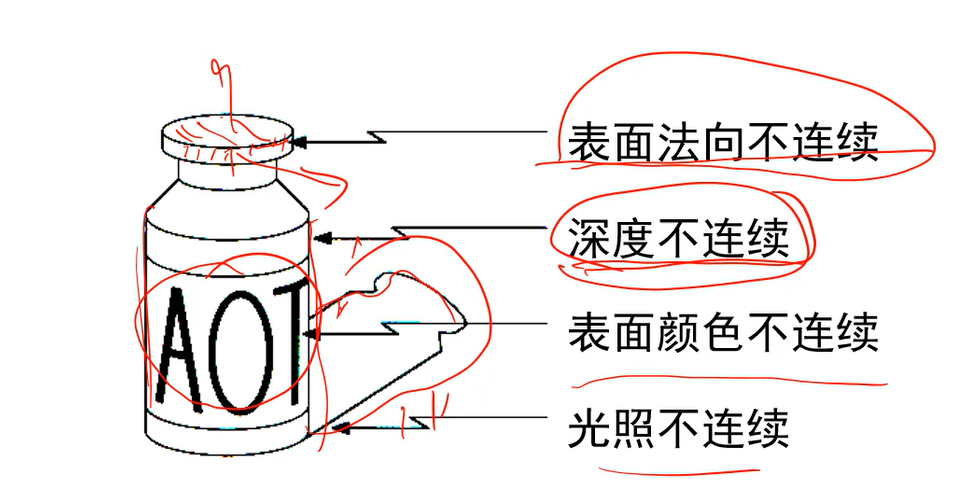
Q:为什么要了解边的类型?
A:因为不同的任务研究不同的边。比如,如果要研究瓶子里装的东西,则AOT三个字母有意义,其他边对于我理解瓶子里装什么没有任何意义;如果要看瓶子是否在桌子上,我们可能就要来看阴影的边。
边缘检测
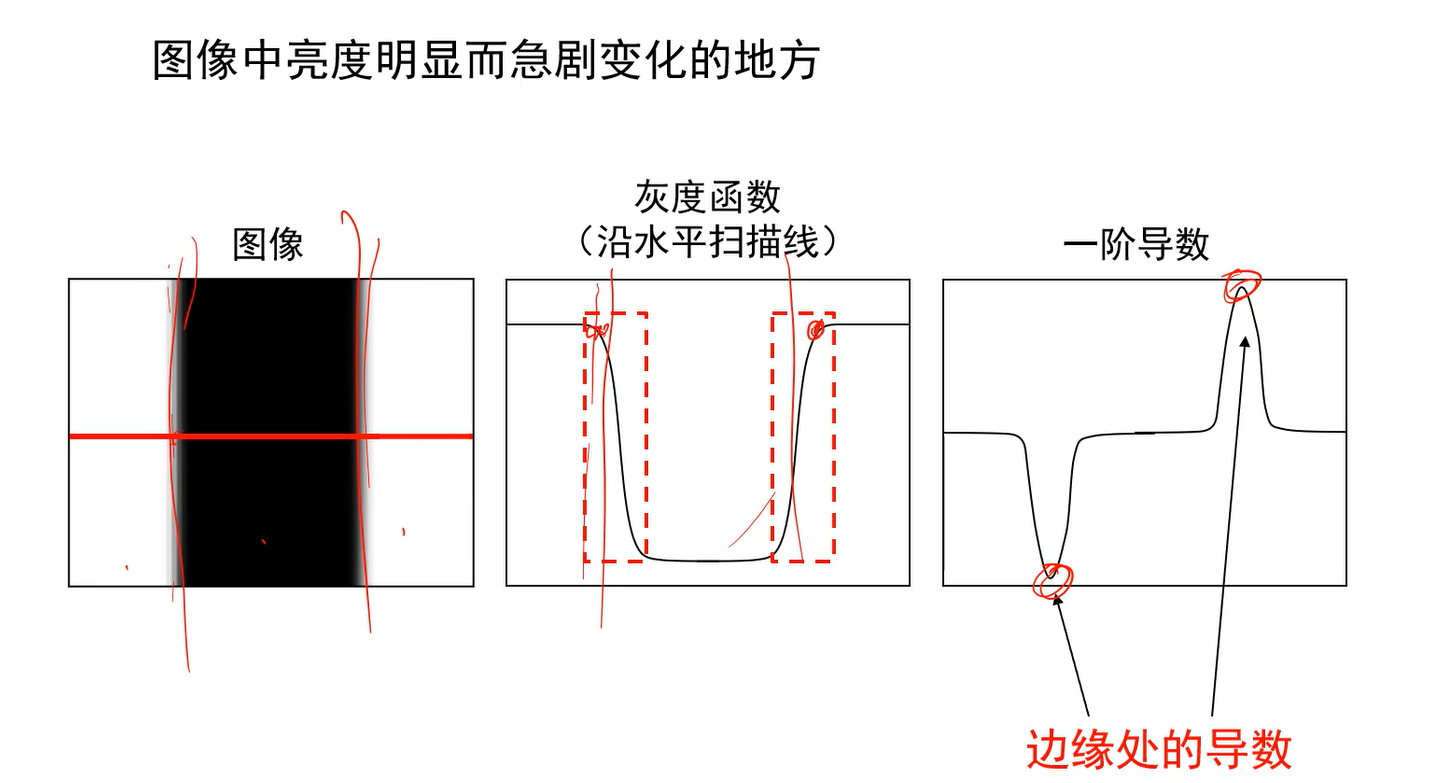
- 怎么检测出图中一维信号的边呢?在数学中,信号急剧变化最大的点即导数变化最大的点。
- 因此用图像的导数来检测边缘,对信号进行求导即可。
图像求导

图像求导不想那么复杂,直接取简化,如图所示:
由图像求导公式看出,右边像素减去自己即自己的导数,而右边像素减去自己这件事情可以用卷积核来实现。
- 对图像求导后如下图:
- 左图为对x求偏导。看到的边是y方向的,对于y方向的边,只有左边右边有区别,上下没有区别,因此x方向求导求出的是y方向的边。
- 同理y方向求导求出的是x方向的边。
图像梯度
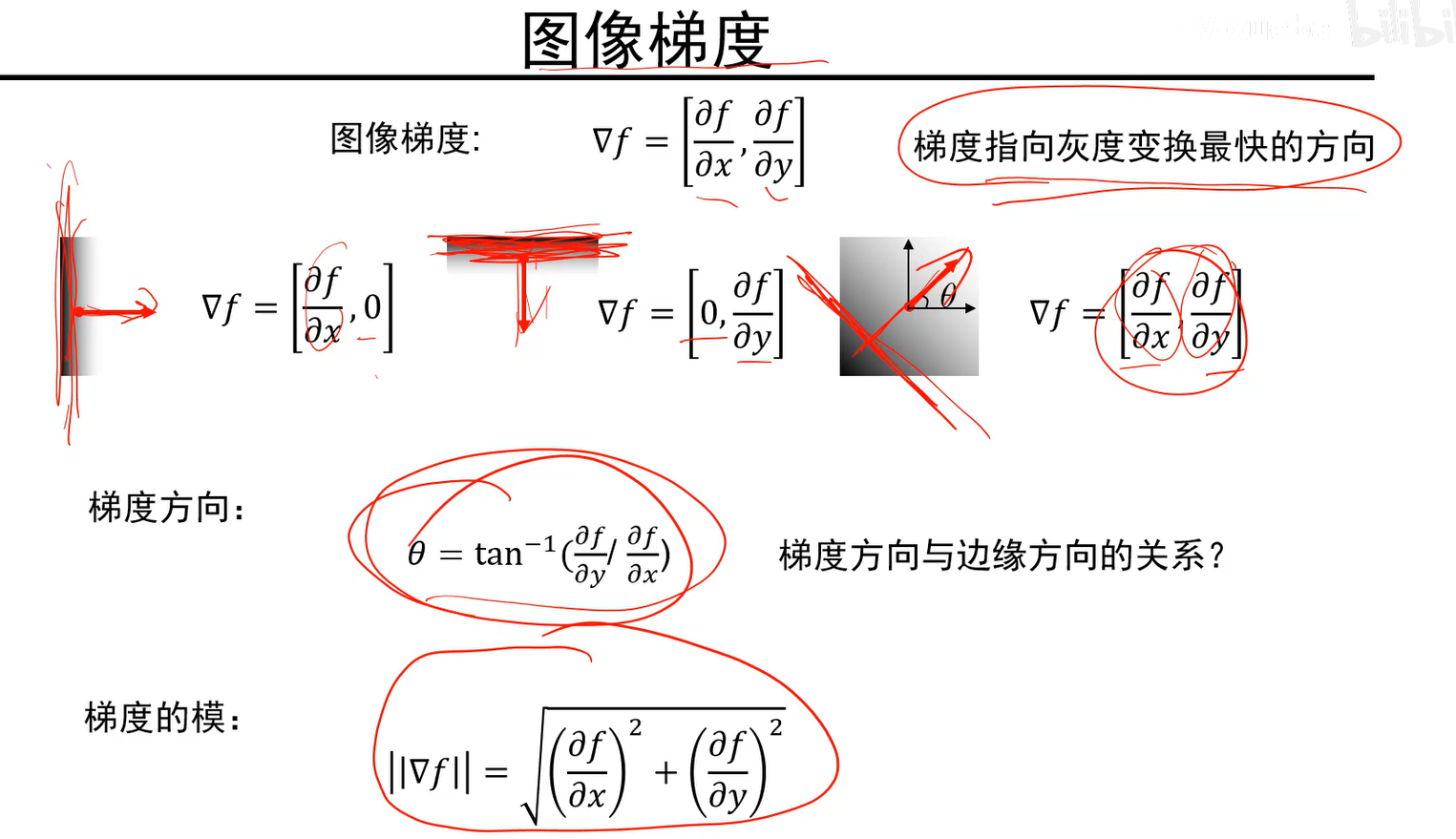
- 两个方向的导数组成的向量即图像的梯度。
- 梯度方向还可以让我们知道信号的朝向,梯度方向和信号朝向是垂直的。
- 图像梯度通常是从暗的地方指向亮的地方,即灰度方向变化最快快的方向。
- 梯度的模值越大,表示当前点是边缘的可能性越大。
- 如下图,最右边是梯度模值图像,可以看出近似是图像的边缘了。
- 因此可用模值来反映图像的边缘信息。
噪声的影响
通常信号是有噪声的,如果直接求导,会得到下图下面的结果,这样用导数最大值就无法找到边缘。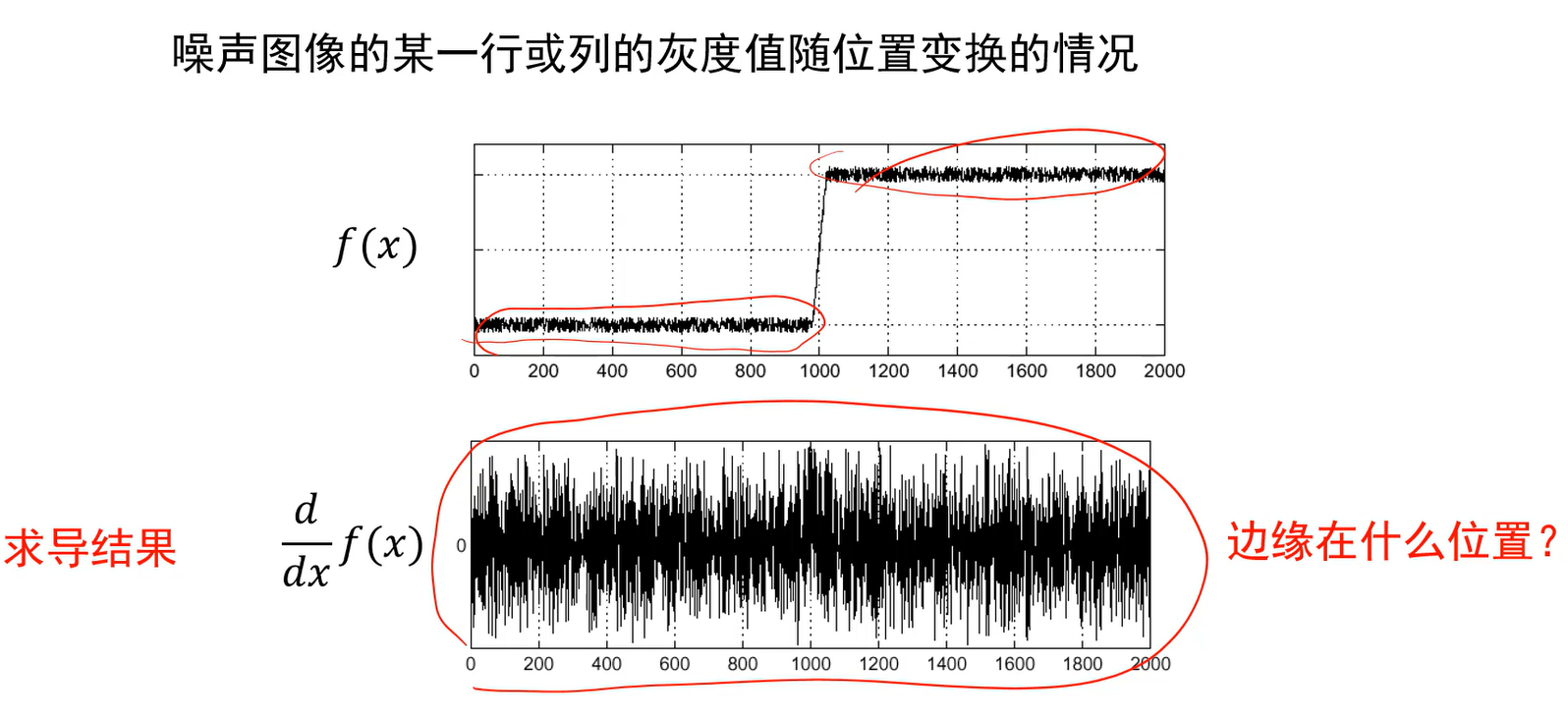
解决方法:先平滑
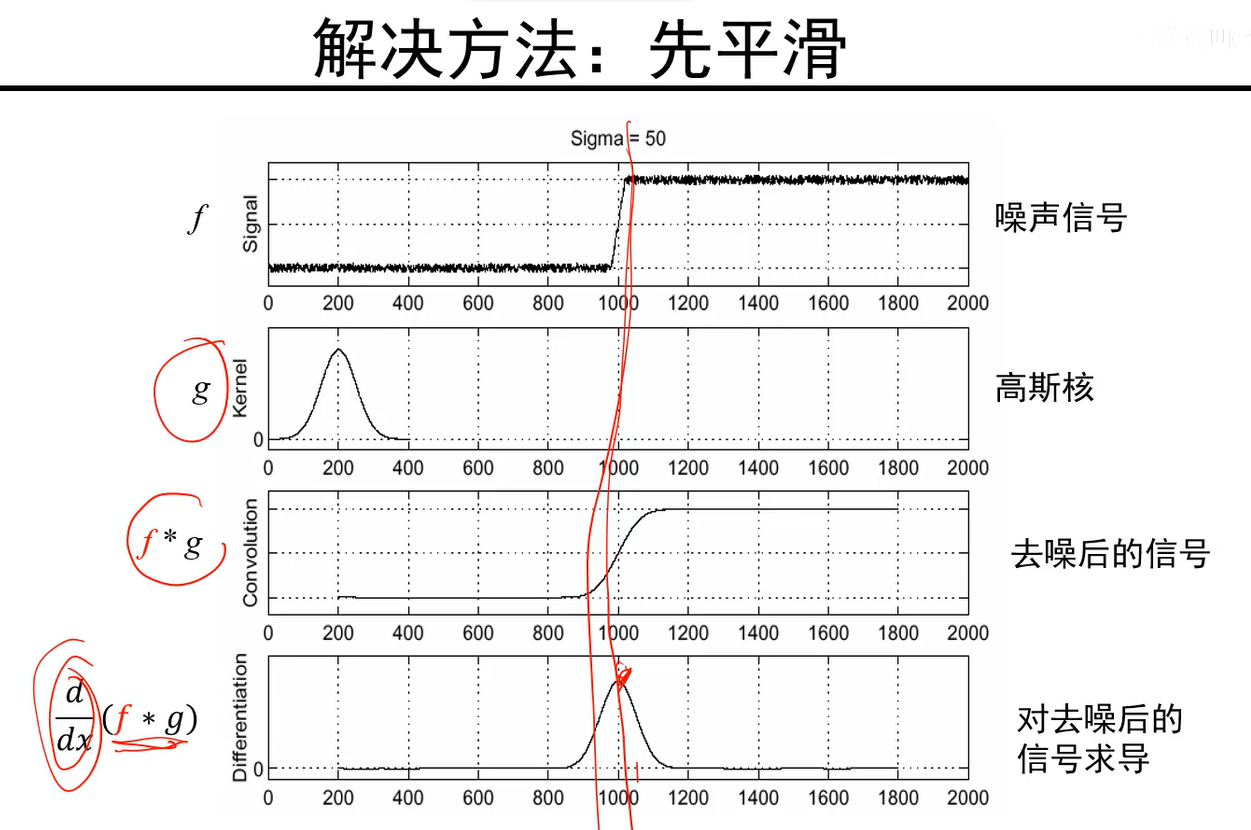
可以看出上图每个点都有噪声,因此可以确定为高斯噪声,因此先用高斯核进行平滑,平滑后再去求导就能找到边缘位置了。
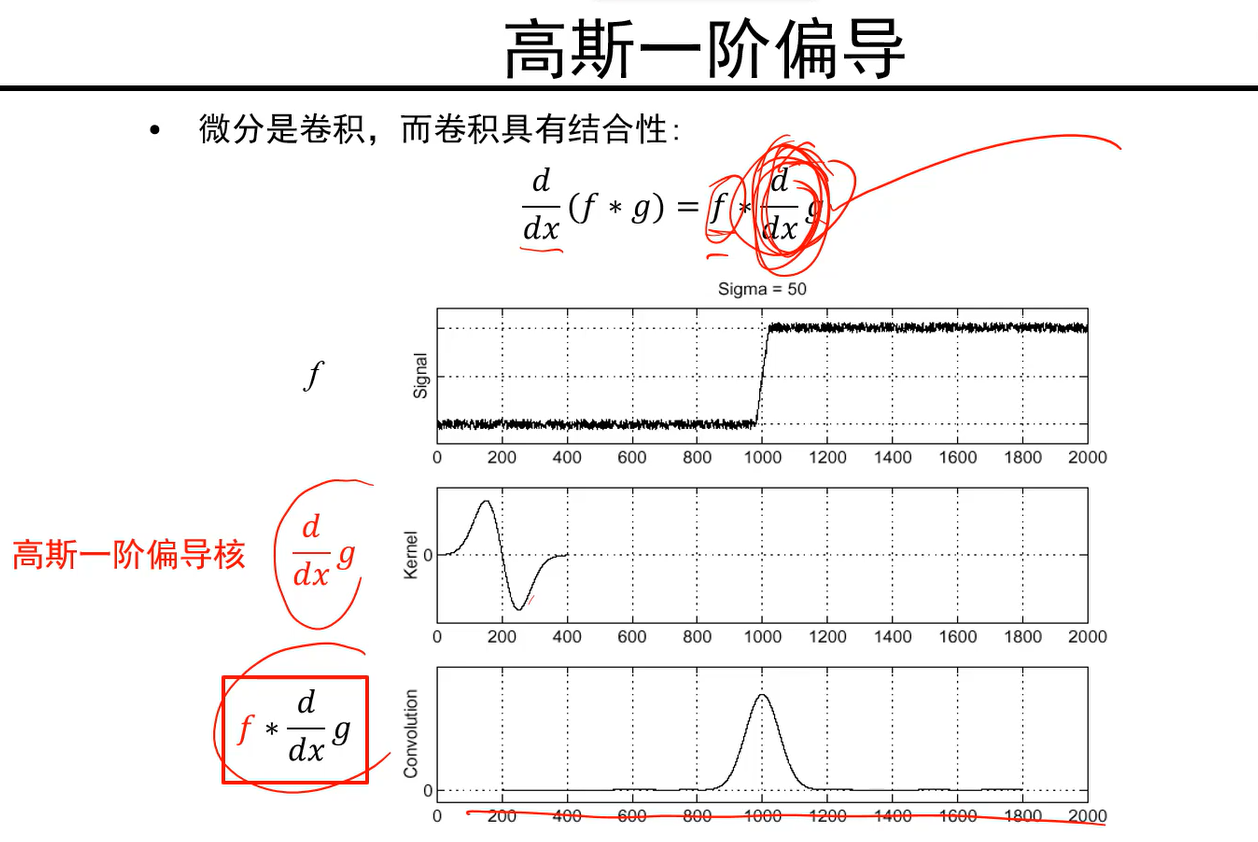
- 但是这样处理有个问题,就是f和g要先卷积一次,结果又要进行求导(求导也是一次卷积操作), 因此要作两次卷积。
- 卷积模板间卷积运算量较小,因此利用卷积结合率,先让高斯模板去做导数,然后再与信号卷积,这样运算量就小了很多。
- 高斯模板导数即高斯偏导模板,用它来做边缘提取更好,同时起两种作用,首先对图像做了平滑,然后又做了求导,
高斯一阶偏导卷积核

- 高斯一阶导模板,因为导数没有参数,因此模板只有一个参数:方差
- 方差不同,关注不同粒度的信息。方差由小到大过程中对信号提取能力是不同的,大方差是提取信号中的粗粒度信息,而小方差提取细粒度信息。
高斯核 vs. 高斯一阶核
边缘检测目标
理想目标如下:
- 但梯度幅值图像得到的边缘图,有些边缘很厚。

- 但非极大值抑制后还会有噪声,因此要把响应值低的去掉。
Canny边缘提取器

- 目前为止最有效的边缘检测器。