Meta Learning

learn to learn

1

我们希望做到的是，机器根据过去任务提取的经验，变成了更厉害的学习者。之后若有新的任务，可以学习的更快，因为从过去的任务里学到了新的学习的技巧。

• 举例来说：教机器做了语音识别，图像识别，然后机器在做文字识别时，能够做的更好。

  • 虽然任务间没有直接关系，但机器从过去的任务中学到了”怎么学习“这件事。

    和LLL的区别： LLL里面不断用同一个模型来学习，期待同一个模型可以同时学会很多技能。 而meta learning，不同任务有不同的模型，每个任务有自己的模型，我们期待的是机器可以从过去的学习经验中学到一些东西，使得在未来在训练新的模型时可以更快更好。

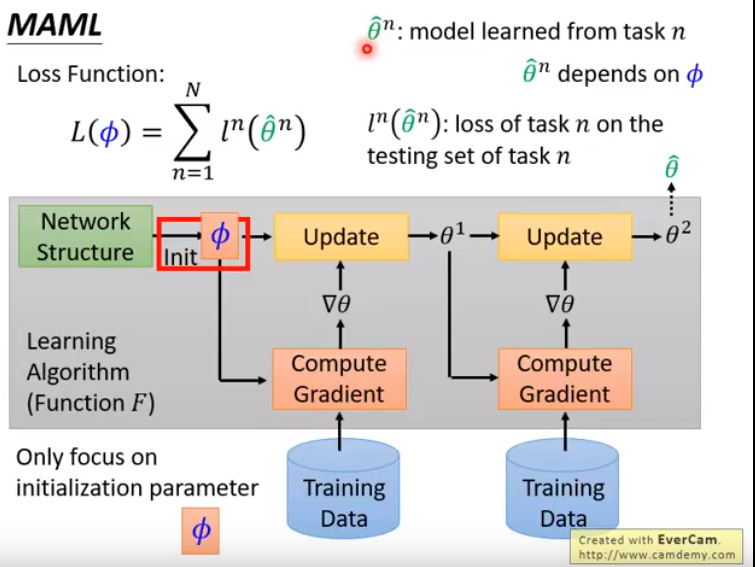
• 回顾一下机器学习的概念，需要一个学习算法，而学习算法是人设计的，将训练资料作为输入，就会吐出CNN的参数，有了参数就得到一个函数f，就能拿来识别新的图像。

  • 根据训练资料找一个函数f的能力。
• 而元学习中，将学习算法也想成一个函数，用F表示，吃进去训练资料，吐出的是另外一个函数f，这个f可以用来做图像识别。元学习要做的就是让机器自己找出F。
  • 根据训练资料找一个函数F的能力，这个F能力是找一个函数f拿来做想让它做的事情如图像识别。
  • F的输入是训练资料，输出是训练后的模型。（如果是拿NN做模型的话，输出就是一个NN，具体来说是里面的参数）
• 机器学习和元学习都是要找出一个函数，但要求函数做的事情是不一样的。

2 define a learning algorithm set

当机器学习时，定义了一个网络架构，就相当于有了一个function set。那么什么叫做一组学习算法呢？
我们拿梯度下降举例。
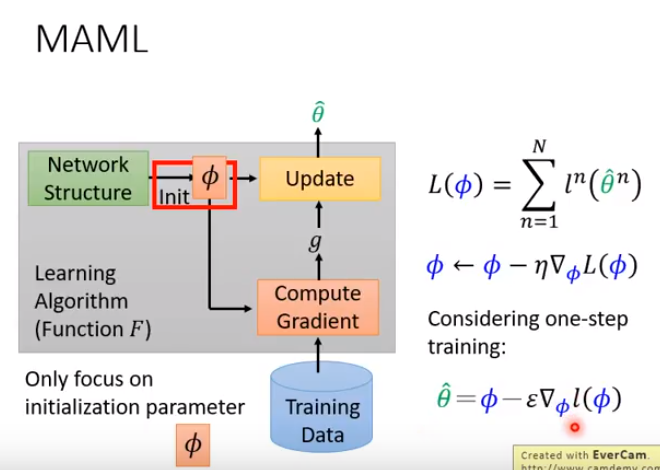
图中，框起来的很多过程（红色圈出的方块）都是需要人设计的，比如网络架构的设计，参数如何初始化，怎么更新参数；并不是机器学出来的。当我们选择不同的设计时，就相当于得到了不同的学习算法。

• 元学习要做的事情就是在红色方块里的一些部分，不要人来设计，让机器自己来学。
  • 比如我们放宽theta0的初始化，让机器自己学出初始化的值。不同初始化的值就可以想成不同的学习算法。

现在我们有了学习算法集，里面有一大堆学习算法，下面需要有办法来衡量学习算法的好坏。

defining the goodness of a function F

• 要知道学习算法好不好，就拿这个学习算法来学一些任务看看。
  • 只有一个测试任务是不够的，要准备一个任务集合来衡量学习算法的好坏。

l1表示学习算法产生出来的函数在任务1的测试集上得出的损失，l2同理。

• 比如我们现在有N个任务，每个任务都算出一个loss值，用l^n表示，相加为L(F)，用来评估学习算法的好坏。

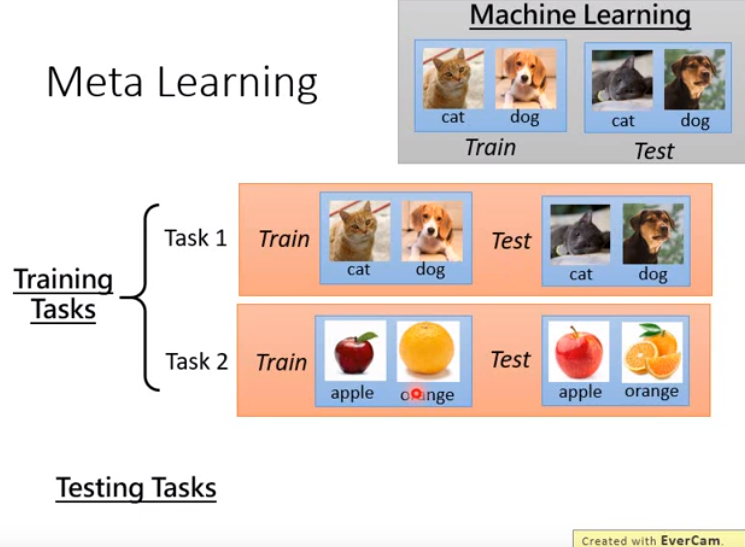
• 由上面可以看出，机器学习和元学习在训练资料上就很不同。
  • 元学习上，要准备的不是训练集和测试集，而是训练任务集和测试任务集。
    • 每个任务里都有训练集和测试集
  • 训练任务和测试任务要不太一样。
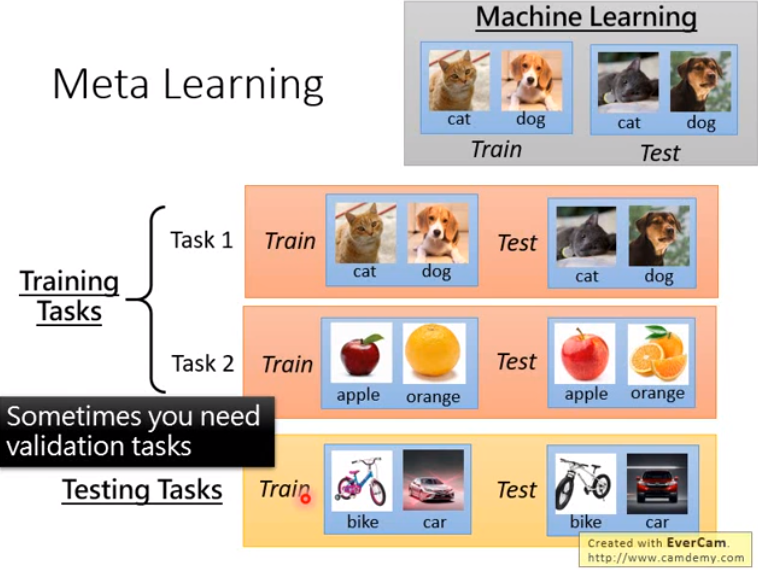
  • 因为有些参数要调整，因此还要从训练任务集中划分出验证任务集。

• 元学习常常和小样本学习一起讨论。（因为如果每个任务都很大，那算法很久才能跑出来，因此这里的每个任务都比较小）
  • 小样本学习里，不会将一个任务中的训练集和测试集直接这样叫，
  • 往往将训练集叫做support set，将测试集叫做query set
    • 原因：support set是每一个训练任务的训练集，而所有训练任务合起来，是元学习的训练集，因此写文章时会混乱，因此改个名字。

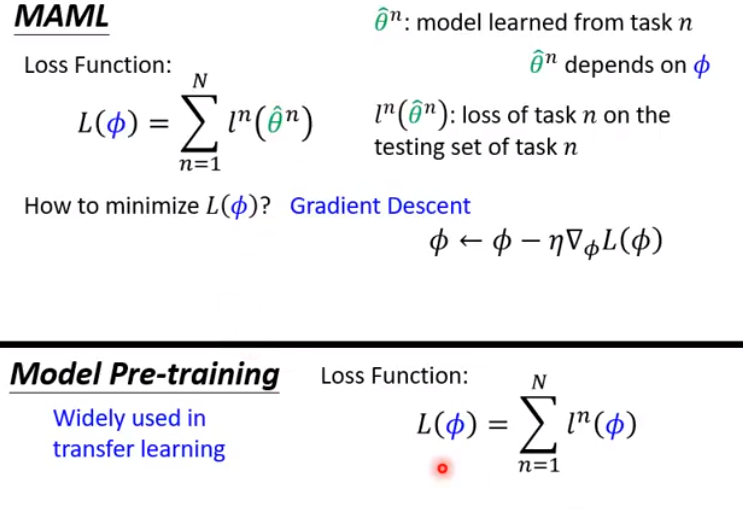
      下面要讲的MAML的目标是找出一个对所有任务都很好的初始参数，接下来如何更新这个初始参数，用的依然是梯度下降。 MAML中即使不同任务的loss不同，也是可以跑的。 但也有其他的元学习做法，学习算法是神经网络的架构，输入是训练资料，输出是神经网络的参数。

find the best function F*

Benchmark corpus

Omniglot

• 数据集的使用：设计成一个小样本分类的任务。
  • 先决定分类任务里面有多少个way（即类别），多少个shot（即每个class有多少example）。
• N-ways K-shot 分类：就是指，在每个训练和测试任务中，有N个类，每个类有K个样本。

例如：

• 实际上训练时，就要将符号分为两类：训练组和测试组。
  • 然后用训练组的字符来制造训练任务。
  • 比如使用N-way K-shot。从训练组随机抽取出N个字符（即抽出N个字符类别），然后从每个字符中随机拿出K个样本。这样就制造出一个训练任务。
  • 测试任务和训练任务产生方法一样，只是测试字符要从测试组里面选。

    注：matching network, protorype network 都可以看作是元学习框架下的方法。

MAML

model-agnostic（模型无关的）meta-learning

• MAML目标是学一个最好的初始化参数（对于所有任务）。
  • 因此MAML限制：要求所有任务的模型结构是一样的。
• MAML和模型预训练的区别：
  • 迁移学习时会用。某一个任务的数据很少，另一个任务的数据很多。
  • 就把模型在数据多的任务上预训练，在只有少量数据的任务上fine-tune。

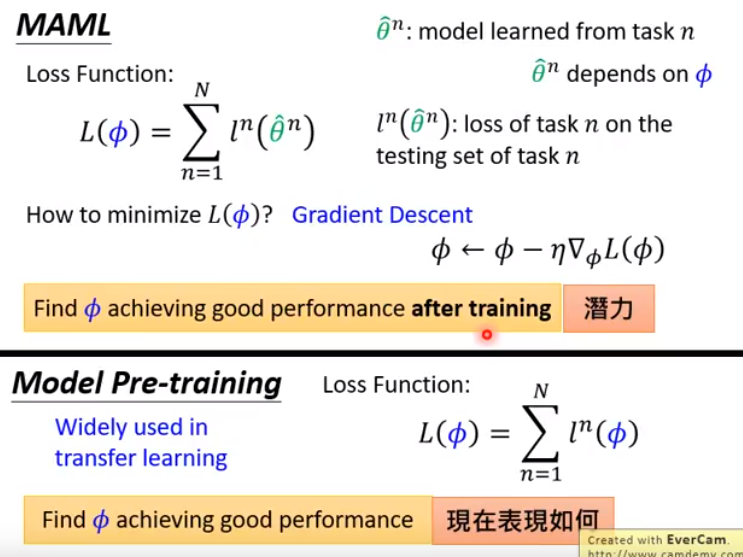
• 区别阐述如下：（对应视频为MAML 5_9）

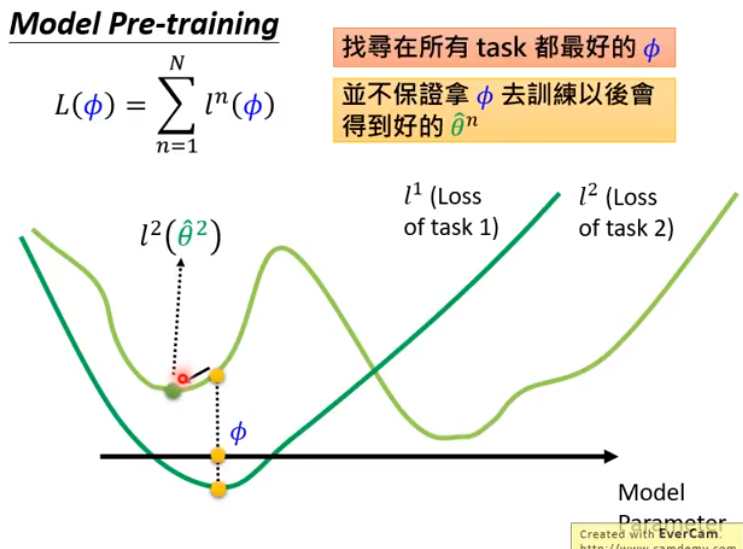
• MAML实际做的时候：
  • 我们假设训练算法只会做一次参数的update，原因如右图所示。
    • 初始参数phi，算过一次梯度后，被update一次后，得到的theta就当成模型最终训练的结果了。
  • 1、为何只做一次，元学习的训练量一般都很大，如果要update几千次，那么每次训练都要比如一个小时，那么这怎么能支撑的住，update一次这样才快。
  • 2、MAML训练目标是在训练后可以得到好的结果，假设能训练出一个很强的初始值，强到这个初始值只要update一次参数，结果就很好。因此只update一次就很好，将这个作为目标，看有没有办法做到。
  • 3、测试时，是可以update很多次的。
  • 4、因为用于小样本数据，数据很少，update多次就很容易过拟合。

Toy Example

展现MAML和迁移学习的差异。

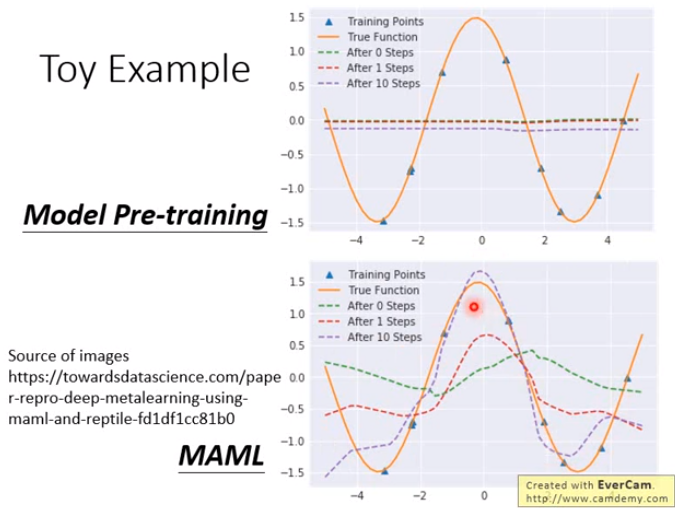
关于MAML是否使用first-order approximation（相当于一种简化），视频MAML_7_9做了数学上的解释。

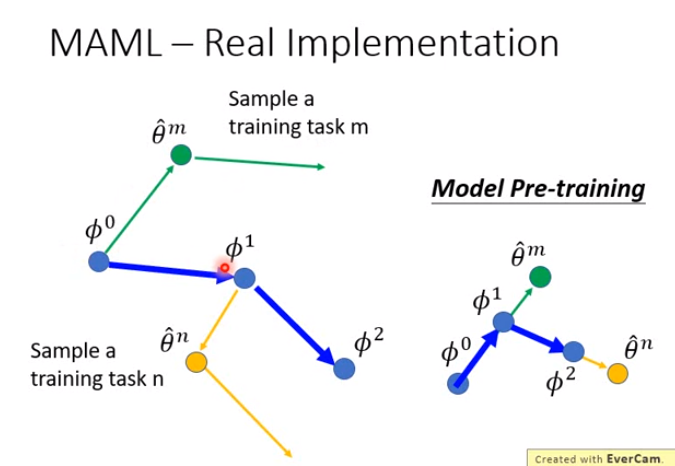
Real Implementation

• phi还是有个初始值的，phi0。接下来要训练phi0，每个任务就是一笔训练资料。在做MAML的时候，也可以sample一个batch的训练任务出来，用task batch来update参数；这里假设做的是stochastic梯度下降，所以一次只sample一个training task出来。
  • 比如sample出来一个task m，用task m去做训练，在MAML里面，我们只update一次参数，变成\theta^m；
  • 再计算一下\theta^m对它的loss function的偏微分，（我们虽然update一次参数就能得到最终最好的模型，但现在故意update两次参数，update出来的第二次参数用来更新phi0为phi1。）
  • phi0变成phi1，移动的方向就跟第二步的梯度算出来的方向是一样的，但大小可能不一样，因为学习率不同。
  • 然后sample出task n，然后task n update一次参数后得到theta^n，再update第二次参数，然后第二次update参数的方向拿去update phi1，变成phi2。
• 实现上和模型预训练的不同：
  • 模型预训练是看现在任务上算出的梯度是怎样，就往这个方向移动。
  • 而MAML是先走两步梯度，拿第二步的梯度来更新初始化的参数phi。

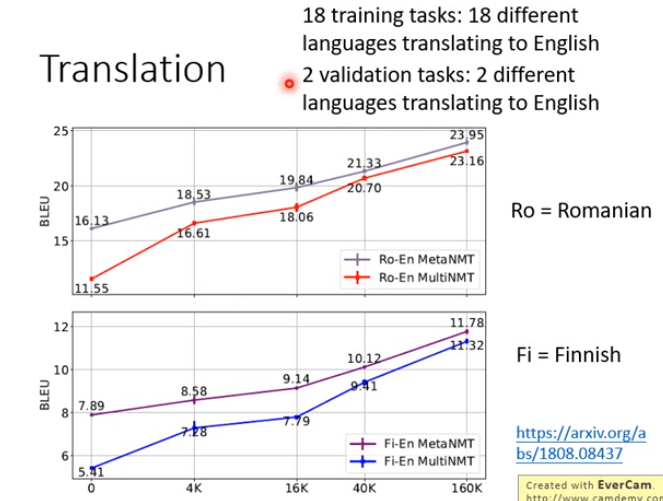
• 在讲MAML时，貌似用到的都是一些不太实际的例子上，那么能否用在实际的task上呢？下面就用到了机器翻译上面。
  • Ro是验证集上的结果，metaNMT是MAML的结果，multiNMT是模型预训练的结果。
  • Fi是测试集上的结果

Reptile

思想比MAML更简单。

MAML、Reptile、Pre-trian的区别：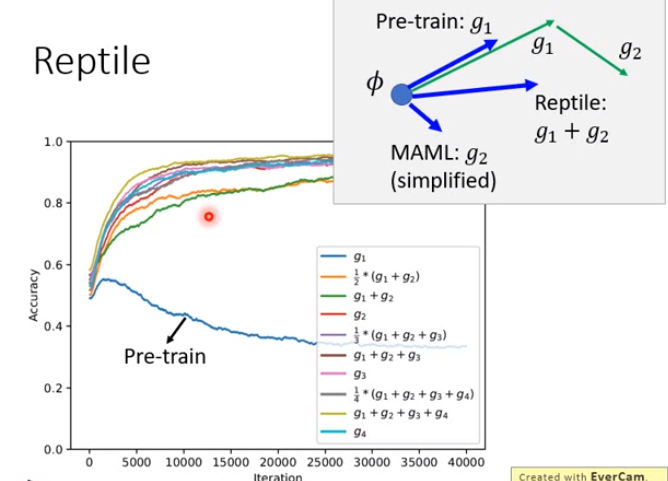

More

除了找初始参数外，有没有方法可以找更多东西呢？如下：

Crazy Idea？

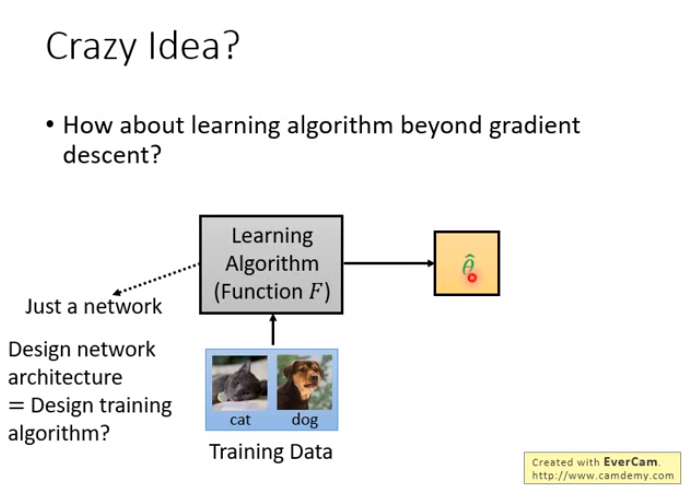
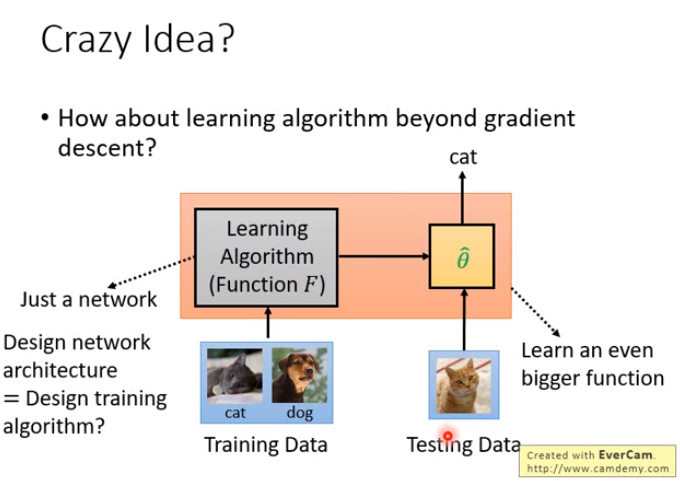
刚才讲的MAML都还是梯度下降，能不能有比梯度下降更厉害的做法呢？即学习算法就是一个神经网络，不管它做的是不是梯度下降，把一堆训练资料丢进去，训练出来直接是我们要训练的模型的参数。
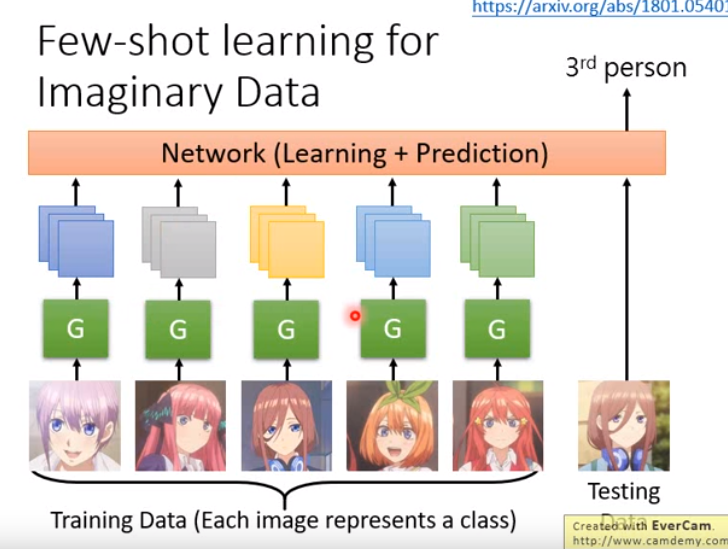
甚至还可以做更疯狂的，如右图。因为学到的theta之后也要用于测试资料，看结果怎么样。能不能够学习一个更大的function，它将训练和测试两个事情都包在里面；这个function就是吃训练资料和测试资料，然后输出测试资料的结果，你连你的model长什么样统统都不知道，它把训练和测试都给你做好了。

Gradient Descent as LSTM

今天讲，如何把熟悉的梯度下降作为LSTM看待，直接把LSTM训练下去，就训练出了梯度下降这样的算法。
上周讲可以学习初始参数，上面这个架构（灰色框里）可以当成RNN看待

• 每一个time step都会吃一个batch的data进来，算梯度。
• 可以把参数看作RNN的memory，前一个time step计算出的参数会在下一个time step拿来继续做运算。

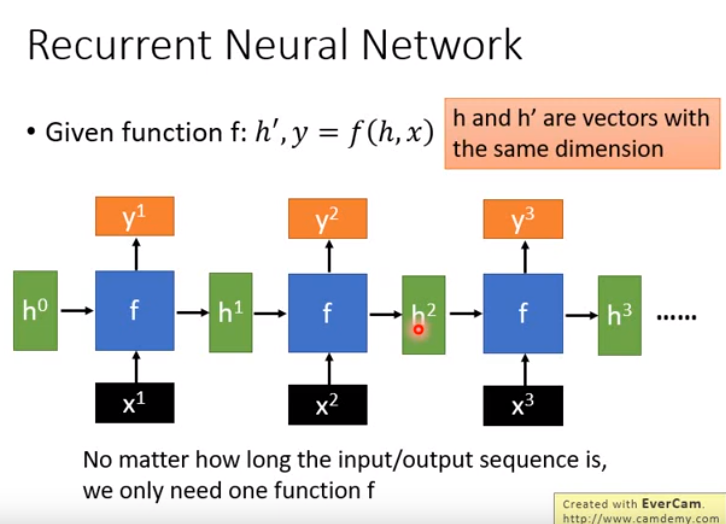
• 简单回顾一下RNN，如图。
  • RNN厉害之处在于，不断以同一个f处理各种输入。不管输入再怎么长，参数量都不会增加。
  • 所以很擅长处理输入是sequence。
• 多数指使用RNN时，用的是LSTM。
  • LSTM特别之处在于将h拆解成两部分。
  • c和h扮演不同角色，输入c和输出c的变化非常小，而输入h和输出h会有较大差别。
  • 因为c^t-1和c^t很像，不会有太大改变，因此LSTM可以储存较长时间的信息。

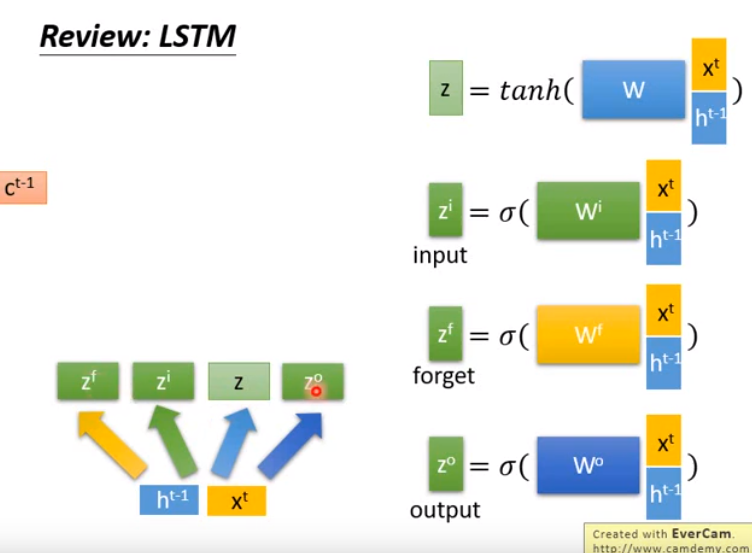
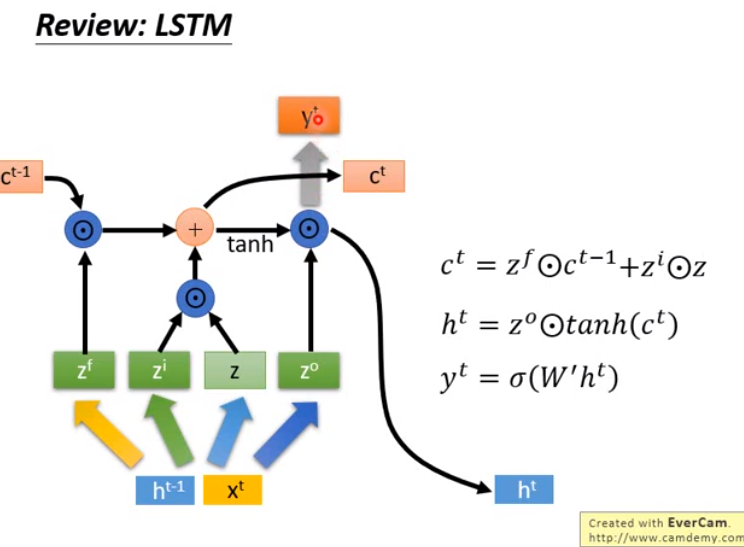
• 简单回顾一下LSTM：
  • z和zi做点乘（element-wise），zi决定z能否通过input gate，以做接下来的运算。
  • zf和c^t-1做点乘，zf是forget gate，决定是使用c^t-1还是遗忘。
  • 接下来将以上两步的结果加起来，得到下一个时间步的c^t
  • 然后计算右图的项
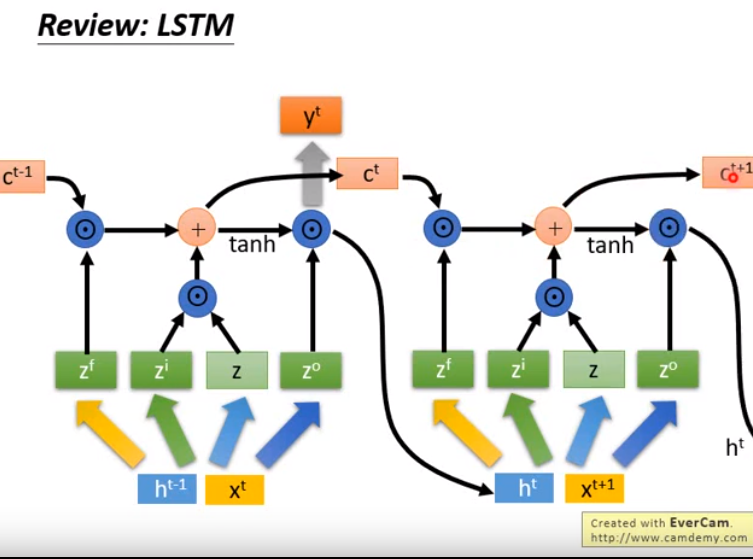
  • 之后得到新的ht，不断循环往复计算下去。

• 那么LSTM和梯度下降有什么联系呢？
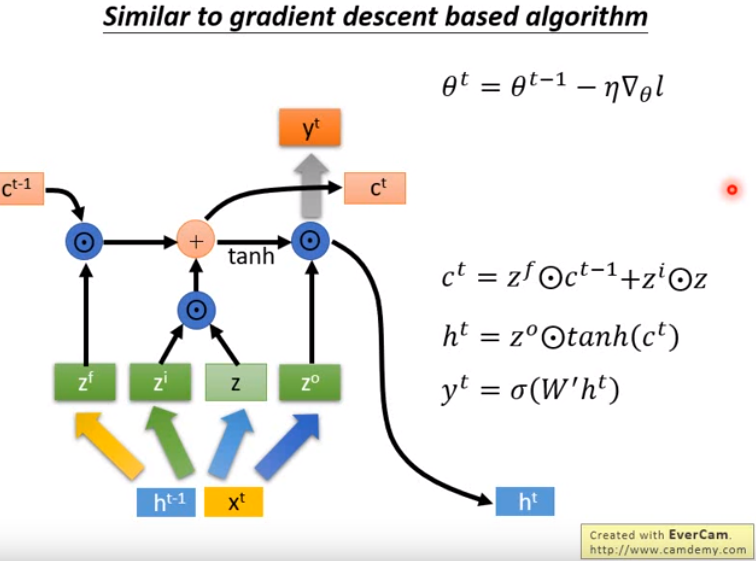
  • 比较梯度下降的式子和计算c^t的式子，可以发现是相似的。
  • 何不就把c当作theta看待，于是现在就把LSTM里面存在memory cell里面的值c当作是神经网络的参数看待。
• 接下来如何让右图下面的式子和上面的式子一致呢？
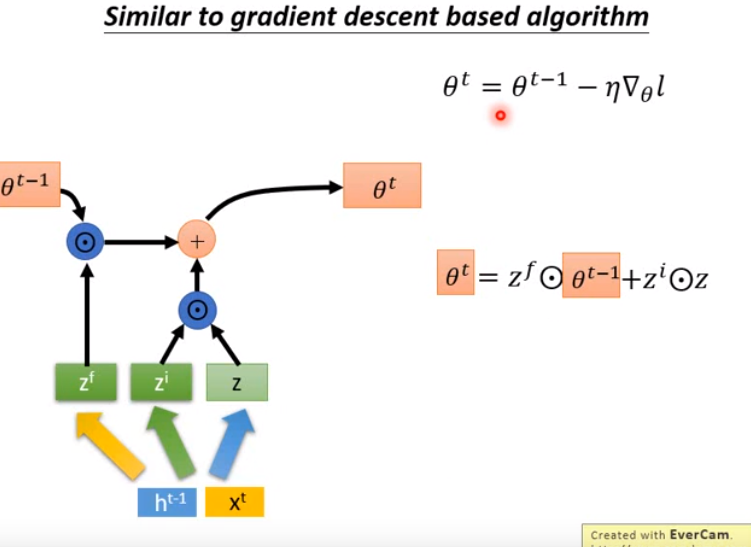
  • 现在的输入是h^t-1（来自上个时间步）、x^t（外界的输入比如一个词汇）；将其换成梯度乘上个负号。
  • 然后让z换成负梯度，让zf永远都为1，zi都是学习率elta。
  • 这样处理之后，两个式子就变成一样的了。
• 因此可以将梯度下降看成LSTM的简化版。
  • 即梯度下降里也有input gate和forget gate，只是值和LSTM不一样，是认为设的，而LSTM这两个值是机器学习出来的。

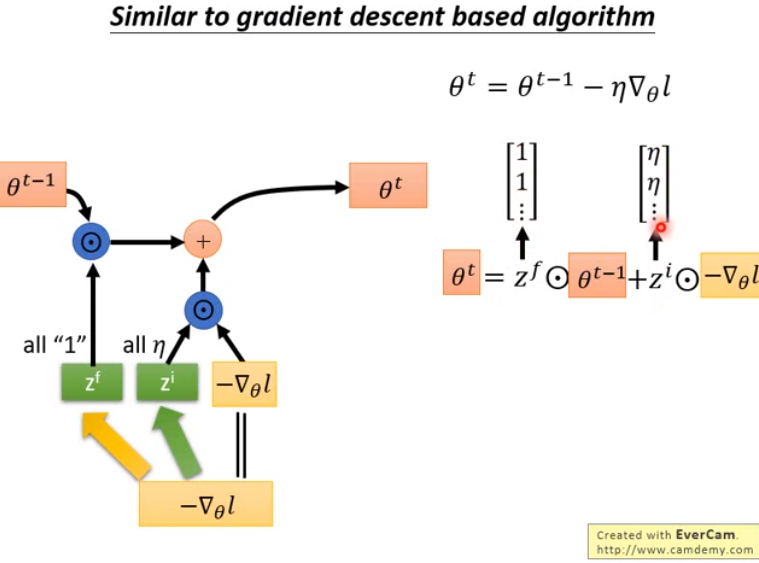
• 那么现在可以理解为梯度下降zf和zi都是人设的，现在能否让它用学习得到呢？
  • 输入部分除了梯度值外，实际操作时可以拿更多信息作为输入。比如theta^t-1算出的loss也可以作为输入。
  • 让机器去学习input gate意味着机器可以动态决定学习率。
  • 让机器去学习forget gate（fortget gate会把之前学出的参数缩小），其实就扮演了类似正则化的角色，即让机器自动学出来要做多少正则化（比如权重衰减）。

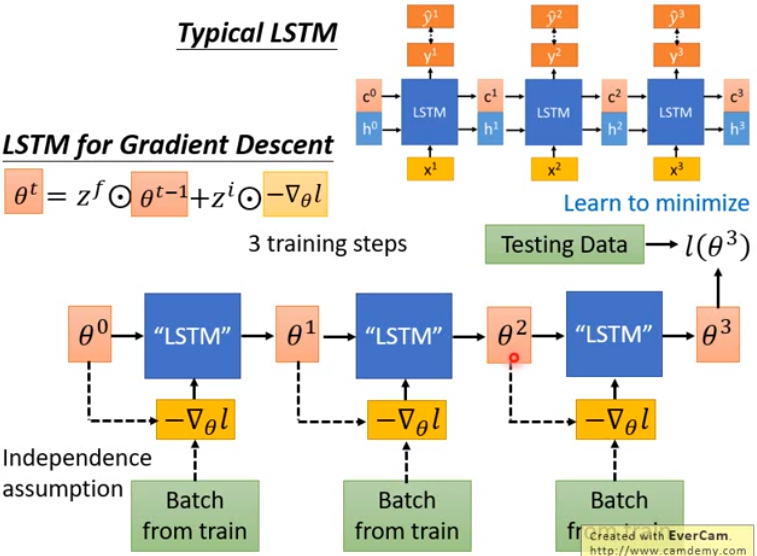
• 典型的LSTM如图中上半部分所示。
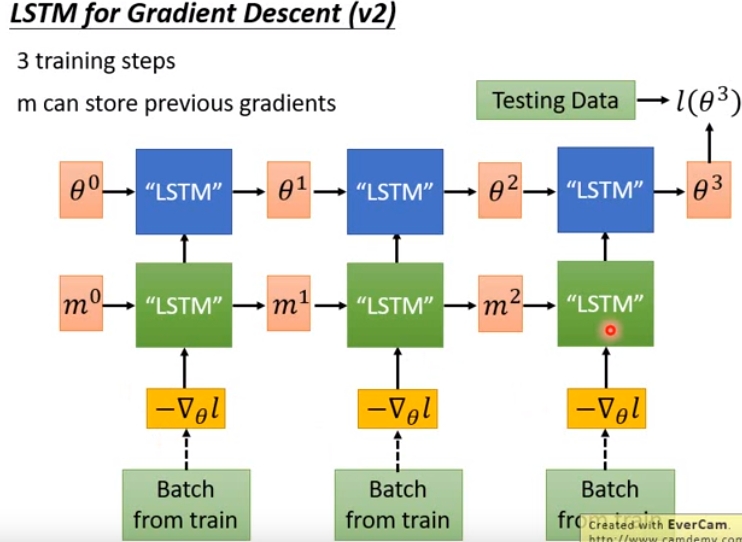
• 梯度下降的LSTM：
  • 一开始有个初始参数theta0，接下来sample一个batch的data，根据data算出负梯度值，将这个值丢到一个LSTM里面进行运算。
  • 这个LSTM的参数，过去是人设好的，现在我们让它在元学习的架构下自动地学出来。
  • 注意，每次sample出的date不同，因此每次输入的梯度都不同。
  • 这里假设我们只做三次theta的update。（实际上训练模型时会做更多次）。接下来就把最后得到的参数theta3拿去测试集上算loss，最终算出的loss就是我们要最小化的目标，然后就会用梯度下降来调LSTM的参数来最小化最终的输出loss of theta3.
• 要注意，梯度下降的LSTM和一般的LSTM有个很大的差别。
  • 一般的LSTM里，x和c是独立的。即memory cell里存的值不会影响你在下一个时间点看到的输入。
  • 而梯度下降的LSTM，theta的值会影响接下来算出的梯度值。
  • 这样反向传播时理论上损失就可以沿着两条路走回来。但这样做会很麻烦，跟一般LSTM就不一样了。
  • 为了 让它跟一般的LSTM更像，就假设两者间的连接不存在。当作一般的LSTM训练下去即可。

• 在输入的地方，LSTM的memory里的初始值是可以通过训练直接学习出来的，因此在此LSTM架构下，也可以做到和MAML一样的事情即把theta0也作为参数，跟着LSTM一起把它学出来。

  Real Implementation

• Q：把LSTM里面的memory cell值看出神经网络的参数，而神经网络的值动辄十万百万，难道要开一个LSTM，里面有十万百万个cell吗？（一般LSTM开1024个cell就要训练很久了）

  • 十万百万个cell也训练不起来，实做时做了很大的简化，即实际做是所学习的LSTM都只有一个cell而已，只处理一个参数，所有的参数都共用同一个LSTM，一百万个参数也同用一个LSTM来处理。
  • 也就是说，学习好一个LSTM后，是直接被用在所有的参数上。虽然这个LSTM一次只会处理一个参数，但同样的LSTM被用来所有参数上。
  • 这里用下标表示整个模型里某一个参数。theta1和theta2用的处理方式是一样的。
    • Q：处理方式一样，会算出一样的值吗？
    • A：不会，比如初始参数是不同的，梯度算出来也是不一样的。

• 这样做有什么好处呢？
  • 这样做，模型的大小合理（十万百万个cell不太可能）。
  • 参数共用一个LSTM处理也是合理的，因为在一般的梯度下降中，如RMSprop，Adam， 所有的参数使用的更新规则也是相同的。
    • 不同的参数在不同的时间点学习率不一样，但确定学习率的规则是一样的。
  • 之前讲的MAML限制训练task和测试task的模型架构要一致（训练的CNN，测试在RNN，这样是行不通的）。然而如果是这样的实现，所有的参数用同一个LSTM来update，这时训练和测试的模型架构是可以不一样的。
• 只有刚才的架构还不够，我们可以进一步思考：
  • 限制人类设计的常用的梯度下降方法，在决定学习率时，不是只看现在这个时间步的梯度，还会考虑过去的时间步的梯度。
• 因此可以做进一步的延申：
  • 现在再加上另一个LSTM，先将梯度丢到这个LSTM，然后让这个LSTM吐出一个东西，来update我们的参数。
  • 下面的LSTM就可能可以做到过去Monmentum做到的事情（比如累加过去的梯度等）。
  • 这个方法是老师认为可以做出来的。
• 实验结果：

Metric-based

实现上周的crazy idea， 实际应用上有用到此技术的，如face identification和face verification。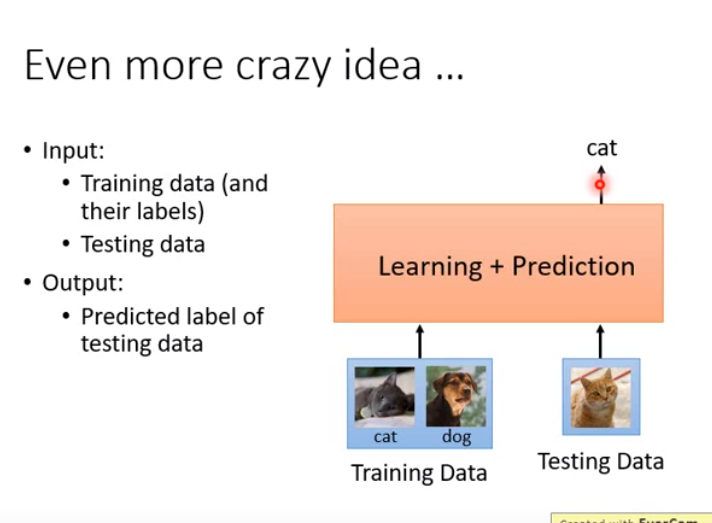

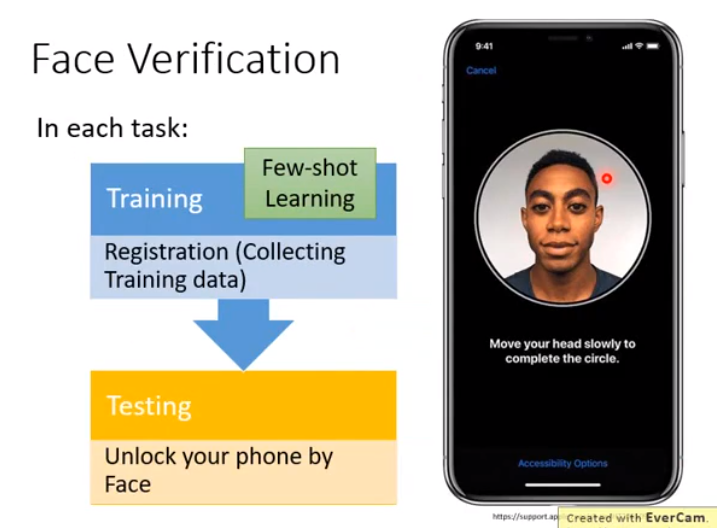
• face verification：判断给的人脸是或不是某个人。
  • 实际上是个小样本学习，比如使用手机时注册的人脸，就是训练资料
• face identification：给一张人脸，判断人脸是为某一组人里面的某个。

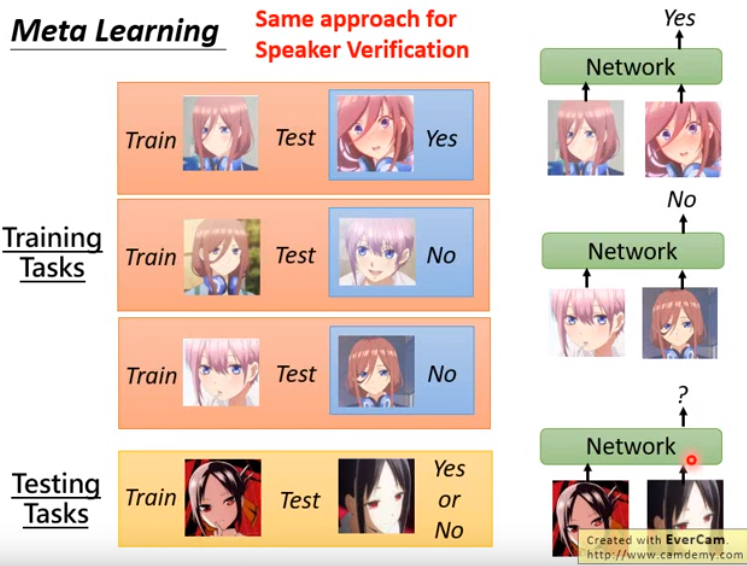
以下拿face verification举例，其实speaker verification做法也是相同的。

• 先收集一些训练任务，网络要做的是输入一个训练资料，输入一个测试资料，直接输出答案是yes或是no
• 测试任务中，测试的脸应该没有出现在训练任务中。

• 我们要训练一个网络，同时做训练和测试。网络架构最常见的一种设计如下：

  Siamese Network

• 如果训练和测试是相同的人，就希望相似度分数越大越好；如果是不同的人，就希望相似度分数越小越好。

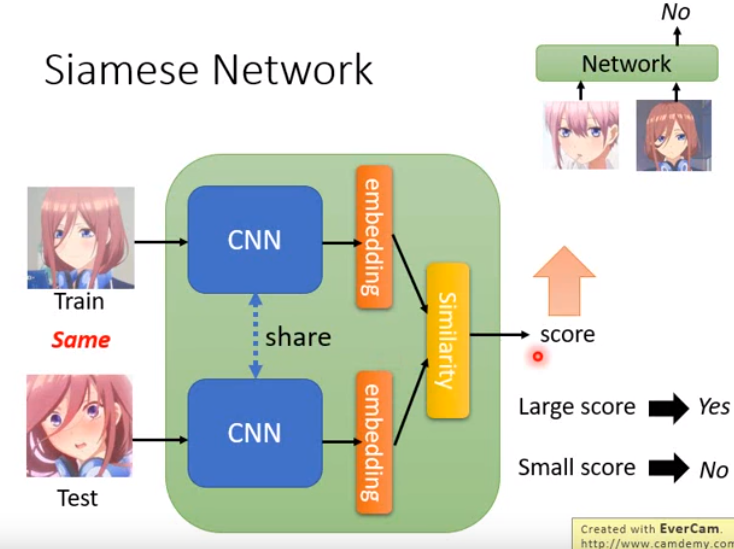
• 孪生网络可以看成一种元学习的方法，因为直接直接吃训练数据和测试数据然后得到输出，但其内部架构很简洁。

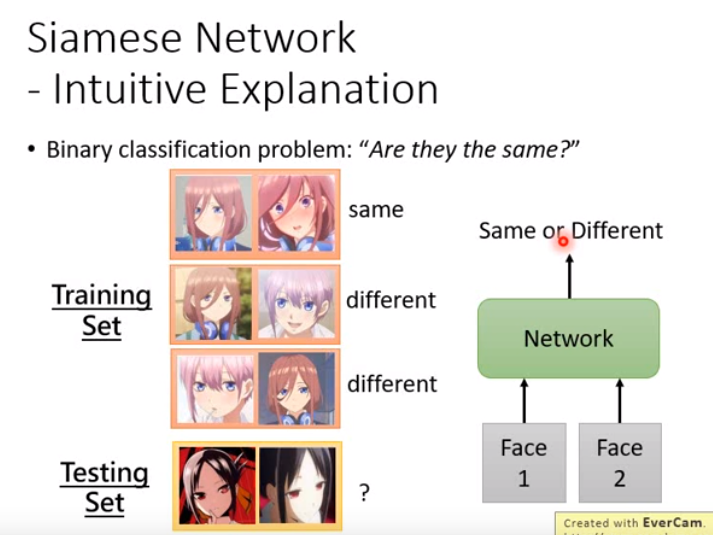
  Siamese Network：Intuitive Explanation

  不见得要从元学习的角度来解释它，可以按如下角度：更容易理解

• 可以说孪生网络就是个单纯的二分类问题，“are they the same”

  • 直接训练一个网络，输入为两张图片，输出为两张图象是否相同；然后应用到测试图像上，就结束了。
  • 每一个training task都是训练时的一笔资料，每一笔资料里都有两张图像，标注信息是两张图像是相同还是不同。

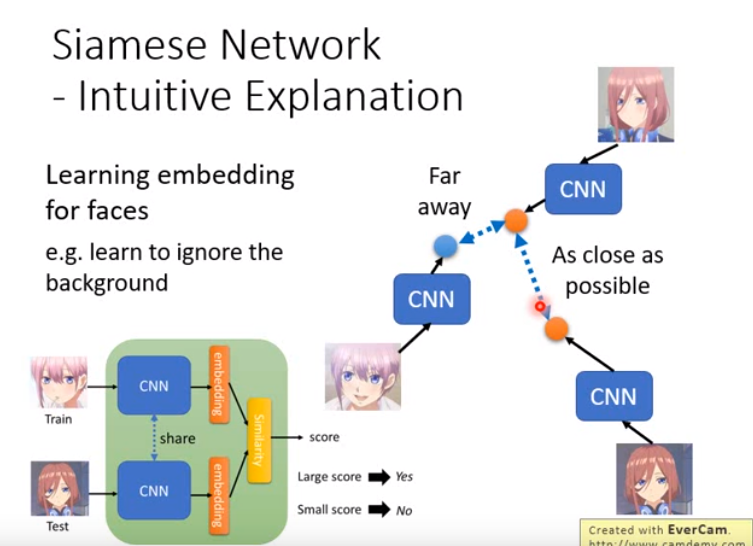
• 内部架构：用CNN将所有人脸都投影到一个空间上，在这个空间上，同一个人的人脸就会比较接近（不管是朝左看还是朝右看），不同人脸会比较远。
• 如何计算两个人在空间的距离呢？

刚才举的例子里面，训练资料都只有一张，要做的事情就是verification，回答yes或no。
现在要做的是identification，即是分类问题，而非单纯回答yes或no。
假设我们现在要把同样的概念用在5-ways 1-shot任务上面。

N-way Few/One-shot Learning

现在五个类每个类只有一张图像，网络就把这五张图像吃下去，测试时，给它一张图像，希望它能自动判断图像是五类中的哪一个类别。
网络的架构有很多做法，如下：

Prototypical Network

做法和Siamese Network类似。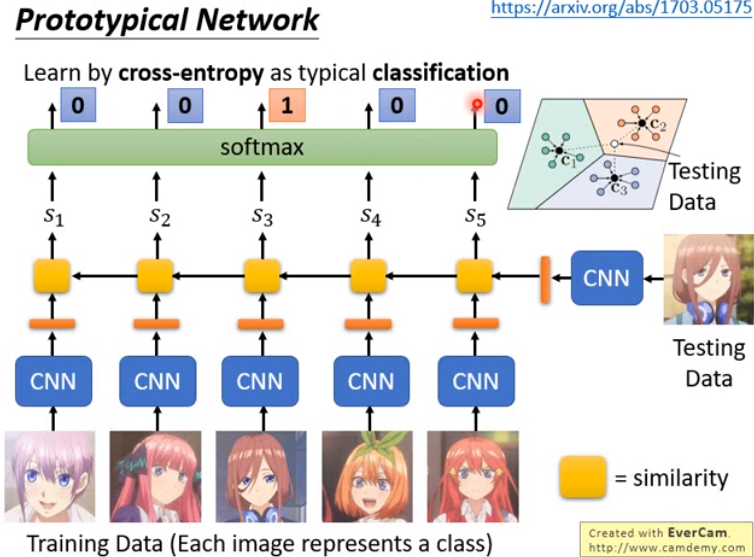

• 举得例子里面假设是one-shot的。如果是few-shot的情况，即每个class不只一张图像，那么原型网络里做的就是：
  • 假设有3个class，每个类5张图像，那么就把5张图像的embedding平均起来。
  • 进来一个测试资料，就看和哪一个类别的embedding的平均最像。
• 这个方法也非常直觉。

  Matching Network

  原形网络中训练数据里的每张图像都分开处理，而matching network认为图像互相之间也是有关系的，因此就直接用一个Bidirectional LSTM来处理。接下来的做法就和原型网络一样的。

  实际上原形网络是后于matching network提出的。因为它认为如果使用一个LSTM处理，那么图像间的顺序不就有影响了吗，这样会很奇怪。

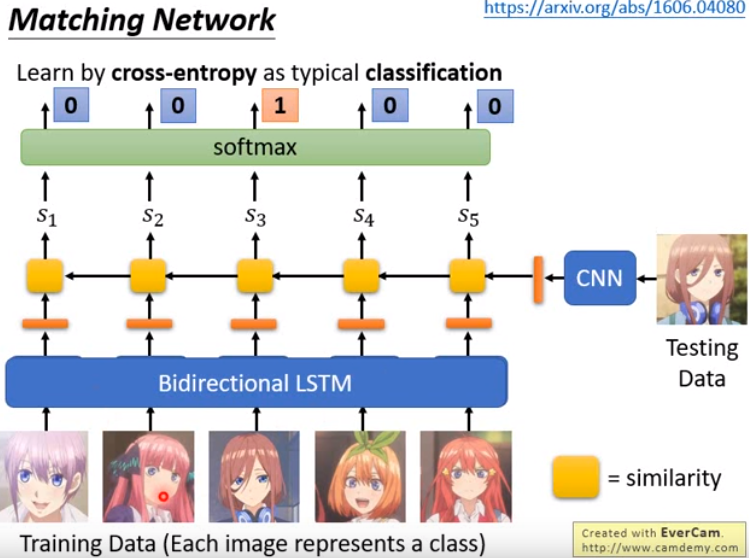
matching network还有个不一样的地方，就是在计算出相似分数后，会通过一个multiple hop的过程，然后才得到最终的输出。

multiple hop这个处理在 memory network中也有用到，两者还挺类似的。 因为没有讲memory network，因此这个处理也没讲，有兴趣可以自己看。

Relation Network

• 和刚才的两个网络不一样的地方：
  • Relation Network先把训练资料中的每张图像和测试资料这个图像，都抽出embedding。
  • 将测试图像的embedding放到训练图像embedding的后面。
  • 本来是计算两个vector间的相似度，关系网络觉得说相似度不是人定的，而是用另一个网络算出来的。
  • 有另一个网络，将合并后的向量吃进去，用它自己的方法计算相似度说这两个vector有多像。
  • 怎么算相似度和怎么做embedding是一起被学出来的。

    Few-shot Learning for Imaginary Data