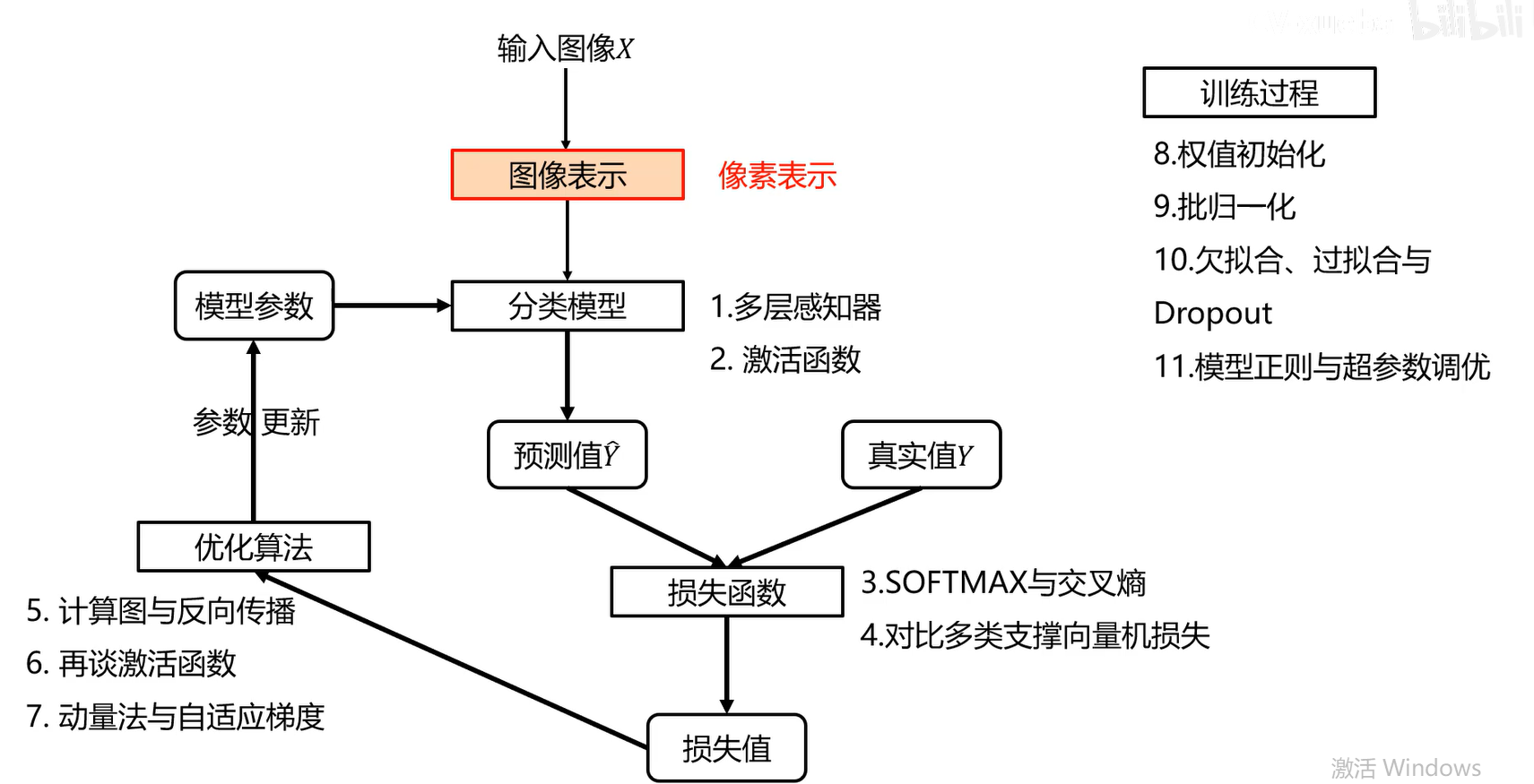
04 全连接神经网络（上）
设计一个分类器的各个步骤
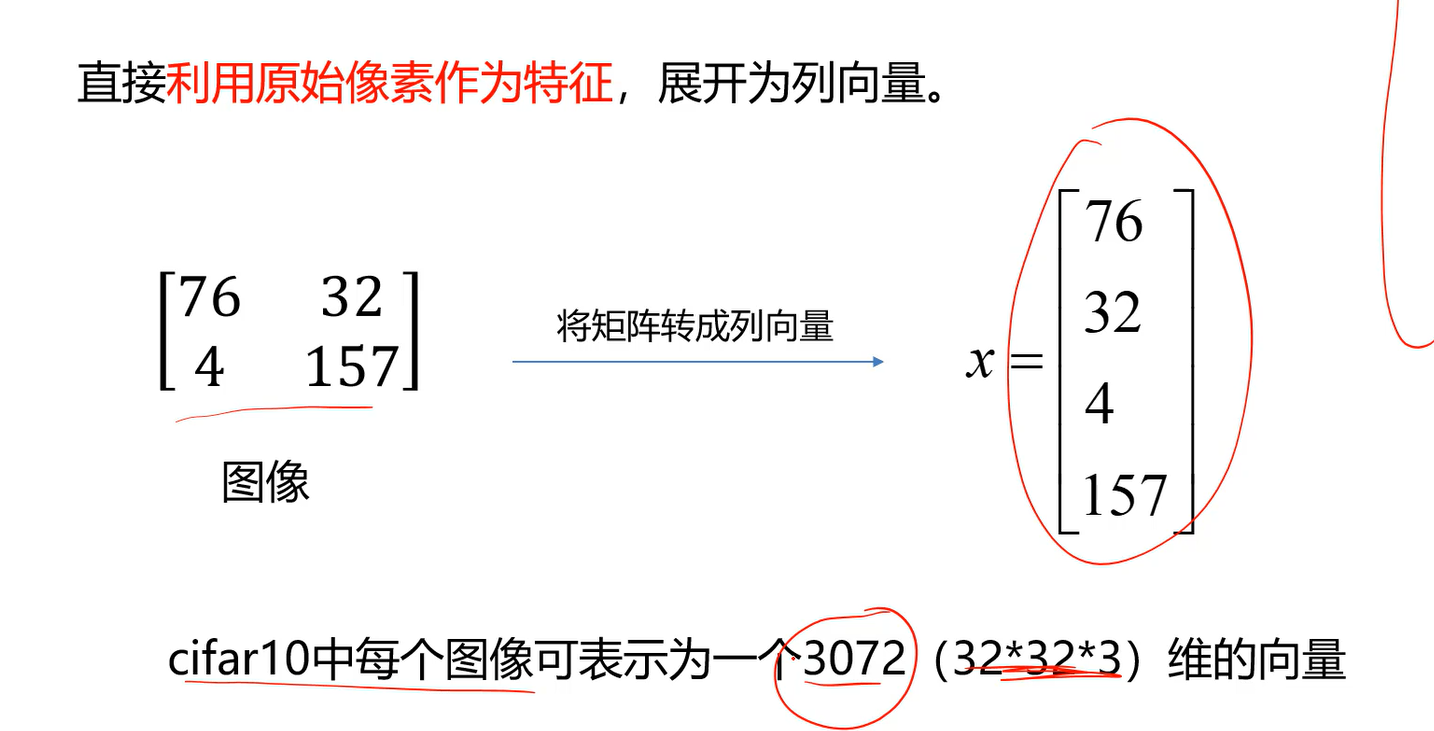
如何表示图像
线性分类器
对于线性分类器，
其中，x代表输入图像，维度为d；f为分数向量，维度为类别个数c；W为权值矩阵，行数为类别数（每个类别都有一个权值向量），列数为特征维度；b为偏置向量，行数即为类别数，每个类别都有个偏置量。
全连接神经网络（多层感知器）
不同于线性分类器，不是给一个x，通过一次线性变换就输出结果，会级联多个变换来实现输入到输出的映射。
全连接神经网络的核心还是线性分类器，但是多了非线性操作。非线性操作是不可以去掉的，否则就不是全连接神经网络的，又变成了线性分类器。
:::info
后面会递推
:::
全连接神经网络的权值有启发
Q：线性分类器级联的构架，真实情况是如何工作，为什么会有效，如何直观理解。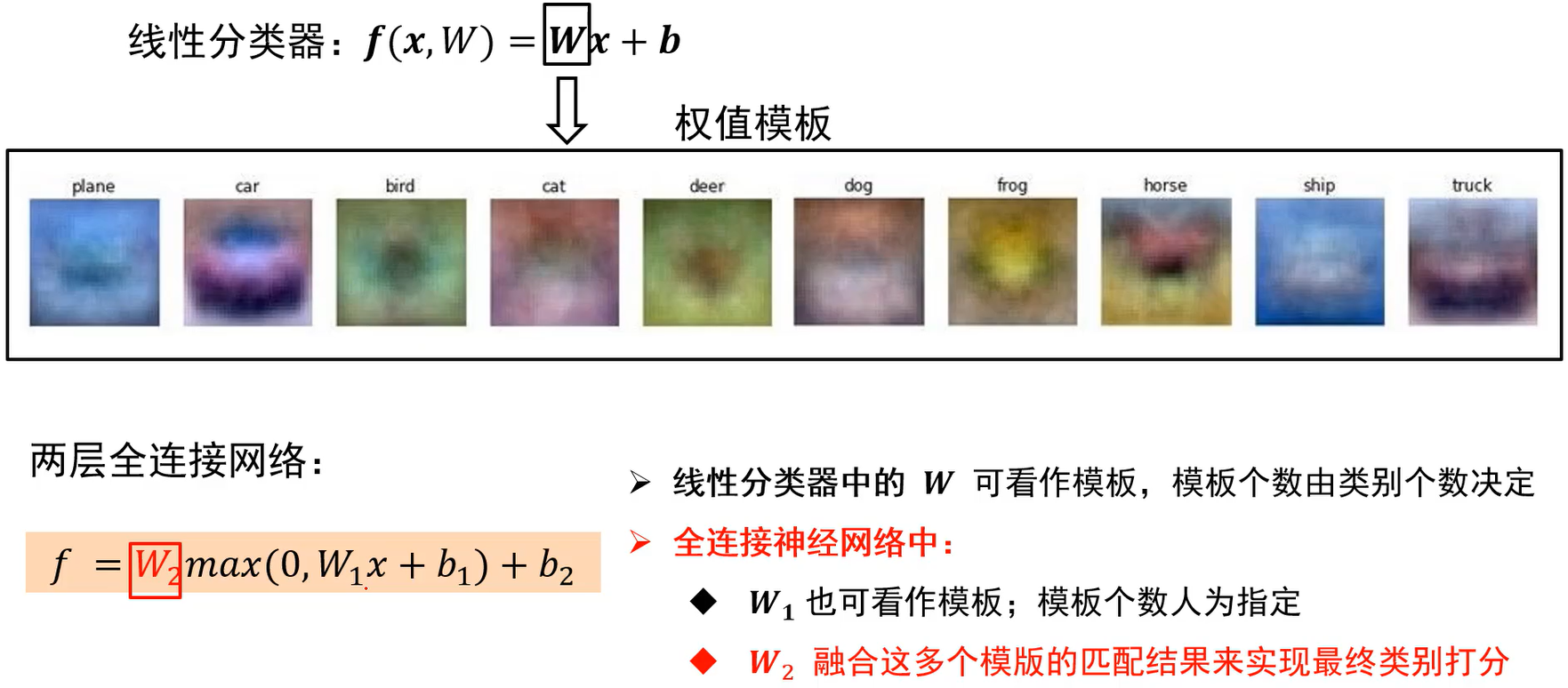
两层全连接网络中，W1的行数人为指定，W2的行数就必须为类别数了。 max为逐元素的操作。
Q：指定W1的行数有何作用呢？
A：比如在原来学的马里面，数据集有两个方向的马头，马的模板要去记录马，平均一下因此模板里会有两个方向的马头；显然模板记录的马是不准确的马。如果模板数够多，比如W1行数为100，也就是有100个模板，那么可以用一个模板去记录正向的马，另一个模板记录朝另一个方向的马；只要模板够多，就有机会学到真正的马长什么样。这就是全连接神经网络第一层权值重要的地方。
Q：两层神经网络为何比线性分类器好
A：W2通常用来融合多个模板的比较结果然后给出结论。W2通常用来融合当前x在低层各个模板的响应结果。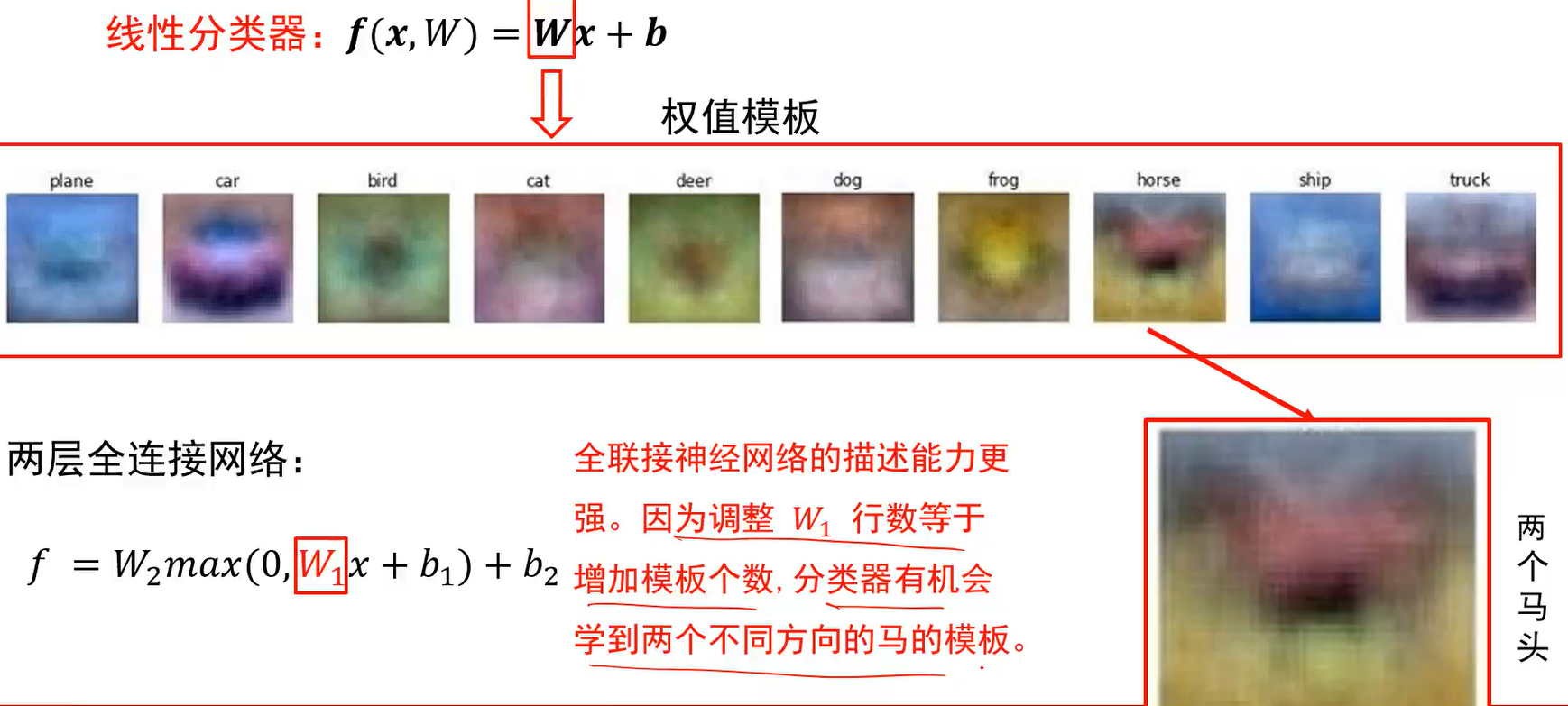
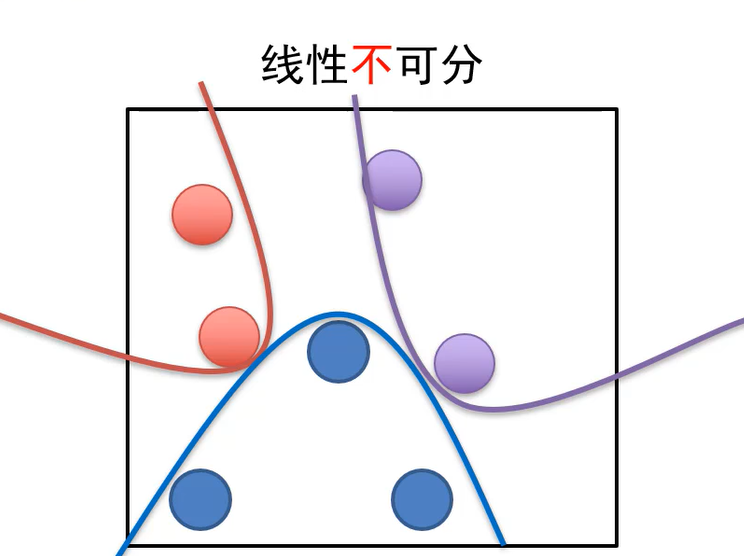
全连接神经网络与线性不可分
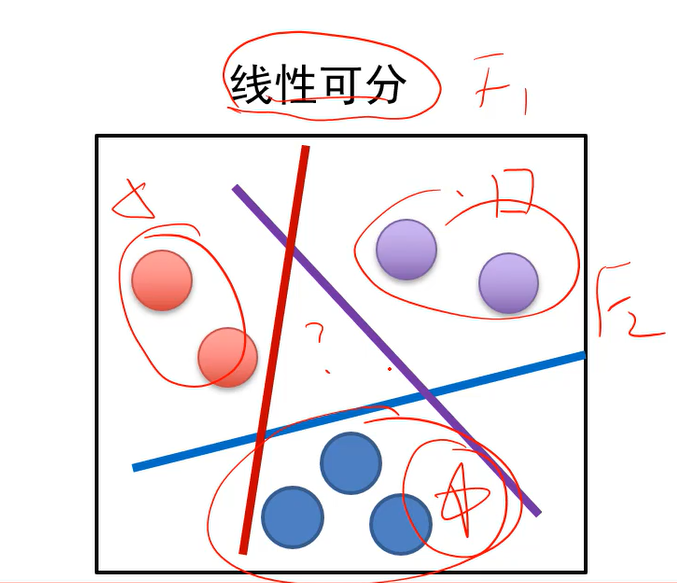
- 线性分类器解决的是线性可分问题。
- 线性可分：至少存在一个线性分界面能把两类样本没有错误的分开。
- 如果任务的样本是线性不可分的话，这时候就要求助于全连接神经网络这样的分类器。
全连接神经网络绘制与命名
:::info
全连接神经网络其实是将线性分类器经过非线性操作后级联起来，想写几层全连接网络就级联几次线性分类器。
:::
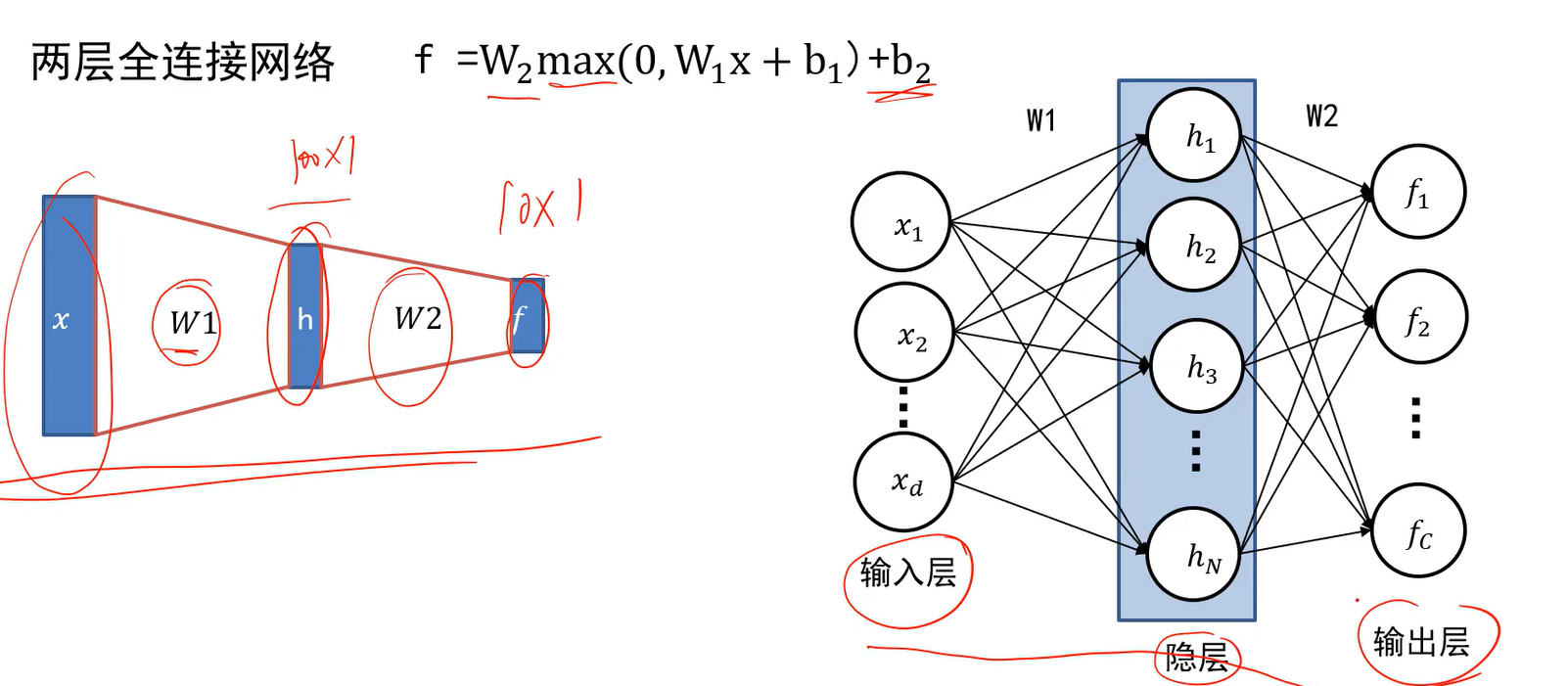
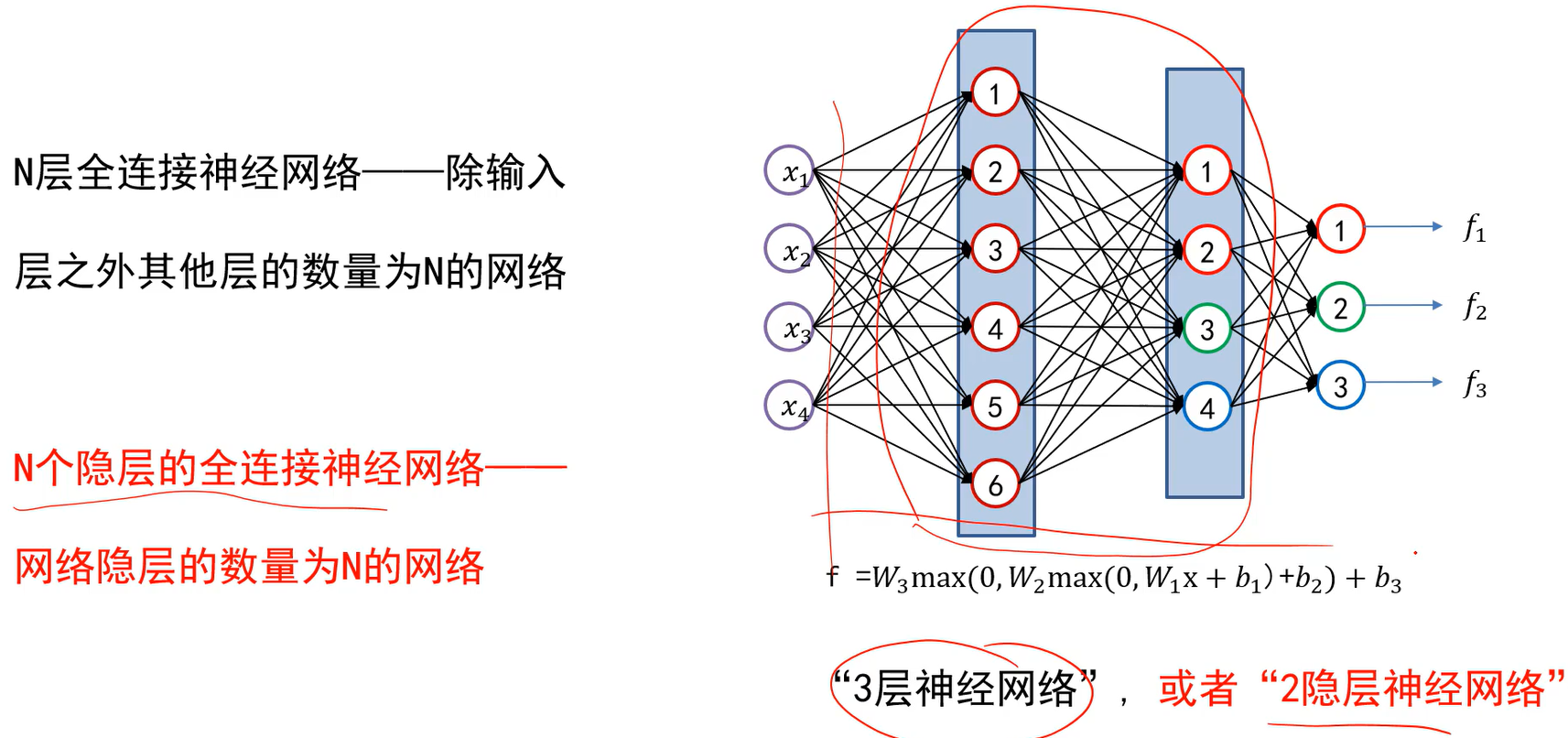
图中W1中包含了b，为了简化才没有单独写出来。 隐层即模板的个数，输出层的个数是固定的，即类别数。
- N层全连接神经网络：除输入层之外其他层的数量为N的网络。
激活函数
Q：为什么需要非线性操作？
A：去掉激活函数后，全连接神经网络将变成一个线性分类器。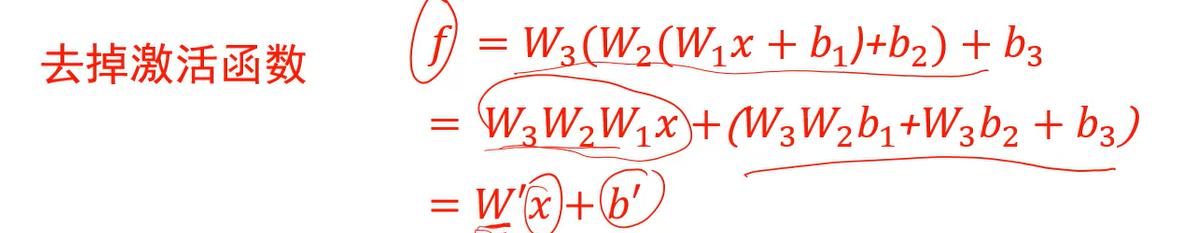
常用的激活函数
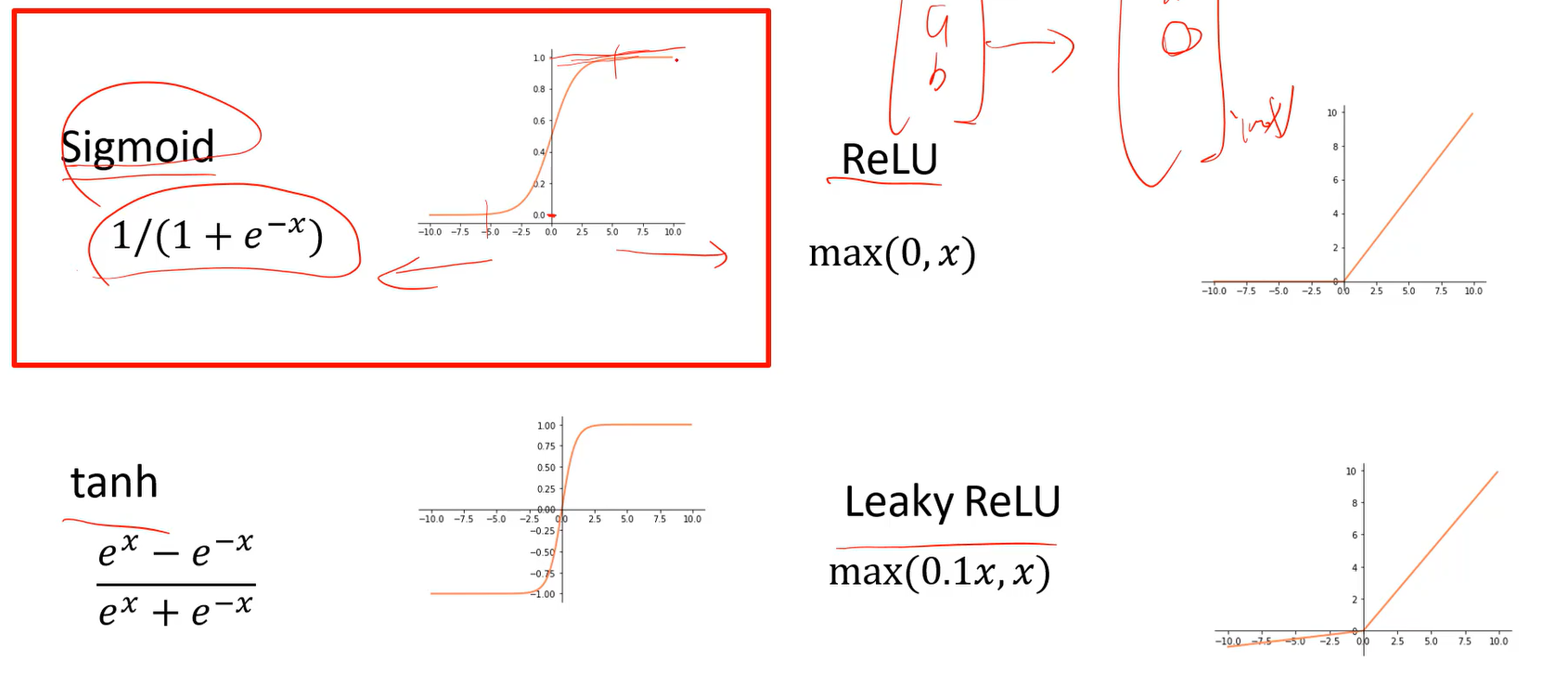
激活函数会对前一层输出的向量中的每个维度分别进行处理。
网络结构设计
1、用不用隐层，用一个还是用几个隐层？（深度设计）
2、每隐层设置多少个神经元合适？（宽度设计）
没有统一的答案。
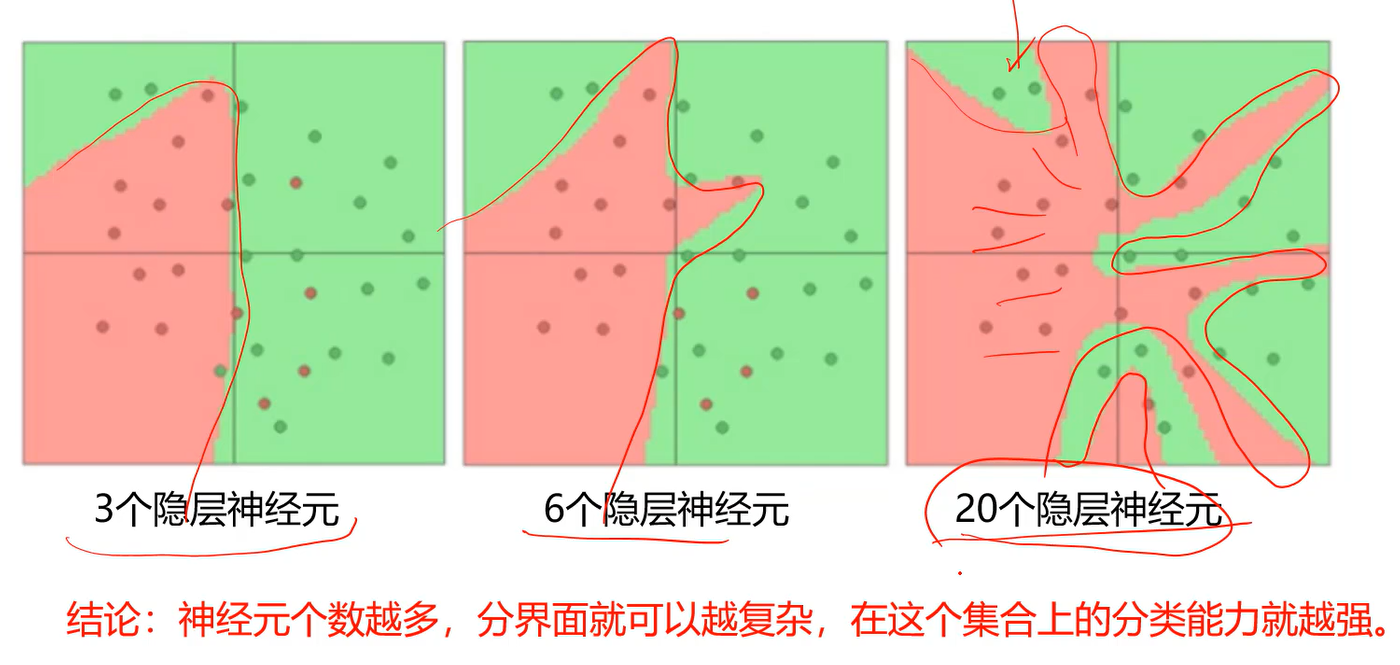
- 结论：神经元个数越多，分界面就可以越复杂，在这个集合上的分类能力就越强。
全连接神经网络小结
Softmax与交叉熵（softmax让网络可以输出概率）
现在预测的时候，只能求出输出层最大的分数，比如f3，然后将其下标作为预测的类别，比如第3类。分数的取值范围为负无穷到正无穷。
而我们想知道做这个决定的正确的可能性，通过现在的输出达不到这个效果，因此引入下面的softmax操作。
softmax操作后，输出层就是一个概率分布。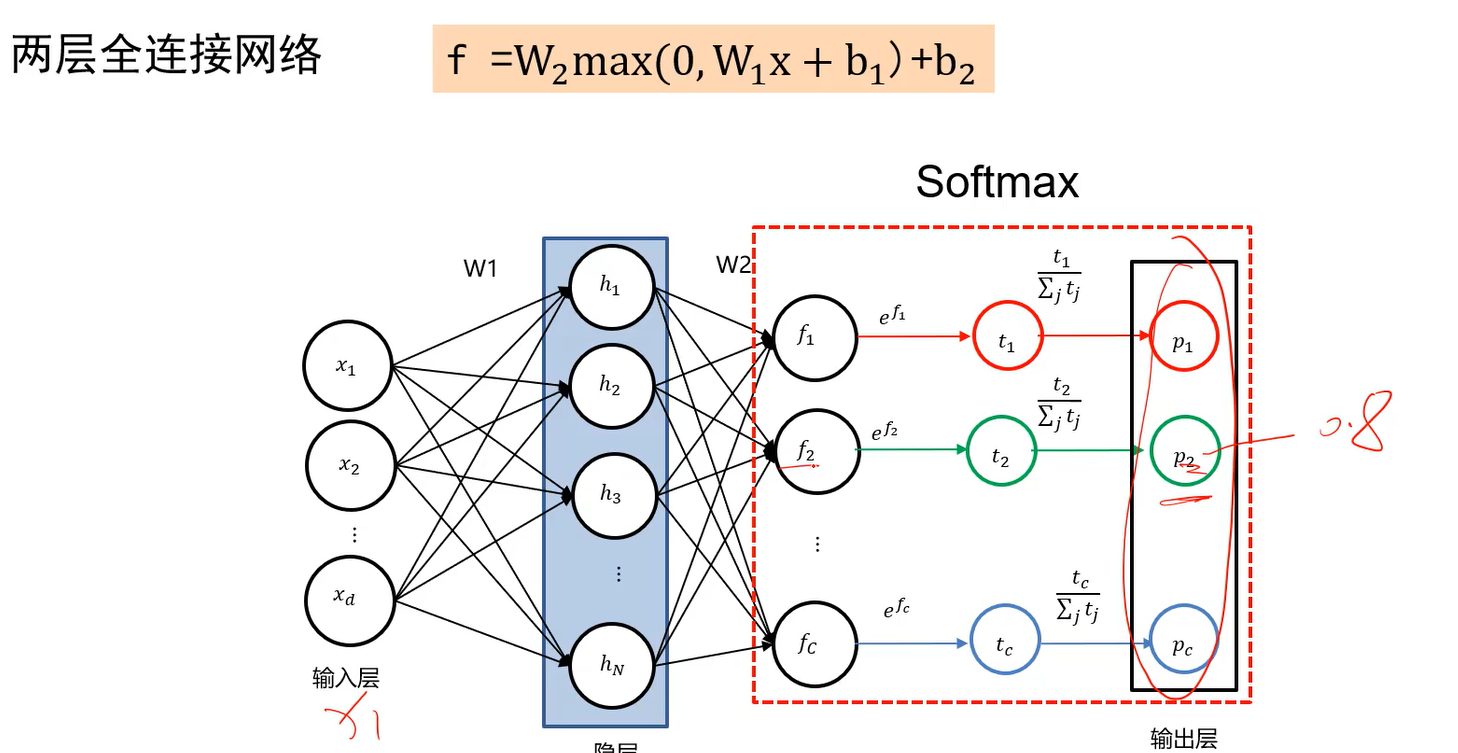
交叉熵损失（计算输出和标准答案间的距离）
Q：如何度量现在的分类器输出和预测值之间的距离？
A：需要比较图中两个分布之间的距离，这就是交叉熵所作的。当两个分布越接近时，交叉熵的损失值就越小。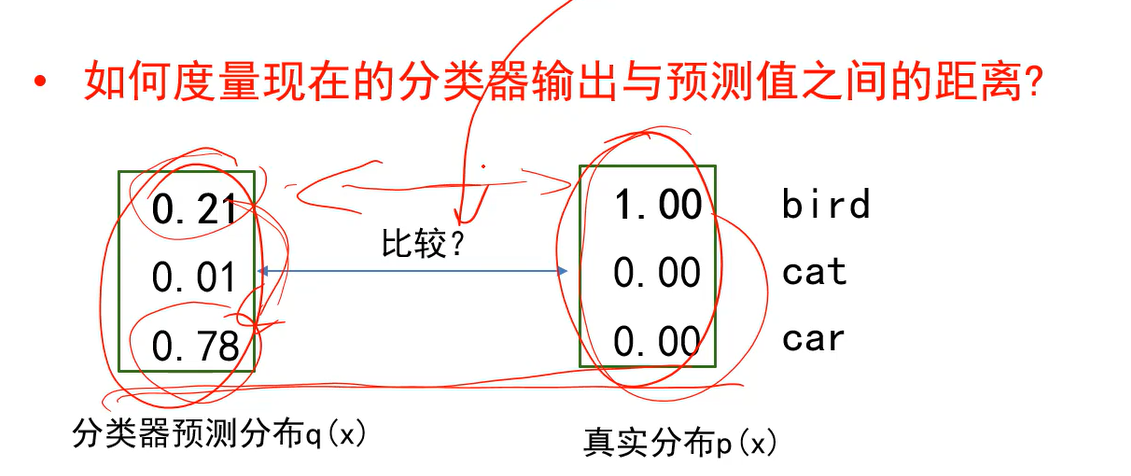
真实分布用one-hot向量表示的。 上述距离不能用多类支撑向量机损失来度量，因为它不考虑右侧，只考虑左侧比如车的答案和鸟的答案之间的关系，大过1没有。无法考虑两个概率分布之间的关系。
交叉熵
- 熵：信息量的体现。当信息量大的时候，熵就大。比如巴西队和中国队足球比赛，中国队基本必输，这时候熵就小。
- 比如[胜,负,平]的概率为[1,0,0]，则熵算出来就为0，当每种情况出现的概率都为1/3即一样时，计算出来熵最大。
- 交叉熵：是p和q两个分布之间的关系。x也是对每种可能性进行的求和。
- 相对熵
- 为什么叫散度（不相似性）不叫距离，距离满足可交换性，但散度不满足。
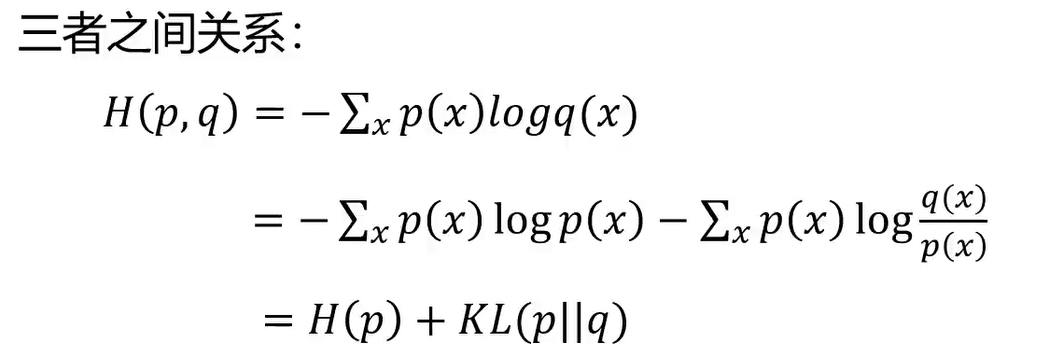
- 真实的p通常就是one-hot向量即标准答案，[1,0,0]，此时熵为0，则KL散度就等于交叉熵。所以就可以用交叉熵来度量两个分布之间的距离。
- 真实分布为one-hot形式时，交叉熵损失简化为：
交叉熵损失 vs 多类支撑向量机损失
Q：相同分数下两种分类器的损失有什么区别？
A：交叉熵在下面第二种情况下并没有停止训练，因为不仅要求预测类别分数高，同时要求其他类别分数低。而多类支撑向量机损失只要比别人高1分就行了。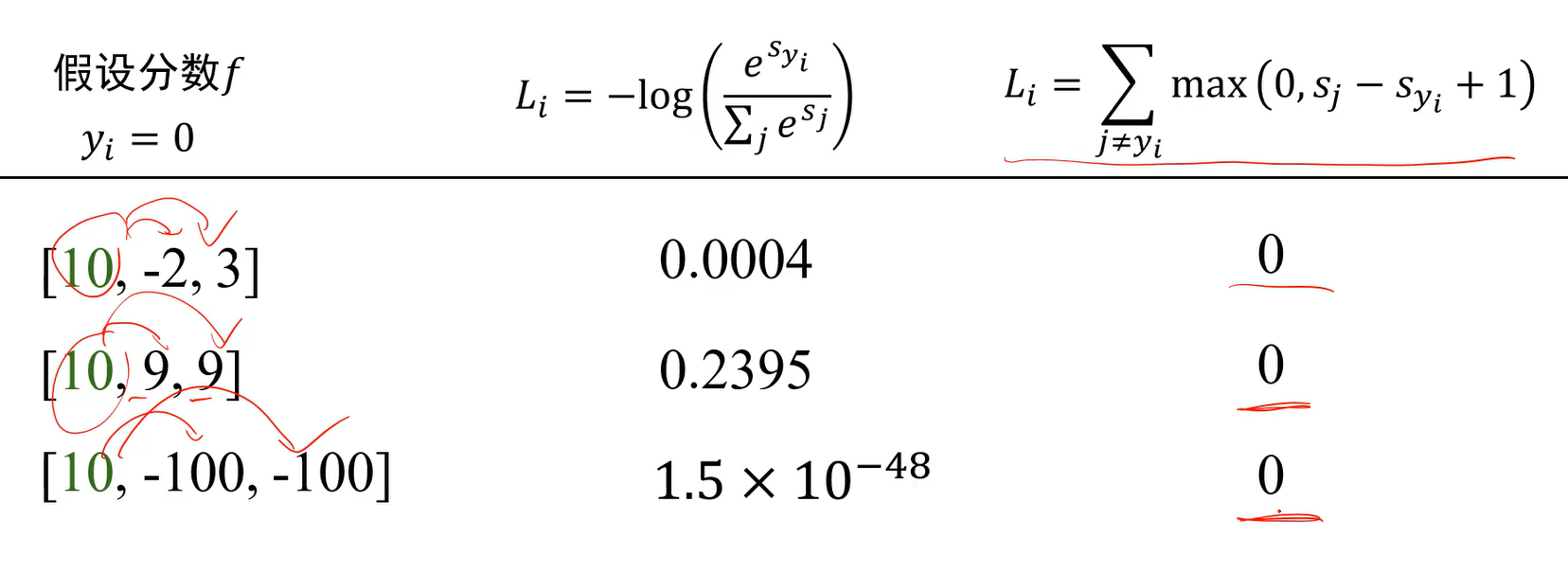
总结
1、softmax操作能让神经网络的输出从绝对的数值变成概率分布
2、交叉熵能度量输出的概率分布与真实的标签（一般为one-hot形式）之间的距离
优化算法
计算图：让计算机实现任意复杂函数的求导问题
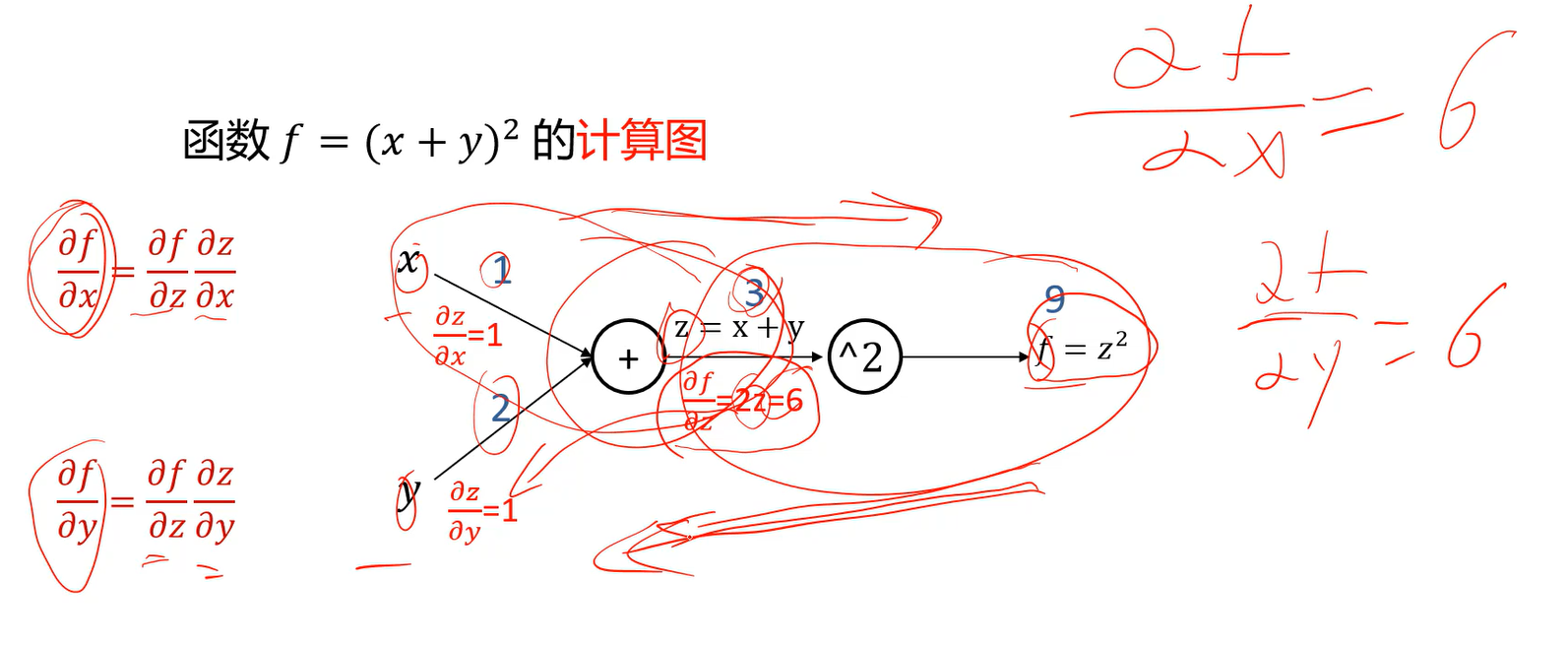
- 计算图上前向计算可以由输入计算出输出。
- 反向计算可以得出输出相对于输入的梯度。可以算出各局部梯度，由链式法则，相乘即可得到梯度。
- 计算图可以算出输出相对于图上所有单元的梯度（不仅是对输入的梯度）
计算图总结
:::info
由于链式法则一路都在做乘法，会存在一些问题。如果局部梯度都比较小，那么每乘一次，数值就变小一次，如果操作叠加的越多，那么梯度信息传着传着很快就没了。这也叫梯度消失问题。
:::
计算图的颗粒度
我们可以将红框中的当成一个整体来看，直接用下面的公式计算这个框的输出和输入间的局部梯度，然后再乘上游梯度。这也就将原本四五次的操作一次完成。
因此计算图中有个颗粒度问题，计算图中的某个门，可以是个复杂的函数，也可以是简单的加减法；我们可以将一些已知的函数，如sigmoid，将其导数求出来，然后把它当作一个基元，这个函数的颗粒度较大，但是计算此函数时计算效率就变高了。
如果完全交给tensorflow，颗粒度较小，计算效率较低，因此有时候可以手写复杂函数的梯度
计算图中常见的门单元
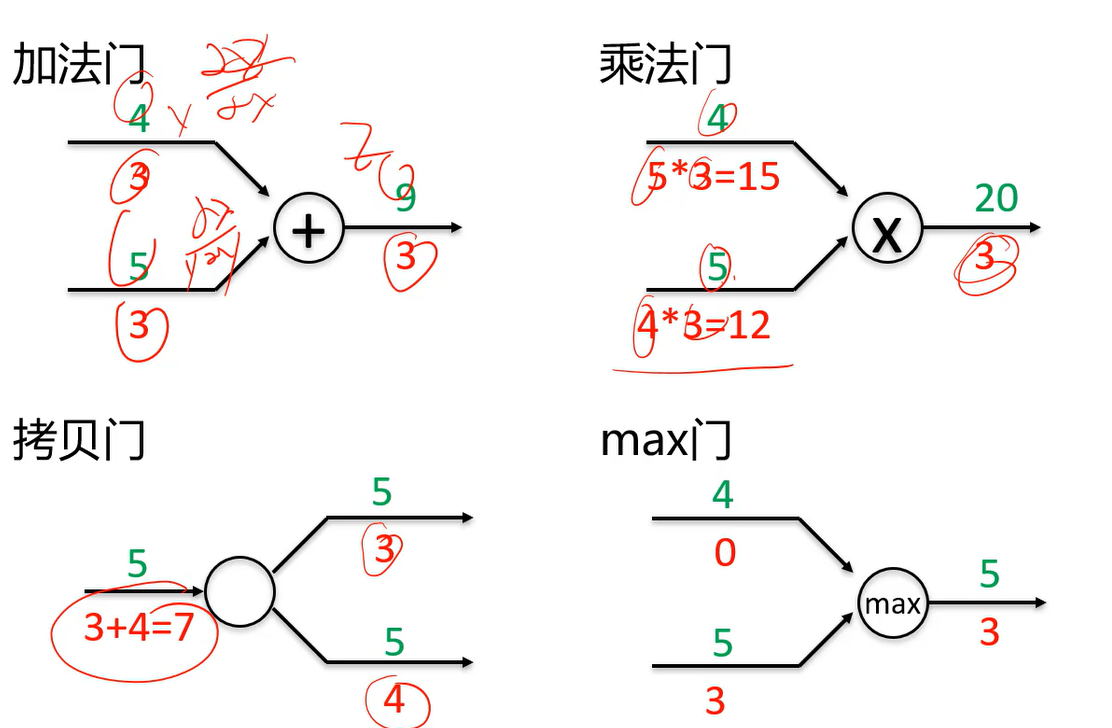
拷贝门（一个神经元输出多个结果给多人用），一个数据拷贝成两份，回传时，两路的信息要累加起来。
max门，哪个输入大，梯度就回传给谁。
再谈激活函数
梯度消失
- 梯度消失是神经网络训练中非常致命的一个问题，其本质是由于链式法则的乘法特性导致的。
- 一旦梯度消失，前面神经网络的参数就改变不了了。
- sigmoid函数大部分时候都是很小的梯度，接近0，最大的时候也才1/4，比如串10个，每次缩小1/4，几次以后梯度也消失了。因此现在sigmoid不再使用。
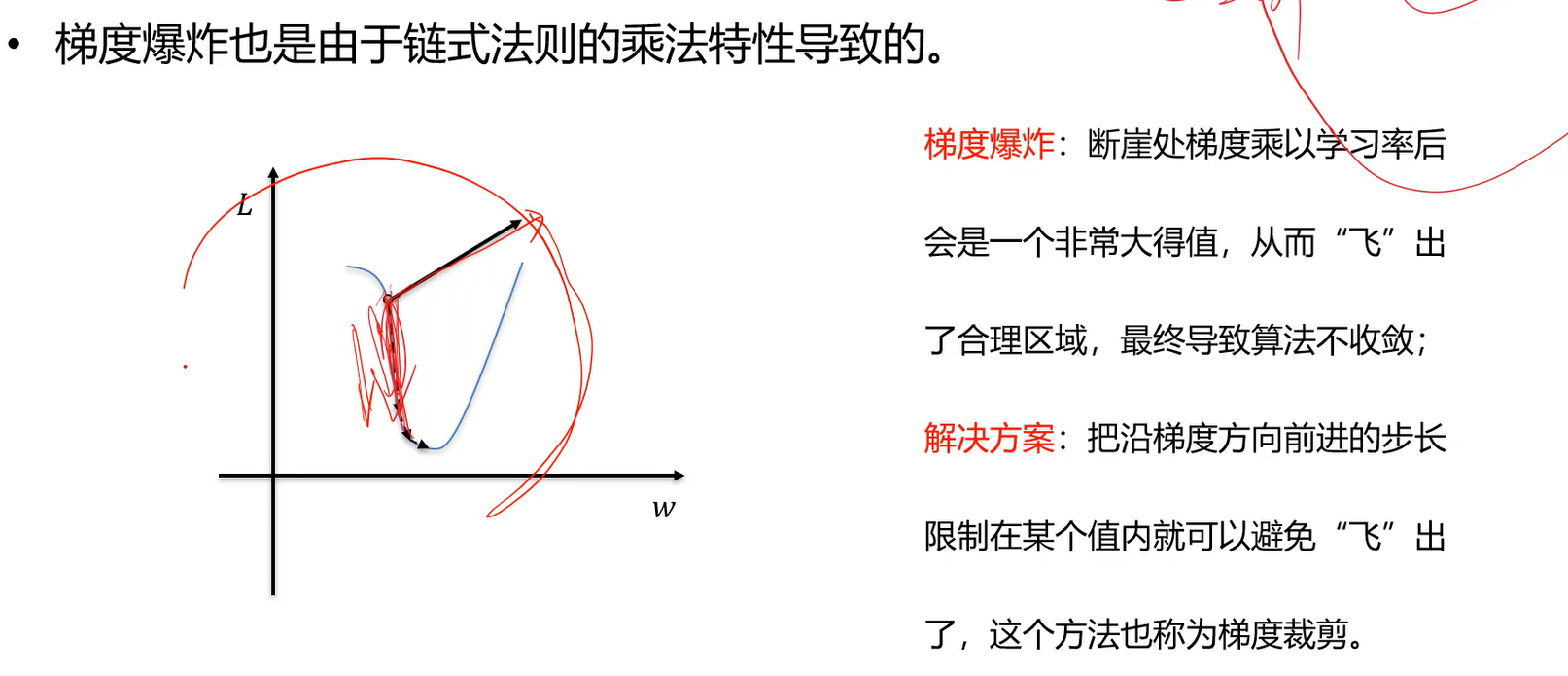
- 梯度爆炸，也是由于链式法则的乘法特性导致的。
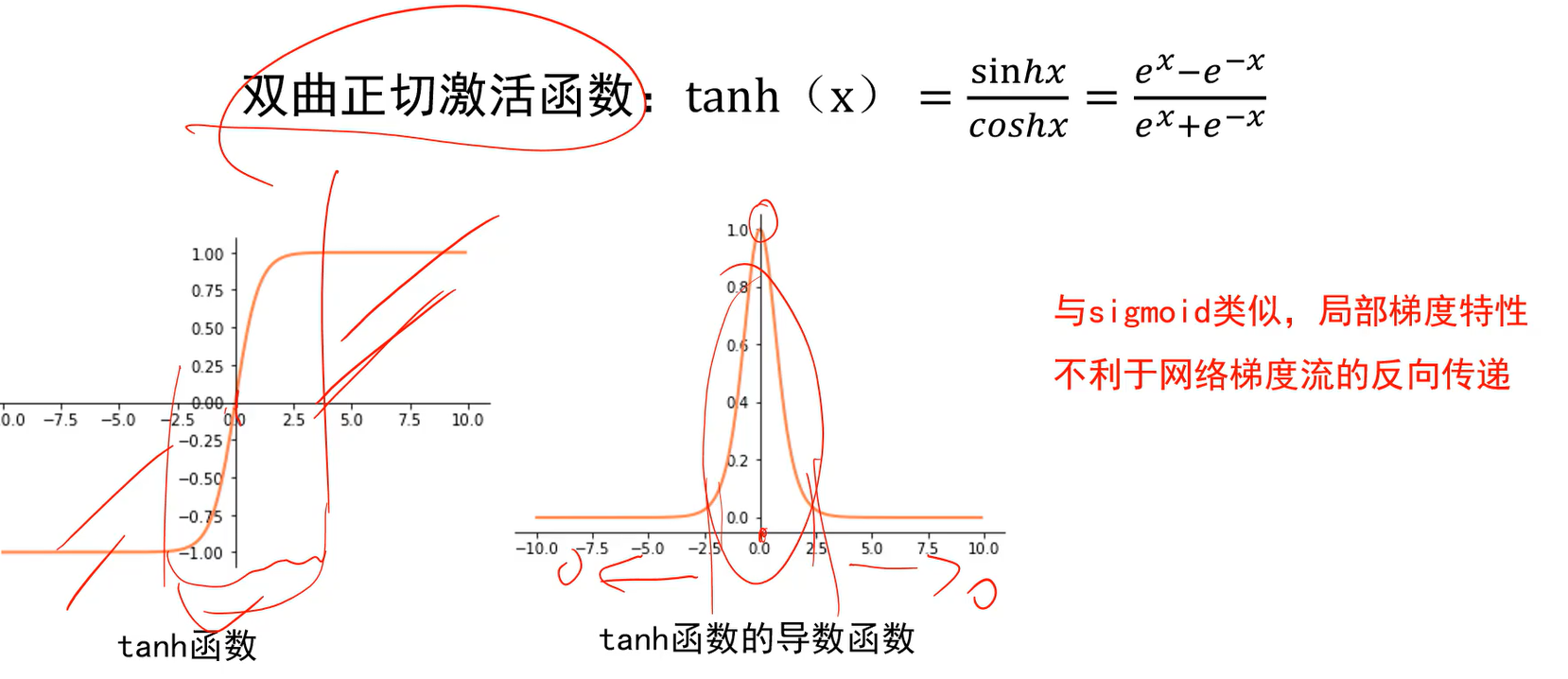
- 作为输出层，比如希望输出为0到1之间。可能会用到sigmoid或tanh。但作为隐层不会使用，因为局部梯度特性不利于网络梯度的传递。
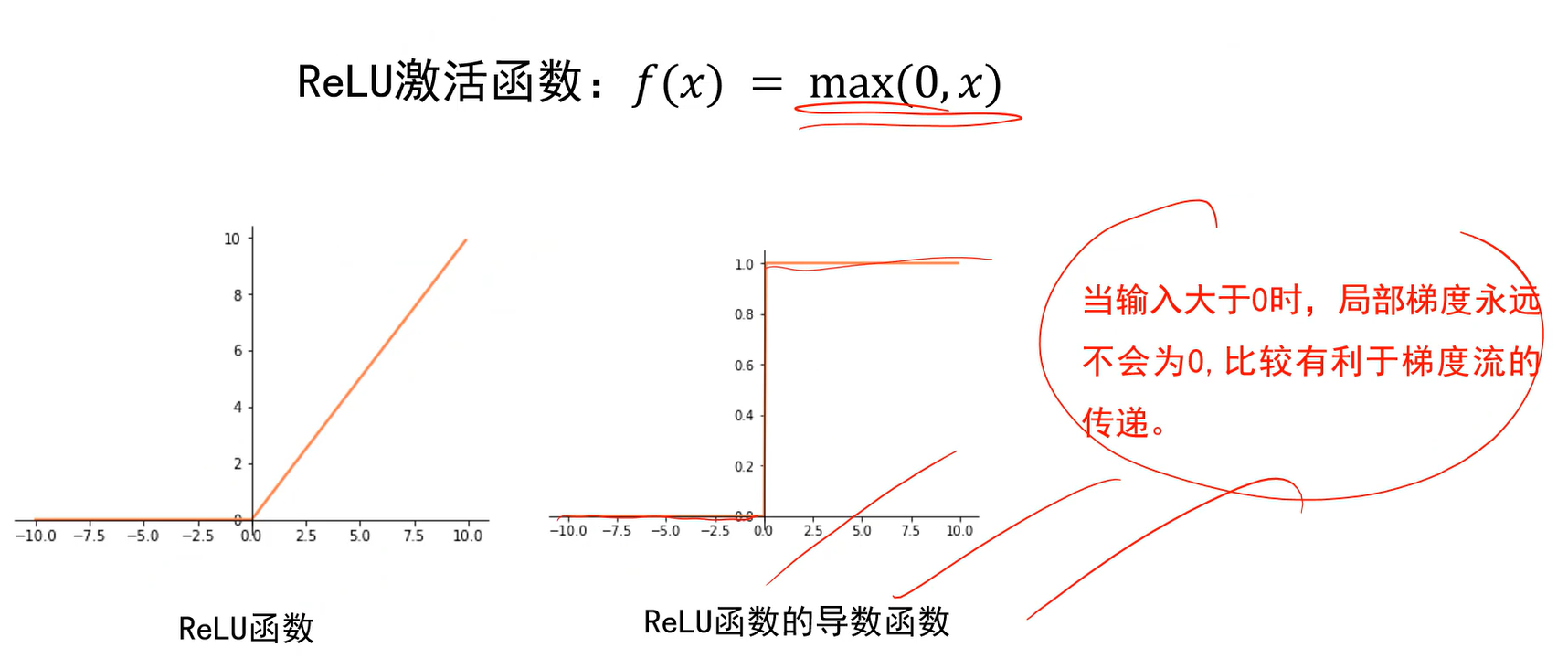
- 而relu函数，计算更简单（不用算指数），局部特性也很好。
- 但有些缺点，输入小于0时梯度为0。
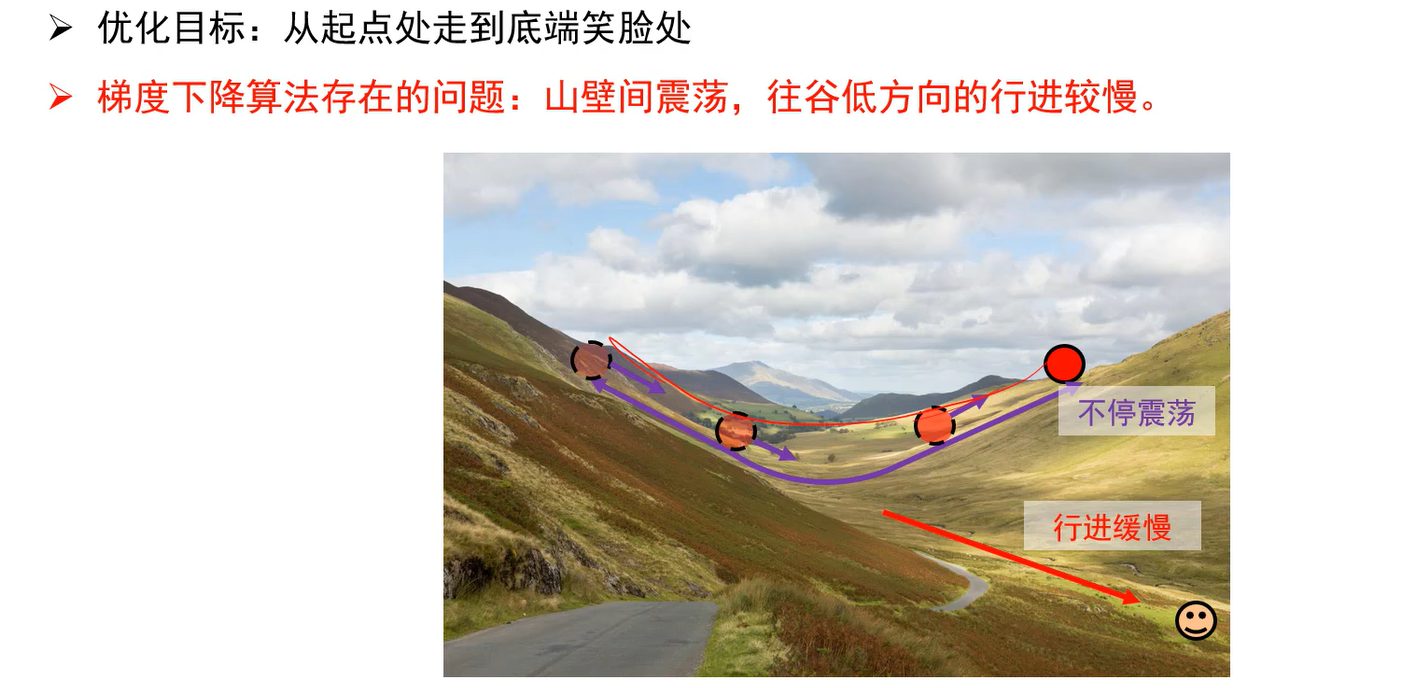
Q：为什么有效？
A：累加过程中震荡方向相互抵消，平坦方向得到加强。
\mu为何不取1，v=v+g，这样的话即使梯度下降算法走到平坦区域，g=0了，然而累加值v不为0，仍然会一直走，梯度下降算法就停止不了；而\mu为0.9的话，v=0.9v，相当于加了个摩擦系数，算法慢慢会停下来。
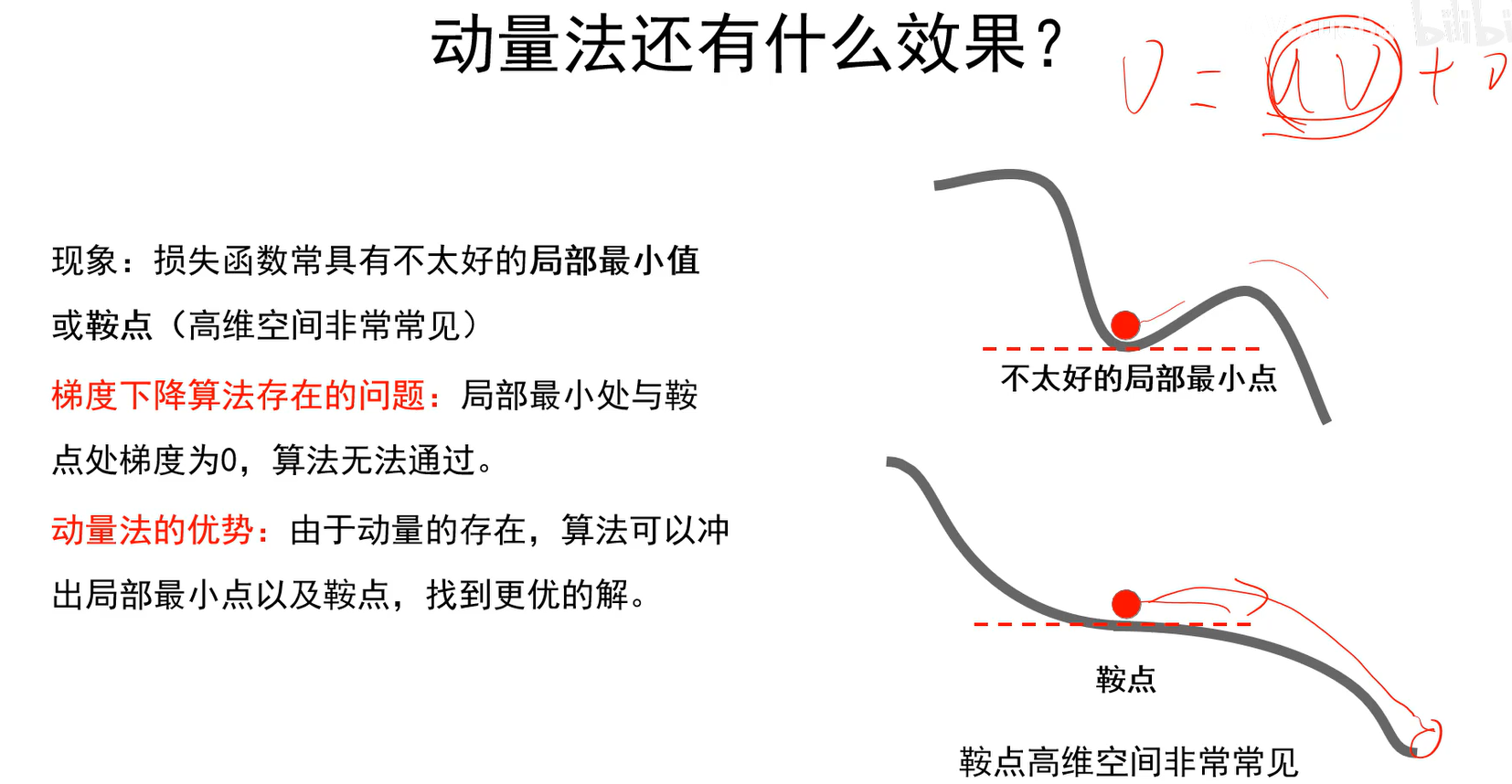
Q：如何区分震荡方向和平坦方向？
A：梯度幅度的平方较大的方向是震荡方向；幅度较小的方向是平坦方向。
写成代码的方式如下：
:::info
其实是自适应的调节学习率
:::
缺陷是，累加时间过长时，r会是个很大的值，此时学习率即真实的步长就会很小，就失去了调节的意义了。 因此下面讲解一种改进方法。
RMSProp
- 做法：每次的历史梯度加上一个衰减值。
- 好处：
- 当
为0时，仅靠当前梯度，当前梯度很大，就把此方向速度降慢；当前梯度小，就把此方向速度增大。 - 当为1时，就不考虑当前梯度了，因此不会取1.
- 一般设个0.999，非常接近1的值。如果梯度老是0，虽然为0.999，但求出的r会被一直衰减。因为每次乘0.999，连乘下去会是很小的值了，就不会再去影响梯度了。
- 增大代表着考虑的历史值越多。保留的历史次数越多，的值就要设置越大。打个比方，比如我要保留100次历史，可能就设为0.99。
:::info
自适应梯度即不同方向迈不同的步长来实现的。
:::
Adam
既然上面两种都是来解决这个问题，为何不结合在一起呢？这就是Adam，同时使用动量和自适应的思想。
:::info
修正项仅在训练初期，冷启动时起作用，来防止初期优化得很慢。t为训练轮次，当训练轮次变多时，
越来越小，
就越来越接近1，修正项就不起作用了。
:::
总结
推荐使用：
1、SGD+动量法
2、或直接用Adam。
但是SGD+动量法，调优的效果更好，手动调这两个东西的学习率会比Adam更好，但手动调到一个很优的值不太容易，这就是所谓的炼丹，炼丹很多时候就是在调这个东西。
Adam在很多任务下很快就能弄好。
很多时候我们使用Adam初始学习一下，学不动的时候用SGD+动量法手动调；也有时SGD+动量法先学一学，之后用Adam做后面的加速。
- 当
训练过程
权值初始化
训练的时候，总得给个权值来前向求解，然后才能反向计算梯度。即梯度下降时总要先给个起始点，起始点怎么给即权值初始化的问题。
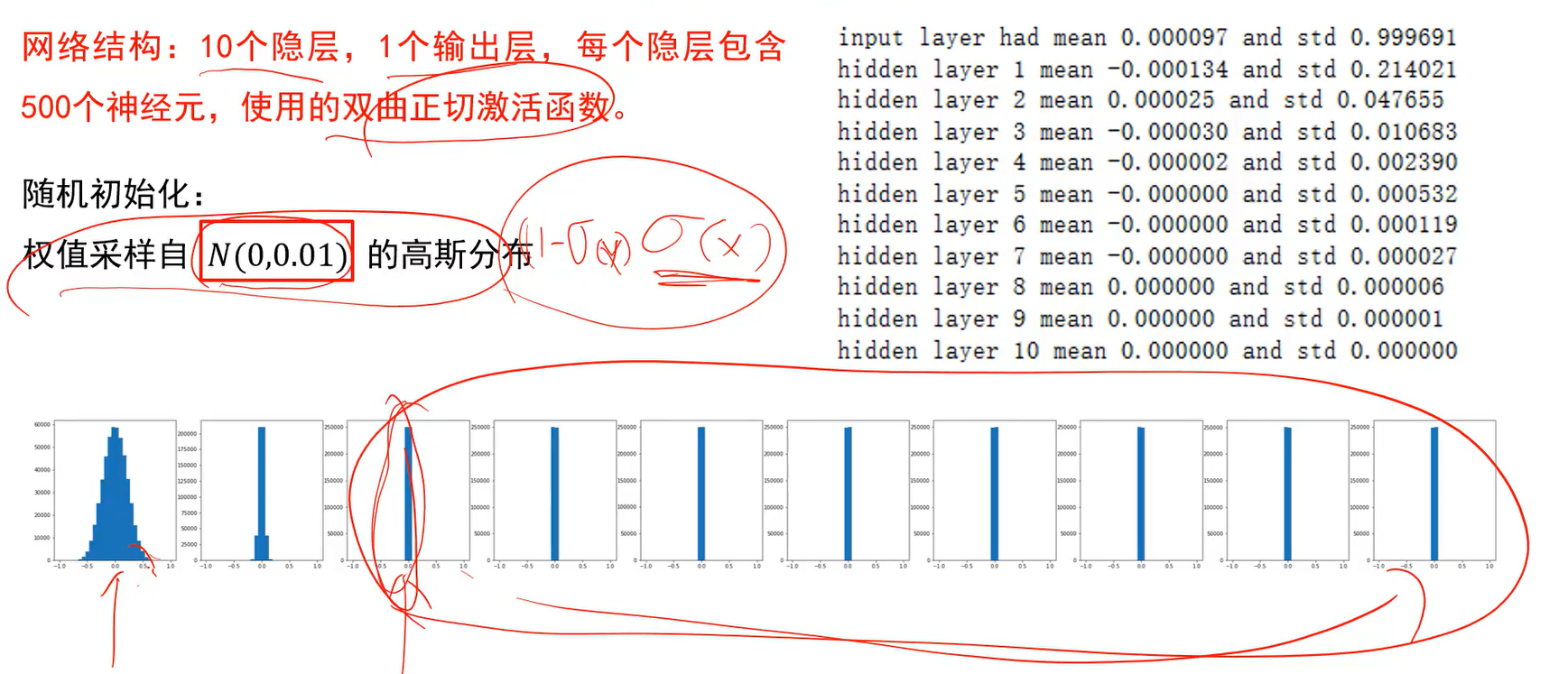
建议采用随机初始化，避免全零初始化。
如上图，采样自方差为0.1的高斯分布，输出值为0，则局部梯度也为0；后面的层，输出值为0，则输入的信息，根本就传不到输出。证明前向计算流都不畅通，反向梯度流也不可能畅通，网络无法被训练。
- 因此随机初始化如果初始化太小，前向传递就会被衰减。
的高斯分布。至少每层计算出的结果不一样，传回来的梯度也不一样，更新的值也不一样了；至少保证更新不是相同的。
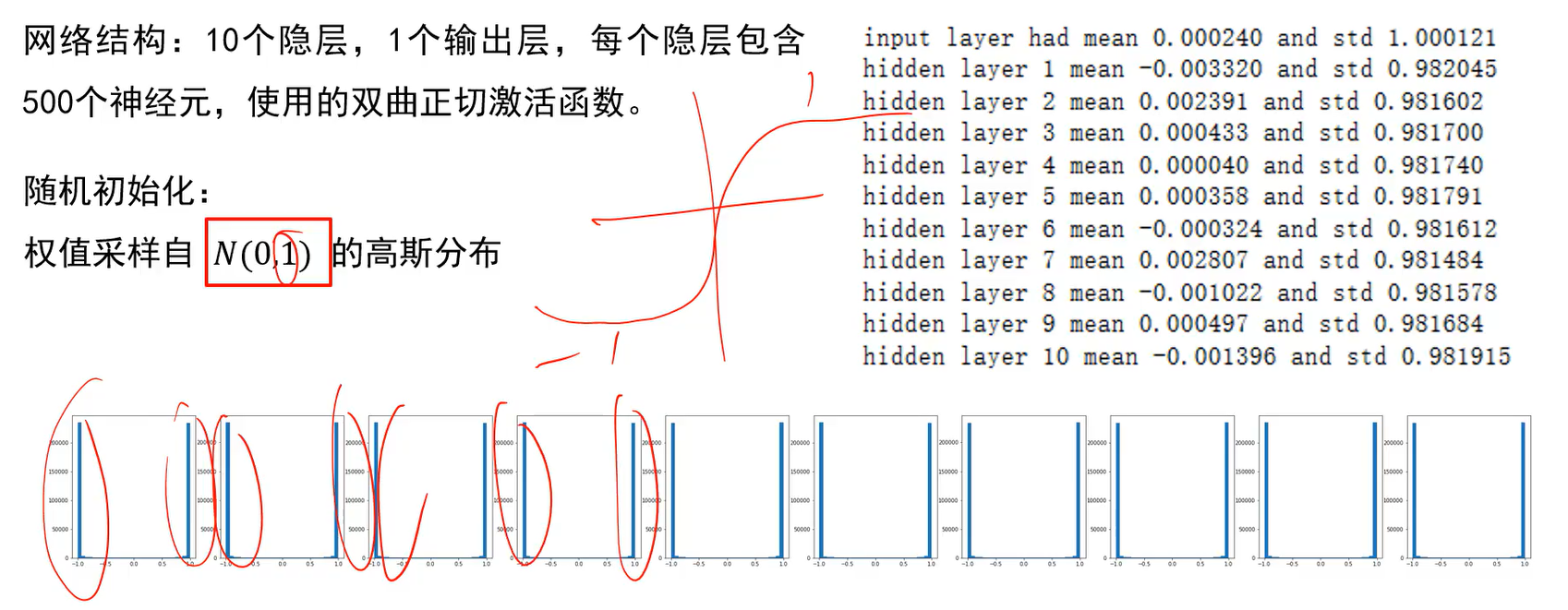
- 那如果采样自方差为1的高斯分布呢？如上图。-1到1时tanh函数的梯度进入饱和区，梯度就传不回来，网络还是无法训练。
结论：
目标是希望输出的y和输入的z有相同的分布，这样迭代过程中信息会正常的流动，反向梯度流也会正常。
如上图，每层输出值的分布不再是0附近，基本符合正态分布了，这样前向输出流就比较均匀，反向梯度也可以计算了。
HE初始化
对于ReLU激活函数来说，Xavier初始化方法仍然不好。
因此引入何凯明推出的方法。
权值初始化小结
好的初始化方法可以防止前向传播过程中的信息消失，也可以解决反向传递过程中的梯度消失。 :::info 当激活函数选择双曲正切或sigmoid时，建议适用Xavier初始化；
激活函数选择ReLU或leaky relu时，推荐使用He初始化方法 :::批归一化（Batch Normalization）
批归一化考虑问题的角度和权值初始化不一样。
批归一化与梯度消失
- 批归一化也称为BN操作，经常插入到全连接层后，非线性激活前。
- 解决两个问题：
- 正向传递时能保证每一层有数据往前传，不至于小到0。
- 反向传递问题，让数据都在激活函数梯度最有效的范围。
批归一化实现算法
- 批归一化算法除了归一化外，最后还加了一步平移缩放。
算法中的输入即原来神经网络的输出，算法的输出即经过批归一化算法的输出。m是批量。 多了两个参数，
是希望数据映射到新方差上去，
是希望数据映射到新均值上去。这两个参数也是神经网络学习的，并非超参。
这样输出的y就对应到神经网络自己选择的均值和方差。
Q：训练的时候是有批量的，测试的时候均值和方差怎么设置（测试时只有一个样本）？
A：来自于训练中。累加训练时每个批次的均值和方差，最后进行平均，用平均后的结果作为预测时的均值和方差。
:::info
批归一化和权值初始化要解决的问题，都是让我的信息流正向传递通常，反向传递也顺畅，这样才能保证网络能得到正常的训练。
:::
过拟合与欠拟合
出现过拟合，得到的模型在训练集上的准确率很高，但在真实场景中识别率很低。
:::info
之前学过，此部分没做笔记
:::
应对过拟合
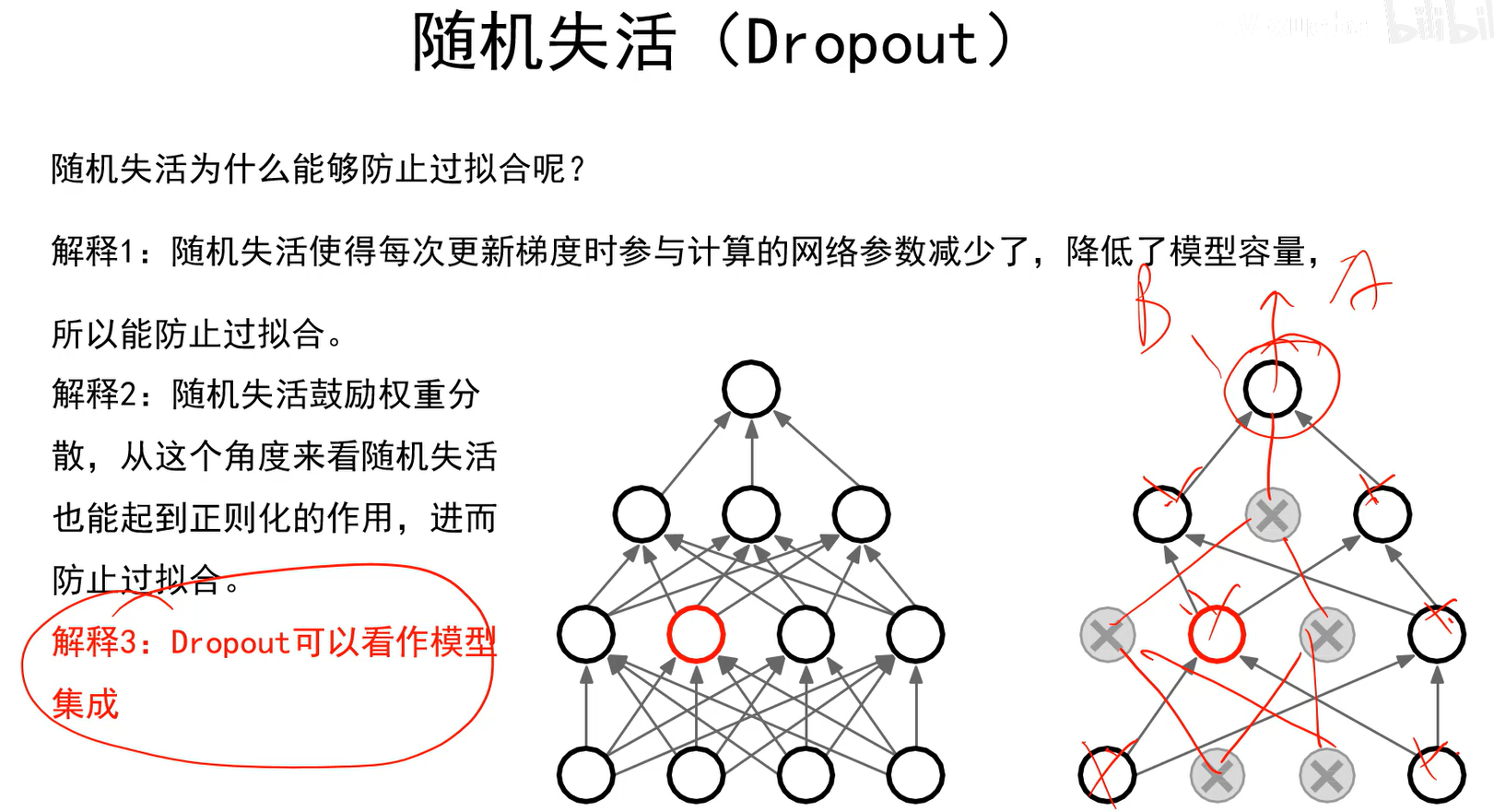
随机失活的应用
上图可以看出，因为随机失活在测试阶段是不用的，所有神经元都会打开，就会导致训练阶段的输出和测试阶段的输出范围之间差着1/2倍。
因此要给测试阶段的输出乘上p后，两个阶段的输出范围才是一样的，神经网络才能正常工作。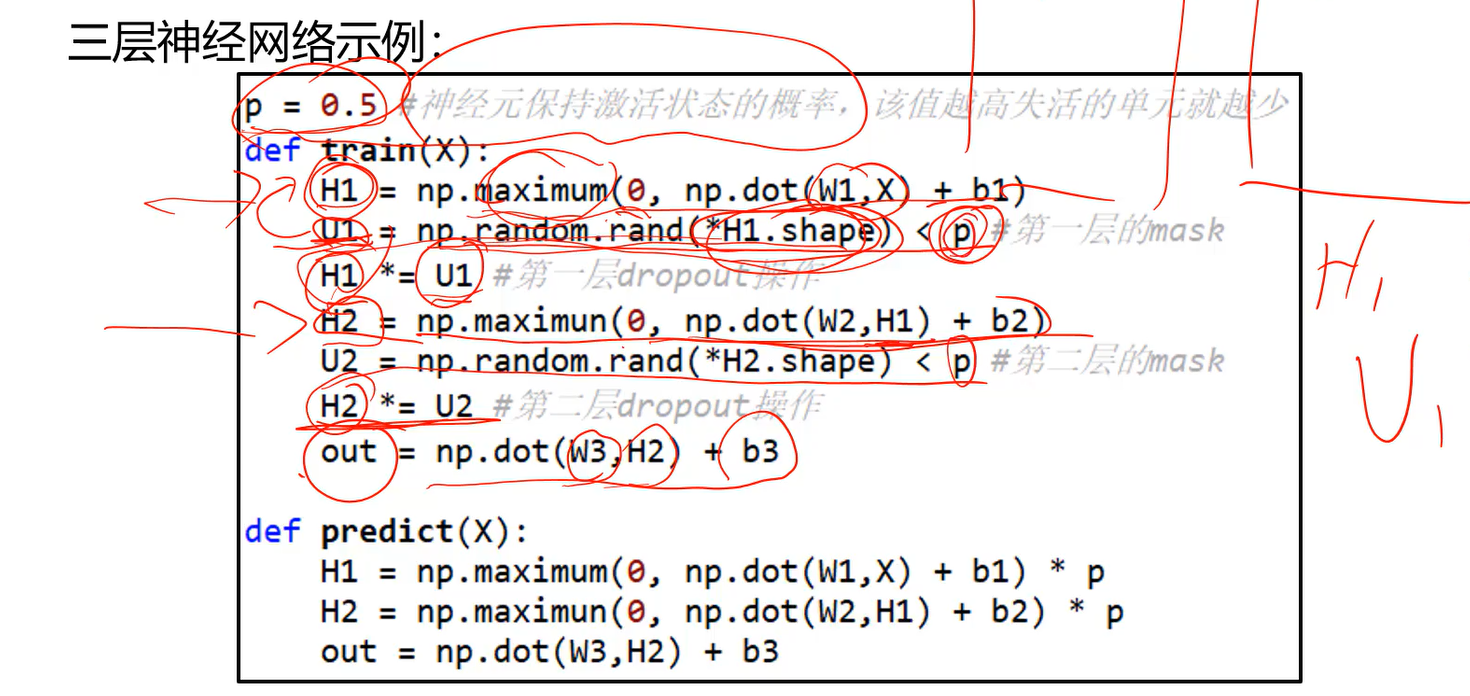
mask矩阵U里的元素非0即1。 测试阶段时，如果后面不乘p，则H输出的值，与训练阶段的H值就不一样了；因此预测时乘以p才能保证与训练时的输出一样。
- 真实应用中这样写起代码来不太方便，我们更希望随机失活作为一个层，希望这个层我加到H1后预测的时候不用再考虑它。
- 因此在U1后面除掉p。这样在训练阶段的输出就和真实预测的输出一样了。
- 这样就可以将U1当作一个层，即Dropout层。
- 输入H1，输出是随机失活处理后的H1，这个层只有一个参数p。
模型正则与超参数调优
若有收获，就点个赞吧
0 人点赞
