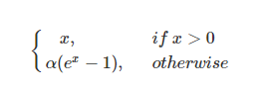梯度消失/爆炸

参考：详解深度学习中的梯度消失、爆炸原因及其解决方法；梯度消失和梯度爆炸及解决方案 :::info

• tldr：

  • 梯度消散和梯度爆炸本质上是一样的，都是因为网络层数太深而引发的梯度反向传播中的连乘效应。Sigmoid激活函数最容易产生梯度消散，这是由于它的函数特性决定的。
  • 如果使用Sigmoid作为激活函数，那么其梯度不可能超过0.25，当层数叠加，经过链式求导后。很容易产生梯度消失。 :::

    梯度消失/爆炸 原因分析

• 存在梯度消失和梯度爆炸问题的根本原因就是我们在深度神网络中利用反向传播的思想来进行权重的更新。即根据损失函数计算出的误差，然后通过梯度反向传播来减小误差、更新权重。

我们假设，存在一个如图所示的简单神经网络，我们可以得到相关的公式如右侧所示：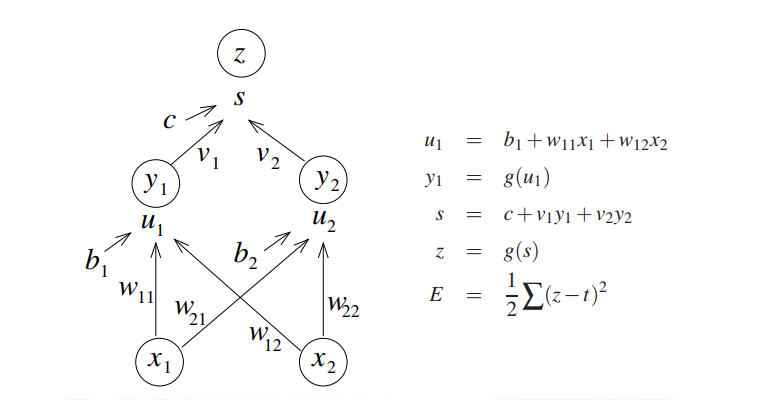

• 我们利用上面提到的公式来说明梯度消失产生的原因，求代价函数对 w11的偏导数，根据链式求导法则可以得到：

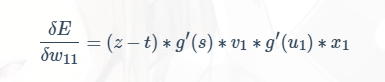
• 而我们神经网络中的初始权值也一般是小于 1 的数，所以相当于公式中是多个小于 1 的数在不断的相乘，导致乘积和还很小。这只是有两层的时候，如果层数不断增多，乘积和会越来越趋近于 0，以至于当层数过多的时候，最底层的梯度会趋近于 0，无法进行更新，并且 Sigmoid 函数也会因为初始权值过小而趋近于 0，导致斜率趋近于 0，也导致了无法更新。
• 除了这个情况以外，还有一个情况会产生梯度消失的问题，即当我们的权重设置的过大时候，较高的层的激活函数会产生饱和现象，如果利用 Sigmoid 函数可能会无限趋近于 1，这个时候斜率接近 0，最终计算的梯度一样也会接近 0， 最终导致无法更新。 :::info 总结：

• 根据链式求导法则，对输入层求梯度时，中间会乘上激活函数的导数，如果激活函数是sigmoid，很容易落到饱和区，梯度为0或者梯度小于1，经过不断连乘，梯度越来越小，反向传播到前面的层时就会趋于0，所以梯度消失。

• 从上面的公式还能得到一点：

  • v1即第二层的权重，也可写作w2，即代价函数对w11的偏导数中，除了要乘激活函数的导数外，还要乘中间层的权重。
  • 因此除了激活函数导数落入饱和区导致的梯度消失外，还有可能因为中间层权重过大导致的梯度消失或爆炸，因此对应的有权重正则、bn等解决方案。 :::
    

    可能额出现梯度消失/爆炸的情况

• 梯度消失经常出现的情况：

  • 深层网络中
  • 采用了不合适的激活函数，如sigmoid

• 梯度爆炸经常出现的情况

  • 深层网络中
  • 权重初始化值太大

    深层网络角度

    从深层网络角度来讲，不同的层学习的速度差异很大，表现为网络中靠近输出的层学习的情况很好，靠近输入的层学习的很慢，有时甚至训练了很久，前几层的权值和刚开始随机初始化的值差不多。因此，梯度消失、爆炸，其根本原因在于反向传播训练法则，本质在于方法问题

    激活函数角度

• 上文中提到计算权值更新信息的时候需要计算前层偏导信息，因此如果激活函数选择不合适，比如使用sigmoid，梯度消失就会很明显了，原因看下图，左图是sigmoid的损失函数图，右边是其倒数的图像，如果使用sigmoid作为损失函数，其梯度是不可能超过0.25的，这样经过链式求导之后，很容易发生梯度消失，sigmoid函数数学表达式为：

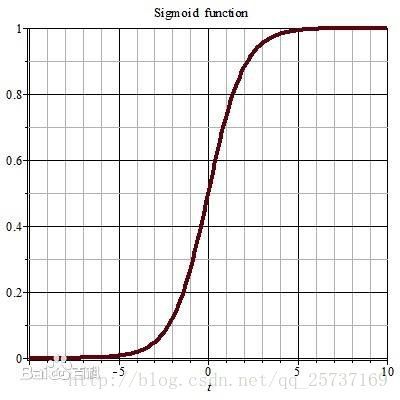
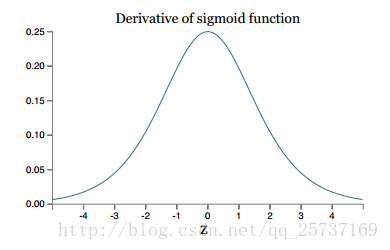
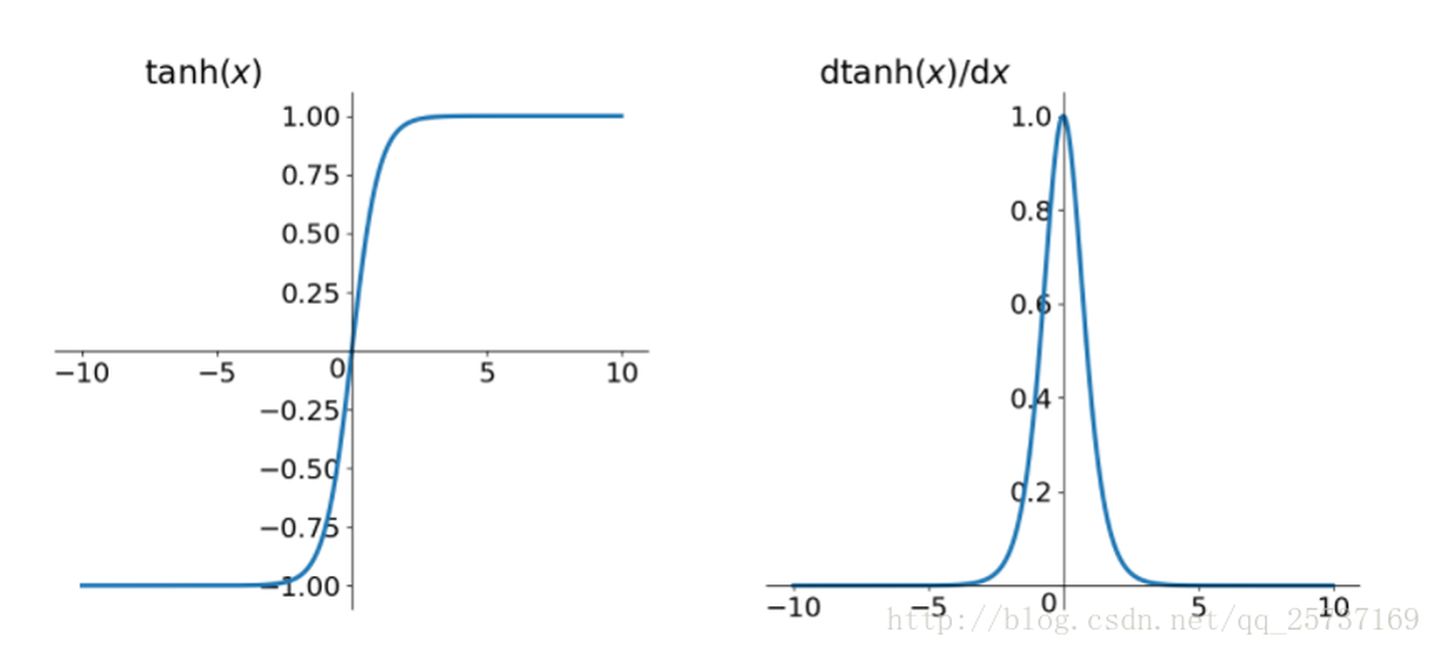
• 同理，tanh作为损失函数，它的导数图如下，可以看出，tanh比sigmoid要好一些，但是它的倒数仍然是小于1的。tanh数学表达为：

缓解s方案

1、梯度剪切

其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。

注：在WGAN中也有梯度剪切限制操作，但是和这个是不一样的，WGAN限制梯度更新信息是为了保证lipchitz条件。

2、权重正则化

采用权重正则化（weithts regularization）比较常见的是l1正则，和l2正则，在各个深度框架中都有相应的API可以使用正则化。
正则化是通过对网络权重做正则限制过拟合，仔细看正则项在损失函数的形式：

其中， 是指正则项系数，因此，如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。 :::info 注：事实上，在深度神经网络中，往往是梯度消失出现的更多一些 :::

3、采用relu，leaky-relu，elu等激活函数

• ReLu:思想也很简单，如果激活函数的导数为1，那么就不存在梯度消失爆炸的问题了，每层的网络都可以得到相同的更新速度，relu就这样应运而生。

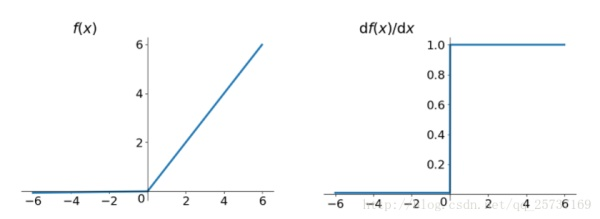
• relu的主要贡献在于：
  • 解决了梯度消失、爆炸的问题
  • 计算方便，计算速度快
  • 加速了网络的训练
• 同时也存在一些缺点：
  • 由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）
  • 输出不是以0为中心的

Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。

• Leaky-ReLu：leakrelu就是为了解决relu的0区间带来的影响，

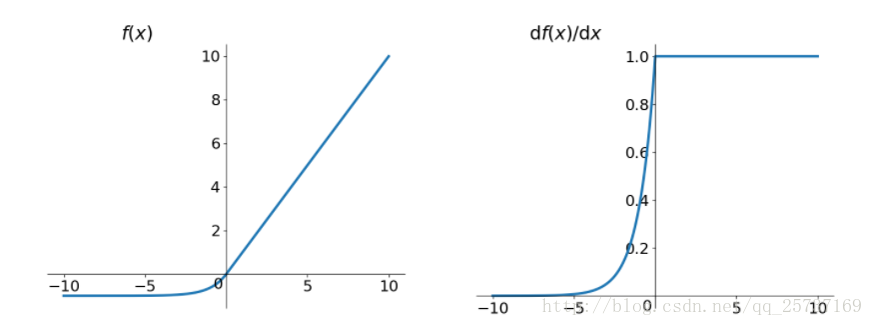
• elu：elu激活函数也是为了解决relu的0区间带来的影响，但是elu相对于leakrelu来说，计算要更耗时间一些。

4、batch norm

通过规范化操作将输出信号x规范化到均值为0，方差为1保证网络的稳定性。
具体的batchnorm原理非常复杂，在这里不做详细展开，此部分大概讲一下batchnorm解决梯度的问题上。具体来说就是反向传播中，经过每一层的梯度会乘以该层的权重，举个简单例子： 正向传播中 ，那么反向传播中， ，反向传播式子中有w的存在，所以 的大小影响了梯度的消失和爆炸，batchnorm就是通过对每一层的输出做scale和shift的方法，通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到接近均值为0方差为1的标准正太分布，即严重偏离的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，使得让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

Q：这里有个问题，为何会出现f2对x的偏导？不应该是对w求导嘛 A：比如若要对i层w求导，因为第i+1层的输入x需要通过i层的w计算得来，所以反向传播也需要对x求导。 总的来说，关于影响第i层梯度的因素，我认为包括：i和之后层的激活函数的导数，i+1和之后层的w，以及i层的输入。 可以试一下三层网络反向传播求导，x视为是上一层网络的输出x=f(x0)=w*x0，计算前层参数更新的时，根据链式求导法则是要对x求导的。

5、残差结构

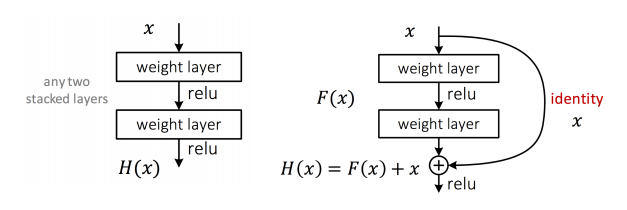
• F(x)F(x) 被称为一个 residual component，主要是纠正以前层的错误或者提供前一层计算不出的额外的细节
• 如果超过了 100 层需要在添加残差之前就使用 ReLU 而不是之后。这个过程被叫做 identity skip connection

短路机制可以无损地传播梯度。