知乎：如何通俗的解释交叉熵与相对熵？
image.png
交叉熵/相对熵 - 图2

最大化似然函数与最小化交叉熵

贝努力分布（两点分布）

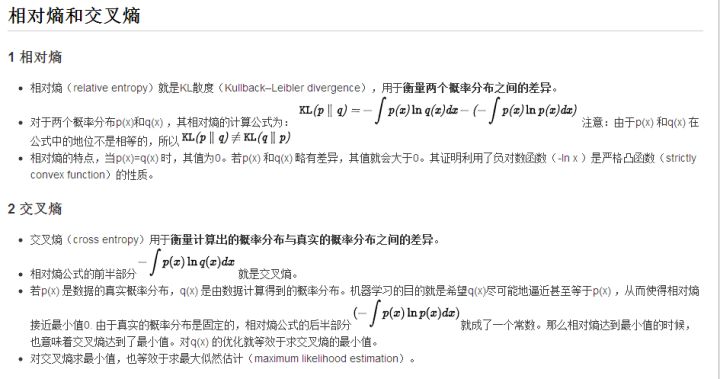
贝努利分布可以看成是将一枚硬币（只有正反两个面，代表两个类别）向上扔出，出现某个面（类别）的概率情况，因此其概率密度函数为：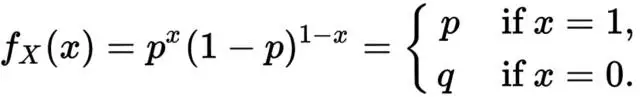
交叉熵/相对熵 - 图3
贝努利分布的模型参数就是其中一个类别的发生概率。

二项分布

就是将贝努利实验重复n次（各次实验之间是相互独立的）。

单次观测下的多项式分布

单次观测下的多项式分布就是贝努利分布的多类推广：
交叉熵/相对熵 - 图4
其中，C代表类别数。p代表向量形式的模型参数，即各个类别的发生概率，如p=[0.1, 0.1, 0.7, 0.1]，则p1=0.1, p3=0.7等。即，多项式分布的模型参数就是各个类别的发生概率！x代表one-hot形式的观测值，如x=类别3，则x=[0, 0, 1, 0]。xi代表x的第i个元素，比如x=类别3时，x1=0，x2=0，x3=1，x4=0。

总结

  • 对于多类分类问题，似然函数就是衡量当前这个以predict为参数的单次观测下的多项式分布模型与样本值label之间的似然度。
  • 根据似然函数的定义，单个样本的似然函数即：交叉熵/相对熵 - 图5
  • 整个样本集（或者一个batch）的似然函数即：交叉熵/相对熵 - 图6

由于式子里有累乘运算，所以加个log来转化为累加来提高计算速度，即得到对数似然函数。而最大化对数似然函数就等效于最小化负对数似然函数。而这个形式跟交叉熵的形式是一模一样的：

  • 对于某种分布的随机变量X~p(x), 有一个模型q(x)用于近似p(x)的概率分布，则分布X与模型q之间的交叉熵即：

交叉熵/相对熵 - 图7

  • 真实分布为one-hot形式时，交叉熵损失简化为：交叉熵/相对熵 - 图8。 :::info 实际用于分类问题时，还要进行softmax，即还要除以分母。
    交叉熵/相对熵 - 图9
    因此，要想交叉熵损失小，不仅要求预测分数高，同时要要求其他类别预测分数低，这样去取softmax时，分子占分母的比例就会变大，即log里面的数字大，损失就会变小。 :::

    为何分类问题中使用交叉熵

    为什么分类模型 Loss 函数要用 交叉熵Cross Entropy?
    为何不用Classification Error比如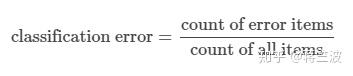：image.png
    因为交叉熵能更清晰地描述模型与理想模型的距离，且交叉熵计算loss是一个凸优化问题。

    交叉熵损失 vs. 多类支撑向量机损失

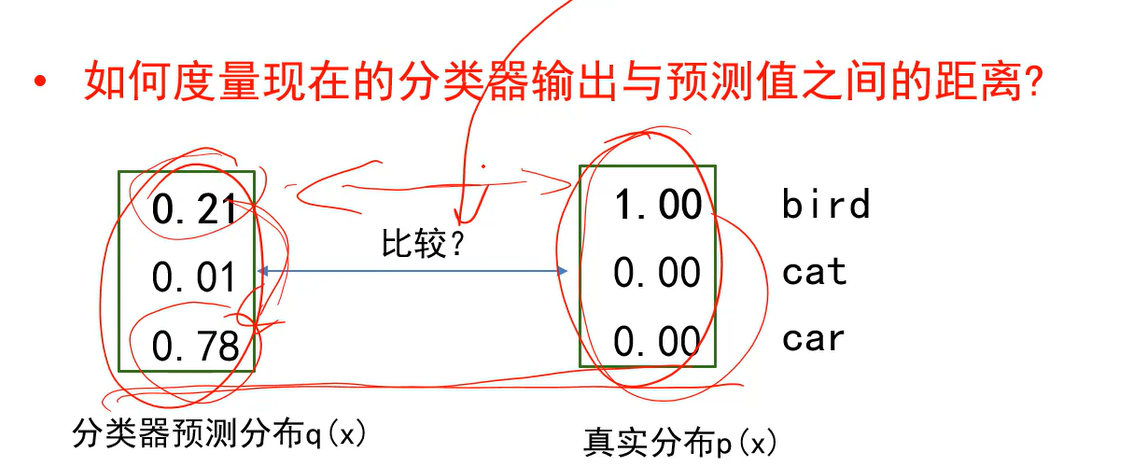
    image.png

  • 交叉熵能够衡量分类器预测分布q(x)和真实分布p(x)之间的差异。当两个分布越接近时，交叉熵的损失值就越小。

  • 上述距离不能用多类支撑向量机损失来度量，因为它不考虑右侧，只考虑左侧比如车的答案和鸟的答案之间的关系，大过1没有。无法考虑两个概率分布之间的关系。

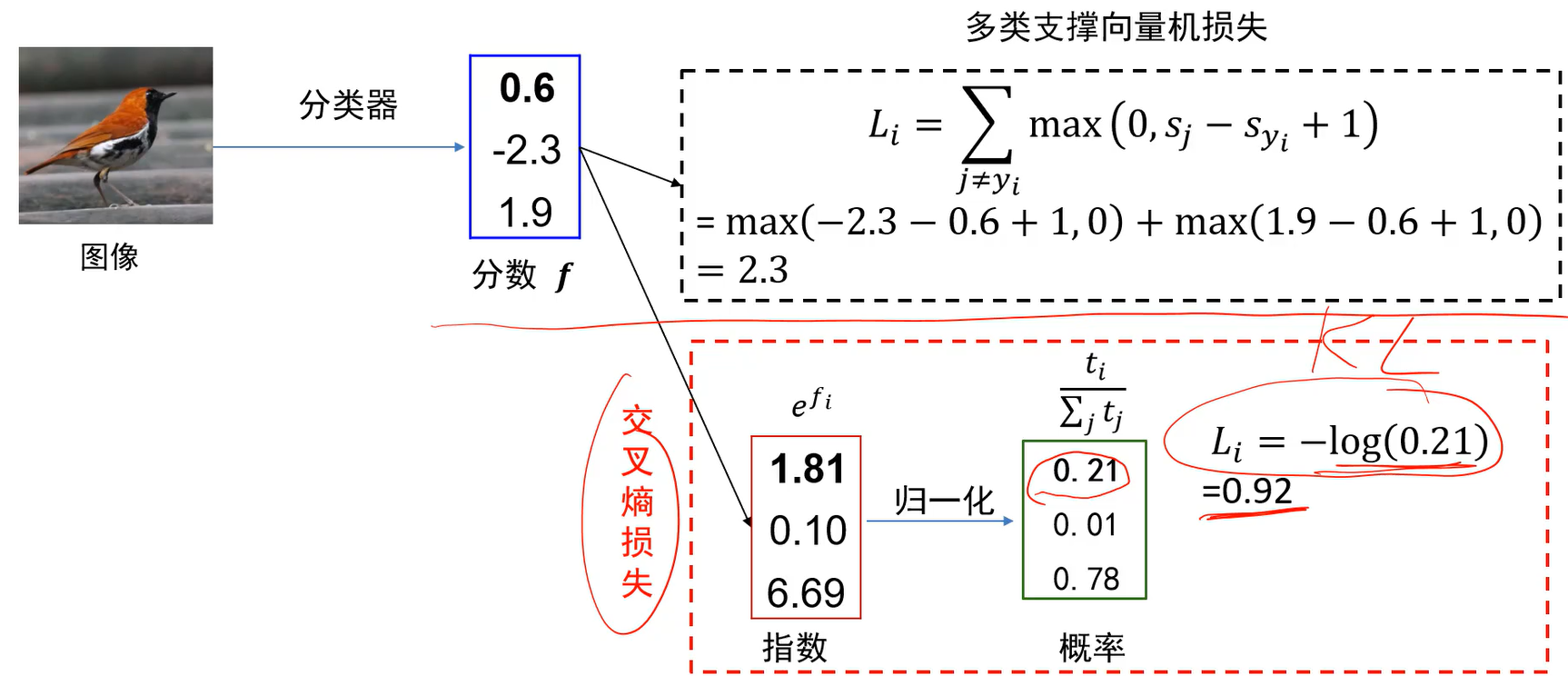
image.png
Q：相同分数下两种分类器的损失有什么区别？
A：交叉熵在下面第二种情况下并没有停止训练，因为不仅要求预测类别分数高，同时要求其他类别分数低。而多类支撑向量机损失只要比别人高1分就行了。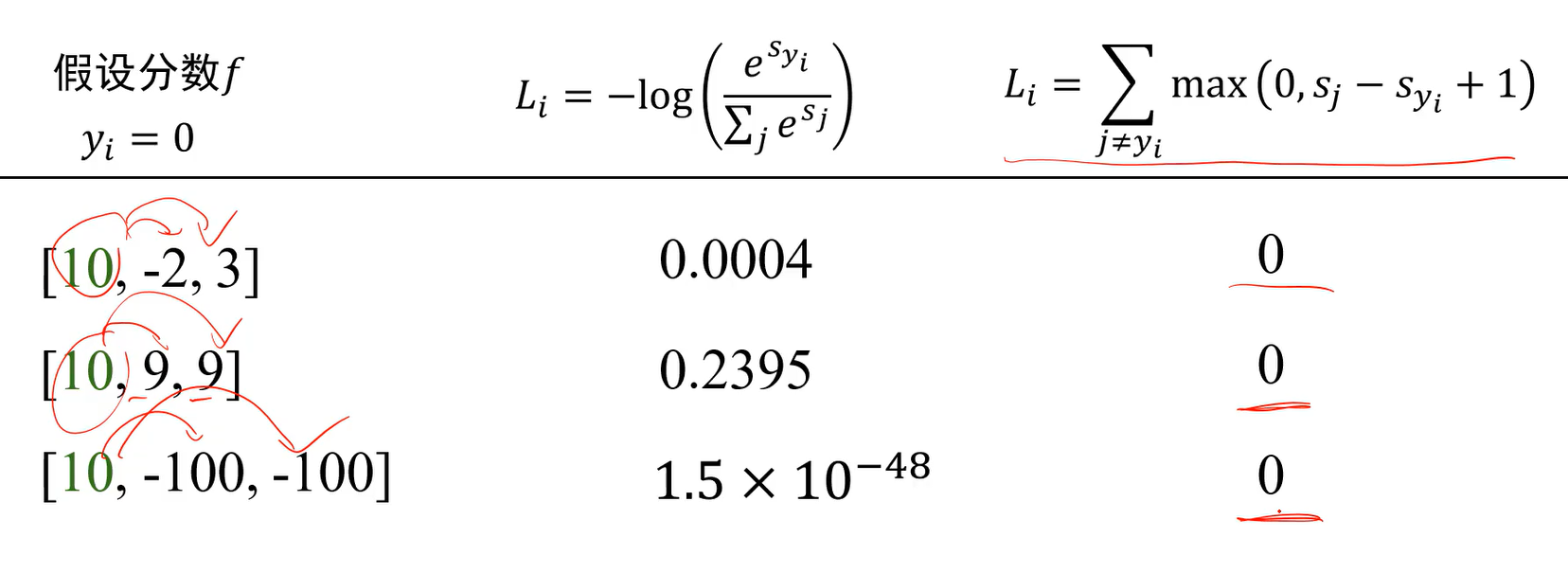
image.png

pytorch中的实现

另外，补充下pytorch中的实现，加深理解：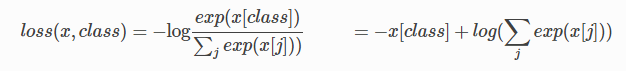
交叉熵/相对熵 - 图14
仔细看看公式，发现其实它就是nn.LogSoftmax() + nn.NLLLoss()

logSoftmax比softmax有更好的数值稳定性。

  • 可以看出要想让这个损失小，
    • 除了对应类别的预测值要大，对应公式中第一项的值大。
    • 还要让第二项的值小，即其他类别的预测值要小。 :::info 注意CrossEntropyLoss()的target输入也是类别值，不是one-hot编码格式 :::

Softmax输出及其反向传播求导

Softmax 输出及其反向传播推导；softmax相关知识总结

  • 符号含义：z是softmax的输入，y是softmax的输出，t是真实标签。

image.png

  • softmax函数的导数（即输出y对输入z的导数）
    • 对softmax求导数，就是求第i项的输出对第j项输入的导数。
    • 由于softmax有多个输出，因此会出现i和j，带入softmax表达式。
  • 由于softmax公式的特性。分母包含了所有神经元的输出，因此，上述求导过程要分情况讨论：
    • 如果 交叉熵/相对熵 - 图16，则 交叉熵/相对熵 - 图17 对 交叉熵/相对熵 - 图18 求导的结果为交叉熵/相对熵 - 图19;
    • 如果交叉熵/相对熵 - 图20 ，则 交叉熵/相对熵 - 图21 对 交叉熵/相对熵 - 图22 求导的结果为 0。

并且 交叉熵/相对熵 - 图23对 交叉熵/相对熵 - 图24 的求导结果总是 交叉熵/相对熵 - 图25 。
image.png

  • 交叉熵损失函数的梯度：即交叉熵损失函数交叉熵/相对熵 - 图27对输入z的导数。

image.png

倒数第五行，文中笔误，最后应该是乘“y_i*y_j” y_i即在第i个类别上的预测概率，t_i为label，最终只会有一个类别为1，其他的类别都是0.

  • MXNet上求softmax梯度的源码：
    1. template<typename DType>
    2. inline void SoftmaxGrad(Tensor<cpu, 2, DType> dst,
    3.                       const Tensor<cpu, 2, DType> &src,
    4.                       const Tensor<cpu, 1, DType> &label) {
    5. for (index_t y = 0; y < dst.size(0); ++y) {
    6.   const index_t k = static_cast<int>(label[y]);
    7.   for (index_t x = 0; x < dst.size(1); ++x) {
    8.     if (x == k) {
    9.       dst[y][k] = src[y][k] - 1.0f;
    10.     } else {
    11.       dst[y][x] = src[y][x];
    12.     }
    13.   }
    14. }
    15. }

    softmax和sigmoid/relu反向传播的区别

    参考：关于 Softmax 回归的反向传播求导数过程
    SoftmaxSoftmax 回归的激活部分，和使用 Sigmoid/ReLuSigmoid/ReLu 作为激活函数是有所不同的，因为在 Sigmoid/ReLuSigmoid/ReLu 中，每一个神经元计算得到 zz 后不需要将其它神经元的 zz 全部累加起来做概率的 归一化 ；也就是说以往的 Sigmoid/ReLuSigmoid/ReLu 作为激活函数，每一个神经元由 zz 计算 aa 时是独立于其它的神经元的；所以在反向传播求导数的时候，我们就能发现当计算 ∂a∂z∂a∂z 的时候，不再是单独的一一对应的关系，而是像正向传播那样，将上一层的结果全部集成到每一个神经元上，下面的图中，红色箭头表示了 SoftmaxSoftmax 和 Sigmoid/ReLuSigmoid/ReLu 的反向传播的路径的有所不同。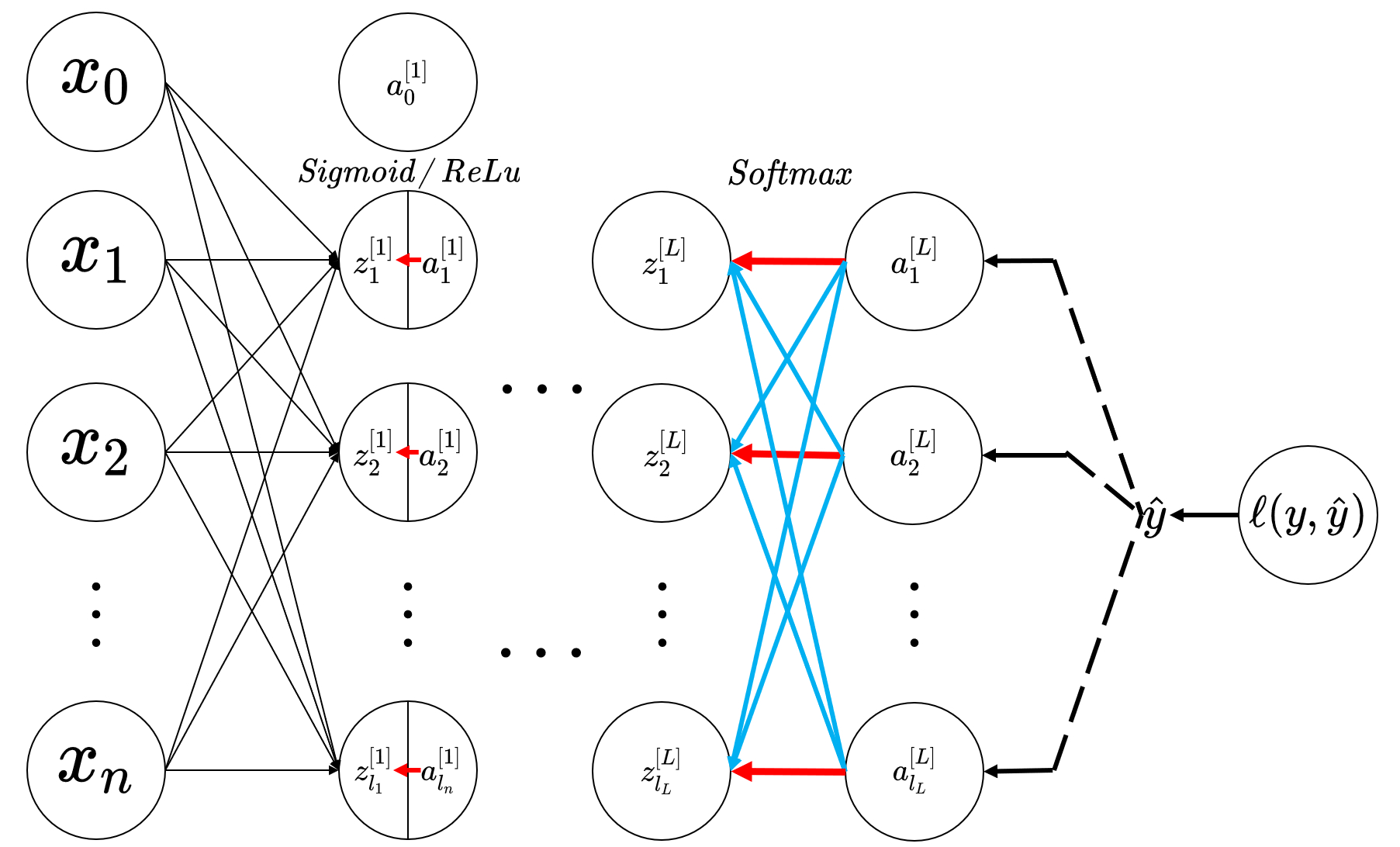
    交叉熵/相对熵 - 图29
    在上图中， SoftmaxSoftmax 层的激活的反向传播，可以看到每一个 a[L]iai[L] 都回馈到了不同的 z[L]jzj[L] 的神经元上；其中红色的线表示了 i=ji=j 的情况，其它蓝色的线表明了 i≠ji≠j 的情况，这也说明了为什么在 SoftmaxSoftmax 里的求导中会出现两种情况；反观第一层中的 Sigmoid/ReLuSigmoid/ReLu 激活中，每一个对 z[1]izi[1] 的激活都是在本地的神经元中得到的，没有其它神经单元传入的情况，所以也没有复杂的分下标 i,ji,j 讨论求导的情况。