注意力机制（Attention Mechanism）

参考来源：
知乎：NLP 中的 Attention 注意力机制 + Transformer 详解
Attention in Neural Networks and How to Use It
CSDN：神经网络的注意力机制（Attention）
知乎：神经网络中的注意力机制

1. 注意力的简介

注意力机制也称为：“神经网络的注意力”，或者更简单的：“注意力”。
人脑在工作时，其实是由一定的注意力的，比如我们在浏览器上搜索时，大部分的注意力都集中在搜索结果的左上角，这说明大脑在处理信号的时候是有一定权重划分的，而注意力机制的提出正是模仿了大脑的这种特性。
神经网络的注意力就是说，神经网络具有将注意力集中到一部分输入（或特征）的能力。

（1）为什么引入注意力机制呢？

根据通用近似定理，前馈网络和循环网络都有很强的能力。但为什么还要引入注意力机制呢？

• 计算能力的限制：目前计算能力依然是限制神经网络发展的瓶颈，当输入的信息过多时，模型也会变得更复杂，通过引入注意力，可以减少处理的信息量，从而减小需要的计算资源。
• 优化算法的限制：虽然局部连接、权重共享以及 pooling 等优化操作可以让神经网络变得简单一些，有效缓解模型复杂度和表达能力之间的矛盾；但是，如循环神经网络中的长序列输入，信息“记忆”能力并不高。

可以借助人脑处理信息过载的方式，例如 Attention 机制可以提高神经网络处理信息的能力。

（2）注意力机制的分类

当用神经网络来处理大量的输入信息时，也可以借鉴人脑的注意力机制，只选择一些关键的信息输入进行处理，来提高神经网络的效率。按照认知神经学中的注意力，可以总体上分为两类：

• 聚焦式（Focus）注意力：是一种自上而下的有意识的注意力，“主动注意” 是指有预定目的、依赖任务的、主动有意识地聚焦于某一对象的注意力；
• 显著性（Saliency-Based）注意力：是一种自下而上的无意识的注意力，“被动注意” 是基于显著性的注意力，是由外界刺激驱动的注意，不需要主动干预，也和任务无关；池化（Max Pooling） 和 门控（Gating）机制 也可以近似地看作是自下而上的基于显著性的注意力机制。

2. 注意力机制的流程

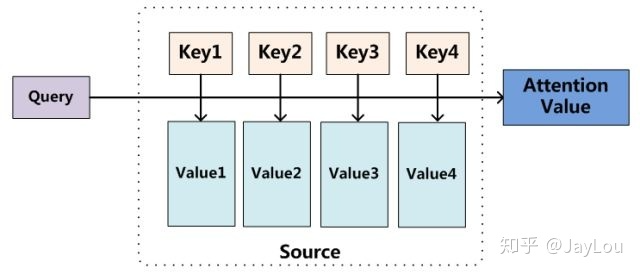
Attention机制的实质：寻址（addressing）

Attention机制的实质其实就是一个寻址（addressing）的过程，如上图所示：给定一个和任务相关的查询Query向量 q，通过计算与Key的注意力分布并附加在Value上，从而计算Attention Value，这个过程实际上是Attention机制缓解神经网络模型复杂度的体现：不需要将所有的N个输入信息都输入到神经网络进行计算，只需要从X中选择一些和任务相关的信息输入给神经网络。
注意力机制一般可以分为三步：一是信息输入；二是计算注意力分布；三是根据计算的注意力分布来对输入信息进行处理。
令：

• x ∈ R**d** 为输入向量。
• X = [x**1 , x2 , … , xN**] 为 N 个输入样本。
• q ∈ R**k** 为查询向量或特征向量。
• z ∈ [1,N] 为注意力变量，表示被选择信息的位置，比如 z=i 表示选择了第 i 个输入向量。

step1-信息输入

step1-信息输入：用 X = [x**1 , x2 , … , xN**] 表示 N 个输入信息；

step2-注意力分布计算

step2-注意力分布计算：令 Key=Value=X，则可以给出注意力分布：

我们将 α**i 称之为是注意力分布（概率分布）， s( xi , q ) 是注意力打分函数。
常见的注意力打分函数 s( xi , q )** 有：

• 加性模型：s(xi , q) = vT tanh(Wxi + Uq)；W、U 为可学习的网络参数。
• 点积模型：s(xi , q) = xiT q
• 缩放点积模型：s(xi , q) = (xiT q)/(d1/2) ；d 为输入向量的维度。
• 双线性模型：s(xi , q) = xiT Wq ；W 为可学习的网络参数。

step3-信息加权平均

step3-信息加权平均：注意力分布 α**i 可以解释为在上下文查询 q 时，第 i 个信息受关注的程度，采用一种“软性”的信息选择机制对输入信息 X** 进行编码为：

这种编码方式为软性注意力机制（soft Attention），软性注意力机制有两种：普通模式（Key=Value=X）和键值对模式（Key！=Value）。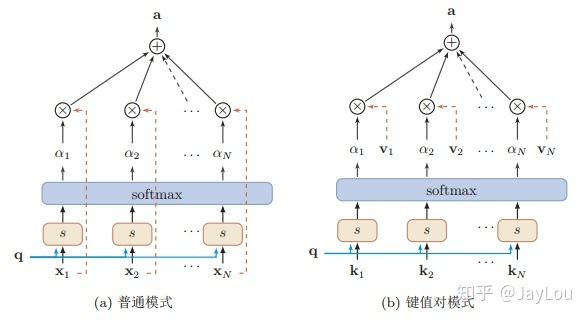

软性注意力机制（soft Attention）

3. Attention机制的变种有哪些？

与普通的Attention机制（上图左）相比，Attention机制有哪些变种呢？

变种1-硬性注意力

变种1-硬性注意力：之前提到的注意力是软性注意力，其选择的信息是所有输入信息在注意力 分布下的期望。还有一种注意力是只关注到某一个位置上的信息，叫做硬性注意力（hard attention）。
硬性注意力有两种实现方式：（1）一种是选取最高概率的输入信息；（2）另一种硬性注意力可以通过在注意力分布式上随机采样的方式实现。
硬性注意力模型的缺点：

硬性注意力的一个缺点是基于最大采样或随机采样的方式来选择信息。因此最终的损失函数与注意力分布之间的函数关系不可导，因此无法使用在反向传播算法进行训练。为了使用反向传播算法，一般使用软性注意力来代替硬性注意力。硬性注意力需要通过强化学习来进行训练。——《神经网络与深度学习》

变种2-键值对注意力

变种2-键值对注意力：即上图右边的键值对模式，此时 Key！=Value 。
比如我们使用键值对 key-value pair 的格式来表示输入信息，其中键用来计算注意力分布 α**i ，值用来计算聚合信息，比如 Self Attention。
用 (K , V) = [( k1 , v1 ) , ⋯ , ( kN , vN )] 来表示 N 组输入信息，给定任务相关的查询向量 q** 时，注意力函数变为：

显然，但 K = V 时，键值对就等价于普通的注意力机制。

变种3-多头注意力

变种3-多头注意力：多头注意力（multi-head attention）是利用多个查询 Q = [ q**1 , q2 , ⋯ , qM** ] ，来平行地计算从输入信息中选取多个信息。每个注意力关注输入信息的不同部分，然后再进行拼接：

4. 自注意力模型（self-Attention model）

一种强大的Attention机制：为什么自注意力模型（self-Attention model）在长距离序列中如此强大？

（1）卷积或循环神经网络难道不能处理长距离序列吗？

当使用神经网络来处理一个变长的向量序列时，我们通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列，如图所示：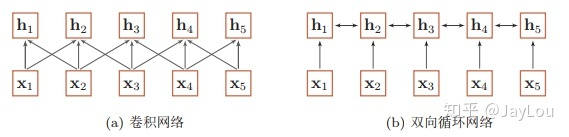

基于卷积网络和循环网络的变长序列编码

从上图可以看出，无论卷积还是循环神经网络其实都是对变长序列的一种“局部编码”：卷积神经网络显然是基于N-gram的局部编码；而对于循环神经网络，由于梯度消失等问题也只能建立短距离依赖。

（2）要解决这种短距离依赖的“局部编码”问题，从而对输入序列建立长距离依赖关系，有哪些办法呢？

如果要建立输入序列之间的长距离依赖关系，可以使用以下两种方法：一 种方法是增加网络的层数，通过一个深层网络来获取远距离的信息交互，另一种方法是使用全连接网络。 ——《神经网络与深度学习》

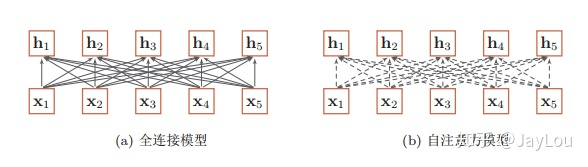
全连接模型和自注意力模型：实线表示为可学习的权重，虚线表示动态生成的权重。

由上图可以看出，全连接网络虽然是一种非常直接的建模远距离依赖的模型， 但是无法处理变长的输入序列。不同的输入长度，其连接权重的大小也是不同的。
这时我们就可以利用注意力机制来“动态”地生成不同连接的权重，这就是自注意力模型（self-attention model）。由于自注意力模型的权重是动态生成的，因此可以处理变长的信息序列。
总体来说，为什么自注意力模型（self-Attention model）如此强大：利用注意力机制来“动态”地生成不同连接的权重，从而处理变长的信息序列。

（3）自注意力模型（self-Attention model）具体的计算流程是怎样的呢?

同样，给出信息输入：用 X = [x**1 , x2 , … , xN**] 表示 N 个输入信息；通过线性变换得到为查询向量序列，键向量序列和值向量序列：

上面的公式可以看出，self-Attention中的Q是对自身（self）输入的变换，而在传统的Attention中，Q来自于外部。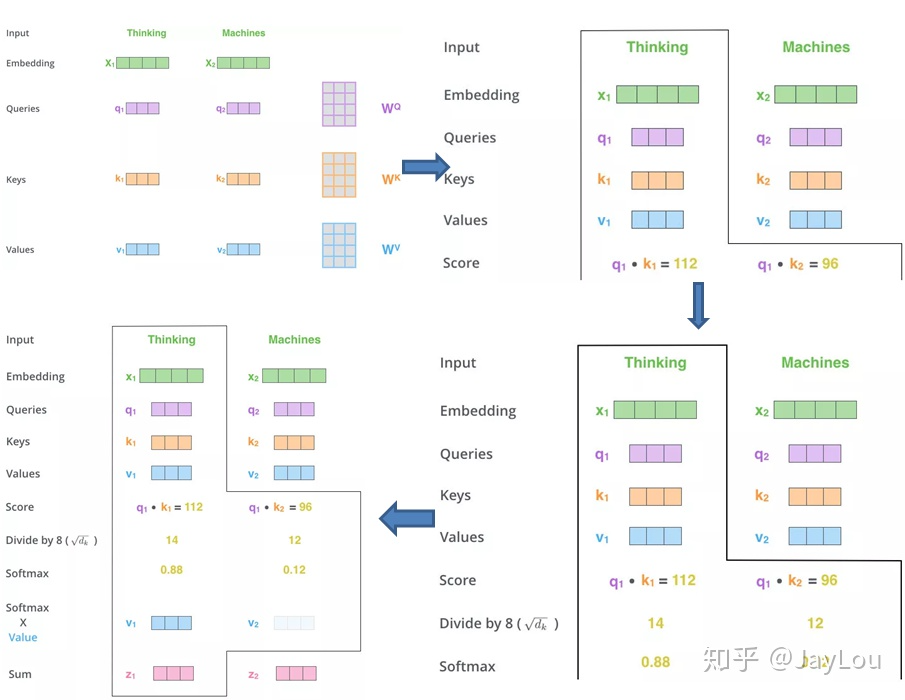

self-Attention计算过程剖解（来自《细讲 | Attention Is All You Need 》）

注意力计算公式为：

自注意力模型（self-Attention model）中，通常使用缩放点积来作为注意力打分函数，输出向量序列可以写为：