参考来源：
CSDN：深入浅出了解GCN原理（公式+代码）
知乎：何时能懂你的心——图卷积神经网络（GCN）
GRAPH CONVOLUTIONAL NETWORKS
知乎：【Graph Neural Network】GCN - 算法原理，实现和应用
B站：图深度表示（GNN）的基础和前沿进展
CSDN：浅谈GCN
百家号：GCN图卷积网络入门详解

GCN 问世已经有几年了（ 2016 年就诞生了），但是这两年尤为火爆。本人愚钝，一直没能搞懂这个 GCN 为何物，最开始是看清华写的一篇三四十页的综述，读了几页就没读了；后来直接拜读 GCN 的开山之作，也是读到中间的数学部分就跪了；再后来在知乎上看大神们的讲解，直接被排山倒海般的公式——什么傅里叶变换、什么拉普拉斯算子等等，给搞蒙了，越读越觉得：“哇这些大佬好厉害，哎我怎么这么菜！”。 就这么反反复复，尝试一次放弃一次，终于慢慢有点理解了，慢慢从那些公式的里跳了出来，看到了全局，也就慢慢明白了 GCN 的原理。今天，我就记录一下我对 GCN “阶段性”的理解。

GCN 的概念首次提出于 ICLR2017（成文于 2016年 ）：
image.png

一、GCN 是做什么的

在扎进 GCN 的汪洋大海前，我们先搞清楚这个玩意儿是做什么的，有什么用。
深度学习一直都是被几大经典模型给统治着，如 CNN、RNN 等等，它们无论再 CV 还是 NLP 领域都取得了优异的效果，那这个 GCN 是怎么跑出来的？是因为我们发现了很多 CNN、RNN 无法解决或者效果不好的问题——图结构的数据。
回忆一下，我们做图像识别，对象是图片，是一个二维的结构，于是人们发明了 CNN 这种神奇的模型来提取图片的特征。CNN 的核心在于它的 kernel，kernel 是一个个小窗口，在图片上平移，通过卷积的方式来提取特征。这里的关键在于图片结构上的平移不变性：一个小窗口无论移动到图片的哪一个位置，其内部的结构都是一模一样的，因此 CNN 可以实现参数共享。这就是 CNN 的精髓所在。
再回忆一下 RNN 系列，它的对象是自然语言这样的序列信息，是一个一维的结构，RNN 就是专门针对这些序列的结构而设计的，通过各种门的操作，使得序列前后的信息互相影响，从而很好地捕捉序列的特征。
上面讲的图片或者语言，都属于欧式空间的数据，因此才有维度的概念，欧式空间的数据的特点就是结构很规则。但是现实生活中，其实有很多很多不规则的数据结构，典型的就是图结构，或称拓扑结构，如社交网络、化学分子结构、知识图谱等等；即使是语言，实际上其内部也是复杂的树形结构，也是一种图结构；而像图片，在做目标识别的时候，我们关注的实际上只是二维图片上的部分关键点，这些点组成的也是一个图的结构。
图的结构一般来说是十分不规则的，可以认为是无限维的一种数据，所以它没有平移不变性。每一个节点的周围结构可能都是独一无二的，这种结构的数据，就让传统的CNN、RNN瞬间失效。所以很多学者从上个世纪就开始研究怎么处理这类数据了。这里涌现出了很多方法，例如 GNN、DeepWalk、node2vec 等等，GCN 只是其中一种，这里只讲 GCN ，其他的后面有空再讨论。
GCN ，图卷积神经网络，实际上跟 CNN 的作用一样，就是一个特征提取器，只不过它的对象是图数据。 GCN 精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding），可见用途广泛。因此现在人们脑洞大开，让 GCN 到各个领域中发光发热。

二、GCN 长啥样，吓人吗

GCN 的公式看起来还是有点吓人的，论文里的公式更是吓破了我的胆儿。但后来才发现，其实 90% 的内容根本不必理会，只是为了从数学上严谨地把事情给讲清楚，但是完全不影响我们的理解，尤其对于我这种“追求直觉，不求甚解”之人。
下面进入正题，我们直接看看 GCN 的核心部分是什么亚子：
假设我们手头有一批图数据，其中有 N 个节点（node），每个节点都有自己的特征，我们设这些节点的特征组成一个 N×D 维的矩阵 X ，然后各个节点之间的关系也会形成一个 N×N 维的矩阵 A ，也称为邻接矩阵（adjacency matrix）。X 和 A 便是我们模型的输入。
GCN 也是一个神经网络层，它的层与层之间的传播方式是：

这个公式中：

  • ， 是单位矩阵
  • 是 的度矩阵(degree matrix)，公式为：
  • 是每一层的特征，对于输入层的话， 就是 （）
  • σ 是非线性激活函数

我们先不用考虑为什么要这样去设计一个公式。我们现在只用知道： 这个部分，是可以事先算好的，因为 由 A 计算而来，而 A 是我们的输入之一。

所以对于不需要去了解数学原理、只想应用 GCN 来解决实际问题的人来说，你只用知道：哦，这个 GCN 设计了一个牛逼的公式，用这个公式就可以很好地提取图的特征。这就够了，毕竟不是什么事情都需要知道内部原理，这是根据需求决定的。
为了直观理解，我们用论文中的一幅图：
image.png
上图中的GCN输入一个图，通过若干层 GCN 每个 node 的特征从 X 变成了 Z ，但是，无论中间有多少层， node 之间的连接关系，即 A ，都是共享的。
假设我们构造一个两层的 GCN ，激活函数分别采用 ReLU 和 Softmax ，则整体的正向传播的公式为：

最后，我们针对所有带标签的节点计算 cross entropy 损失函数：

其中 是具有标签的节点索引集。
就可以训练一个 node classification 的模型了。由于即使只有很少的node有标签也能训练，作者称他们的方法为半监督分类。
当然，你也可以用这个方法去做 graph classification 、link prediction ，只是把损失函数给变化一下即可。

三、GCN 为什么是这个亚子

我前后翻看了很多人的解读，但是读了一圈，最让我清楚明白为什么GCN的公式是这样子的居然是作者Kipf自己的博客：http://tkipf.github.io/graph-convolutional-networks/ 推荐大家一读。

作者给出了一个由简入繁的过程来解释：
我们的每一层 GCN 的输入都是邻接矩阵 A 和 node 的特征 H ，那么我们直接做一个内积，再乘一个参数矩阵 W ，然后激活一下，就相当于一个简单的神经网络层嘛，是不是也可以呢？

实验证明，即使就这么简单的神经网络层，就已经很强大了。这个简单模型应该大家都能理解吧，这就是正常的神经网络操作。
但是这个简单模型有几个局限性：

  • （1）只使用 A 的话，由于 A 的对角线上都是 0 ，所以在和特征矩阵 H 相乘的时候，只会计算一个 node 的所有邻居的特征的加权和，该 node 自己的特征却被忽略了。因此，我们可以做一个小小的改动，给 A 加上一个单位矩阵 I ，这样就让对角线元素变成 1 了。
  • （2）A 是没有经过归一化的矩阵，这样与特征矩阵相乘会改变特征原本的分布，产生一些不可预测的问题。所以我们对 A 做一个标准化处理。首先让 A 的每一行加起来为 1 ，我们可以乘以一个 D-1 ，D 就是度矩阵。我们可以进一步把 D-1 拆开与 A 相乘，得到一个对称且归一化的矩阵： D-1/2AD-1/2 。

通过对上面两个局限的改进，我们便得到了最终的层特征传播公式：

其中 , 为 的 degree matrix（度矩阵） 。
公式中的 与对称归一化拉普拉斯矩阵十分类似，而在谱图卷积的核心就是使用对称归一化拉普拉斯矩阵，这也是 GCN 的卷积叫法的来历。原论文中给出了完整的从谱卷积到 GCN 的一步步推导，我是看不下去的，大家有兴趣可以自行阅读。

从数学角度简单模拟

下面用一个例子记录 GCN 强大公式是如何起作用的。

从图 G 中，我们有一个邻接矩阵 A 和一个度矩阵 D 。同时我们也有特征矩阵 X 。
GCN/图卷积神经网络 - 图3
那么我们怎样才能从邻居节点处得到每一个节点的特征值呢？解决方法就在于 A 和 X 的相乘。
看看邻接矩阵的第一行，我们看到节点 A 与节点 E 之间有连接，得到的矩阵第一行就是与 A 相连接的 E 节点的特征向量（如下图）。同理，得到的矩阵的第二行是 D 和 E 的特征向量之和，通过这个方法，我们可以得到所有邻居节点的向量之和。

GCN/图卷积神经网络 - 图4

此时的计算还存在上述章节提到的局限（1）忽略了节点本身的特征。按理得到的矩阵第一行应该包含结点 A 和 E 的信息，所以做出改进：我们可以通过在A中增加一个单位矩阵I来解决，得到一个新的邻接矩阵。

取 λ=1（使得节点本身的特征和邻居一样重要），我们就有 ，注意，我们可以把 λ 当做一个可训练的参数，但现在只要把 λ 赋值为 1 就可以了，即使在论文中， λ 也只是简单的赋值为 1 。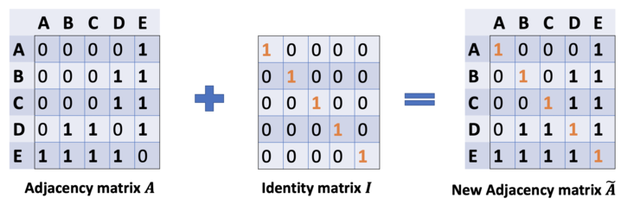
GCN/图卷积神经网络 - 图5
通过给每个节点增加一个自循环，我们得到新的邻接矩阵。

对于局限（2）矩阵缩放，实现归一化。
在矩阵缩放中，通常考虑乘上一个对角矩阵，正好度矩阵 D 为对角矩阵，一定存在这某种关联，所以有了如下的改进：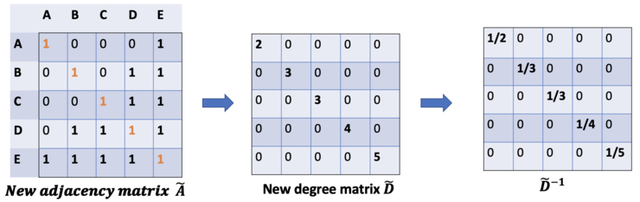
GCN/图卷积神经网络 - 图6
因此，通过 D 取反和 X 的乘法，我们可以取所有邻居节点的特征向量（包括自身节点）的平均值。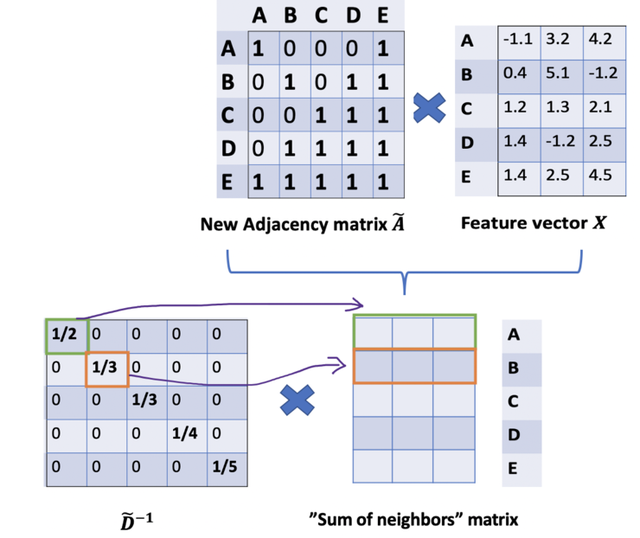
GCN/图卷积神经网络 - 图7
到目前为止一切都很好。但是你可能会问加权平均怎么样？直觉上，如果我们对高低度的节点区别对待，应该会更好。
GCN/图卷积神经网络 - 图8
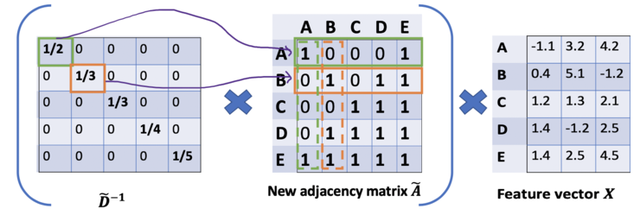
GCN/图卷积神经网络 - 图9
按照上图左乘一个 逆矩阵，我们只是按行缩放(即，行归一化)，而忽略了对应的列（虚线框）。
为列增加一个新的缩放器。
GCN/图卷积神经网络 - 图10
缩放方法给我们提供了 “加权 “的平均值。我们在这里做的是给低度的节点加更多的权重，以减少高度节点的影响。这个加权平均的想法是，我们假设低度节点会对邻居节点产生更大的影响，而高度节点则会产生较低的影响，因为它们的影响力分散在太多的邻居节点上。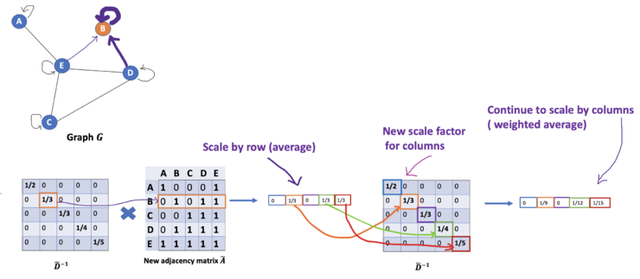
GCN/图卷积神经网络 - 图11
在节点 B 处聚合邻接节点特征时，我们为节点 B 本身分配最大的权重（度数为 3 ），为节点 E 分配最小的权重（度数为 5 ）。
因为我们归一化了两次，所以将”-1 “改为”-1/2”
所以，进行了两次归一化处理，左乘和右乘了 。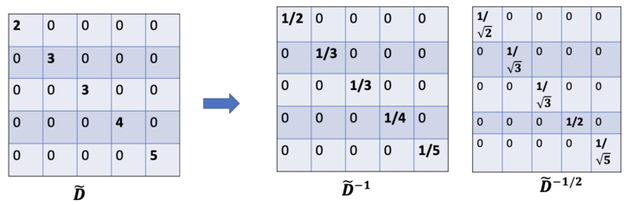
GCN/图卷积神经网络 - 图12

GCN 的实现

GCN 卷积层实现

  1. output = tf.matmul(tf.sparse_tensor_dense_matmul(A, features), self.kernel)
  2.  if self.bias:
  3.      output += self.bias
  4.  act = self.activation(output)

上述代码片段对应的就是 ，只不过多了一个偏置项。

GCN 的实现

  1. def GCN(adj_dim, num_class, feature_dim, dropout_rate=0.5, l2_reg=0, feature_less=True, ):
  2.     Adjs = [Input(shape=(None,), sparse=True)]
  3.     if feature_less:
  4.         X_in = Input(shape=(1,), )
  5.         emb = Embedding(adj_dim, feature_dim, embeddings_initializer=Identity(1.0), trainable=False)
  6.         X_emb = emb(X_in)
  7.         H = Reshape([X_emb.shape[-1]])(X_emb)
  8.     else:
  9.         X_in = Input(shape=(feature_dim,), )
  10.         H = X_in
  12.     H = GraphConvolution(16, activation='relu', dropout_rate=dropout_rate, l2_reg=l2_reg)(
  13.         [H] + Adjs)
  14.     Y = GraphConvolution(num_class, activation='softmax', dropout_rate=dropout_rate, l2_reg=0)(
  15.         [H] + Adjs)
  17.     model = Model(inputs=[X_in] + Adjs, outputs=Y)
  19.     return model

这里 feature_less 的作用是告诉模型我们是否有额外的顶点特征输入，当 feature_less 为 True 的时候，我们直接输入一个单位矩阵作为特征矩阵，相当于对每个顶点进行了 onehot 表示。

GCN 应用

本例中的训练，评测和可视化的完整代码在下面的 git 仓库中，后面还会陆续更新一些其他 GNN 算法
https://github.com/shenweichen/GraphNeuralNetwork
我们使用论文引用网络数据集 Cora 进行测试，Cora 数据集包含 2708 个顶点, 5429 条边,每个顶点包含 1433 个特征，共有 7 个类别。
按照论文的设置，从每个类别中选取 20 个共 140 个顶点作为训练，500 个顶点作为验证集合，1000 个顶点作为测试集。DeepWalk 从全体顶点集合中进行采样，最后使用同样的 140 个顶点训练一个 LR 模型进行分类。

  1. 顶点分类任务结果：

image.png
从分类任务结果可以看到，在使用较少训练样本的条件下 GCN 的效果是高于 DeepWalk 的，而不含顶点特征的 GCN 的效果则会变差很多。
不含顶点特征的 GCN 相当于仅仅在学习图的拓扑结构，而对于图的拓扑结构的学习 GraphEmbedding 方法也能做到，这也说明了 GCN 的优势在于能够同时融入了图的拓扑结构和顶点的特征进行学习。

  1. 顶点向量可视化

DeepWalk 可视化：
image.png
GCN 可视化：
image.png

GCN demo

下面我们实现一个基于 karate_club 网络 GCN demo
image.png

  1. from networkx import karate_club_graph,to_numpy_matrix
  2. import numpy as np
  3. # step1: Data preparation
  4. zkc=karate_club_graph()
  5. order=sorted(list(zkc.nodes()))
  7. NODE_SIZE=len(order)
  8. #Adjacency matrix
  9. A=to_numpy_matrix(zkc,nodelist=order)
  11. #identity matrix
  12. I=np.eye(zkc.number_of_nodes())
  14. node_label = []
  15. for i in range(34):
  16.         label = zkc.node[i]
  17.         if label['club'] == 'Officer':
  18.                 node_label.append(1)
  19.         else:
  20.                 node_label.append(0)
  22. # step2:  Parameter Settings             
  23. NODE_SIZE = 34
  24. NODE_FEATURE_DIM = 34
  25. HIDDEN_DIM1 = 10
  26. num_classes = 2
  27. training_epochs = 100
  28. step = 10
  29. lr=0.1
  31. # step3: network define
  32. X = tf.placeholder(tf.float32, shape=[NODE_SIZE, NODE_FEATURE_DIM])
  33. Y = tf.placeholder(tf.int32, shape=[NODE_SIZE])
  34. label = tf.one_hot(Y, num_classes)
  35. Y_enc = tf.one_hot(Y, 2)
  37. adj = tf.placeholder(tf.float32, shape=[NODE_SIZE, NODE_SIZE])
  38. weights = {"hidden1": tf.Variable(tf.random_normal(dtype=tf.float32, shape=[NODE_FEATURE_DIM, HIDDEN_DIM1]), name='w1'),
  39.            "hidden2": tf.Variable(tf.random_normal(dtype=tf.float32, shape=[HIDDEN_DIM1, num_classes]), 'w1')}
  40. D_hat = tf.matrix_inverse(tf.matrix_diag(tf.reduce_sum(adj, axis=0)))
  41. # GCN layer1
  42. l1 = tf.matmul(tf.matmul(tf.matmul(D_hat, adj), X), weights['hidden1'])
  43. # GCN layer2
  44. output = tf.matmul(tf.matmul(tf.matmul(D_hat, adj), l1), weights['hidden2'])
  46. # step4:define loss func and train
  47. loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=Y_enc, logits=output))
  48. train_op = tf.train.AdamOptimizer(learning_rate=lr).minimize(loss)
  49. init_op = tf.global_variables_initializer()
  50. feed_dict = {adj: A, X: I, Y: node_label}
  51. with tf.Session() as sess:
  52.         sess.run(init_op)
  53.         # dynamic display
  54.         plt.ion()
  55.         for epoch in range(training_epochs):
  56.                 c, _ = sess.run([loss, train_op], feed_dict)
  57.                 if epoch % step == 0:
  58.                         print(f'Epoch:{epoch} Loss {c}')
  60.                 represent = sess.run(output, feed_dict)
  61.                 plt.scatter(represent[:, 0], represent[:, 1], s=200, c=g.node_label)
  62.                 plt.pause(0.1)
  63.                 plt.cla()

模型效果如下：
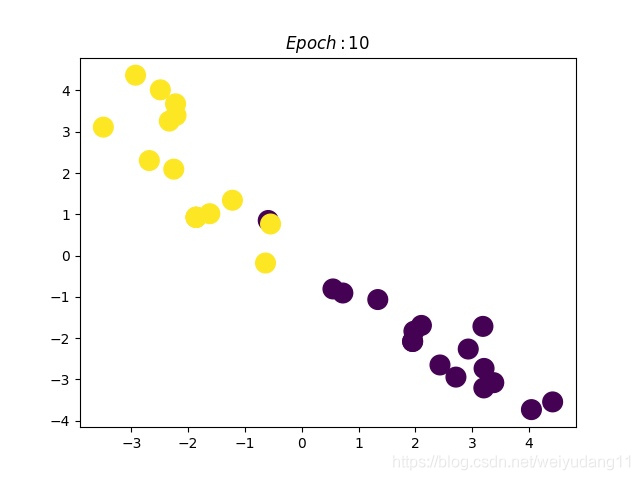
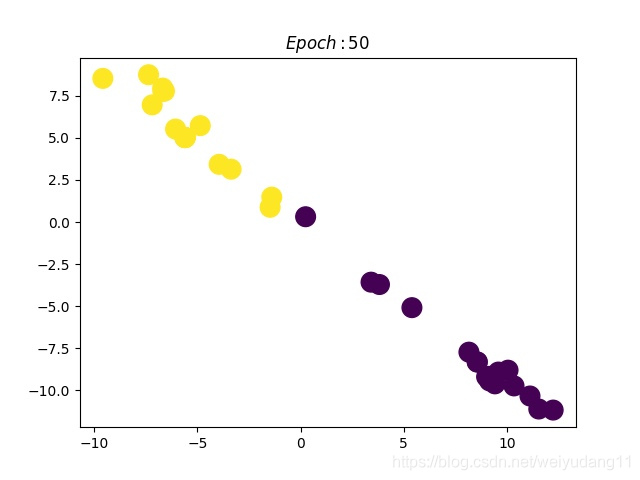
image.png
image.png
image.png
image.png

GCN 能够充分的整合节点的信息，借鉴 PinSage ，可以将 item_id 进行嵌入 embedding ，根据邻居节点的信息实现的嵌入会更加的准确和强大，能够发现文章、视频、图片之间的潜在语义关系，而不仅仅只是内容上的相似。

四、GCN 有多牛

在看了上面的公式以及训练方法之后，我并没有觉得 GCN 有多么特别，无非就是一个设计巧妙的公式嘛，也许我不用这么复杂的公式，多加一点训练数据或者把模型做深，也可能达到媲美的效果呢。
但是一直到我读到了论文的附录部分，我才顿时发现：GCN 原来这么牛啊！
为啥呢？
因为即使不训练，完全使用随机初始化的参数 W ，GCN 提取出来的特征就以及十分优秀了！这跟 CNN 不训练是完全不一样的，后者不训练是根本得不到什么有效特征的。

然后作者做了一个实验，使用一个俱乐部会员的关系网络，使用随机初始化的 GCN 进行特征提取，得到各个 node 的 embedding ，然后可视化：
image.png
可以发现，在原数据中同类别的 node ，经过 GCN 的提取出的 embedding ，已经在空间上自动聚类了。
而这种聚类结果，可以和 DeepWalk 、node2vec 这种经过复杂训练得到的 node embedding 的效果媲美了。
说的夸张一点，比赛还没开始，GCN 就已经在终点了。看到这里我不禁猛拍大腿打呼：“NB！”
还没训练就已经效果这么好，那给少量的标注信息，GCN 的效果就会更加出色。
作者接着给每一类的 node ，提供仅仅一个标注样本，然后去训练，得到的可视化效果如下：
https://zhuanlan.zhihu.com/p/71200936
这是整片论文让我印象最深刻的地方。
看到这里，我觉得，以后有机会，确实得详细地吧 GCN 背后的数学琢磨琢磨，其中的玄妙之处究竟为何，其物理本质为何。这个时候，回忆起在知乎上看到的各路大神从各种角度解读 GCN ，例如从热量传播的角度，从一个群体中每个人的工资的角度，生动形象地解释。这一刻，历来痛恨数学的我，我感受到了一丝数学之美，于是凌晨两点的我，打开了天猫，下单了一本正版《数学之美》。哦，数学啊，你真如一朵美丽的玫瑰，每次被你的美所吸引，都要深深受到刺痛，我何时才能懂得你、拥有你？

其他关于GCN的点滴：

  1. 对于很多网络，我们可能没有节点的特征，这个时候可以使用 GCN 吗？答案是可以的，如论文中作者对那个俱乐部网络，采用的方法就是用单位矩阵 I 替换特征矩阵 X 。
  2. 我没有任何的节点类别的标注，或者什么其他的标注信息，可以使用 GCN 吗？当然，就如前面讲的，不训练的 GCN ，也可以用来提取 graph embedding ，而且效果还不错。
  3. GCN 网络的层数多少比较好？论文的作者做过 GCN 网络深度的对比研究，在他们的实验中发现，GCN 层数不宜多，2-3 层的效果就很好了。

这么强大的玩意儿，赶紧去试试吧！