参考来源：
知乎：一文学会 Pytorch 中的 einsum
实例代码：https://github.com/Ldpe2G/CodingForFun/tree/master/einsum_ex

爱因斯坦求和约定

爱因斯坦求和约定（einsum）提供了一套既简洁又优雅的规则，可实现包括但不限于：向量内积、向量外积、矩阵乘法、转置和张量收缩（tensor contraction）等张量操作，熟练运用 einsum 可以很方便的实现复杂的张量操作，而且不容易出错。

三条基本规则

首先看下 einsum 实现矩阵乘法的例子：

  1. a = torch.rand(2,3)
  2. b = torch.rand(3,4)
  3. c = torch.einsum("ik,kj->ij", [a, b])
  4. # 等价操作 torch.mm(a, b)

其中需要重点关注的是 einsum 的第一个参数 "ik,kj->ij"，该字符串（下文以 equation 表示）表示了输入和输出张量的维度。equation 中的箭头左边表示输入张量，以逗号分割每个输入张量，箭头右边则表示输出张量。表示维度的字符只能是 26 个英文字母 ‘a‘ - ‘z‘。
而 einsum 的第二个参数表示实际的输入张量列表，其数量要与 equation 中的输入数量对应。同时对应每个张量的子 equation 的字符个数要与张量的真实维度对应，比如 "ik,kj->ij" 表示输入和输出张量都是两维的。
equation 中的字符也可以理解为索引，就是输出张量的某个位置的值，是怎么从输入张量中得到的，比如上面矩阵乘法的输出 c 的某个点 c[i, j] 的值是通过 a[i, k] 和b[i, k] 沿着 k 这个维度做内积得到的。

接着介绍两个基本概念，自由索引（**Free indices**）和求和索引（**Summation indices**）：

  • 自由索引：出现在箭头右边的索引，比如上面的例子就是 i 和 j；
  • 求和索引：只出现在箭头左边的索引，表示中间计算结果需要这个维度上求和之后才能得到输出，比如上面的例子就是 k；

接着是介绍三条基本规则：

  1. 规则一，equation 箭头左边，在不同输入之间重复出现的索引表示，把输入张量沿着该维度做乘法操作，比如还是以上面矩阵乘法为例， "ik,kj->ij"，k 在输入中重复出现，所以就是把 a 和 b 沿着 k 这个维度作相乘操作；
  2. 规则二，只出现在 **equation** 箭头左边的索引，表示中间计算结果需要在这个维度上求和，也就是上面提到的求和索引；
  3. 规则三，equation 箭头右边的索引顺序可以是任意的，比如上面的 "ik,kj->ij" 如果写成 "ik,kj->ji"，那么就是返回输出结果的转置，用户只需要定义好索引的顺序，转置操作会在 einsum 内部完成。

特殊规则

特殊规则有两条：

  1. equation 可以不写包括箭头在内的右边部分，那么在这种情况下，输出张量的维度会根据默认规则推导。就是把输入中只出现一次的索引取出来，然后按字母表顺序排列，比如上面的矩阵乘法 "ik,kj->ij" 也可以简化为 "ik,kj"，根据默认规则，输出就是 "ij" 与原来一样；
  2. equation 中支持 "..." 省略号，用于表示用户并不关心的索引，比如只对一个高维张量的最后两维做转置可以这么写：
    1. a = torch.randn(2,3,5,7,9)
    2. # i = 7, j = 9
    3. b = torch.einsum('...ij->...ji', [a])

实际例子解读

接下来将展示 13 个具体的例子，在这些例子中会将 Pytorch einsum 与对应的 Pytorch 张量接口和 python 简单的循环展开实现做对比，希望读者看完这些例子之后能轻松掌握 einsum 的基本用法。
实验代码 github 链接：https://github.com/Ldpe2G/CodingForFun/tree/master/einsum_ex

1. 提取矩阵对角线元素

  1. import torch
  2. import numpy as np
  4. a = torch.arange(9).reshape(3, 3)
  5. # i = 3
  6. torch_ein_out = torch.einsum('ii->i', [a]).numpy()
  7. torch_org_out = torch.diagonal(a, 0).numpy()
  9. np_a = a.numpy()
  10. # 循环展开实现
  11. np_out = np.empty((3,), dtype=np.int32)
  12. # 自由索引外循环
  13. for i in range(0, 3):
  14.     # 求和索引内循环
  15.     # 这个例子并没有求和索引，
  16.     # 所以相当于是1
  17.     sum_result = 0
  18.     for inner in range(0, 1):
  19.         sum_result += np_a[i, i]
  20.     np_out[i] = sum_result
  22. print("input:\n", np_a)
  23. print("torch ein out: \n", torch_ein_out)
  24. print("torch org out: \n", torch_org_out)
  25. print("numpy out: \n", np_out)
  26. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  27. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_ein_out, torch_org_out))
  29. # 终端打印结果
  30. # input:
  31. #  [[0 1 2]
  32. #  [3 4 5]
  33. #  [6 7 8]]
  34. # torch ein out:
  35. #  [0 4 8]
  36. # torch org out:
  37. #  [0 4 8]
  38. # numpy out:
  39. #  [0 4 8]
  40. # is np_out == torch_ein_out ? True
  41. # is torch_org_out == torch_ein_out ? True

2. 矩阵转置

  1. import torch
  2. import numpy as np
  4. a = torch.arange(6).reshape(2, 3)
  5. # i = 2, j = 3
  6. torch_ein_out = torch.einsum('ij->ji', [a]).numpy()
  7. torch_org_out = torch.transpose(a, 0, 1).numpy()
  9. np_a = a.numpy()
  10. # 循环展开实现
  11. np_out = np.empty((3, 2), dtype=np.int32)
  12. # 自由索引外循环
  13. for j in range(0, 3):
  14.     for i in range(0, 2):
  15.         # 求和索引内循环
  16.         # 这个例子并没有求和索引
  17.         # 所以相当于是1
  18.         sum_result = 0
  19.         for inner in range(0, 1):
  20.             sum_result += np_a[i, j]
  21.         np_out[j, i] = sum_result
  23. print("input:\n", np_a)
  24. print("torch ein out: \n", torch_ein_out)
  25. print("torch org out: \n", torch_org_out)
  26. print("numpy out: \n", np_out)
  27. print("is np_out == torch_org_out ?", np.allclose(torch_ein_out, np_out))
  28. print("is torch_ein_out == torch_org_out ?", np.allclose(torch_ein_out, torch_org_out))
  30. # 终端打印结果
  31. # input:
  32. #  [[0 1 2]
  33. #  [3 4 5]]
  34. # torch ein out:
  35. #  [[0 3]
  36. #  [1 4]
  37. #  [2 5]]
  38. # torch org out:
  39. #  [[0 3]
  40. #  [1 4]
  41. #  [2 5]]
  42. # numpy out:
  43. #  [[0 3]
  44. #  [1 4]
  45. #  [2 5]]
  46. # is np_out == torch_org_out ? True
  47. # is torch_ein_out == torch_org_out ? True

3. permute 高维张量转置

  1. import torch
  2. import numpy as np
  4. a = torch.randn(2,3,5,7,9)
  5. # i = 7, j = 9
  6. torch_ein_out = torch.einsum('...ij->...ji', [a]).numpy()
  7. torch_org_out = a.permute(0, 1, 2, 4, 3).numpy()
  9. np_a = a.numpy()
  10. # 循环展开实现
  11. np_out = np.empty((2,3,5,9,7), dtype=np.float32)
  12. # 自由索引外循环
  13. for j in range(0, 9):
  14.     for i in range(0, 7):
  15.         # 求和索引内循环
  16.         # 这个例子没有求和索引
  17.         sum_result = 0
  18.         for inner in range(0, 1):
  19.             sum_result += np_a[..., i, j]
  20.         np_out[..., j, i] = sum_result
  22. print("is np_out == torch_org_out ?", np.allclose(torch_ein_out, np_out))
  23. print("is torch_ein_out == torch_org_out ?", np.allclose(torch_ein_out, torch_org_out))
  25. # 终端打印结果
  26. # is np_out == torch_org_out ? True
  27. # is torch_ein_out == torch_org_out ? True

4. reduce sum

  1. import torch
  2. import numpy as np
  4. a = torch.arange(6).reshape(2, 3)
  5. # i = 2, j = 3
  6. torch_ein_out = torch.einsum('ij->', [a]).numpy()
  7. torch_org_out = torch.sum(a).numpy()
  9. np_a = a.numpy()
  10. # 循环展开实现
  11. np_out = np.empty((1, ), dtype=np.int32)
  12. # 自由索引外循环
  13. # 这个例子中没有自由索引
  14. # 相当于所有维度都加一起
  15. for o in range(0 ,1):
  16.     # 求和索引内循环
  17.     # 这个例子中，i 和 j
  18.     # 都是求和索引
  19.     sum_result = 0
  20.     for i in range(0, 2):
  21.         for j in range(0, 3):
  22.             sum_result += np_a[i, j]
  23.     np_out[o] = sum_result
  25. print("input:\n", np_a)
  26. print("torch ein out: \n", torch_ein_out)
  27. print("torch org out: \n", torch_org_out)
  28. print("numpy out: \n", np_out)
  29. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  30. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_ein_out, torch_org_out))
  32. # 终端打印结果
  33. # input:
  34. #  [[0 1 2]
  35. #  [3 4 5]]
  36. # torch ein out:
  37. #  15
  38. # torch org out:
  39. #  15
  40. # numpy out:
  41. #  [15]
  42. # is np_out == torch_ein_out ? True
  43. # is torch_org_out == torch_ein_out ? True

5. 矩阵按列求和

  1. import torch
  2. import numpy as np
  4. a = torch.arange(6).reshape(2, 3)
  5. # i = 2, j = 3
  6. torch_ein_out = torch.einsum('ij->j', [a]).numpy()
  7. torch_org_out = torch.sum(a, dim=0).numpy()
  9. np_a = a.numpy()
  10. # 循环展开实现
  11. np_out = np.empty((3, ), dtype=np.int32)
  12. # 自由索引外循环
  13. # 这个例子中是 j
  14. for j in range(0, 3):
  15.     # 求和索引内循环
  16.     # 这个例子中是 i
  17.     sum_result = 0
  18.     for i in range(0, 2):
  19.         sum_result += np_a[i, j]
  20.     np_out[j] = sum_result
  22. print("input:\n", np_a)
  23. print("torch ein out: \n", torch_ein_out)
  24. print("torch org out: \n", torch_org_out)
  25. print("numpy out: \n", np_out)
  26. print("is np_out == torch_ein_out ?", np.allclose(torch_org_out, np_out))
  27. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_org_out, torch_ein_out))
  29. # 终端打印输出
  30. # input:
  31. #  [[0 1 2]
  32. #  [3 4 5]]
  33. # torch ein out:
  34. #  [3 5 7]
  35. # torch org out:
  36. #  [3 5 7]
  37. # numpy out:
  38. #  [3 5 7]
  39. # is np_out == torch_ein_out ? True
  40. # is torch_org_out == torch_ein_out ? True

6. 矩阵向量乘法

  1. import torch
  2. import numpy as np
  4. a = torch.arange(6).reshape(2, 3)
  5. b = torch.arange(3)
  6. # i = 2, k = 3
  7. torch_ein_out = torch.einsum('ik,k->i', [a, b]).numpy()
  8. # 等价形式，可以省略箭头和输出
  9. torch_ein_out2 = torch.einsum('ik,k', [a, b]).numpy()
  10. torch_org_out = torch.mv(a, b).numpy()
  12. np_a = a.numpy()
  13. np_b = b.numpy()
  14. # 循环展开实现
  15. np_out = np.empty((2, ), dtype=np.int32)
  16. # 自由索引外循环
  17. # 这个例子是 i
  18. for i in range(0, 2):
  19.     # 求和索引内循环
  20.     # 这个例子中是 k
  21.     sum_result = 0
  22.     for k in range(0, 3):
  23.         sum_result += np_a[i, k] * np_b[k]
  24.     np_out[i] = sum_result
  26. print("matrix a:\n", np_a)
  27. print("vector b:\n", np_b)
  28. print("torch ein out: \n", torch_ein_out)
  29. print("torch ein out2: \n", torch_ein_out2)
  30. print("torch org out: \n", torch_org_out)
  31. print("numpy out: \n", np_out)
  32. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  33. print("is torch_ein_out2 == torch_ein_out ?", np.allclose(torch_ein_out2, torch_ein_out))
  34. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_org_out, torch_ein_out))
  36. # 终端打印输出
  37. # matrix a:
  38. #  [[0 1 2]
  39. #  [3 4 5]]
  40. # vector b:
  41. #  [0 1 2]
  42. # torch ein out:
  43. #  [ 5 14]
  44. # torch ein out2:
  45. #  [ 5 14]
  46. # torch org out:
  47. #  [ 5 14]
  48. # numpy out:
  49. #  [ 5 14]
  50. # is np_out == torch_ein_out ? True
  51. # is torch_ein_out2 == torch_ein_out ? True
  52. # is torch_org_out == torch_ein_out ? True

7. 矩阵乘法

  1. import torch
  2. import numpy as np
  4. a = torch.arange(6).reshape(2, 3)
  5. b = torch.arange(15).reshape(3, 5)
  6. # i = 2, k = 3, j = 5
  7. torch_ein_out = torch.einsum('ik,kj->ij', [a, b]).numpy()
  8. # 等价形式，可以省略箭头和输出
  9. torch_ein_out2 = torch.einsum('ik,kj', [a, b]).numpy() 
  10. torch_org_out = torch.mm(a, b).numpy()
  12. np_a = a.numpy()
  13. np_b = b.numpy()
  14. # 循环展开实现
  15. np_out = np.empty((2, 5), dtype=np.int32)
  16. # 自由索引外循环
  17. # 这个例子是 i 和 j
  18. for i in range(0, 2):
  19.     for j in range(0, 5):
  20.         # 求和索引内循环
  21.         # 这个例子是 k
  22.         sum_result = 0
  23.         for k in range(0, 3):
  24.             sum_result += np_a[i, k] * np_b[k, j]
  25.         np_out[i, j] = sum_result
  27. print("matrix a:\n", np_a)
  28. print("matrix b:\n", np_b)
  29. print("torch ein out: \n", torch_ein_out)
  30. print("torch ein out2: \n", torch_ein_out2)
  31. print("torch org out: \n", torch_org_out)
  32. print("numpy out: \n", np_out)
  33. print("is numpy == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  34. print("is torch_ein_out2 == torch_ein_out ?", np.allclose(torch_ein_out2, torch_ein_out))
  35. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_org_out, torch_ein_out))
  37. # 终端打印输出
  38. # matrix a:
  39. #  [[0 1 2]
  40. #  [3 4 5]]
  41. # matrix b:
  42. #  [[ 0  1  2  3  4]
  43. #  [ 5  6  7  8  9]
  44. #  [10 11 12 13 14]]
  45. # torch ein out:
  46. #  [[ 25  28  31  34  37]
  47. #  [ 70  82  94 106 118]]
  48. # torch ein out2:
  49. #  [[ 25  28  31  34  37]
  50. #  [ 70  82  94 106 118]]
  51. # torch org out:
  52. #  [[ 25  28  31  34  37]
  53. #  [ 70  82  94 106 118]]
  54. # numpy out:
  55. #  [[ 25  28  31  34  37]
  56. #  [ 70  82  94 106 118]]
  57. # is numpy == torch_ein_out ? True
  58. # is torch_ein_out2 == torch_ein_out ? True
  59. # is torch_org_out == torch_ein_out ? True

8. 向量内积

  1. import torch
  2. import numpy as np
  4. a = torch.arange(3)
  5. b = torch.arange(3, 6) # [3, 4, 5]
  6. # i = 3
  7. torch_ein_out = torch.einsum('i,i->', [a, b]).numpy()
  8. # 等价形式，可以省略箭头和输出
  9. torch_ein_out2 = torch.einsum('i,i', [a, b]).numpy()
  10. torch_org_out = torch.dot(a, b).numpy()
  12. np_a = a.numpy()
  13. np_b = b.numpy() 
  14. # 循环展开实现
  15. np_out = np.empty((1, ), dtype=np.int32)
  16. # 自由索引外循环
  17. # 这个例子没有自由索引
  18. for o in range(0, 1):
  19.     # 求和索引内循环
  20.     # 这个例子是 i
  21.     sum_result = 0
  22.     for i in range(0, 3):
  23.         sum_result += np_a[i] * np_b[i]
  24.     np_out[o] = sum_result
  26. print("vector a:\n", np_a)
  27. print("vector b:\n", np_b)
  28. print("torch ein out: \n", torch_ein_out)
  29. print("torch ein out2: \n", torch_ein_out2)
  30. print("torch org out: \n", torch_org_out)
  31. print("numpy out: \n", np_out)
  32. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  33. print("is torch_ein_out2 == torch_ein_out ?", np.allclose(torch_ein_out2, torch_ein_out))
  34. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_org_out, torch_ein_out))
  36. # 终端打印输出
  37. # vector a:
  38. #  [0 1 2]
  39. # vector b:
  40. #  [3 4 5]
  41. # torch ein out:
  42. #  14
  43. # torch ein out2:
  44. #  14
  45. # torch org out:
  46. #  14
  47. # numpy out:
  48. #  [14]
  49. # is np_out == torch_ein_out ? True
  50. # is torch_ein_out2 == torch_ein_out ? True
  51. # is torch_org_out == torch_ein_out ? True

9. 矩阵元素对应相乘并求 reduce sum

  1. import torch
  2. import numpy as np
  4. a = torch.arange(6).reshape(2, 3)
  5. b = torch.arange(6,12).reshape(2, 3)
  6. # i = 2, j = 3
  7. torch_ein_out = torch.einsum('ij,ij->', [a, b]).numpy()
  8. # 等价形式，可以省略箭头和输出
  9. torch_ein_out2 = torch.einsum('ij,ij', [a, b]).numpy()
  10. torch_org_out = (a * b).sum().numpy()
  12. np_a = a.numpy()
  13. np_b = b.numpy() 
  14. # 循环展开实现
  15. np_out = np.empty((1, ), dtype=np.int32)
  16. # 自由索引外循环
  17. # 这个例子没有自由索引
  18. for o in range(0, 1):
  19.     # 求和索引内循环
  20.     # 这个例子是 i 和 j
  21.     sum_result = 0
  22.     for i in range(0, 2):
  23.         for j in range(0, 3):
  24.             sum_result += np_a[i,j] * np_b[i,j]
  25.     np_out[o] = sum_result
  27. print("matrix a:\n", np_a)
  28. print("matrix b:\n", np_b)
  29. print("torch ein out: \n", torch_ein_out)
  30. print("torch ein out2: \n", torch_ein_out2)
  31. print("torch org out: \n", torch_org_out)
  32. print("numpy out: \n", np_out)
  33. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  34. print("is torch_ein_out2 == torch_ein_out ?", np.allclose(torch_ein_out2, torch_ein_out))
  35. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_org_out, torch_ein_out))
  37. # 终端打印输出
  38. # matrix a:
  39. #  [[0 1 2]
  40. #  [3 4 5]]
  41. # matrix b:
  42. #  [[ 6  7  8]
  43. #  [ 9 10 11]]
  44. # torch ein out:
  45. #  145
  46. # torch ein out2:
  47. #  145
  48. # torch org out:
  49. #  145
  50. # numpy out:
  51. #  [145]
  52. # is np_out == torch_ein_out ? True
  53. # is torch_ein_out2 == torch_ein_out ? True
  54. # is torch_org_out == torch_ein_out ? True

10. 向量外积

  1. import torch
  2. import numpy as np
  4. a = torch.arange(3)
  5. b = torch.arange(3,7)  # [3, 4, 5, 6]
  6. # i = 3, j = 4
  7. torch_ein_out = torch.einsum('i,j->ij', [a, b]).numpy()
  8. # 等价形式，可以省略箭头和输出
  9. torch_ein_out2 = torch.einsum('i,j', [a, b]).numpy()
  10. torch_org_out = torch.outer(a, b).numpy()
  12. np_a = a.numpy()
  13. np_b = b.numpy() 
  14. # 循环展开实现
  15. np_out = np.empty((3, 4), dtype=np.int32)
  16. # 自由索引外循环
  17. # 这个例子是 i 和 j
  18. for i in range(0, 3):
  19.     for j in range(0, 4):
  20.         # 求和索引内循环
  21.         # 这个例子没有求和索引
  22.         sum_result = 0
  23.         for inner in range(0, 1):
  24.             sum_result += np_a[i] * np_b[j]
  25.         np_out[i, j] = sum_result
  27. print("vector a:\n", np_a)
  28. print("vector b:\n", np_b)
  29. print("torch ein out: \n", torch_ein_out)
  30. print("torch ein out2: \n", torch_ein_out2)
  31. print("torch org out: \n", torch_org_out)
  32. print("numpy out: \n", np_out)
  33. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  34. print("is torch_ein_out2 == torch_ein_out ?", np.allclose(torch_ein_out2, torch_ein_out))
  35. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_org_out, torch_ein_out))
  37. # 终端打印输出
  38. # vector a:
  39. #  [0 1 2]
  40. # vector b:
  41. #  [3 4 5 6]
  42. # torch ein out:
  43. #  [[ 0  0  0  0]
  44. #  [ 3  4  5  6]
  45. #  [ 6  8 10 12]]
  46. # torch ein out2:
  47. #  [[ 0  0  0  0]
  48. #  [ 3  4  5  6]
  49. #  [ 6  8 10 12]]
  50. # torch org out:
  51. #  [[ 0  0  0  0]
  52. #  [ 3  4  5  6]
  53. #  [ 6  8 10 12]]
  54. # numpy out:
  55. #  [[ 0  0  0  0]
  56. #  [ 3  4  5  6]
  57. #  [ 6  8 10 12]]
  58. # is np_out == torch_ein_out ? True
  59. # is torch_ein_out2 == torch_ein_out ? True
  60. # is torch_org_out == torch_ein_out ? True

11. batch 矩阵乘法

  1. import torch
  2. import numpy as np
  4. a = torch.randn(2,3,5)
  5. b = torch.randn(2,5,4)
  6. # i = 2, j = 3, k = 5, l = 4
  7. torch_ein_out = torch.einsum('ijk,ikl->ijl', [a, b]).numpy()
  8. torch_org_out = torch.bmm(a, b).numpy() 
  10. np_a = a.numpy()
  11. np_b = b.numpy()
  12. # 循环展开实现
  13. np_out = np.empty((2, 3, 4), dtype=np.float32)
  14. # 自由索引外循环
  15. # 这个例子是 i,j和l
  16. for i in range(0, 2):
  17.     for j in range(0, 3):
  18.         for l in range(0, 4):
  19.             # 求和索引内循环
  20.             # 这个例子是 k
  21.             sum_result = 0
  22.             for k in range(0, 5):
  23.                 sum_result += np_a[i, j, k] * np_b[i, k, l]
  24.             np_out[i, j, l] = sum_result
  26. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  27. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_ein_out, torch_org_out))
  29. # 终端打印输出
  30. # is np_out == torch_ein_out ? True
  31. # is torch_org_out == torch_ein_out ? True

12. 张量收缩（tensor contraction）

  1. import torch
  2. import numpy as np
  4. a = torch.randn(2,3,5,7)
  5. b = torch.randn(11,13,3,17,5)
  6. # p = 2, q = 3, r = 5, s = 7
  7. # t = 11, u = 13, v = 17, r = 5
  8. torch_ein_out = torch.einsum('pqrs,tuqvr->pstuv', [a, b]).numpy()
  9. torch_org_out = torch.tensordot(a, b, dims=([1, 2], [2, 4])).numpy()
  11. np_a = a.numpy()
  12. np_b = b.numpy()
  13. # 循环展开实现
  14. np_out = np.empty((2, 7, 11, 13, 17), dtype=np.float32)
  15. # 自由索引外循环
  16. # 这里就是 p,s,t,u和v
  17. for p in range(0, 2):
  18.     for s in range(0, 7):
  19.         for t in range(0, 11):
  20.             for u in range(0, 13):
  21.                 for v in range(0, 17):
  22.                     # 求和索引内循环
  23.                     # 这里是 q和r
  24.                     sum_result = 0
  25.                     for q in range(0, 3):
  26.                         for r in range(0, 5):
  27.                             sum_result += np_a[p, q, r, s] * np_b[t, u, q, v, r]
  28.                     np_out[p, s, t, u, v] = sum_result
  30. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out, atol=1e-6))
  31. print("is torch_ein_out == torch_org_out ?", np.allclose(torch_ein_out, torch_org_out, atol=1e-6))
  33. # 终端打印输出
  34. # is np_out == torch_ein_out ? True
  35. # is torch_ein_out == torch_org_out ? True

13. 二次变换（bilinear transformation）

  1. import torch
  2. import numpy as np
  4. a = torch.randn(2,3)
  5. b = torch.randn(5,3,7)
  6. c = torch.randn(2,7)
  7. # i = 2, k = 3, j = 5, l = 7
  8. torch_ein_out = torch.einsum('ik,jkl,il->ij', [a, b, c]).numpy()
  9. m = torch.nn.Bilinear(3, 7, 5, bias=False)
  10. m.weight.data = b
  11. torch_org_out = m(a, c).detach().numpy()
  13. np_a = a.numpy()
  14. np_b = b.numpy()
  15. np_c = c.numpy()
  16. # 循环展开实现
  17. np_out = np.empty((2, 5), dtype=np.float32)
  18. # 自由索引外循环
  19. # 这里是 i 和 j
  20. for i in range(0, 2):
  21.     for j in range(0, 5):
  22.         # 求和索引内循环
  23.         # 这里是 k 和 l
  24.         sum_result = 0
  25.         for k in range(0, 3):
  26.             for l in range(0, 7):
  27.                 sum_result += np_a[i, k] * np_b[j, k, l] * np_c[i, l]
  28.         np_out[i, j] = sum_result
  30. # print("matrix a:\n", np_a)
  31. # print("matrix b:\n", np_b)
  32. print("torch ein out: \n", torch_ein_out)
  33. print("torch org out: \n", torch_org_out)
  34. print("numpy out: \n", np_out)
  35. print("is np_out == torch_ein_out ?", np.allclose(torch_ein_out, np_out))
  36. print("is torch_org_out == torch_ein_out ?", np.allclose(torch_ein_out, torch_org_out))
  38. # 终端打印输出
  39. # torch ein out:
  40. #  [[-2.9185116   0.17024004 -0.43915534  1.5860008  10.016678  ]
  41. #  [-0.48688257 -3.5114982  -0.7543343  -0.46790922  1.4816089 ]]
  42. # torch org out:
  43. #  [[-2.9185116   0.17024004 -0.43915534  1.5860008  10.016678  ]
  44. #  [-0.48688257 -3.5114982  -0.7543343  -0.46790922  1.4816089 ]]
  45. # numpy out:
  46. #  [[-2.9185114   0.17023998 -0.4391551   1.5860008  10.016678  ]
  47. #  [-0.4868826  -3.5114982  -0.7543342  -0.4679092   1.4816089 ]]
  48. # is np_out == torch_ein_out ? True
  49. # is torch_org_out == torch_ein_out ? True

从上面的13个例子可以看出，只要确定了自由索引和求和索引，einsum 的输出计算都可以用一套比较通用的多层循来实现，外层的循环对应自由索引，内层循环对应求和索引。

Pytorch einsum 实现简要解读

C++ 代码解读：

github 代码链接：https://github.com/pytorch/pytorch/blob/53596cdb7359116e8c8ae18ffef06f2677ad1296/aten/src/ATen/native/Linear.cpp#L148

我只读懂了大概的实现思路，然后按照我自己的理解添加了注释（仅供参考）：

  1. // 为了方便理解，我简化了大部分代码，
  2. // 并把对于 "..." 省略号的处理去掉了
  3. /** 
  4.  * 代码实现主要分为3大步：
  5.  * 1. 解析 equation，分别得到输入和输出对应的字符串
  6.  * 2. 补全输出和输入张量的维度，通过 permute 操作对齐输入和输出的维度
  7.  * 3. 将维度对齐之后的输入张量相乘，然后根据求和索引累加
  8. */
  9. Tensor einsum(std::string equation, TensorList operands) {
  10.   // ......
  11.   // 把 equation 按照箭头分割
  12.   // 得到箭头左边输入的部分
  13.   const auto arrow_pos = equation.find("->");
  14.   const auto lhs = equation.substr(0, arrow_pos);
  15.   // 获取输入操作数个数
  16.   const auto num_ops = operands.size();
  18.   // 下面循环主要作用是解析 equation 左边输入部分，
  19.   // 按 ',' 号分割得到每个输入张量对应的字符串，
  20.   // 并把并把每个 char 字符转成 int， 范围 [0, 25] 
  21.   // 新建 vector 保存每个输入张量对应的字符数组
  22.   std::vector<std::vector<int>> op_labels(num_ops);
  23.   std::size_t curr_op = 0;
  24.   for (auto i = decltype(lhs.length()){0}; i < lhs.length(); ++i) {
  25.     switch (lhs[i]) {
  26.       // ......
  27.       case ',': 
  28.         // 遇到逗号，接下来解析下一个输入张量的字符串
  29.         ++curr_op;
  30.         // ......
  31.         break;
  32.       default:
  33.         // ......
  34.         // 把 char 字符转成 int 
  35.         op_labels[curr_op].push_back(lhs[i] - 'a');
  36.     }
  37.   }
  39.   // TOTAL_LABELS = 26
  40.   constexpr int TOTAL_LABELS = 'z' - 'a' + 1;
  41.   std::vector<int> label_count(TOTAL_LABELS, 0); 
  42.   // 遍历所有输入操作数
  43.   // 统计 equation 中 'a' - 'z' 每个字符的出现次数
  44.   for(const auto i : c10::irange(num_ops)) {
  45.     const auto labels = op_labels[i];
  46.     for (const auto& label : labels) {
  47.       // ......
  48.       ++label_count[label];
  49.     }
  50.     // ......
  51.   }
  53.   // 创建一个 vector 用于保存 equation 
  54.   // 箭头右边输出的字符到索引的映射
  55.   std::vector<int64_t> label_perm_index(TOTAL_LABELS, -1);
  57.   int64_t perm_index = 0;
  58.   // ......
  59.   // 接下来解析输出字符串
  60.   if (arrow_pos == std::string::npos) {
  61.     // 处理用户省略了箭头的情况，
  62.     // ......
  63.   } else {
  64.     // 一般情况
  65.     // 得到箭头右边的输出
  66.     const auto rhs = equation.substr(arrow_pos + 2);
  67.     // 遍历输出字符串并解析
  68.     for (auto i = decltype(rhs.length()){0}; i < rhs.length(); ++i) {
  69.       switch (rhs[i]) {
  70.         // ......
  71.         default:
  72.           // ......
  73.           const auto label = rhs[i] - 'a';
  74.           // ......
  75.           // 建立字符到索引的映射，perm_index从0开始
  76.           label_perm_index[label] = perm_index++;
  77.       }
  78.     }
  79.   }
  81.   // 保存原始的输出维度大小
  82.   const int64_t out_size = perm_index;
  83.   // 对齐输出张量的维度，使得对齐之后的维度等于
  84.   // 自由索引加上求和索引的个数
  85.   // 对输出补全省略掉的求和索引
  86.   // 也就是在输入等式中出现，但是没有在输出等式中出现的字符
  87.   for (const auto label : c10::irange(TOTAL_LABELS)) {
  88.     if (label_count[label] > 0 && label_perm_index[label] == -1) {
  89.       label_perm_index[label] = perm_index++;
  90.     }
  91.   }
  93.   // 对所有输入张量，同样补齐维度至与输出维度大小相同
  94.   // 最后对输入做 permute 操作，使得输入张量的每一维
  95.   // 与输出张量的每一维能对上
  96.   std::vector<Tensor> permuted_operands;
  97.   for (const auto i: c10::irange(num_ops)) {
  98.     // 保存输入张量最终做 permute 时候的维度映射
  99.     std::vector<int64_t> perm_shape(perm_index, -1);
  100.     Tensor operand = operands[i];
  101.     // 取输入张量对应的 equation
  102.     const auto labels = op_labels[i];
  103.     std::size_t j = 0;
  104.     for (const auto& label : labels) {
  105.       // ......
  106.       // 建立当前遍历到的输入张量字符到
  107.       // 输出张量的字符到的映射
  108.       // label: 当前遍历到的字符
  109.       // label_perm_index: 保存了输出字符对应的索引
  110.       // 所以 perm_shape 就是建立了输入张量的每一维度
  111.       // 与输出张量维度的对应关系
  112.       perm_shape[label_perm_index[label]] = j++;
  113.     }
  114.     // 如果输入张量的维度小于补全后的输出
  115.     // 那么 perm_shape 中一定存在值为 -1 的元素
  116.     // 那么相当于需要扩充输入张量的维度
  117.     // 扩充的维度添加在张量的尾部 
  118.     for (int64_t& index : perm_shape) {
  119.       if (index == -1) {
  120.         // 在张量尾部插入维度1
  121.         operand = operand.unsqueeze(-1);
  122.         // 修改了perm_shape中的index，
  123.         // 因为是引用取值
  124.         index = j++;
  125.       }
  126.     }
  127.     // 把输入张量的维度按照输出张量的维度重排，采用 permute 操作
  128.     permuted_operands.push_back(operand.permute(perm_shape)); 
  129.   }
  130.   // ......
  131.   Tensor result = permuted_operands[0];
  132.   // .....
  133.   // 计算最终结果
  134.   for (const auto i: c10::irange(1, num_ops)) {
  135.     Tensor operand = permuted_operands[i];
  136.     // 新建 vector 用于保存求和索引
  137.     std::vector<int64_t> sum_dims;
  138.     // ......
  139.     // 详细的代码可以阅读 Pytorch 源码
  140.     // 这里我还没有完全理解 sumproduct_pair 的实现，
  141.     // 里面用的是 permute + bmm，
  142.     // 不过我觉得可以简单理解为
  143.     // 将张量做广播乘法，再根据求和索引做累加
  144.     result = sumproduct_pair(result, operand, sum_dims, false);
  145.   }
  146.   return result;
  147. }

图解实现

下面还是用矩阵乘法来说明 C++ 的实现思路，下图展示的是矩阵乘法的通用实现：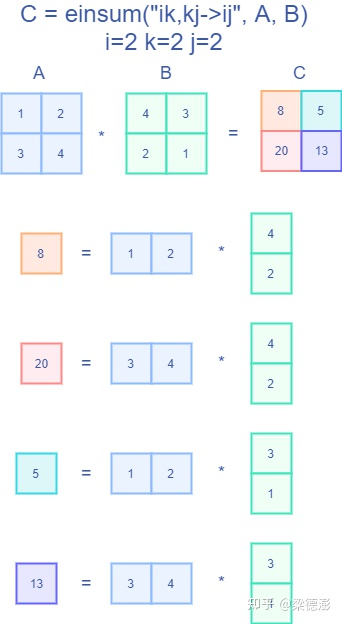
image.png
接下来展示 C++ 的实现思路：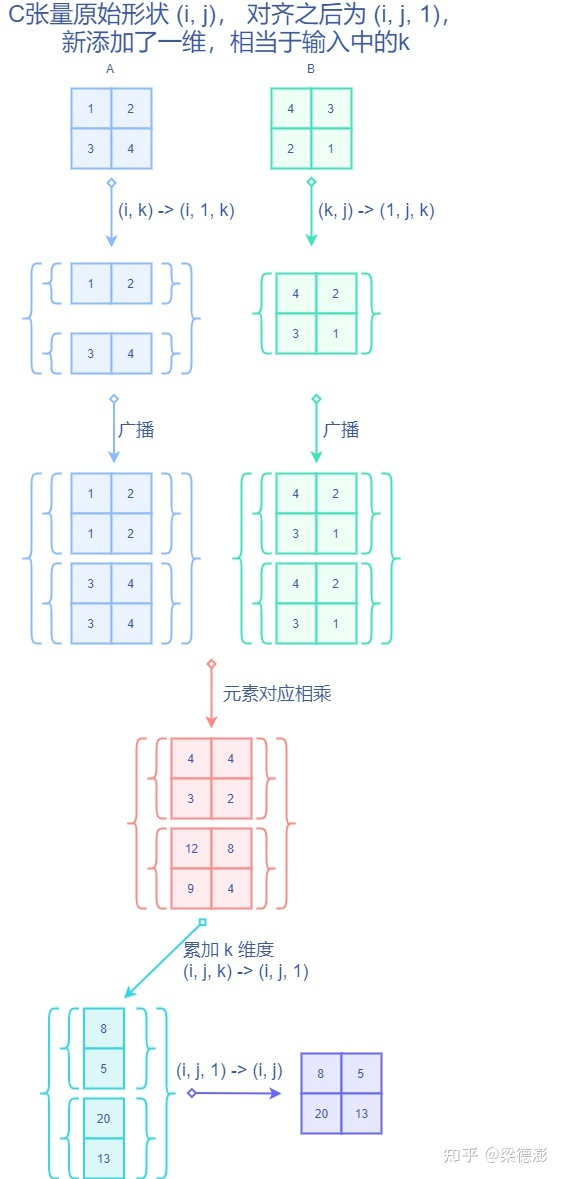
image.png

总结

通过上面的实际例子和代码解读，可以看到 einsum 非常灵活，可以方便的实现各种常用的张量操作。希望读者通过这篇文章也可以轻松掌握 einsum 的基本用法。文中对于 Pytorch C++实现代码的解析是基于我自己的理解，如果觉得有误或者不理解的地方欢迎讨论。

参考资料