1、MNIST数据集

似乎所有程序员在学习一个新的程序语言时，都想要打印输出一个“hello world”，它代表了你入门了这门语言。那么，MNIST手写数字识别便是入门机器学习和深度学习的“hello world”。跑通MNIST程序便能大致了解机器学习的流程，包括数据的读取、转换（totensor）、归一化、神经网络模型设计、超参数设计、训练、前向传播、后向传播等等。在入门机器学习之前先自己跑通一遍MNIST识别程序具有非凡的意义。
MNIST（Mixed National Institute of Standards and Technologydatabase）是一个手写数字的大型数据库，拥有60,000个示例的训练集和10,000个示例的测试集。更详细的介绍可以查看 Yann LeCun的MNIST数据集官网。

2、代码

本程序来自pytorch官方提供的MNIST示例代码，链接：https://github.com/pytorch/examples/blob/master/mnist/main.py
在经过修改并添加训练结果可视化和特征图可视化等功能，github链接在本文最下方

下面讲解train.py中的代码：

2.1 导入模块

  1. from __future__ import print_function # 这个是python当中让print都以python3的形式进行print，即把print视为函数
  2. import argparse
  3. import os
  4. import numpy as np
  6. import torch
  7. import torch.nn as nn
  8. import torch.nn.functional as F
  9. import torch.optim as optim
  10. from torchvision import datasets, transforms
  11. from torch.optim.lr_scheduler import StepLR
  12. from pathlib import Path
  13. import time
  15. # import network
  16. from model.network.LeNet import LeNet
  17. from model.network.MyNetV1 import MyNetV1
  18. from model.network.MyNetV2 import MyNetV2
  19. from model.network.DefaultNet import DefaultNet
  20. from model.network.LeNet5 import LeNet5
  21. from model.network.MyFullConvNet import MyFullConvNet
  22. from model.network.MyVggNet import MyVggNet

导入训练网络需要的模块，其中值得注意的是：

  • argparse模块，该模块允许你在运行.py文件时可以附带参数，如：python train.py —model lenet
  • torch基本模块，即pytorch基本的库
  • matplotlib模块，用于绘制loss曲线和acc曲线图，也用于显示模型中各层特征图即特征图可视化

2.2 函数参数

通过argparse模块，可以在运行文件时添加运行所需要的参数。这些参数可以用于设置网络模型的超参数，如学习率、batch-size、epochs、训练模型等等。下面贴出代码：

  1.     # Training settings
  2.     parser = argparse.ArgumentParser(description="Pytorch MNIST Example")
  3.     parser.add_argument("--batch-size", type=int, default=64, metavar="N",
  4.                         help="input batch size for training (default : 64)")
  5.     parser.add_argument("--test-batch-size", type=int, default=1000, metavar="N",
  6.                         help="input batch size for testing (default : 1000)")
  7.     parser.add_argument("--epochs", type=int, default=64, metavar="N",
  8.                         help="number of epochs to train (default : 64)")
  9.     parser.add_argument("--learning-rate", type=float, default=0.1, metavar="LR",
  10.                         help="number of epochs to train (default : 14)")
  11.     parser.add_argument("--gamma", type=float, default=0.5, metavar="M",
  12.                         help="Learning rate step gamma (default : 0.5)")
  13.     parser.add_argument("--no-cuda", action="store_true", default=True,
  14.                         help="disables CUDA training")
  15.     parser.add_argument("--dry-run", action="store_true", default=False,
  16.                         help="quickly check a single pass")
  17.     parser.add_argument("--seed", type=int, default=1, metavar="S",
  18.                         help="random seed (default : 1)")
  19.     parser.add_argument("--log-interval", type=int, default=10, metavar="N",
  20.                         help="how many batches to wait before logging training status")
  21.     parser.add_argument("--save-model", action = "store_true", default=True,
  22.                         help="For saving the current Model")
  23.     parser.add_argument("--load_state_dict", type=str, default="no",
  24.                         help="load the trained model weights or not (default: no)")
  25.     parser.add_argument("--model", type=str, default="LeNet",
  26.                         help="choose the model to train (default: LeNet)")
  27.     args = parser.parse_args()

值得注意的是：

  • batch-size：批训练大小，单次训练用的样本数。通常以pytorch-MNIST手写数字识别与特征图可视化 - 图1为大小。如果batch-size过小，就好像你每次数钱只数一张（而不是好几张一起数），训练数据效率就低下，且收敛困难；如果batch-size过大，虽然相对处理速度加快，但是所需要的内容容量增加，可能会出现 CPU/GPU 内存容量不足等情况，所以需要根据图片具体大小、模型复杂度和计算机性能之间权衡batch-size的大小
  • epochs：一个epoch表示所有的数据送入网络中完成一次前向传播和后向传播的过程
  • leaning-rate：学习率
  • load_state_dict：继续模型训练/重新开始训练。假设上次的训练效果不理想，你想在上次的基础上继续训练，就可以添加这个选项，训练前加载之前生成的权重文件
  • gamma：调整学习率中所用的参数，调整方法为StepLR

其他参数大概就是字面意思。要注意必须有args = parse.parse_args()这一句，意思是把爬取到的参数信息赋值到变量args上，后续便可以通过args得到参数值，比如args.model， args.learning_rate

2.3 数据加载与transform

以下代码是程序加载数据和对数据进行转化（ToTensor）的代码：

  1.     train_kwargs = {"batch_size": args.batch_size}
  2.     test_kwargs = {"batch_size": args.test_batch_size}
  3.     if use_cuda:
  4.         cuda_kwargs = {"num_workers": 1, "pin_memory": True, "shuffle": True}
  5.         train_kwargs.update(cuda_kwargs)
  6.         test_kwargs.update(cuda_kwargs)
  8.     transform = transforms.Compose([
  9.         transforms.ToTensor(),
  10.         # normalize(mean, std, inplace=False) mean各通道的均值， std各通道的标准差， inplace是否原地操作
  11.         # 这里说的均值是数据里的均值
  12.         # output = (input - mean) / std
  13.         # 归一化到-1 ~ 1，也不一定，但是属于标准化
  14.         transforms.Normalize((0.1307, ), (0.3081, ))
  15.     ])
  16.     dataset1 = datasets.MNIST("./data", train=True, download=True,
  17.                             transform=transform)
  18.     dataset2 = datasets.MNIST("./data", train=False,
  19.                             transform=transform)
  20.     train_loader = torch.utils.data.DataLoader(dataset1, **train_kwargs)
  21.     test_loader = torch.utils.data.DataLoader(dataset2, **test_kwargs)

num_workers是多进程的加载数，pin_memory是是否将数据保存在pin memory区，pin memory中的数据转到CPU会比较快。另外几个值得注意的点是：

  1. 加载数据集
  • train=True即加载训练集，false即加载训练集
  • download即是否下载数据集，如果数据集不存在，则代码会自动下载数据集到指定路径中；若存在，则略过
  • shuffle是打乱
  1. 数据转换与归一化
  • 数据原本是二进制文件，通过transform将其转换成可训练的tensor张量
  • 因为数据集都是一通道的黑白图片，像素值为0-255，为了方便计算，需要将其归一化，这样做可以让收敛更快。其中mean是数据里的均值，std是各通道的标准差

2.4 训练

  1. graph_loss = []
  2. graph_acc = []
  4. def train(args, model, device, train_loader, optimizer, epoch):
  5.     # 这里的train和上面的train不是一个train
  6.     model.train()
  7.     start_time = time.time()
  8.     tmp_time = start_time
  9.     for batch_idx, (data, target) in enumerate(train_loader):
  10.         data, target = data.to(device), target.to(device)
  11.         optimizer.zero_grad()
  12.         output = model(data)
  13.         loss = F.nll_loss(output, target)
  14.         loss.backward()
  15.         optimizer.step()
  16.         if batch_idx % args.log_interval == 0:
  17.             print("Train Epoch: {} [{}/{} ({:.0f}%)]\t Loss: {:.6f}\t Cost time: {:.6f}s".format(
  18.                 epoch, batch_idx * len(data), len(train_loader.dataset),
  19.                 100. * batch_idx / len(train_loader), loss.item(), time.time() - tmp_time
  20.             ))
  21.             tmp_time = time.time()
  22.             graph_loss.append(loss.item())
  23.             if args.dry_run:
  24.                 break
  25.     end_time = time.time()
  26.     print("Epoch {} cost {} s".format(epoch, end_time - start_time))

定义全局变量graph_lossand graph_acc分别记录训练过程中的准确率和损失，最后写入.txt文件中，方便后续查看和数据可视化。简单的说一下训练的流程：

  1. 从dataloader中获取数据集的数据和与之对应的标签，即data，target，并放到device中（CPU/GPU）
  2. 初始化optimizer的梯度为0
  3. 数据送入模型处理
  4. 根据输出和实际标签计算loss值。这里采用的损失函数是nll_loss，也是一种交叉熵损失函数。它和CrossEntropyLoss的区别是，nll_loss没有包含softmax这一步，所以它适合模型结尾带有softmax的网络
  5. 根据损失值进行后向传播
  6. 后向传播的工具是优化器，优化器开始后向传播
  7. 每隔一个log_interval输出当前的训练结果，比如损失值、当前epoch完成百分比和时间

仔细的理解训练过程的每一步，便知道机器学习的原理大概是怎么样的

2.5 测试

测试训练结果在代码在test_model.py里，测试内容是测试集的前1000张图片（这个数字可以在argparse里面修改）。输入

  1. python test_model.py --model lenet

便得到测试结果：
image.png

3、训练结果可视化

在训练的过程中，我将训练的结果存放在graph_loss和graph_acc里，并且在训练结束之后，将两个列表中的数据存储到.txt文件当中。现在，便可以从.txt文件中读取训练结果并显示出来。用于画图的工具是matplotlib，而相关的代码文件是draw_graph.py，以下为代码：

  1. import matplotlib
  2. import os
  3. import numpy as np
  4. from matplotlib import pyplot as plt
  5. import argparse
  6. import sys
  8. parser = argparse.ArgumentParser()
  9. parser.add_argument("--model", type=str, default="lenet")
  10. args = parser.parse_args()
  12. #file_loss_path = "E:/WorkSpace/Pytorch/mnist/model/result/{}_loss.txt".format(args.model)
  13. file_loss_path = sys.path[0] + "/model/result/{}_loss.txt".format(args.model)
  15. lst_loss = list()
  16. with open(file_loss_path) as file_object:
  17.     for line in file_object:
  18.         if "e" in line:
  19.             lst_loss.append(eval(line))
  20.         else:
  21.             lst_loss.append(float(line[:-2]))
  22.     file_object.close()
  24. #file_acc_path = "E:/WorkSpace/Pytorch/mnist/model/result/{}_acc.txt".format(args.model)
  25. file_acc_path = sys.path[0] +  "/model/result/{}_acc.txt".format(args.model)
  26. lst_acc = list()
  27. with open(file_acc_path) as file_object:
  28.     for line in file_object:
  29.         if "e" in line:
  30.             lst_acc.append(eval(line))
  31.         else:
  32.             lst_acc.append(float(line[:-2]))
  33.     file_object.close()
  34. print(lst_acc)
  36. plt.title("{} loss".format(args.model))
  37. plt.plot(lst_loss)
  38. plt.xlim(0 - len(lst_loss) / 20, len(lst_loss))
  39. plt.ylim(0, 1.5)
  40. plt.grid()
  41. plt.savefig(file_loss_path[:-3] + "jpg")
  43. plt.title("{} acc".format(args.model))
  44. plt.plot(lst_acc)
  45. plt.xlim(0 - len(lst_acc) / 20, len(lst_acc))
  46. plt.ylim(min(lst_acc) - 1, max(max(lst_acc) + 1, 100))
  47. plt.savefig(file_acc_path[:-3] + "jpg")

通过matplotlib，读取.txt文件中的数据，将其以图表的形式显示并且保存下来，以下为效果：
64个epcoh的训练准确率：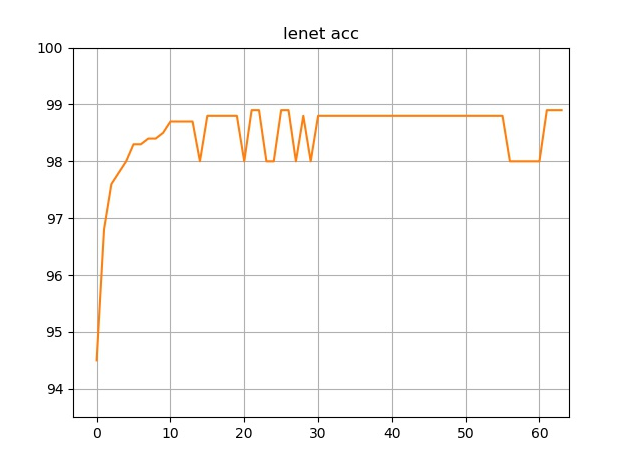
image.png
训练过程中的损失：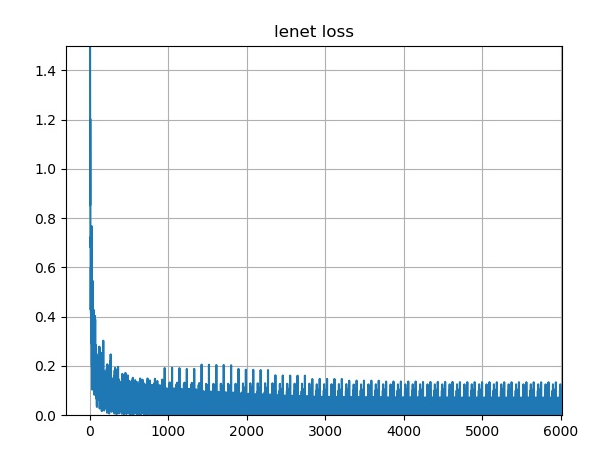
image.png

3.1 多模型准确率汇总

在学习本程序的过程中，我也在学习一些经典网络，比如LeNet, AlexNet, VggNet等，所以尝试着自己搭建网络并将经典网络中的优点融入其中，以下为不同网络准确率：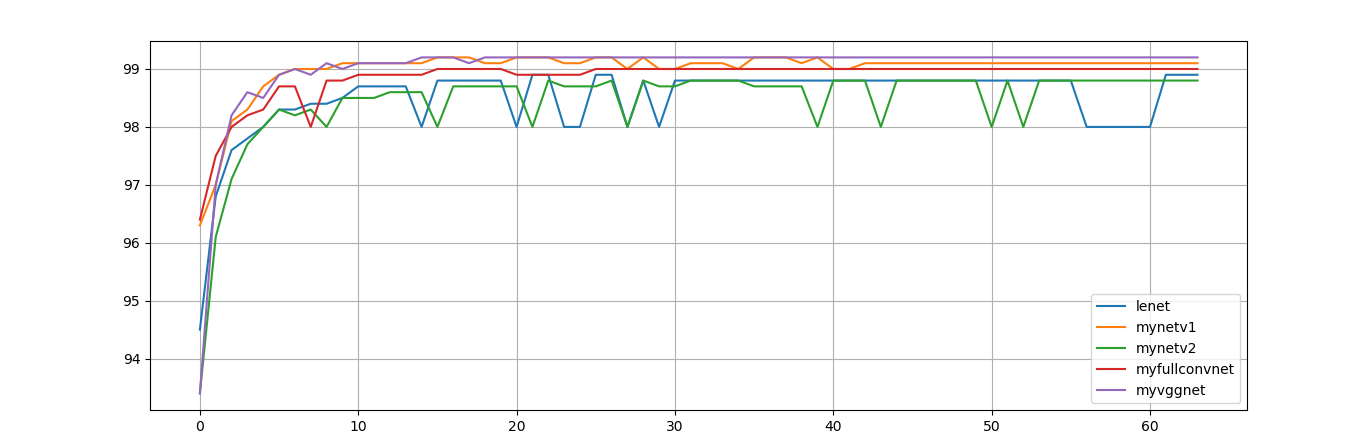
image.png

  • LeNet，最经典的网络，包含了基本的卷积神经网络结构。可见由于其网络结构过于简单，其准确率有较大的抖动，但是有不错的准确率
  • MyFullConvNet，运用了更多的卷积层，并且用卷积层代替第一个全连接层，效果比LeNet要好
  • MyNetV1，这也是我自己设计的网络结构，其中的设计思想是：① 尽可能的使用小卷积核，参数量更少； ② 使用stride = 2的卷积核来代替池化层，这样虽然参数量有所增加，但是弥补了池化层会过滤掉过多信息的缺点； ③ 使用dropout技术，使网络降低过拟合。
  • MyNetV2，本来是想用卷积层代替更多的其他层，于是用了输出通道数比输出通道数小的卷积层，但结果并不理想，甚至比LeNet准确率还要低
  • MyVggNet，参考了VggNet的特性修改的网络，用多个小卷积层的堆叠替代大卷积层，这样做的优势是感受野不变，但是增加了更多非线性的因素（因为每一层卷积后都跟一个relu激活函数）。事实证明，更深的网络的确能带来更好的效果，并且观察训练结果可以发现，更深的网络更加稳定，不易抖动。

4、特征图可视化

光是看代码，是难以理解卷积神经网络是如何识别数字的。所以不如将卷积神经网络中每一层输出的特征图显示出来，便能知道在卷积神经网络这个黑盒子里，到底发生了什么。

实现特征图可视化的基本思想是：卷积神经网络处理的数据类型是tensor（张量），张量是无法用于显示图片的，所以需要将其转换成可以显示为图片的数据类型，比如numpy。再通过matplotlib，将其显示出来。

具体代码请到我的github上查看，在本文的最下方

4.1 原图

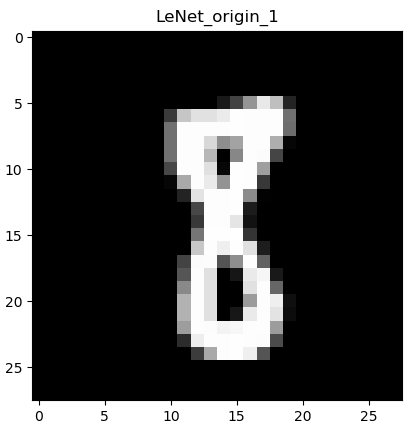
下图是测试集中一个手写数字“8”的图片：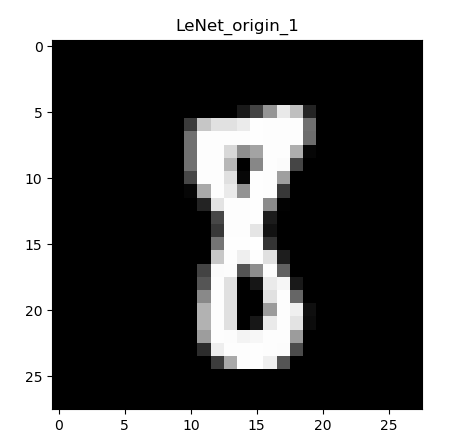
image.png
通过观察图片和观察具体tensor的输出可以发现，MNIST数据集存放的是一通道的黑白图片，其中的像素值是0~255，其特征较为简单。

4.2 卷积后的特征图

下图是经过一次卷积之后的特征图：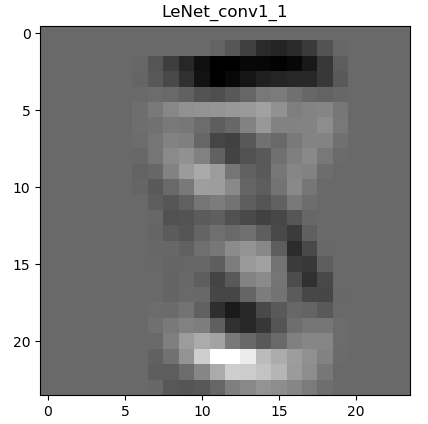
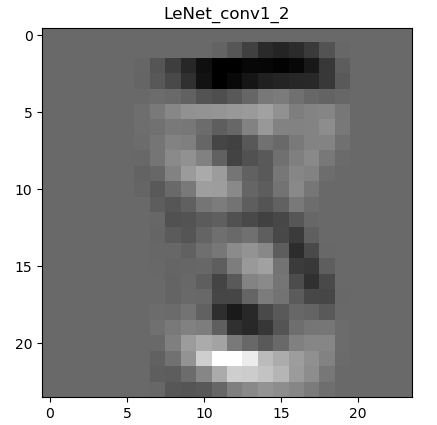
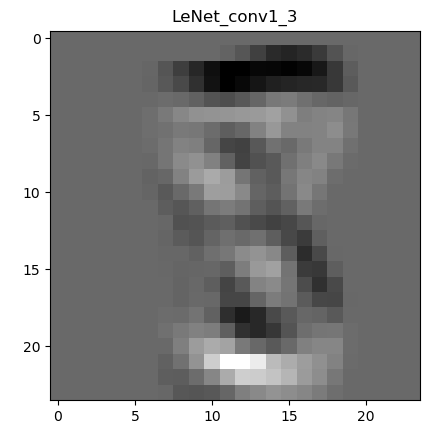
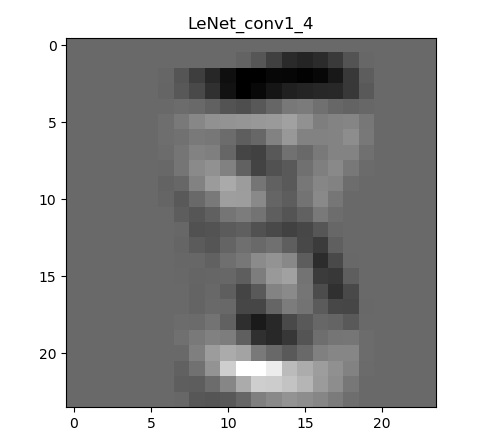
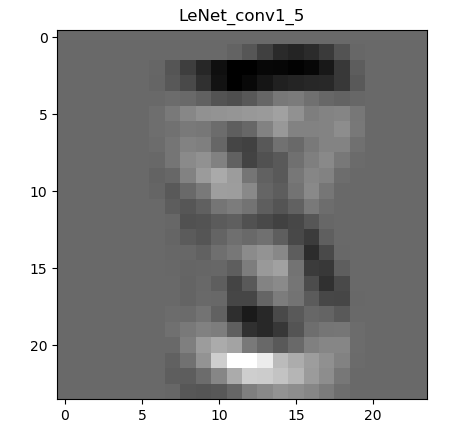
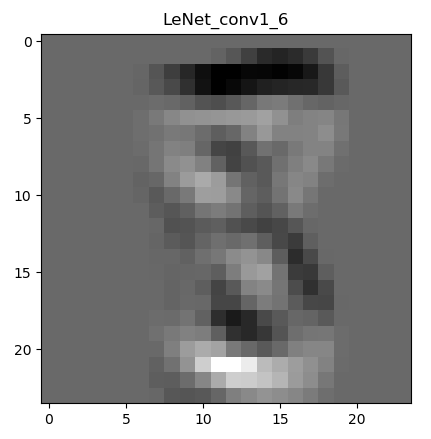
image.pngimage.pngimage.pngimage.pngimage.pngimage.png
为什么会有6张呢，因为第一层的卷积层输出通道数是6，所以会生成6张不同的特征图。虽然看着感觉六个特征图差别不大，那是因为数据集过于简单，如果是复杂一些的图片，便能看到其不同。图片经过卷积之后，图像像素从28 28变成了26 26。现在用肉眼还能勉强看出来是个数字8。

4.3 激活函数relu后的特征图

下面显示卷积->ReLu激活函数后的图像：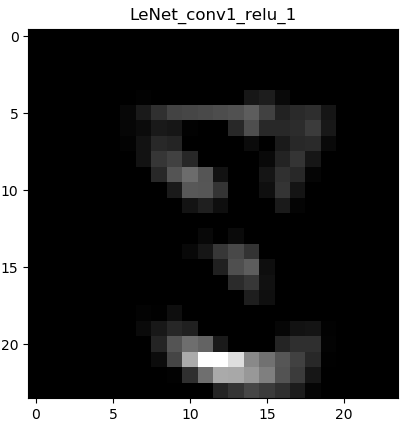
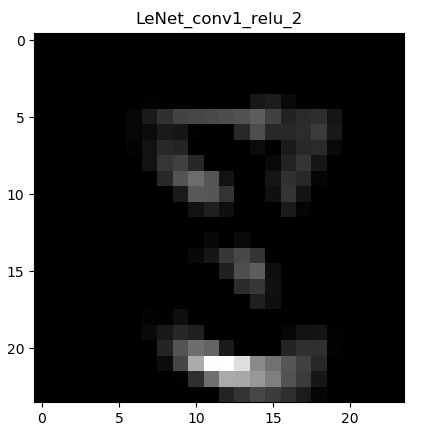
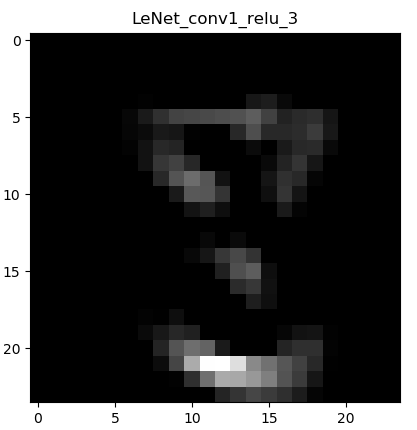
image.pngimage.pngimage.png
这一层的输出同样是6张，但是由于篇幅就不全部贴出来了。看了图像之后马上就能理解，ReLu激活函数干了什么。通俗的讲：将黑的地方变得更黑，白的地方保持不变。ReLu的表达式：
pytorch-MNIST手写数字识别与特征图可视化 - 图16
使小于0的数字等于0，大于0的数字则保持不变。（因为训练过程中，图像数据都是经过归一化处理的，使得像素值的范围为-1~1）。

4.4 最大池化后的特征图

下面显示卷积->ReLu激活函数->最大池化层的图像：
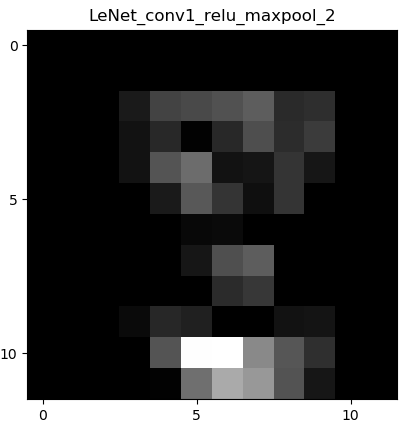
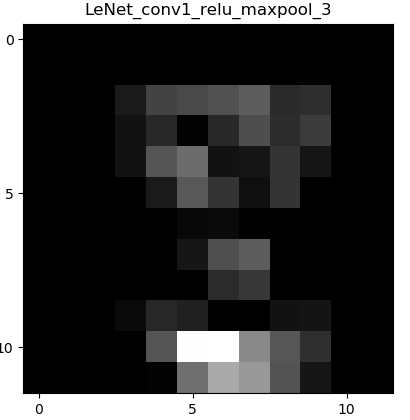
image.pngimage.pngimage.png
显而易见，图像经过最大池化层之后，像素缩小了一半，这也正是池化层（下采样）的作用：缩小图像尺寸。能减少网络的计算量，也能在一定程度上缓解过拟合的问题。但这只是一定程度上，并且池化层可能会过滤掉很多有用的特征。
值得注意的是，本程序用的池化层都是最大池化max_pooling，所以可以发现，相比较前一层的特征图，整体图片的亮度变得更亮了，因为最大池化是选择区域中值最大的值进行保留。

4.4 最后的特征图

下图显示的是多次卷积和激活函数和最大池化后的图片：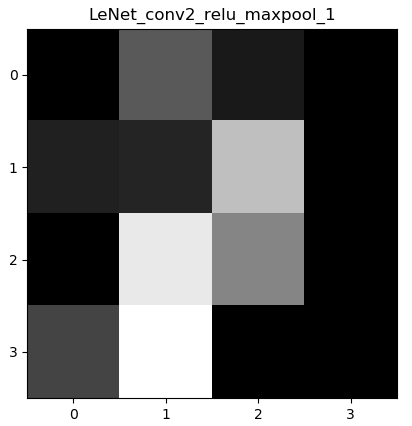
image.png
可以看到，经过多次卷积、激活函数和池化层之后，图像已经“面目全非”，肉眼已经完全分辨不出图片原本代表着什么数字。但是对于神经网络来说，图片永远只是一堆数字，这张图片也是神经网络计算出来的数字特征。在经过这一步之后，通过将图片展平即变为一维向量x = x.view(x.size(0), -1)。由于是最后一层是4 4 16的输出，所以展平后就得到了长度为4 4 16 = 256的一维向量。再通过全连接层，可将一维向量变为长度为10的输出（0-9共10类）。

4.5 输出

因为进入全连接层之后，tensor已经变为了一维向量，无法以图片的形式显示，所以只能输出看具体的数字。以下为LeNet全连接层的代码：

  1. self.fc1 = nn.Linear(16 * 4 * 4, 120)
  2. self.fc2 = nn.Linear(120, 84)
  3. self.fc3 = nn.Linear(84, 10)

并且输出全连接层各个位置的张量大小以及最后一层的输出：

  1. x = x.view(x.size(0), -1)
  2. print(x[0].size())
  3. x = self.fc1(x)
  4. print(x[0].size())
  5. x = F.relu(x)
  6. x = self.fc2(x)
  7. print(x[0].size())
  8. x = F.relu(x)
  9. x = self.fc3(x)
  10. print(x[0])

输出结果如下：
image.png
image.png
可以看到，展平后的张量长度的确为256，经过一层全连接层之后长度变为120，然后是84，最后输出最后一层的张量。可以看到，张量每个元素的值代表着该类的概率，由于该图片识别为8，所以在index为8的地方值最大，最后得出该手写体为数字“8”的结论。softmax也是根据张量计算出最后的预测值。