1. IOU 考虑1个因素 (Intersection Over Union)

IOU是使用最多的目标检测定位评测方法，IOU全程为intersection over union，中文为交并比。其公式为：

用图来表示就是：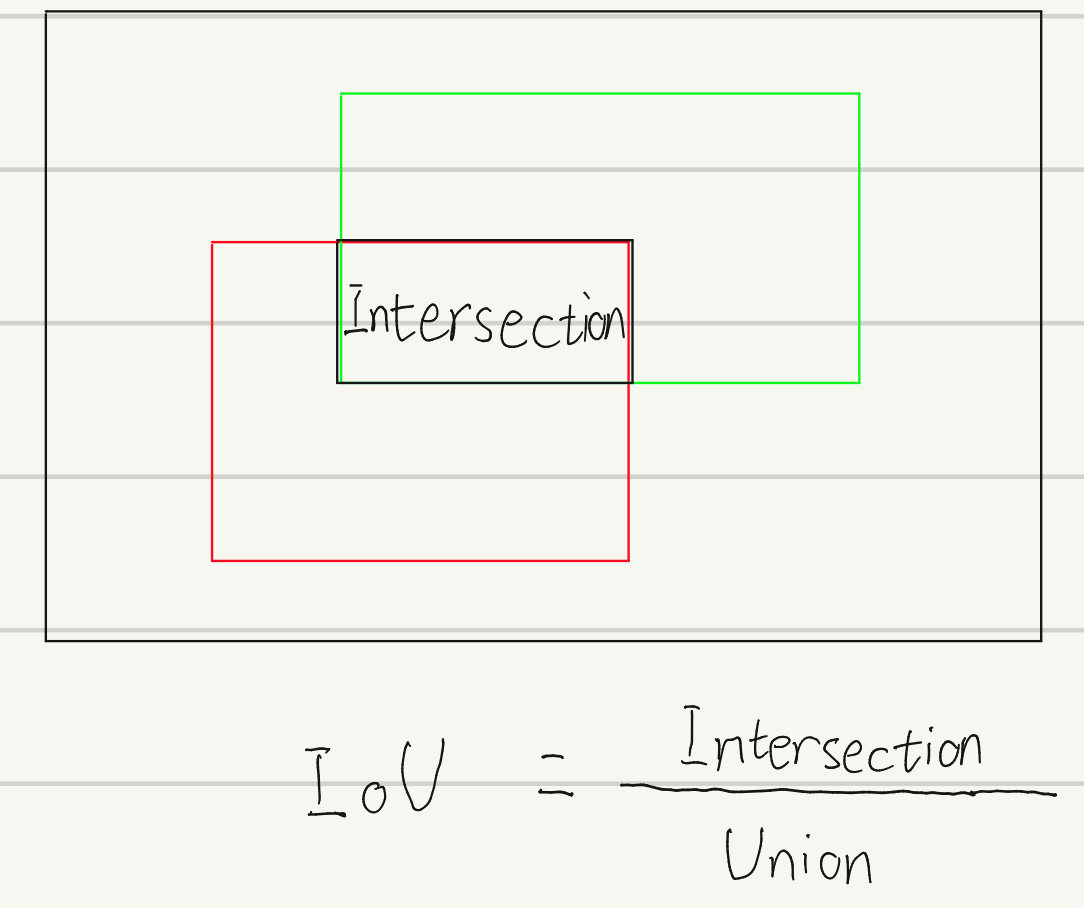

缺点：
使用IOU来作为目标检测的loss函数时，会遇到以这种困境：
预测框和真实框没有交集，导致IOU值为0，网络无法从中学到任何信息。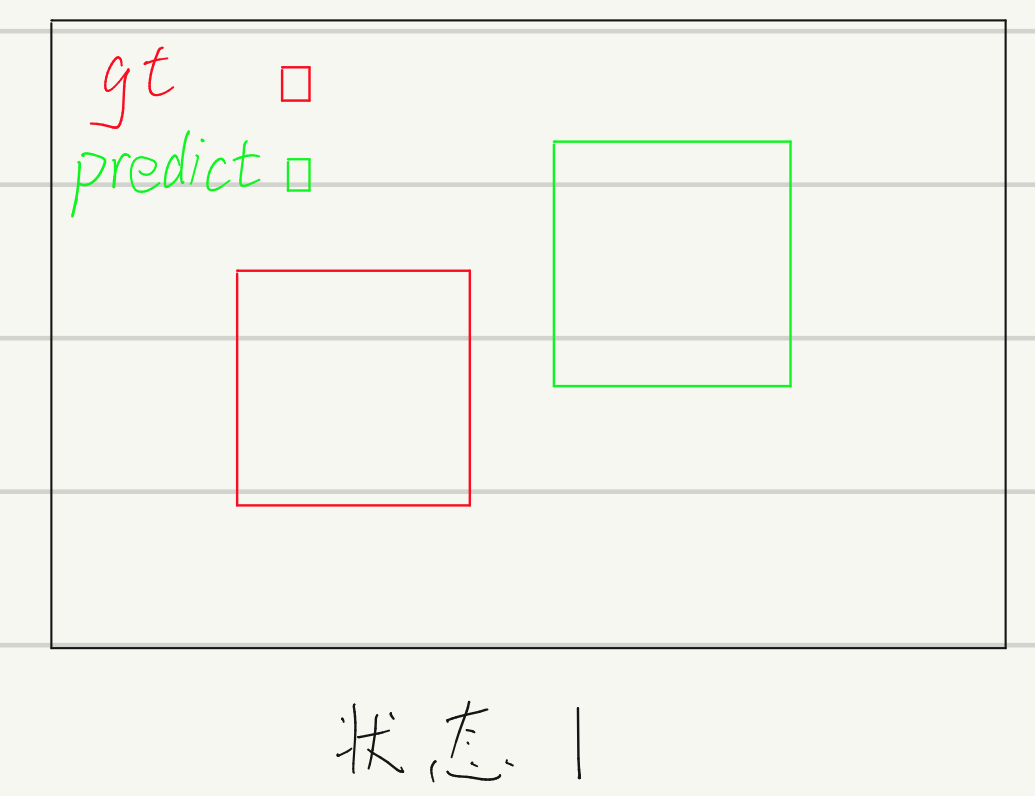

2. GIoU 考虑2个因素 (Generalized IoU)

为了解决IOU真实框和预测框没有交集的困境，学者提出了GIoU（Generalized IoU）。GIoU的公式为：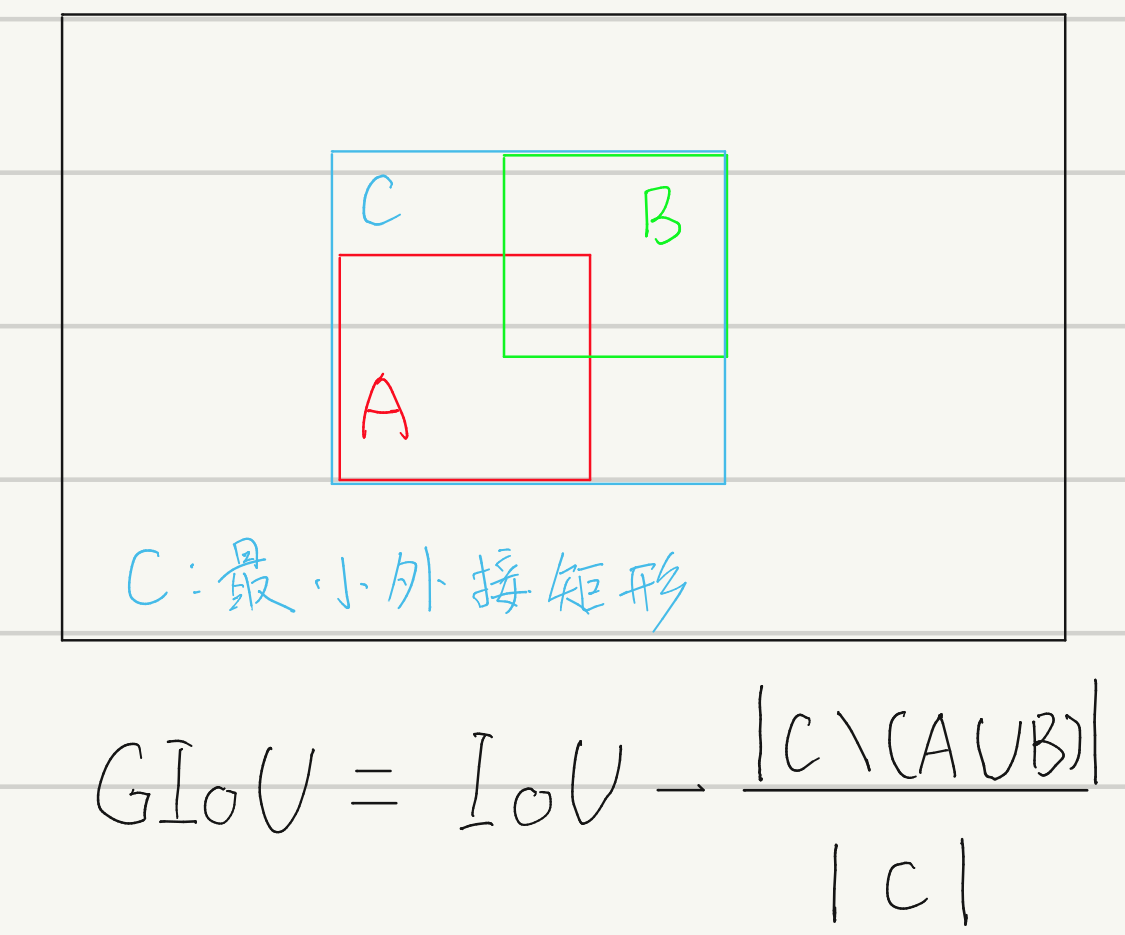



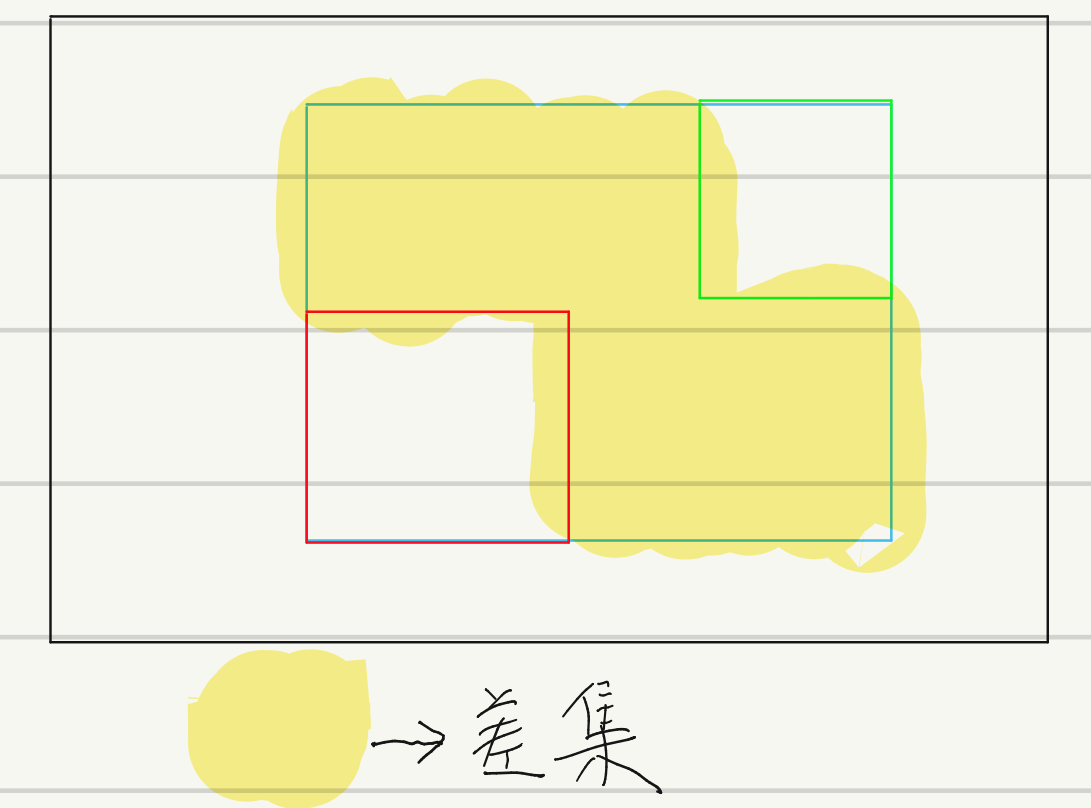
缺点：
GIOU并没有解决IOU的所有问题，还有两种情况：

1. 当多个预测框与真实框的IOU一致时，即使它们在真实框的不同方位，其GIOU值依然不会改变，如图状态2所示；
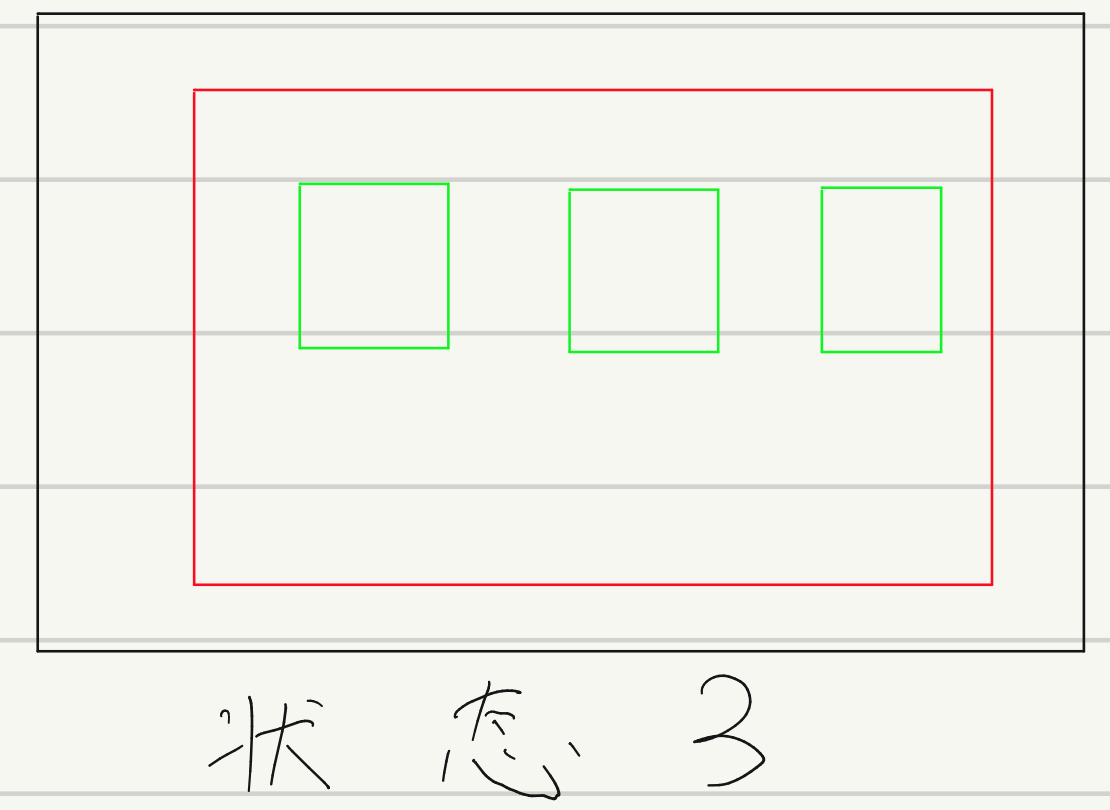
2. 当预测框在真实框的内部时，若预测框长宽不变，它在真实框中的任意位置都不会改变GIOU的值，如图状态3所示；

这明显不是一个目标检测loss想要的结果，如图：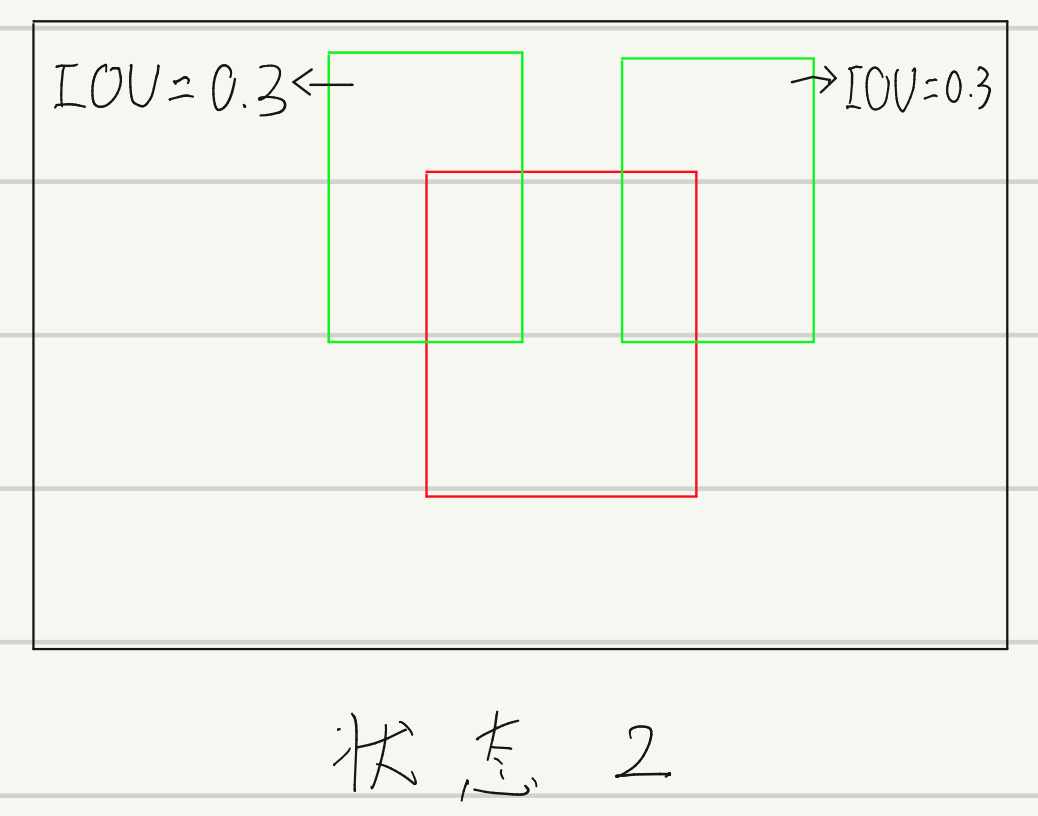


一句话总结：GIoU同时考虑了交并比（IoU）、最小外接矩形（其实和DIoU的距离类似）

3. DIoU 考虑2个因素 (Distance IoU)

DIoU从另一个层面代替了GIoU的功能。
为了解决IOU和GIOU存在的问题，学者提出了DIoU（Distance IoU），作者主要从以下两个方面思考：

1. 如何最小化预测框和真实框之间的归一化距离？
2. 如何在预测框和真实框重叠时，回归的更准确？

针对第一个问题，作者提出了DIoU，公式如下：

其中\rho表示两点的欧几里得距离，b表示框的中心点位置，c表示最小外界矩形的对角线长度。相比于GIOU，DIOU的限制不是直接考虑两个框之间的差集，而是直接限制了最小外界矩形框的面积和两个框中心点的距离，从抽象意义上来说，这使得网络在反向传播的时候更加倾向于移动bbox的位置来减少loss。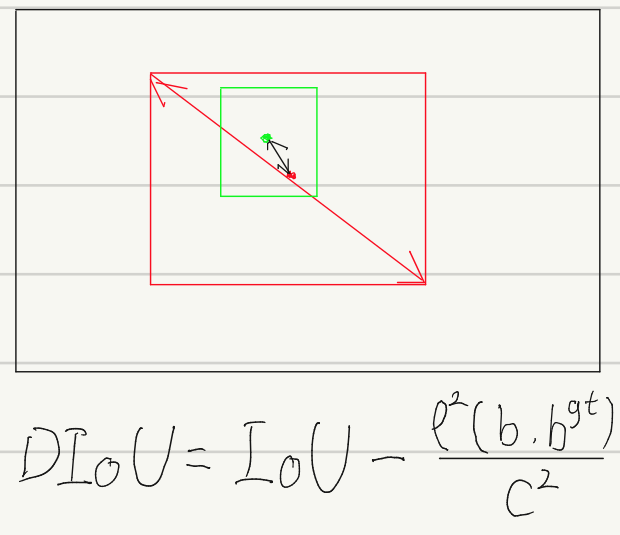

那么第二个问题呢？也就是之前提到的状态2。当两个预测框和真实框的中心点距离一样，最小外界矩形框的对角线长度也一样，DIOU的值是相同的。DIOU并没有解决这个问题。

一句话总结：DIoU同时考虑了交并比（IoU）、距离（中心点距离）

4. CIoU 考虑3个因素 (Complete IoU)

于是学者们继续研究，提出了CIoU，直接给出公式：



a为权重系数。v这一项考虑了长宽比

一句话总结：CIoU同时考虑了预测框和GT框之间的距离（中心点距离）、重叠率（IoU）、长宽比。

5. SIoU 考虑4个因素 (Scaylla IoU)

Scaylla (ˈsɪlə) 斯库拉，是希腊神话中吞吃水手的女海妖。她的身体有六个头十二只脚，并且有猫的尾巴。

SIoU考虑四个因素：

1. Angle cost
2. Distance cost
3. Shape cost
4. IoU cost

   5.1 angle cost

   
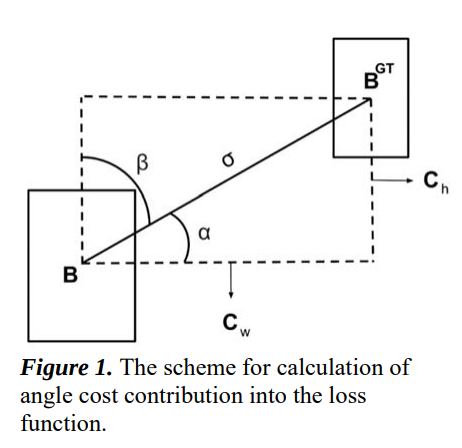
   angle loss的表达式为：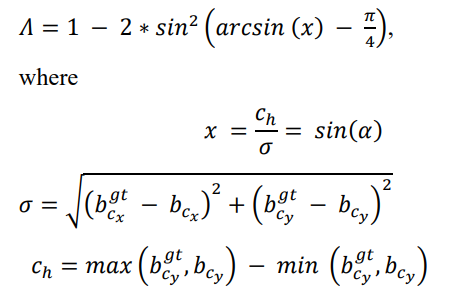
   
   简单理解为：angle loss使得预测框趋向于向本来就靠近的轴（x轴或者y轴）继续靠近。如本来在y轴就很接近了，那他会使得y轴更接近，而先不考虑x轴。
   

   5.2 distance cost

   
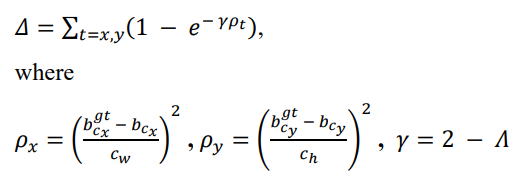
   当a趋向于0°或这90°的时候，distance cost的值大大降低
   没懂

   5.3 shape cost

   𝜃 的值定义了每个数据集的Shape cost及其值是唯一的。𝜃 的值是这个等式中非常重要的一项，它控制着整体的loss对Shape cost的关注程度。如果 𝜃 的值设置为 1，它将立即优化一个Shape，从而损害Shape的自由移动。为了计算 𝜃 的值，作者将遗传算法用于每个数据集，实验上 𝜃 的值接近 4，文中作者为此参数定义的范围是 2 到 6。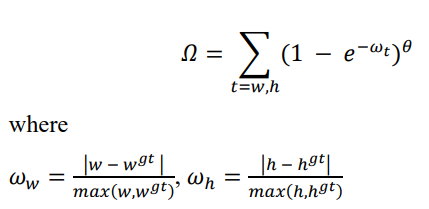
   
   其实就是考虑了真实框和预测框的长宽比，然后用一个次方项Θ来控制量级

   5.4 iou cost

   交并比。