题目描述

原题链接

给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例 1：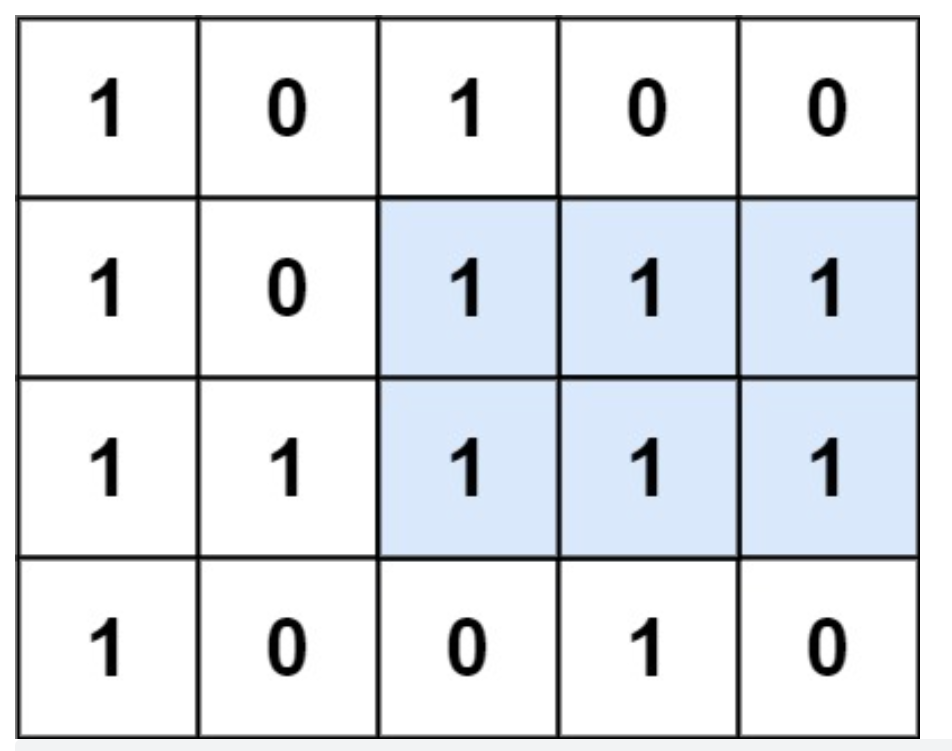

输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = []
输出：0

示例 3：

输入：matrix = [["0"]]
输出：0

示例 4：

输入：matrix = [["1"]]
输出：1

示例 5：

输入：matrix = [["0","0"]]
输出：0

提示：

• rows == matrix.length

cols == matrix[0].length
1 <= row, cols <= 200
matrix[i][j] 为 ‘0’ 或 ‘1’

个人解法

Java

JavaScript

更优解法

Java

暴力解法

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int m=matrix.length,n=matrix[0].length;
        if (m == 0) {
            return 0;
        }
        //用于记录每个点为右下角时，左边最大连续1的数量(包括自己)
        int[][] left=new int[m][n];
        for (int i=0;i<m;i++){
            for (int j=0;j<n;j++){
                if (matrix[i][j]=='1'){
                    left[i][j]=(j==0 ? 0: left[i][j-1])+1;
                }
            }
        }
        int ressult=0;
        for (int i=0;i<m;i++){
            for (int j=0;j<n;j++){
                if (matrix[i][j]=='0'){
                    continue;
                }
                //初始矩形宽度
                int width=left[i][j];
                //初始面积，为右下角时，最小的面积也有这么大
                int area =width;
                for (int k=i-1;k>=0;k--){
                    width=Math.min(width,left[k][j]);
                    area=Math.max(area,(i-k+1)*width);
                }
                ressult=Math.max(ressult,area);
            }
        }
        return ressult;
    }
}

单调栈

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        int[] left = new int[len];
        int[] right = new int[len];
        Stack<Integer> stack = new Stack<>();
        stack.push(-1);
        for (int i = 0; i < len; i++) {
            while (stack.peek() != -1 && heights[i] <= heights[stack.peek()]) {
                stack.pop();
            }
            left[i] = stack.peek();
            stack.push(i);
        }
        stack = new Stack<>();
        stack.push(-1);
        for (int i = len-1; i >=0; i--) {
            while (stack.peek() != -1 && heights[i] <= heights[stack.peek()]) {
                stack.pop();
            }
            if (stack.peek()==-1){
                right[i]=len;
            }else {
                right[i] = stack.peek();
            }
            stack.push(i);
        }
        int max=-1;
        for (int i=0;i<len;i++){
            max=Math.max(max,(right[i]-left[i]-1)*heights[i]);
        }
        return max;
    }
 public int maximalRectangle(char[][] matrix) {
        int m=matrix.length,n=matrix[0].length;
        if (m == 0) {
            return 0;
        }
        int[] height=new int[n];
        int ressult=0;
        for (int i=0;i<m;i++){
            for (int j=0;j<n;j++){
                if (matrix[i][j]=='1'){
                    height[j]+=1;
                }else {
                    height[j]=0;
                }
            }
            ressult=Math.max(ressult,largestRectangleArea(height));
        }
        return ressult;
    }
}

JavaScript