题目描述

原题链接

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1：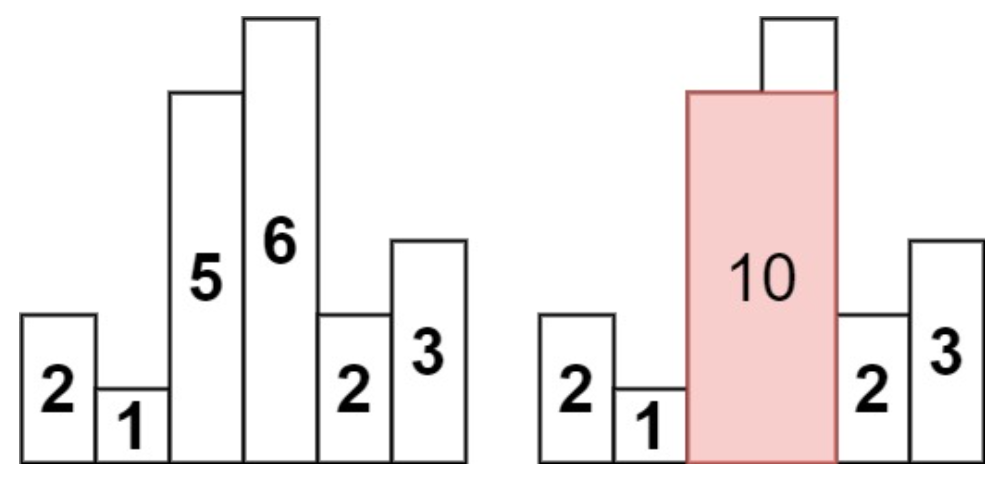

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

个人解法

Java

JavaScript

更优解法

Java

单调栈

暴力解法我们比较容易想到，我们只要找出每个柱子的左右边界（左右比自己低的第一个柱子或总的边界点）就可以计算出面积。但暴力解法会超时，我们需要优化，两侧的高都知道的话（左右边界确定），宽自然确定。我们首先考虑如何更好地确定左边界，右边界大同小异。
对于一个柱子来说，如果它左边的第一个柱子比自己矮，那这个柱子就是它的左边界。如果比自己高则继续往左找。

所以我们利用单调栈来解决问题，栈顶比自己小，直接记录左边界位置，自己入栈；栈顶比自己大，则弹出栈顶元素（找边界的边界（的边界）。。。。。。），一直到找到比自己小的元素，或到了边界-1。

class Solution {
 public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        //用于记录左右边界下标
        int[] left = new int[len];
        int[] right = new int[len];
        Stack<Integer> stack = new Stack<>();
     //用-1来表示边界
        stack.push(-1);
     //如果栈顶比自己小，直接记录左边界（栈顶）位置，自己入栈
        for (int i = 0; i < len; i++) {
            //栈顶比自己大，则弹出栈顶元素，一直到找到比自己小的元素
            while (stack.peek() != -1 && heights[i] <= heights[stack.peek()]) {
                stack.pop();
            }
            left[i] = stack.peek();
            stack.push(i);
        }
     //右边界寻找方法类似，不过右边界如果为最右边要存入len下标而不是-1
        stack = new Stack<>();
        stack.push(-1);
        for (int i = len-1; i >=0; i--) {
            while (stack.peek() != -1 && heights[i] <= heights[stack.peek()]) {
                stack.pop();
            }
            if (stack.peek()==-1){
                right[i]=len;
            }else {
                right[i] = stack.peek();
            }
            stack.push(i);
        }
        int max=-1;
     //遍历找到最大矩形
        for (int i=0;i<len;i++){
            max=Math.max(max,(right[i]-left[i]-1)*heights[i]);
        }
        return max;
    }
}

JavaScript