题目描述

原题链接
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

示例 1：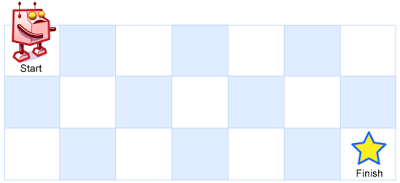
image.png
输入：m = 3, n = 7
输出：28

示例 2：
输入：m = 3, n = 2
输出：3
解释： 从左上角开始，总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下

示例 3：
输入：m = 7, n = 3
输出：28

示例 4：
输入：m = 3, n = 3
输出：6

提示：

  • 1 <= m, n <= 100
  • 题目数据保证答案小于等于 2 * 109

    个人解法

Javascript

DP

经典DP问题

  1. /*
  2.  * @lc app=leetcode.cn id=62 lang=javascript
  3.  *
  4.  * [62] 不同路径
  5.  */
  7. // @lc code=start
  8. /**
  9.  * @param {number} m
  10.  * @param {number} n
  11.  * @return {number}
  12.  */
  13. var uniquePaths = function (m, n) {
  14.   let dp = new Array(m);
  15.   for (let i = 0; i < m; i++) {
  16.     if (i === 0) {
  17.       dp[i] = new Array(n).fill(1);
  18.     } else {
  19.       dp[i] = new Array(n).fill(0);
  20.       dp[i][0] = 1;
  21.     }
  22.   }
  23.   for (let i = 1; i < m; i++) {
  24.     for (let j = 1; j < n; j++) {
  25.       dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
  26.     }
  27.   }
  28.   return dp[m - 1][n - 1];
  29. };
  30. // @lc code=end

递归

这题 DP 能解决的 递归也可以

不过很抱歉，这道题目递归是超时的！！！

  1. /*
  2.  * @lc app=leetcode.cn id=62 lang=javascript
  3.  *
  4.  * [62] 不同路径
  5.  */
  7. // @lc code=start
  8. /**
  9.  * @param {number} m
  10.  * @param {number} n
  11.  * @return {number}
  12.  */
  13. var uniquePaths = function (m, n) {
  14.   if (m === 1 || n === 1) {
  15.     return 1;
  16.   }
  17.   return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
  18. };
  19. // @lc code=end

Java

动态规划

  1. class Solution {
  2.     public int uniquePaths(int m, int n) {
  3.         int[][] dp=new int[m][n];
  4.         for (int i=0;i<m;i++){
  5.             dp[i][0]=1;
  6.         }
  7.         for (int j=0;j<n;j++){
  8.             dp[0][j]=1;
  9.         }
  10.         for (int i=1;i<m;i++){
  11.             for (int j=1;j<n;j++){
  12.                 dp[i][j]=dp[i-1][j]+dp[i][j-1];
  13.             }
  14.         }
  15.         return dp[m-1][n-1];
  16.     }
  17. }

其他解法

Java

image.png

  1. class Solution {
  2.     public int uniquePaths(int m, int n) {
  3.         long ans = 1;
  4.         for (int x = n, y = 1; y < m; ++x, ++y) {
  5.             ans = ans * x / y;
  6.         }
  7.         return (int) ans;
  8.     }
  9. }

Javascript

组合数学，直接看题解吧，不是很好理解
题解链接