题目描述

原题链接

给你一个链表数组，每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下： [ 1->4->5, 1->3->4, 2->6 ]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：
输入：lists = []
输出：[]

示例 3：
输入：lists = [[]]
输出：[]

提示：

  • k == lists.length
  • 0 <= k <= 10^4
  • 0 <= lists[i].length <= 500
  • -10^4 <= lists[i][j] <= 10^4
  • lists[i] 按 升序 排列
  • lists[i].length 的总和不超过 10^4

个人解法

Java(顺序合并）

  1. /**
  2.  * Definition for singly-linked list.
  3.  * public class ListNode {
  4.  *     int val;
  5.  *     ListNode next;
  6.  *     ListNode() {}
  7.  *     ListNode(int val) { this.val = val; }
  8.  *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
  9.  * }
  10.  */
  11. class Solution {
  12.     public ListNode mergeKLists(ListNode[] lists) {
  13.         if (lists.length==0){
  14.             return null;
  15.         }
  16.         ListNode l1=lists[0];
  17.         for(int i=1;i< lists.length;i++){
  18.             l1=mergeTwoLists(l1,lists[i]);
  19.         }
  20.         return l1;
  21.     }
  23.     public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
  24.         ListNode prehead = new ListNode(-1);
  26.         ListNode prev = prehead;
  27.         while (l1 != null && l2 != null) {
  28.             if (l1.val <= l2.val) {
  29.                 prev.next = l1;
  30.                 l1 = l1.next;
  31.             } else {
  32.                 prev.next = l2;
  33.                 l2 = l2.next;
  34.             }
  35.             prev = prev.next;
  36.         }
  38.         // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
  39.         prev.next = l1 == null ? l2 : l1;
  41.         return prehead.next;
  42.     }
  43. }

JavaScript

  1. /*
  2.  * @lc app=leetcode.cn id=23 lang=javascript
  3.  *
  4.  * [23] 合并K个升序链表
  5.  */
  7. // @lc code=start
  8. /**
  9.  * Definition for singly-linked list.
  10.  * function ListNode(val, next) {
  11.  *     this.val = (val===undefined ? 0 : val)
  12.  *     this.next = (next===undefined ? null : next)
  13.  * }
  14.  */
  15. /**
  16.  * @param {ListNode[]} lists
  17.  * @return {ListNode}
  18.  */
  19. var mergeKLists = function (lists) {
  20.   let listsArr = [];
  21.   let flag = true;
  22.   let root = new ListNode(0);
  23.   let temp = root;
  24.   const len = lists.length
  25.   for (let i = 0; i < len; i++) {
  26.     if (lists[i]) {
  27.       listsArr.push(lists[i]);
  28.     }
  29.   }
  30.   while (flag) {
  31.     const nowRootIndex = getMin(listsArr);
  32.     if (!listsArr.length) {
  33.       flag = false;
  34.       break;
  35.     }
  36.     temp.next = new ListNode(listsArr[nowRootIndex].val);
  37.     temp = temp.next;
  38.     listsArr[nowRootIndex] = listsArr[nowRootIndex].next;
  39.     if (listsArr[nowRootIndex] === null) {
  40.       listsArr.splice(nowRootIndex, 1);
  41.     }
  42.   }
  43.   return root.next;
  44. };
  45. function getMin(arr) {
  46.   let minIndex = 0;
  47.   const len = arr.length;
  48.   for (let i = 1; i < len; i++) {
  49.     if (arr[i] && arr[i].val < arr[minIndex].val) {
  50.       minIndex = i;
  51.     }
  52.   }
  53.   return minIndex;
  54. }
  55. // @lc code=end

其他解法

题解链接

Java

分治法

  1. class Solution {
  2.     public ListNode mergeKLists(ListNode[] lists) {
  3.         return merge(lists, 0, lists.length - 1);
  4.     }
  6.     public ListNode merge(ListNode[] lists, int l, int r) {
  7.         if (l == r) {
  8.             return lists[l];
  9.         }
  10.         if (l > r) {
  11.             return null;
  12.         }
  13.         int mid = (l + r) >> 1;
  14.         return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
  15.     }
  17.     public ListNode mergeTwoLists(ListNode a, ListNode b) {
  18.         if (a == null || b == null) {
  19.             return a != null ? a : b;
  20.         }
  21.         ListNode head = new ListNode(0);
  22.         ListNode tail = head, aPtr = a, bPtr = b;
  23.         while (aPtr != null && bPtr != null) {
  24.             if (aPtr.val < bPtr.val) {
  25.                 tail.next = aPtr;
  26.                 aPtr = aPtr.next;
  27.             } else {
  28.                 tail.next = bPtr;
  29.                 bPtr = bPtr.next;
  30.             }
  31.             tail = tail.next;
  32.         }
  33.         tail.next = (aPtr != null ? aPtr : bPtr);
  34.         return head.next;
  35.     }
  36. }

优先队列

  1. class Solution {
  2.     class Status implements Comparable<Status> {
  3.         int val;
  4.         ListNode ptr;
  6.         Status(int val, ListNode ptr) {
  7.             this.val = val;
  8.             this.ptr = ptr;
  9.         }
  11.         public int compareTo(Status status2) {
  12.             return this.val - status2.val;
  13.         }
  14.     }
  16.     PriorityQueue<Status> queue = new PriorityQueue<Status>();
  18.     public ListNode mergeKLists(ListNode[] lists) {
  19.         for (ListNode node: lists) {
  20.             if (node != null) {
  21.                 queue.offer(new Status(node.val, node));
  22.             }
  23.         }
  24.         ListNode head = new ListNode(0);
  25.         ListNode tail = head;
  26.         while (!queue.isEmpty()) {
  27.             Status f = queue.poll();
  28.             tail.next = f.ptr;
  29.             tail = tail.next;
  30.             if (f.ptr.next != null) {
  31.                 queue.offer(new Status(f.ptr.next.val, f.ptr.next));
  32.             }
  33.         }
  34.         return head.next;
  35.     }
  36. }

JavaScript

解法1——顺序合并

  1. /**
  2.  * @param {ListNode[]} lists
  3.  * @return {ListNode}
  4.  */
  5. var mergeKLists = function (lists) {
  6.   let temp = null;
  7.   const len = lists.length;
  8.   for (let i = 0; i < len; i++) {
  9.     temp = mergin(temp, lists[i]);
  10.   }
  11.   return temp;
  12. };
  13. function mergin(list1, list2) {
  14.   let node1 = list1;
  15.   let node2 = list2;
  16.   const root = new ListNode();
  17.   let temp = root;
  18.   while (node2 && node1) {
  19.     if (node1.val <= node2.val) {
  20.       temp.next = node1;
  21.       node1 = node1.next;
  22.     } else {
  23.       temp.next = node2;
  24.       node2 = node2.next;
  25.     }
  26.     temp = temp.next;
  27.   }
  28.   temp.next = node1 ? node1 : node2;
  29.   return root.next;
  30. }

解法二——分治合并

考虑优化方法一，用分治的方法进行合并。
将 k 个链表配对并将同一对中的链表合并；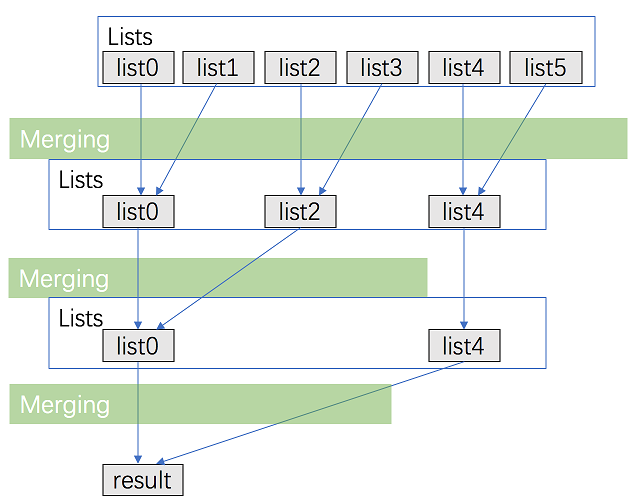
image.png
重复这一过程，直到我们得到了最终的有序链表。

  1. /**
  2.  * @param {ListNode[]} lists
  3.  * @return {ListNode}
  4.  */
  5. var mergeKLists = function (lists) {
  6.   if (!lists.length) {
  7.     return null;
  8.   }
  9.   let len = lists.length;
  10.   let arr = lists;
  11.   while (len > 1) {
  12.     let temp = null;
  13.     let tempArr = [];
  14.     let length = arr.length;
  15.     for (let i = 0; i < length; i += 2) {
  16.       if (i + 1 < length) {
  17.         temp = mergin(arr[i], arr[i + 1]);
  18.         tempArr.push(temp);
  19.       } else {
  20.         tempArr.push(arr[i]);
  21.       }
  22.     }
  23.     arr = [...tempArr];
  24.     len /= 2;
  25.   }
  26.   return arr[0];
  27. };
  28. function mergin(list1, list2) {
  29.   let node1 = list1;
  30.   let node2 = list2;
  31.   const root = new ListNode();
  32.   let temp = root;
  33.   while (node2 && node1) {
  34.     if (node1.val <= node2.val) {
  35.       temp.next = node1;
  36.       node1 = node1.next;
  37.     } else {
  38.       temp.next = node2;
  39.       node2 = node2.next;
  40.     }
  41.     temp = temp.next;
  42.   }
  43.   temp.next = node1 ? node1 : node2;
  44.   return root.next;
  45. }
  1. class Solution {
  2.     public ListNode mergeKLists(ListNode[] lists) {
  3.         return merge(lists, 0, lists.length - 1);
  4.     }
  6.     public ListNode merge(ListNode[] lists, int l, int r) {
  7.         if (l == r) {
  8.             return lists[l];
  9.         }
  10.         if (l > r) {
  11.             return null;
  12.         }
  13.         int mid = (l + r) >> 1;
  14.         return mergeTwoLists(merge(lists, l, mid), merge(lists, mid + 1, r));
  15.     }
  17.     public ListNode mergeTwoLists(ListNode a, ListNode b) {
  18.         if (a == null || b == null) {
  19.             return a != null ? a : b;
  20.         }
  21.         ListNode head = new ListNode(0);
  22.         ListNode tail = head, aPtr = a, bPtr = b;
  23.         while (aPtr != null && bPtr != null) {
  24.             if (aPtr.val < bPtr.val) {
  25.                 tail.next = aPtr;
  26.                 aPtr = aPtr.next;
  27.             } else {
  28.                 tail.next = bPtr;
  29.                 bPtr = bPtr.next;
  30.             }
  31.             tail = tail.next;
  32.         }
  33.         tail.next = (aPtr != null ? aPtr : bPtr);
  34.         return head.next;
  35.     }
  36. }