题目描述

原题链接

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：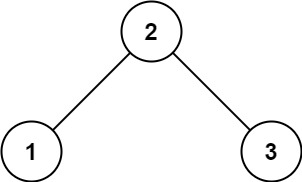

输入：root = [2,1,3]
输出：true

示例 2：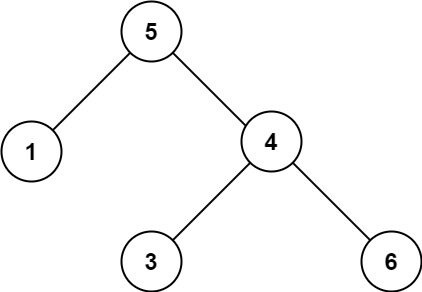

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

  个人解法

Javascript

/*
 * @lc app=leetcode.cn id=98 lang=javascript
 *
 * [98] 验证二叉搜索树
 */
// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
 const check = function (root, min = -Number.MAX_VALUE, max = Number.MAX_VALUE) {
  let leftRes = false;
  let rightRes = false;
  if (root.val < max && root.val > min) {
    if (root.left === null) {
      leftRes = true;
    } else {
      leftRes = root.left.val < root.val && check(root.left, min, root.val);
    }
    if (root.right === null) {
      rightRes = true;
    } else {
      rightRes = root.right.val > root.val && check(root.right, root.val, max);
    }
  }
  return leftRes && rightRes;
}
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isValidBST = function (root) {
  return check(root);
};
// @lc code=end

简化了一下

const helper = (root, lower, upper) => {
    if (root === null) {
        return true;
    }
    if (root.val <= lower || root.val >= upper) {
        return false;
    }
    return helper(root.left, lower, root.val) && helper(root.right, root.val, upper);
}
var isValidBST = function(root) {
    return helper(root, -Infinity, Infinity);
};

Java

递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isValidBST(TreeNode root) {
        return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
    public boolean isValidBST(TreeNode node, long lower, long upper) {
        if (node == null) {
            return true;
        }
        if (node.val <= lower || node.val >= upper) {
            return false;
        }
        return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);
    }
}

中序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> tree=new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        inorderTraversal(root,1);
        return tree;
    }
    public void inorderTraversal(TreeNode root,int n) {
        if (root==null){
            return ;
        }
        inorderTraversal(root.left,0);
        tree.add(root.val);
        inorderTraversal(root.right,0);
    }
    public boolean isValidBST(TreeNode root) {
        List<Integer> result= inorderTraversal(root);
        for (int i=0;i<result.size()-1;i++){
            if (result.get(i)>=result.get(i+1)){
                return false;
            }
        }
        return true;
    }
}

其他解法

Java

中序遍历优化版

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    long pre = Long.MIN_VALUE; // 记录上一个节点的值，初始值为Long的最小值
    public boolean isValidBST(TreeNode root) {
        return inorder(root);
    }
    // 中序遍历
    private boolean inorder(TreeNode node) {
        if(node == null) return true;
        boolean l = inorder(node.left);
        if(node.val <= pre) return false;
        pre = node.val;
        boolean r = inorder(node.right);
        return l && r;
    }
}

Javascript

中序遍历

题解链接

判断二叉树的中序遍历结果是否是有序的，如果是有序的，那么就是一个二叉搜索树

var isValidBST = function(root) {
    let stack = [];
    let inorder = -Infinity;
    while (stack.length || root !== null) {
        while (root !== null) {
            stack.push(root);
            root = root.left;
        }
        root = stack.pop();
        // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树
        if (root.val <= inorder) {
            return false;
        }
        inorder = root.val;
        root = root.right;
    }
    return true;
};