首先在阿里一面的时候被问了逻辑斯蒂回归与SVM有什么异同然后我说我不知道,然后就看了一下这两个东西,顺便学了一下瓜皮书里根本看不懂的SVM。
逻辑斯蒂回归
逻辑斯蒂回归常用于二分类问题,属于判别模型的一种,它将样本空间的实值压缩成了一个0-1之间的小数:

逻辑回归的输出是有概率含义的,它的输出结果表达的是当前测试样本属正类的概率。由上式可以推导出:

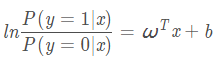
支持向量机
https://zhuanlan.zhihu.com/p/49331510
这个是真的讲的很详细!
对于支持向量机,数据点若是p维向量,我们用p-1维的超平面来分开这些点。但可能有许多超平面可以把数据分类,最佳超平面的合理选择就是以最大间隔把两个类分开的超平面。因此,SVM选择能够使离超平面最近的数据点的到超平面距离最大的超平面。
支持向量机从简单到复杂,可分为以下三类:
线性可分SVM:
训练数据线性可分,可通过硬间隔最大化学习得到线性分类器;
线性SVM:
训练数据非线性可分,通过软间隔最大化学得线性分类器;
非线性SVM:
训练数据线性不可分,通过使用核技巧和软间隔最大化,学得非线性SVM。
SVM基本原理
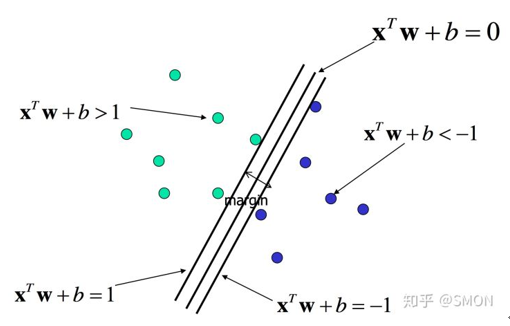<br />考虑一线性可分的训练数据集:**Xi**是一个列向量,**yi**是标量(y∈+1,-1),**yi**=+1时表示属于正类别,**yi**=-1时表示属于负类别。训练集中正例**Xi·w**+b>1,反例**Xi·w**+b<-1。<br /> 对于**x·w**+b=0,将求解两条平行直线的距离公式推广至高维:<br /> 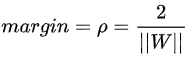<br />支持向量机的求解过程就是求解出使得margin最大的分割线,以使得类间距最大化,即选择满足条件的分割线中**||w||**最小的分割线。
支持向量
在线性可分的情况下,训练数据集的样本点中与分离超平面距离最近的数据点称为支持向量,即满足关系式yi*(XiW+b)=1的样本点。
在决定最佳超平面时只有支持向量起作用,而其他数据点并不起作用。如果移动非支持向量,甚至删除非支持向量都不会对最优超平面产生任何影响。也即支持向量对模型起着决定性的作用,这也是“支持向量机”名称的由来。
### 求解分离超平面是个纯数学过程,见知乎文章。
线性SVM——软间隔
很多时候数据集都不会理想到线性可分,解决该问题的一个办法是允许SVM在少量样本上出错,即将之前的硬间隔最大化条件放宽一点,为此引入“软间隔”的概念。即允许少量样本不满足约束yi*(XiW+b)≥1。
为使不满足上述条件的样本点尽可能少,我们需要在优化的目标函数里新增一个对这些点的惩罚项。最常用的是hinge损失(合页损失):


此时优化目标转变为:

其中C是一个超参数,称为惩罚参数。C太小会导致欠拟合,C太大会导致过拟合。
非线性SVM——核技巧
对于非线性的问题,需要用核技巧将线性支持向量机推广到非线性支持向量机。需要注意的是,不仅仅是SVM,很多线性模型都可以用核技巧推广到非线性模型,例如核线性判别分析(KLDA)。
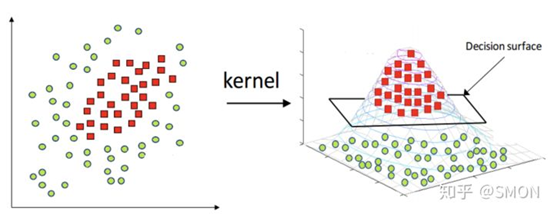
核函数的定义非常复杂,详细的可以看知乎那篇文章。
SVM的优缺点
优点:
- SVM是一个凸优化问题,所以求得的解一定是全局最优而不是局部最优。
- 不仅适用于线性线性问题还适用于非线性问题(用核技巧)。
- 拥有高维样本空间的数据也能用SVM,这是因为数据集的复杂度只取决于支持向量而不是数据集的维度, 这在某种意义上避免了“维数灾难”。
- 理论基础比较完善(不像神经网络就更像一个黑盒子)。
缺点:
- 二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可 以缓解这个问题)。
- 只适用于二分类问题。(SVM的推广SVR也适用于回归问题;可以通过多个SVM的组合来解决多分类问题。
SVM和逻辑斯蒂回归的异同
异:
- LR和SVM都是分类算法,常用于二分类。
- SVM只考虑局部的,边界附近的点(支持向量),而LR考虑全局。
- LR和SVM都是监督学习。
- LR和SVM都是判别模型。
同:
- LR的输出是连续的,而SVM是离散的。
- LR常用交叉熵作为损失,而SVM的损失函数包括“结构风险”和“经验风险”两部分。
- 线性SVM依赖数据表达的距离测度,需要做正则化,LR不受影响。
- 解决非线性问题时,SVM采用核函数,LR常常不采用(SVM只考虑少数样本,LR考虑全局计算量爆炸)
常见的判别模型
SVM、LR、隐马尔可夫场、贝叶斯网络、KNN、马尔科夫随机场(MRF)


