对DNN本质的探索

将ResNet视为浅网络的集合

《Residual Networks Behave Like Ensembles of Relatively Shallow Networks》
论文：https://arxiv.org/pdf/1605.06431.pdf

该文主要有三点贡献：

1. 从独特的视角，将ResNet视为浅网络的集合；
2. 实验表明了ResNet的这些浅网络（浅的paths）相互之间相关性不强，即使它们是联合训练的。裁Block后的网络的性能取决于剩余有效路径的数量；
3. 研究了不同长度的path中梯度的流动情况，实验表明了非常深的路径对训练没有贡献。

出发点

同样是一个ResNet结构的网络，我们可以将其展开为个子网络，其中为ResNet的Block数量（如果忽视短连接数据流中的ReLU）：

如下图所示。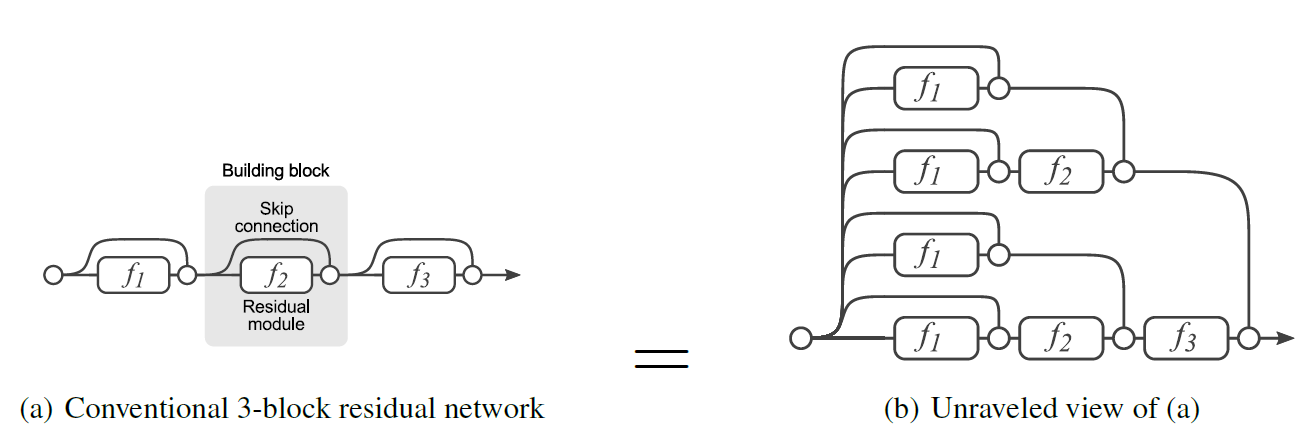

一旦将ResNet视为子网络的集合，就可以将最终的推理结果理解成所有子网络的集成。

实验论证

裁单个Block

对于残差网络，删除一个Block（只留下短连接）相当于删除整个网络中一半的路径；而对于直筒网络，删除一个Block会切断所有原有的数据流。

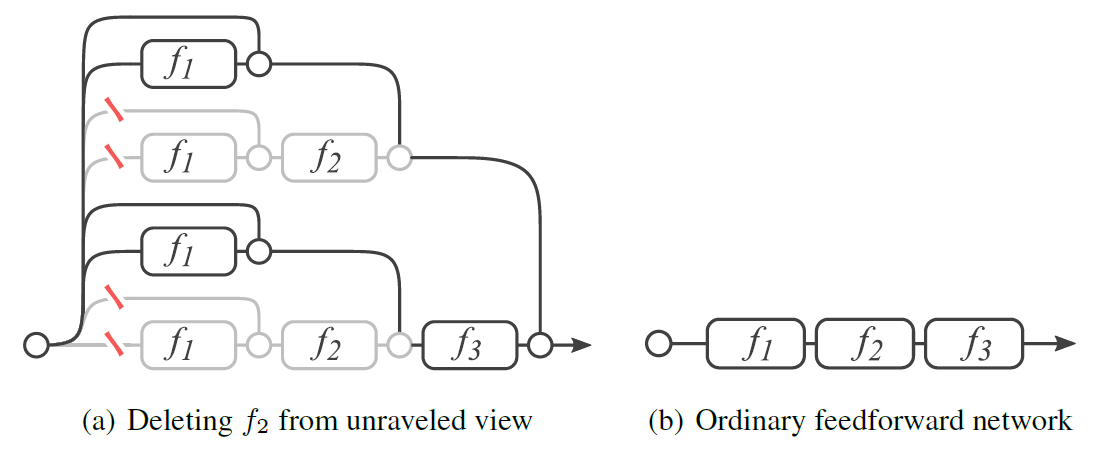
作者在CIFAR10数据集上对比了ResNet110和VGG15网络，如果只删除一个Block，在不finetune的情况下，VGG15毫不意外地直接炸成了随机输出，但ResNet竟然是几乎不掉点的（除了每个stage的第一层）。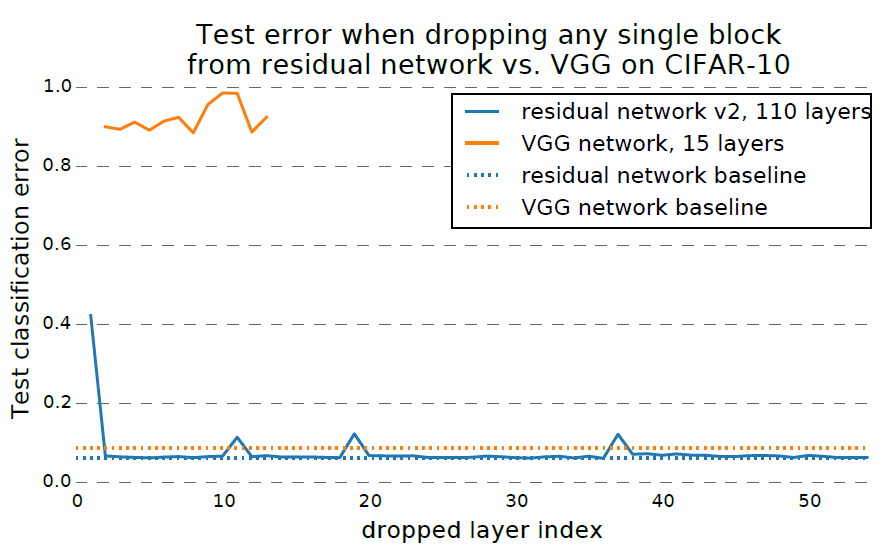

自己在CIFAR100上做的ResNet110和ResNet56的实验类似，不过比较神奇的是裁某些深层的Block虽然会导致准确度下浮下降，但是会导致测试集上的交叉熵loss暴跌，非常神奇。。


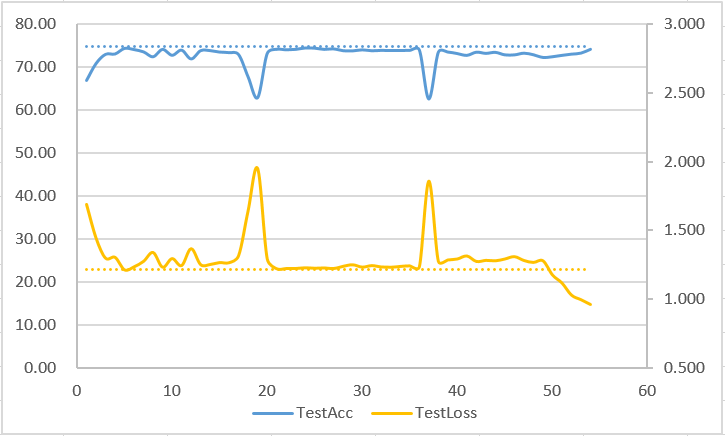
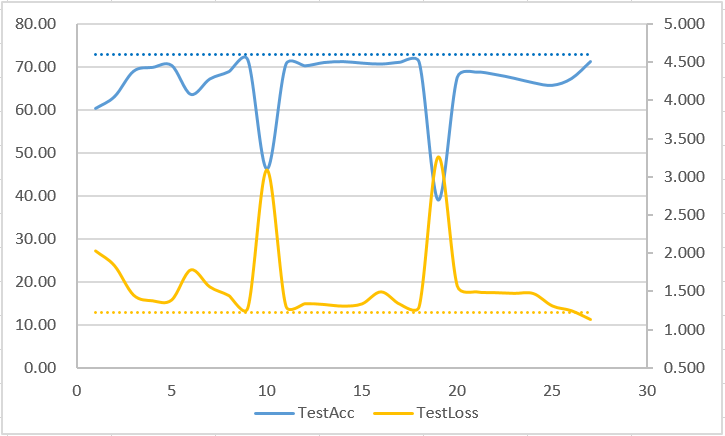
不过进一步把网络缩小换成ResNet20时，不管裁哪个Block，loss和准确度全部会炸的亲妈爆炸，坏的情况直接蜕化为接近随机输出，好的情况还能保持40%多的准确率。

裁多个Block/打乱Block顺序

作者进一步裁了多个Block，甚至打乱了Block顺序进行实验，结果表明模型的性能与剩余有效路径数量有关。譬如对于ResNet110，原始的有效路径数量为条，裁掉10个Block都还有条。
（衡量两个排序序列相似度的指标：Kendall Tau correlation，肯德尔相关系数）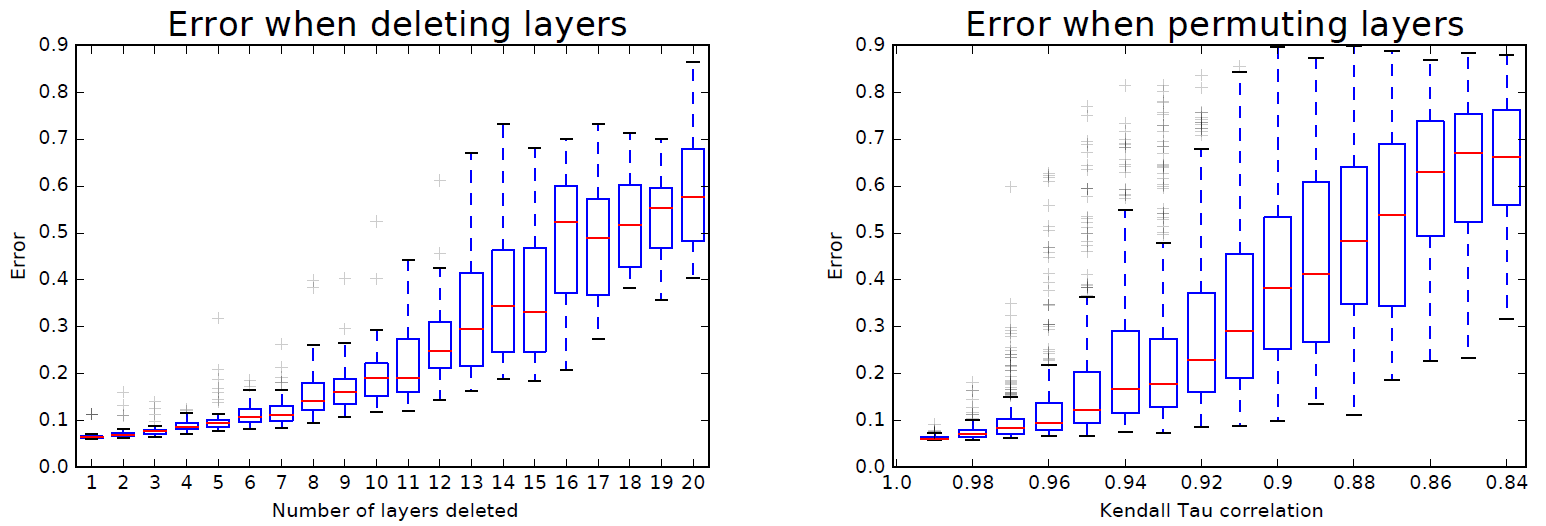

路径长度的分布

ResNet中每个Block都有残差和短连接两个分支，因此ResNet中路径长度的分布状况符合二项分布。对于Block数量为54的ResNet110而言，95%以上的路径长度分布在19~35Block之间，如下图（左）所示。
在早期的VGG网络中，浅层梯度比深层小的现象非常严重，即使BN的提出缓解了这一问题。作者在预训练的ResNet110中随机采样了单条不同长度的路径（第一节中我们提到的所谓子网络），即每个Block只有残差或者短连接中的一条通路。然后观察loss随着这条路径反传到input时的梯度，发现即使有BN的存在，依然是越深的路径回传到input处梯度越小，且梯度大小随着路径变深呈指数级别变小，如下图（中）所示。
比较有趣的是，如果我们把不同长度的路径，其路径数量与梯度大小各自相乘并绘制出其分布状态，得到下图（右）所示，可以发现长度大于20的路径（子网络）对梯度的贡献是微乎其微的。而长度为5~17Block的路径，即使只占据了所有路径数量的0.45%，却贡献了极大部分的梯度信息。
这也点了这篇论文的中心思想：the effective paths are relatively shallow !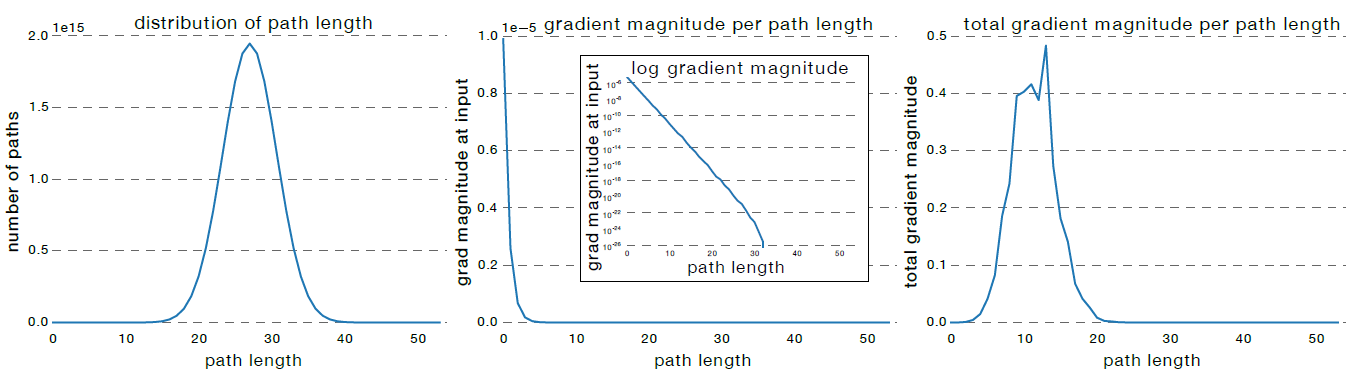

作者做了另一个实验，对于ResNet110，每个batch只随机取23个Block进行训练，在CIFAR10上达到了5.96%的准确率，超越了6.10%的baseline。（不过这样不就是Stochastic Depth了么？？？）

彩票定理

《THE LOTTERY TICKET HYPOTHESIS: FINDING SPARSE, TRAINABLE NEURAL NETWORKS》
论文：https://arxiv.org/pdf/1803.03635.pdf

这篇论文其实说白了就一句话：不同初始化决定了裁不同的神经元后网络会表现更好，裁剪更重要的是获取网络结构而非继承训练后的参数。作者也将这些针对给定的初始化数值裁剪得到的结构成为“Lottery Ticket”，即“彩票”。即使将裁剪后的网络从头开始训也能获得非常好的效果，其关键点在于：裁剪后的网络必须继承原始网络的初始化数值。
作者提出的寻找彩票的步骤如下所示：

1. 随机初始化网络，其中的初始化符合；
2. 训练网络个step后，得到参数；
3. 建立掩膜，裁掉一部分中的参数；
4. 用重新初始化裁剪后的子网络；
5. 重复2~4步直到裁剪率符合预期。

论文的精髓体现在第4步，如果不用原始网络的初始化数值初始化裁剪后的网络，那么即使是“彩票网络”也会表现的非常差。作者也同样实验论证了，采用one-shot一次性裁剪的网络即时应用彩票定理表现的很差。
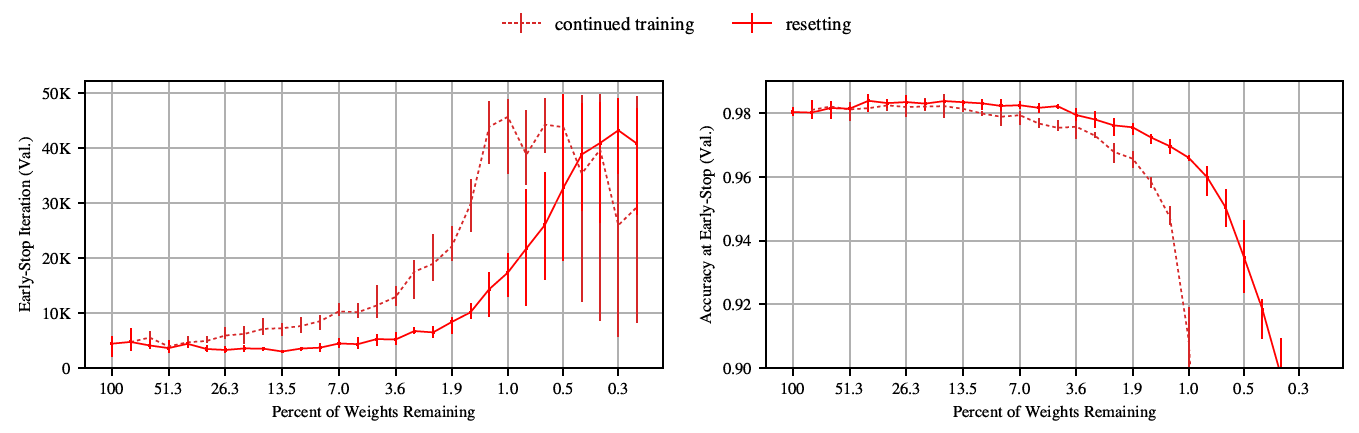
下图左展示了网络训收敛需要的step数量，可以看到随着裁剪率的变大，网络会越来越难训，作者将其解释为重度裁剪后的稀疏网络包含的“彩票”数量少。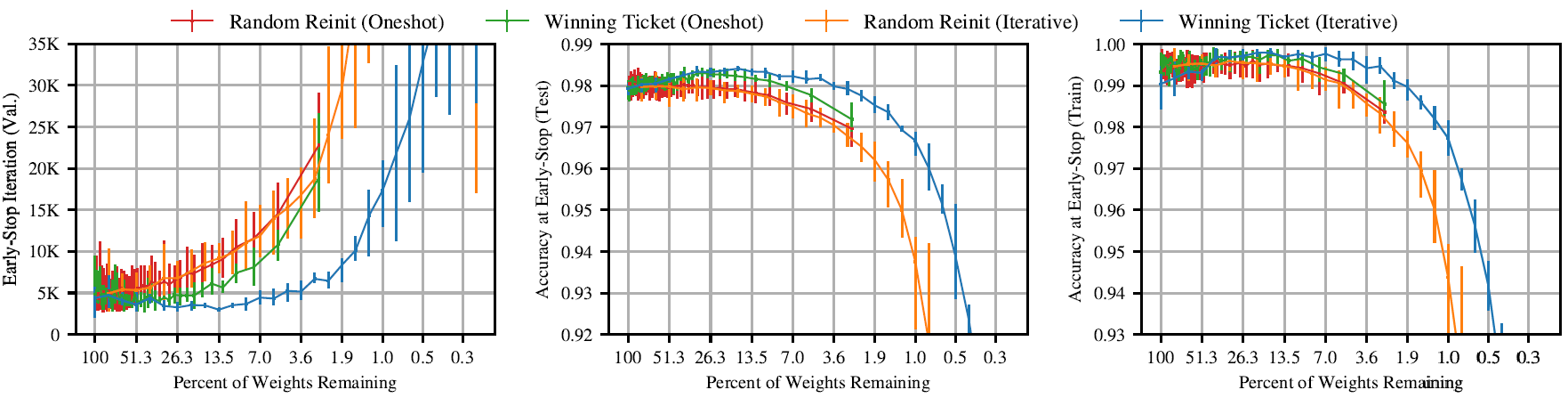

作者做MNIST和Conv2/4/6的Toy Model实验的时候是裁掉每层的参数，而做VGG和ResNet实验的时候是裁整个网络最小的参数的，因为每层的参数量、冗余度、重要程度都不同。
但是作者发现在VGG、ResNet这种正常模型上找“彩票”非常困难，需要深度学习调参，改schedule。作者得出的超参在VGG上是0.1的学习率warmup 10K步，ResNet18上得出的超参是0.03的学习率warmup 20K步（0.1的初始学习率怎么都学不好）。

Appendix

每次裁完开始下一iteration的时候是用原始网络的初始化数值初始化裁剪后的网络，还是继承训好的权重？实验表明还是reset更好——进一步表明了裁剪更多的是为了获取网络结构而非训好的权重。