谷歌白皮书解读
谷歌白皮书:https://blog.csdn.net/guvcolie/article/details/81286349
但是郑老师说里面有不少东西都过时了,甚至有一些可能是写错的了?
1. 模型量化大大滴好
但与输入图片直接接触的第一个卷积层通常不参与量化,量化第一个层会造成精度的剧烈下降。
2.1 非对称量化
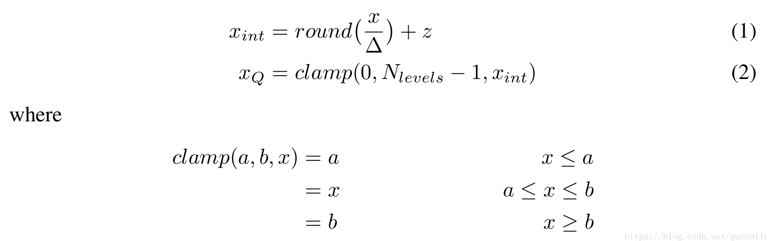<br />郑老师说现在非对称量化几乎不用了,NVIDIA也说非对称量化大大滴坏。<br />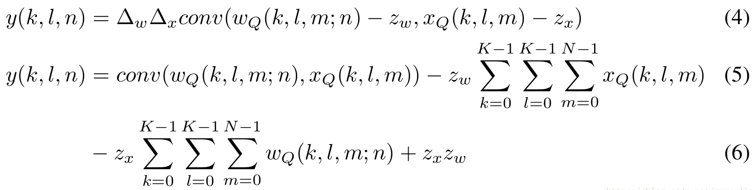<br />其中K为kernal_size(对于3x3卷积那么K=3),N为通道数,n代表mini-batch中的每一个sample。
(6)式中最后的ZxZw应该是,原文写错了。由于引入了bias项zx和zw,在实际以int8形式计算卷积后,还原成float32的时候多出了3项,会导致计算带来很多麻烦,所以零点对应是很有好处的,即float32的零值对应int8/uint8的零值。
2.2 对称量化
对称量化只有scale项,没有bias。我也不知道为什么原文里说用SIMD的时候钳位要多限制一个level,郑老师说现在大家都用0-255,不知道底层硬件怎么在做的。
2.4 反传中的模拟量化
在感知量化的训练过程中,我们对x和w均采用模拟量化操作,即量化后再紧跟一个反量化。由于模拟量化过程不可导,我们需要在反传阶段构建一个模拟量化过程,即“直通估计器”。

2.5 确定量化scale
《Deep Compression》中作者通过K-Means聚类获取量化中心,这样精度确实高,但是一来不是线性量化,推理的时候依赖表项,严重的访存不友好;二来K-Means的开销非常大,VGG16中对4096*4096的全连接层进行聚类更是需要一个小时。
这里我们着重讨论最简易的线性量化,它可以不依赖于表项进行推理(相比于K-Means),只需要知道scale就行了。比较简单的方法,对于权重直接根据最大绝对值取scale;对于激活,取跨批最大绝对值的滑动平均作为scale(一般100batch就够了)。
对于激活输出的量化,TensorRT通过最小化原始数据分布和量化后数据分布之间的KL散度来确定scale。
基于KL散度的离线量化(非感知量化)
参考:http://on-demand.gputechconf.com/gtc/2017/presentation/s7310-8-bit-inference-with-tensorrt.pdf
KL散度衡量的是两个随机分布的偏离程度,可是量化前后的数据是样本的一系列连续值,需要归到离散的cluster中才能算KL。一般取cluster数量为2048,基于一层中一部分激活输出的最大值确定cluster对应值的上界,并在所有cluster上对值进行线性划分。(郑老师的代码里直接取第一个batch前向激活输出的最大值)
原始分布直接拉区间算概率就行,量化后的值归到cluster以后只有256个cluster有值,需要对剩下的cluster进行插值(↑到/\的插值,相邻8cluster均匀插值等)。谷歌提出基于KL散度量化的时候是采用均匀分布的,同时插值时需要保持原始分布中为0的cluster在量化插值后依然为0,郑老师说使用谷歌的方法校准不好,用了<↑到/>的插值。谷歌的插值方法处理原始分布中为0的cluster时需要将这部分值匀到其它相关cluster,郑老师在<↑到/>中没用。
Input: FP32 histogram <H> with 2048 binsINT quantize levels count <levels>best = -1minKL = inffor upbound_bin in range(levels, 2048) #(0, upbound_bin)处的bin为量化范围, 之外的发生截断P = H[0:upbound_bin]outliers_cnt = sum(H[upbound_bin:2048])P[upbound_bin-1] += outliers_cntP /= sum(P)Q = quantize(P, levels) # 统计量化后的数据分布Q = interpolation(levels, upbound_bin) # 将量化后的分布插值至·upbound_bin· clusterQ /= sum(Q)if KL(P, Q) < minKL:minKL = KL(P, Q)best = upbound_binscale = (upbound_bin + 0.5) * width_of_bin / levels
2.6 量化的粒度
量化的粒度可分为逐层量化、逐通道量化。
对于激活输出量化,逐通道量化会使得计算变得非常麻烦——计算一个输出通道的值涉及到所有C个输入通道,但是每计算一个输入通道就需要进行一次逆量化。
激活输出采用逐层量化时,不同权重量化方法的结果(Asymmetric为非对称,Symmetric为对称):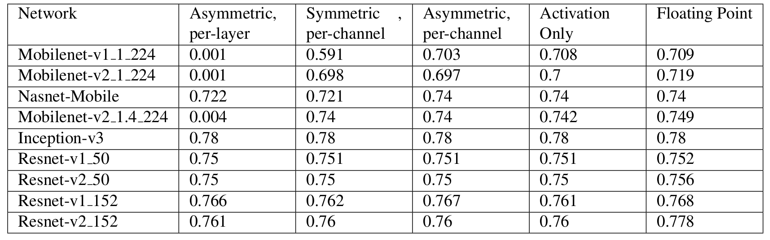
MobileNet因为用了深度可分离卷积,3*3卷积中各个输出通道之间互不关联,权重的分布可能大不相同,因此采用逐层量化权重时会原地爆炸。
几乎所有的量化精度损失都是源于权重量化。
3.2 感知量化
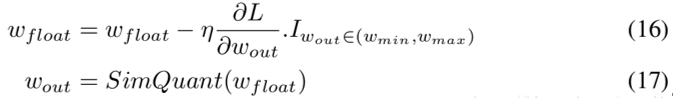<br />参数的训练**更新是在float型的参数上完成的**,但是**计算梯度需要根据模拟量化**的参数。其中是一个0/1函数,是模拟量化函数的求导过程。由于模拟量化的函数是锯齿状的,无法求导,为了能够保证反向传播需要构建近似量化用于求取梯度,如下图右所示。<br /> 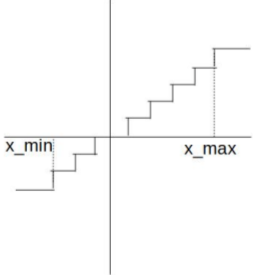 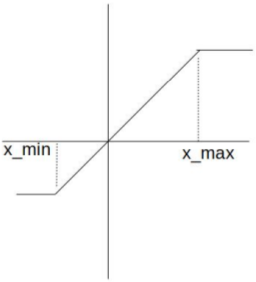<br />训练过程中采用模拟量化,即量化后马上把scale乘回来。模拟量化一般在权重层的一开始进行而不是在权重层的最后(ReLU后)进行。权重层开始时,将均进行模拟量化(模拟量化完依然是fp32)。对于有BN的网络,训练阶段对权重量化不能量化W,而要量化,且其scale在训练阶段每个batch需要独立计算。<br /> 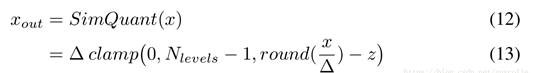<br />在推理阶段,BN层被融入了卷积层,直接被乘进了。和均为int8(如果激活函数用ReLU,x可以用uint8表示;但如果考虑架构通用性通常还是会用int8),相乘得到的结果会被累加在int32中。卷积完成后,将结果从int32转为fp32,乘上fp32的,再加上fp32的,ReLU后输出。<br />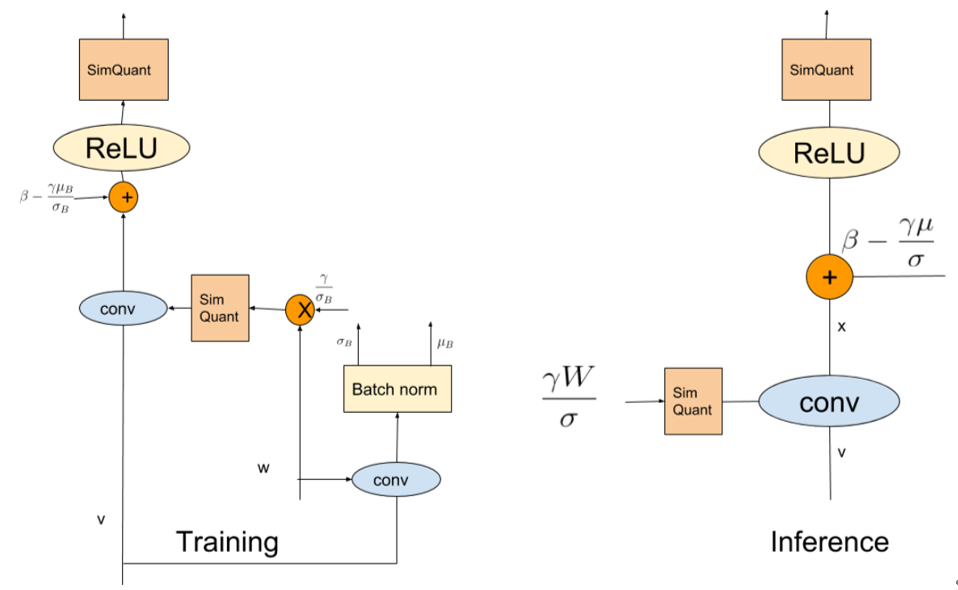
感知量化中的BN
在推理阶段BN是被融入卷积层的,但是我们必须在训练阶段就将BN融入卷积层。为了将BN融入卷积,我们需要事先获取当前batch的统计均值与统计方差,因此训练阶段每个卷积层的卷积操作需要做两遍,第一次卷积操作只是为了得到统计均值与统计方差后,将BN融入卷积权重进行第二次卷积操作得到输出。
这么做由于每个卷积要做两次,训练耗时直接翻倍,如果训练阶段不将BN融入卷积,推理阶段照旧会怎样?
推理阶段BN层后的值是量化以后的,如果训练阶段在经过虚拟卷积以后,卷积的结果直接以float形式输出,训练阶段的BN层就没有被量化,会与推理阶段不符。另外这样导致训练和推理阶段的网络逻辑结构不同?
在训练阶段,BN会使用batch批统计信息,而在预测阶段使用的是running_mean和running_var。由于批统计量在每个batch批之间变化很大,这会在量化的权重中引入不希望的跳变,也会是量化模型的精度降低。图重构也是一种解决方法,它可以消除训练和预测时bn的差异(如下图)。充分训练以后(20w-30w step),可采用running_mean和running_var进行训练,并冻结running_mean和running_var的更新。
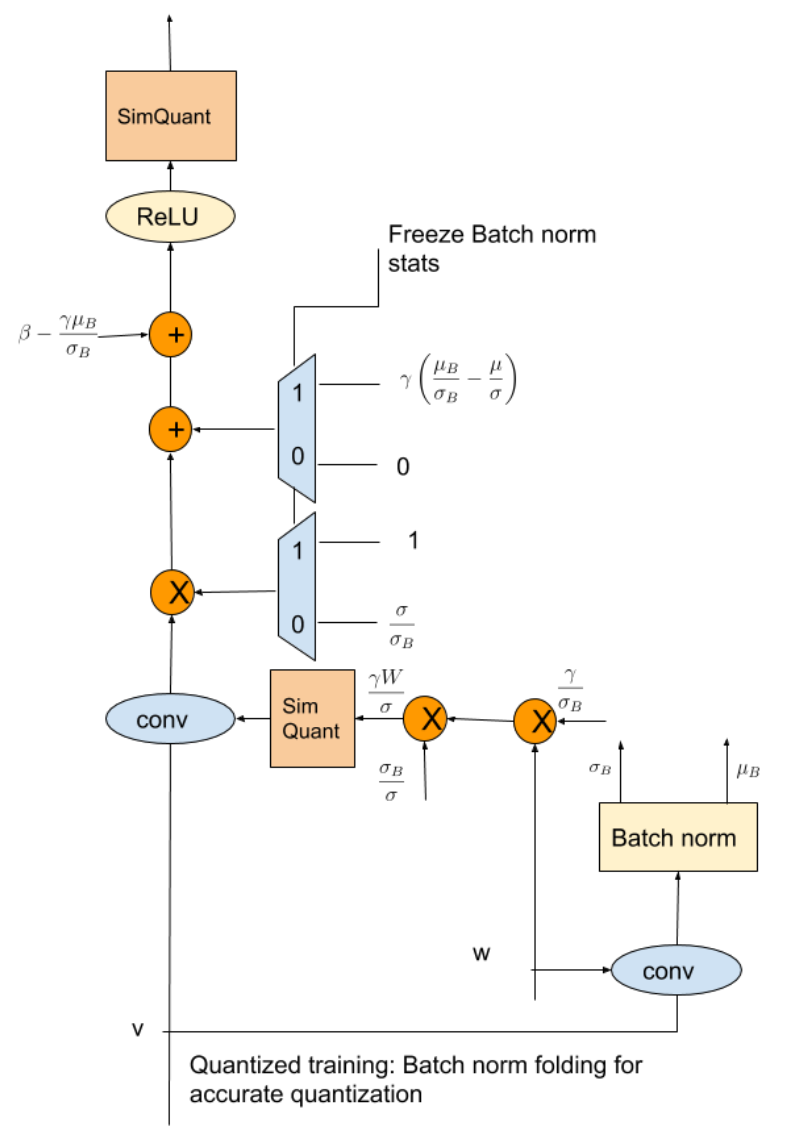
遗留问题
训练阶段不做两次卷积,预测直接融BN会怎样?
答:不怎么样,现在很多方法QAT都是全程用running_mean和running_var,不需要做两次卷积。
郑老师的代码全程用running_mean和running_var,和正常做法比有什么区别?
答:不怎么样,现在很多方法QAT都是全程用running_mean和running_var,做两次卷积取统计量的方法在低比特量化的时候反而会不稳定,造成模型爆炸、显卡爆炸乃至地球爆炸的后果。

