构建网络的构造空间

论文：https://arxiv.org/pdf/2003.13678.pdf
官方github：https://github.com/facebookresearch/pycls

感觉这篇论文的出发点确实非常新颖，看了以后有点打开了新世纪大门的感觉。这篇论文的思想有点像常用于围棋博弈AI的蒙特卡洛搜索，在不同的模型空间上随机采样N多次，然后选择表现好的那个模型空间。

网络构建空间

NAS成为了一种非常受欢迎的方法，它能够帮助我们在给定搜索空间（Search Space）中利用强化学习、遗传算法等方法中搜索到一个较优的网络结构。NAS的应用详见NAS网络搜索。
NASNet的搜索空间为Block内部的结构，空间大小为。
MnasNet的搜索空间为每个Block（类似于Stage）内堆叠的Layer结构与数量，空间大小为。
EfficientNet的搜索空间为缩放因子α、β、γ，空间大小非常小。
NAS-FPN的搜索空间为neck网络的连接方式，空间大小为。
SpineNet的搜索空间为backbone的Block顺序与连接方式，空间大小为。

本文提出的网络构建空间（Design Space）与上面说到的搜索空间（Search Space）其实是一回事，都是构成网络的若干选项构成的空间，但是本文却没有直接在整个空间中用NAS搜索，而是利用了一定的人工干预与经验，利用统计学方法，尽可能缩小构建空间，并使得缩小后的构建空间能够提供更加优秀的模型。

验证一个人工假设（譬如每次下采样后通道数应当变宽）的步骤：

1. 在原有构建空间的基础上，人工地提出一个限制条件，得到构建空间的一个子集。
2. 在和中分别随机采样个模型，进行训练并记录模型性能的概率分布。
3. 若明显优于，则能够证明是一个合理、正确的选项，否则驳回。

探索一个超参（譬如网络深度对性能的影响）的步骤：

1. 在构建空间上，采样个模型，进行训练并记录超参值与模型性能的键值对。
2. 从N个键值中随机采样25%的键值对，记录子集中损失最低的键值对对应的超参值。
3. 重复第2步10000次，得到10000个在25%样本上表现最佳的。
4. 构建使得最小化的的95%置信区间，取置信区间的中间值作为推测的最佳。

为了更快的实验速度，模型训练只在ImageNet上进行10epoch。

AnyNet的进化过程

X Block

AnyNet采用的基础Block结构非常类似于ResNet Bottleneck，但是有一定的不同，如下图所示。其中为ResNet Bottleneck中的expansion（通道收缩因子）；3x3卷积为分组卷积，每组宽度为，当时就是DW卷积。

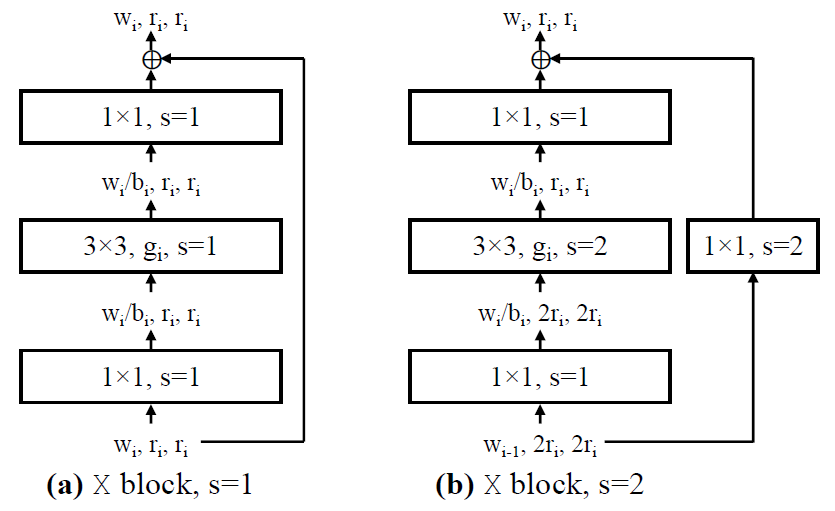
初始构造空间

输入分辨率恒定
总共4个stage，每个stage都有：
堆叠Block数
Block的输入/输出宽度
Bottleneck的通道收缩比例
3x3卷积采用分组卷积，每组的卷积宽度

若碰到的Block，则将当前Block的设为；
###若碰到且无法被整除，则将设为距离最近的，能被整除的值。

作者基于该初始构造空间构建了，它没有任何约束，只需要从初始构建空间中随机采样就行。作者在每次做验证时，都从构造空间中随机采样个小计算量的模型进行统计。注意这里的随机采样是以对数均匀分布（log-uniform）采样的（的概率密度是的两倍）！
初始构造空间的空间大小高达，与第一章里提到的利用NAS搜索的网络结构的搜索空间差不多大，但作者没有在这个搜索空间下进行NAS搜索，而是希望能利用人工干预与统计学方法，尽可能浓缩这个构造空间，并提高构造空间中模型的质量。
为了加速，样本只训10epoch，SGD(momentum=0.9)，bs=128，lr=0.05余弦衰减，wd=5e-5。

AnyNet

AnyNetX**A
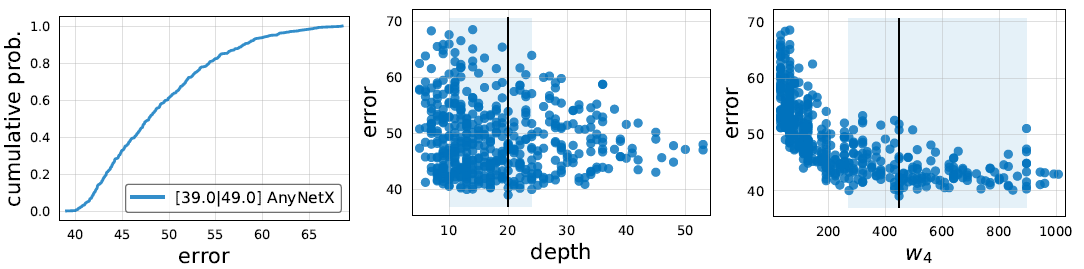
任何从初始构造空间中采样的网络，其性能概率分布如下图（左）所示。
另外作者还简单研究了网络的整体Block数（注意不是层数）、第4个stage的Block的输入/输出宽度对模型性能的影响，并用浅蓝色框标注了95%置信区间，如下图（中，右）所示。


AnyNetX**B~C
约束条件：所有的4个stage共享
为了减小搜索空间，作者尝试了让所有的4个stage共享通道收缩率，并以此缩小了初始构造空间得到了。作者做出了两个构造空间中模型的性能概率分布，可以看出两者几乎无差别。

约束条件：所有的4个stage共享
为了减小搜索空间，作者尝试了让所有的4个stage共享分组卷积宽度，并以此缩小了初始构造空间得到了。作者做出了两个构造空间中模型的性能概率分布，可以看出两者几乎无差别。

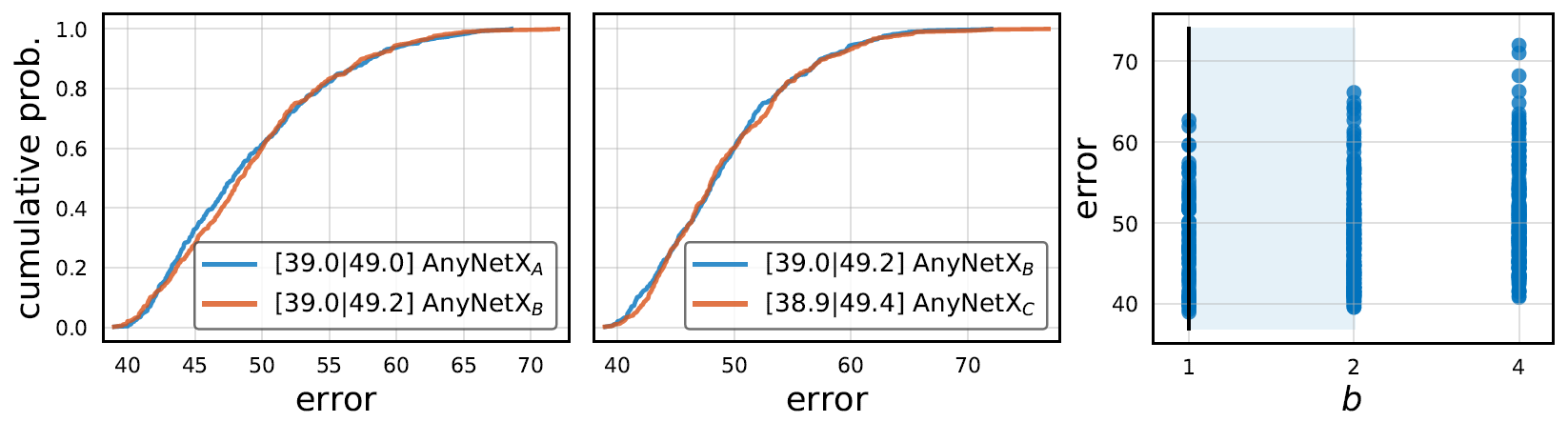
这么一来，作者就无损地缩小了原始构造空间为了，为后续研究提供了一定地便利，并且验证了经典地手工设计网络中让所有stage共享通道收缩率、分组卷积宽度的有效性。
作者还基于研究了收缩率对模型性能的影响，并用浅蓝色框标注了95%置信区间，如上图（右）所示，可以看出最佳的应有，为此作者反驳了ResNet Bottleneck采用的。（后面作者还追加实验表示MobileNet v2采用的Inverted Bottleneck的也非好的选择）

AnyNetX**D~E
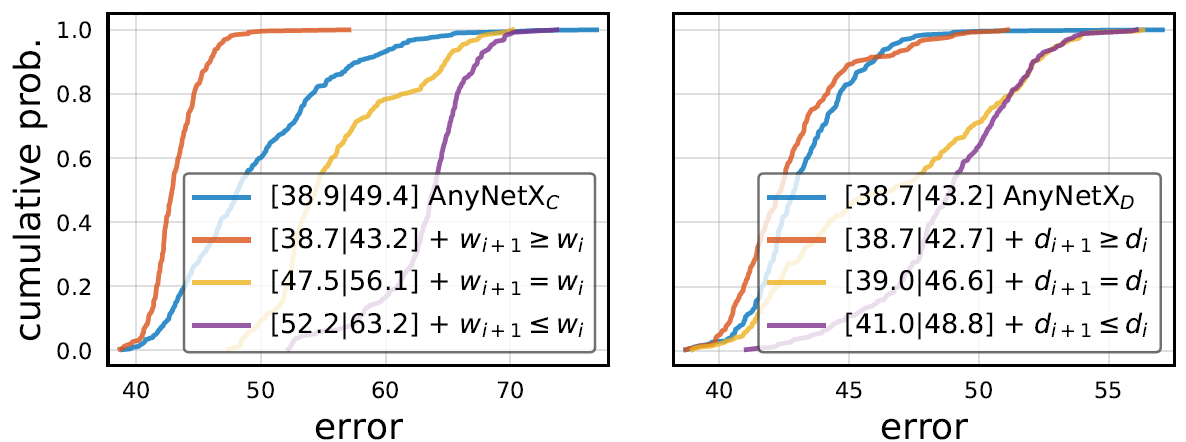
作者观察了中几个典型的性能较好的模型（下图上半部分）和性能较差（下图下半部分）的模型结构：

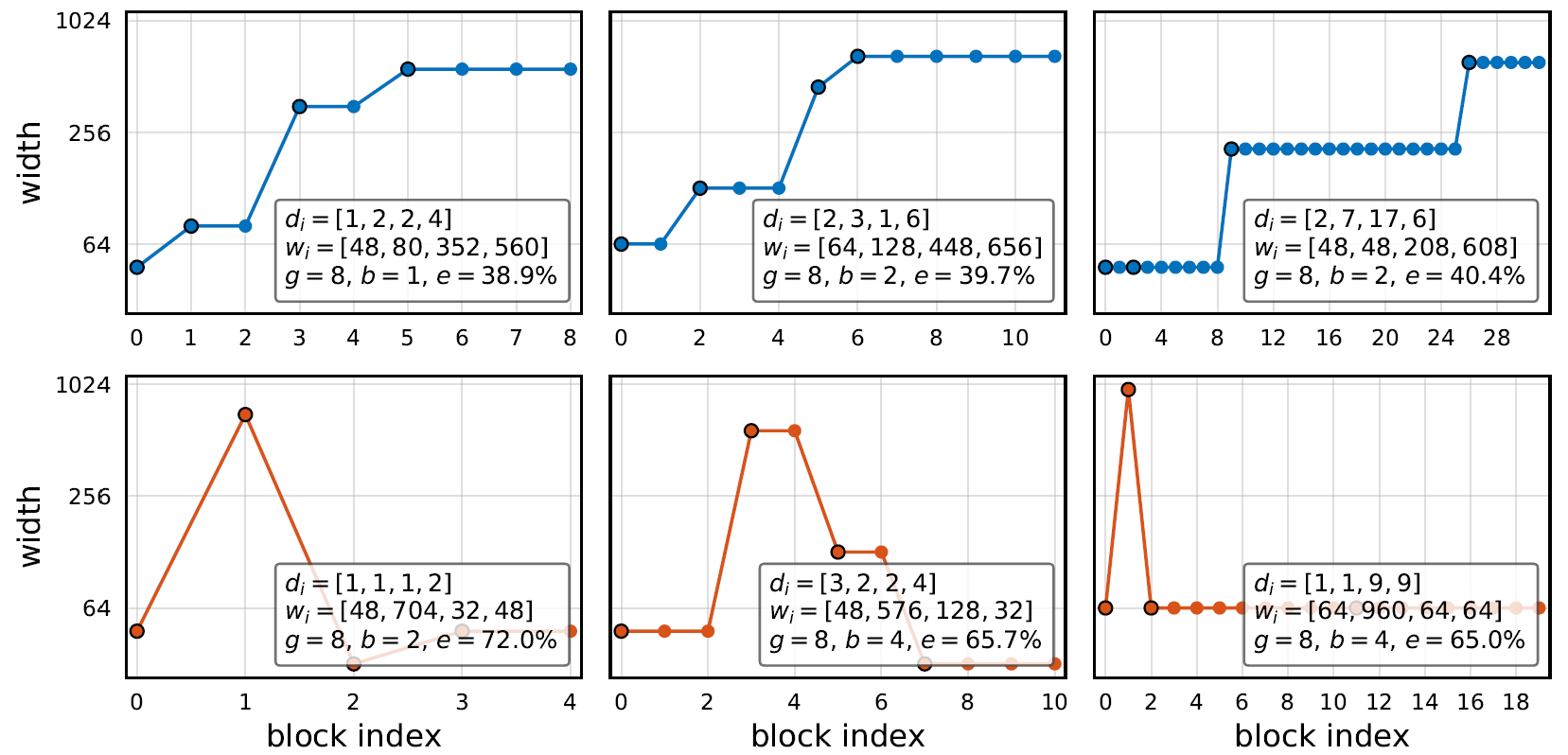
据此，作者提出了以下约束条件：
约束条件：**
这是一个非常经典的条件，约束每次下采样后网络宽度不能变小，从而得到了。可以看出这个约束条件极大地改善了模型性能。
通常的，为了使得不同stage的每一层计算量都近乎相等，我们都趋向于在每次下采样后将通道数扩为2倍，但这并不一定是最佳选择。

相对的，作者也研究了每个stage深度的递进关系：
约束条件：
这是一个非常扯淡的条件，但是在计算量较小时确实是一个有利的选项，尽快下采样以节省计算资源，作者倒是竟然在此后的所有实验都采用了这个约束条件。从结果来看，由此经得到的确实优于，但是后文中作者也实验得出当计算资源较为充足时，这一条件就不再是一个正确的选项了。

RegNet

Block宽度的拟合

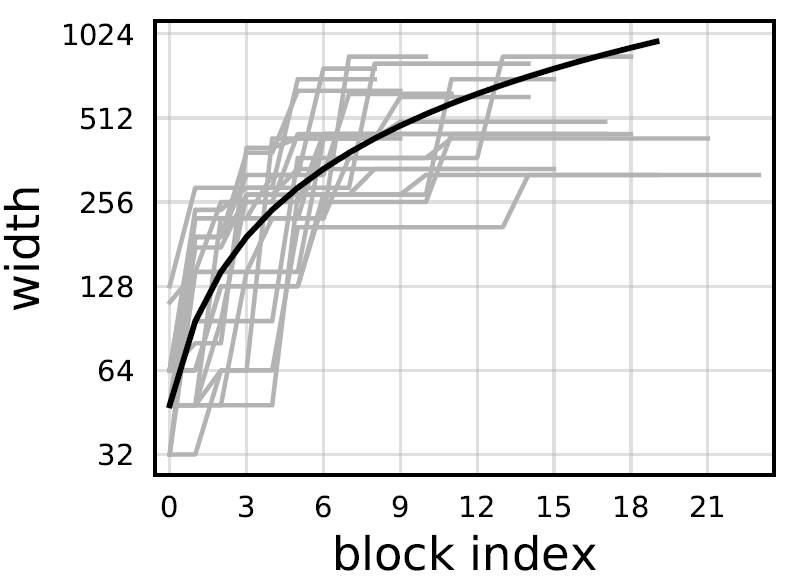
作者观察了性能最好的20个在计算量约束下的模型，提出了一种猜测：对于第个Block，其宽度有，如下图黑线所示。

约束条件：不同Block的宽度是线性递增的
但是这种约束会使得同一stage中每个Block的宽度不同，对此作者引入了一系列中间变量和超参用于量化。引入超参，记第一个Block的宽度为，宽度的增长率为，我们可以得出：

引入另一超参。我们计算每一层的宽度时，首先通过上式得出，再通过下式得出，对取整后得出量化后的，每个stage中所有Block宽度都相等的宽度


得出第个Block的宽度，而第个stage的Block数即为，通过取整后的来控制stage。此时约束条件可以变为：在超参的指导下，根据以上规则构建出的网络，并以此构建了构造空间。
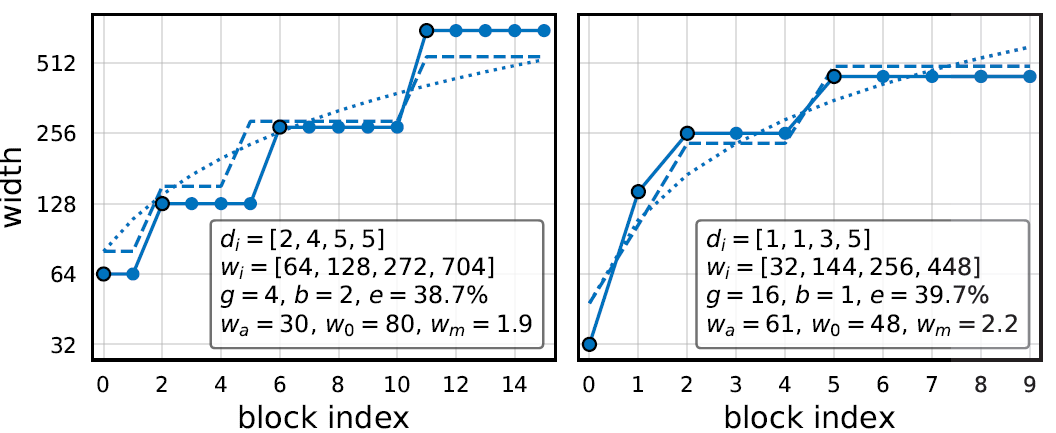
作者展示了中性能最好的两个模型，并将它们与该约束条件建立的宽度拟合进行了对比，两者基本吻合。

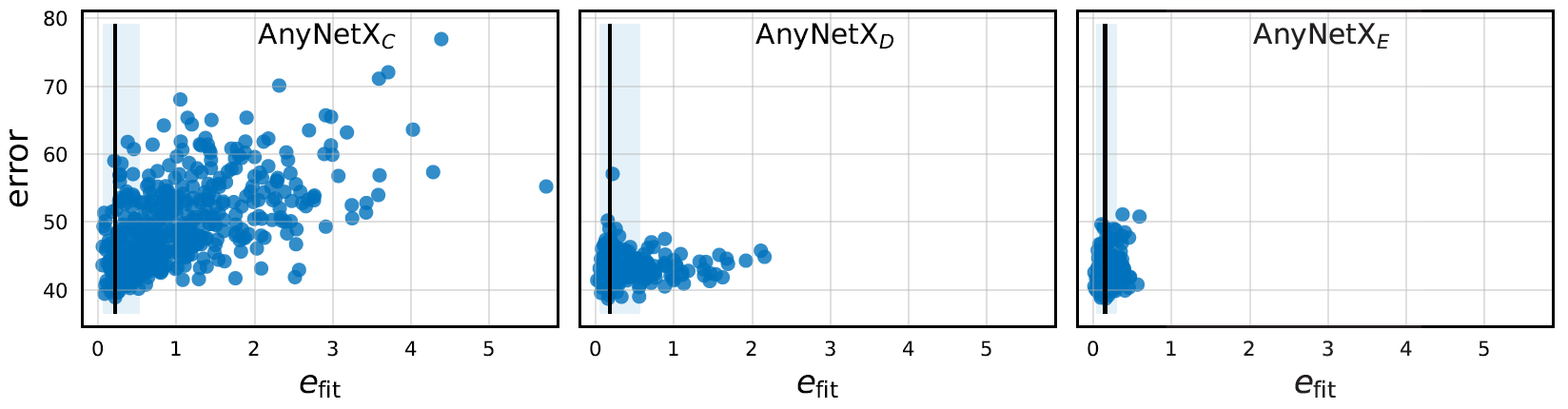
对于每一个随机采样得到的模型，我们都可以通过给定的，栅格搜索得到，并记录：

是一个衡量模型与该约束条件相符的程度，越小代表模型的结构越符合该约束。作者还作出了的散点图，可以发现随着从更新到的过程中逐渐变小。因此作者有理由猜测是影响模型性能的一个指标。

RegNet构造空间

在上述的Block宽度拟合（文中称为quantized linear）的制约下，我们构建了一个新的构建空间。由于每个stage的Block数现由控制，我们只需要控制网络的总深度即可；另外代表网络的初始宽度，代表虚拟的，网络中每个Block的宽度递增率，控制了每次下采样时宽度翻为多少倍。此时的构建空间为：、、以及缩放因子和分组卷积宽度。由于作者后来发现较优的往往随模型规模增大而变大，因此后续在不同计算量限制下搜索时，的构造空间随计算量限制有所调整。
有一个论文中没有提到的需要注意的是，网络深度的取值与是相关的，由于每个stage的Block数受控制，为保证网络不会在stage3结束以及不会进入stage5，有：

经过这么一系列构造空间浓缩，我们成功将空间大小从降到了（虽然这个644是怎么
来的令人迷惑）：

探究RegNet构造空间

由于RegNet提供的模型大多是质量较高的，因此作者在RegNet上采样时只采样较少的模型数，但是每个模型都训25epoch，SGD(momentum=0.9)，bs=128，lr=0.1余弦衰减，wd=5e-5。

超参的影响

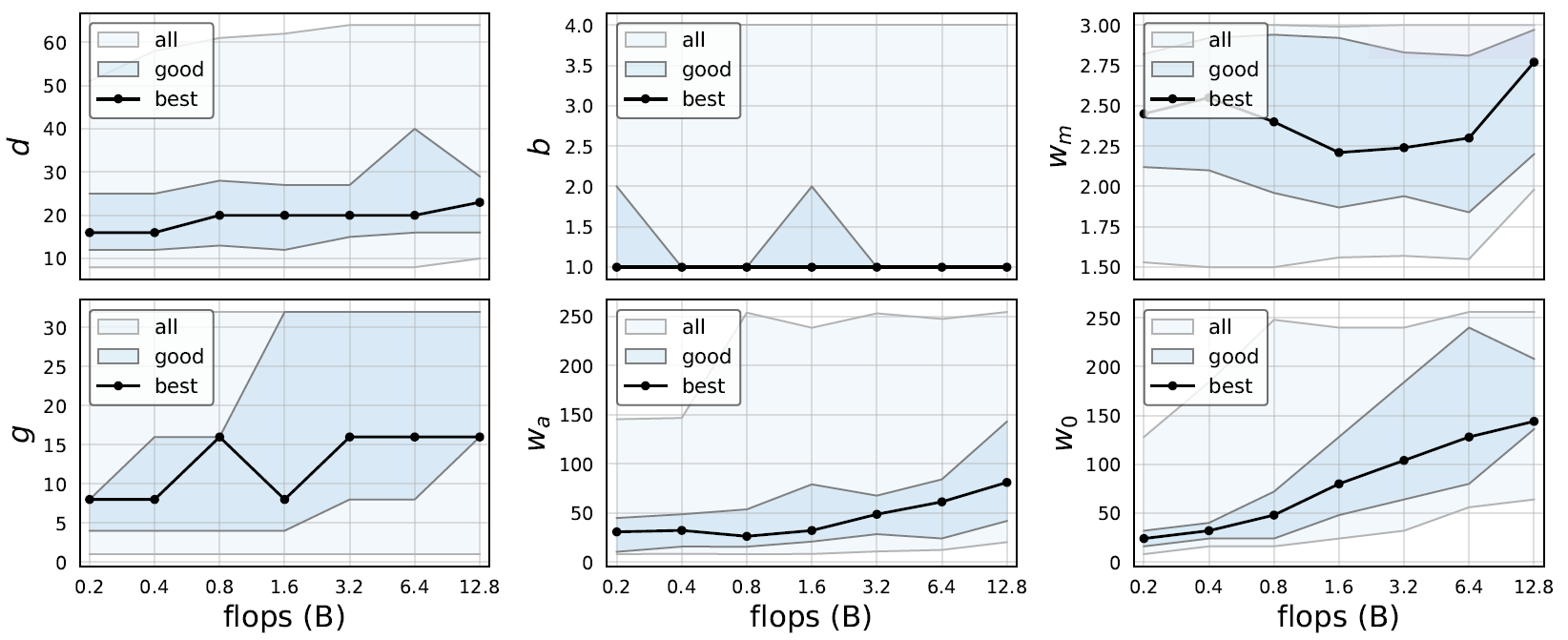
从图中可以发现，不论计算资源限制为多少，最佳的深度始终为左右（~60卷积层），这与ResNet通过加深网络以获得性能提升、EfficientNet的多尺度缩放有所不符。
不论计算资源限制为多少，表现好的网络总是偏向于选择，即不做通道缩放，这与ResNet Bottleneck、MobileNet v2 Inverted Bottleneck有所不符。（后续作者发现用普通卷积替代分组卷积时，确实更好）
最佳的下采样通道扩增倍率为左右，这与我们平时经常采用的也有所不同，毕竟平时我们只是希望各个Block计算量相等而没考虑效率最优化。
随着网络规模增大而逐渐变大。

开销分析

平时我们衡量网络开销的时候常用的指标为参数量、FLOPS等，作者提出了应该考虑激活值的数量（就是Tensor的总大小），显存访问的开销并不小于计算开销。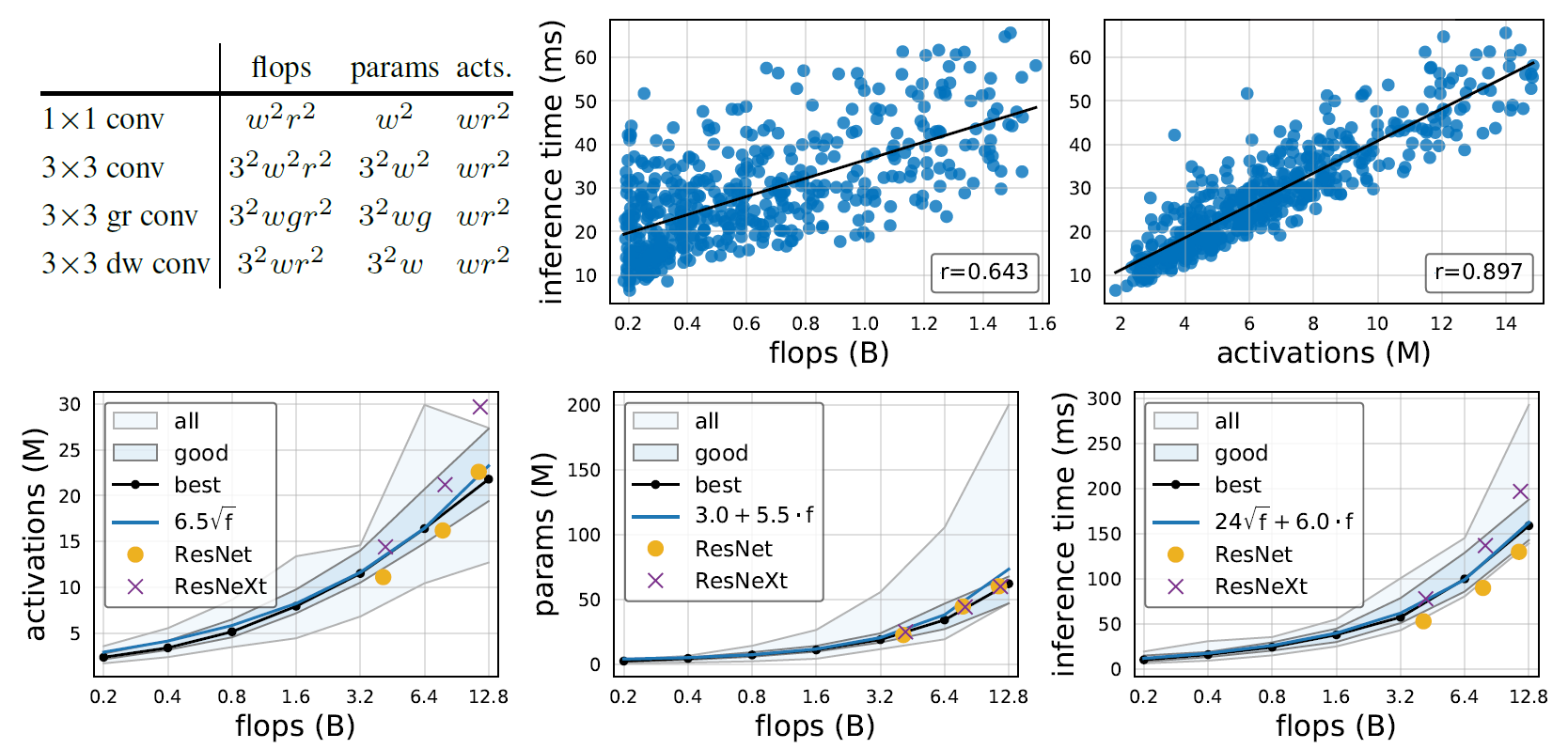

从上图可见，FLOPS与GPU推理延迟的相关系数为0.643，而激活数与GPU推理延迟的相关系数高达0.897。作者分析了空间中的sample，发现性能较好的模型大致均符合下述关系：

更多约束条件

将缩紧为了，并将缩紧为了，同时引入了上一节“开销分析”中的结果，在限制FLOPS的同时追加限制参数量、激活值。
由于：



则有：

激活值相对FLOPS不能过多过少，要求我们保持好的关系；而参数量不能过大（图中所示不好的模型基
本是参数量过大而非过小）单纯要求我们不要分配太多深层stage的Block，因为只与特征图分辨率有关。

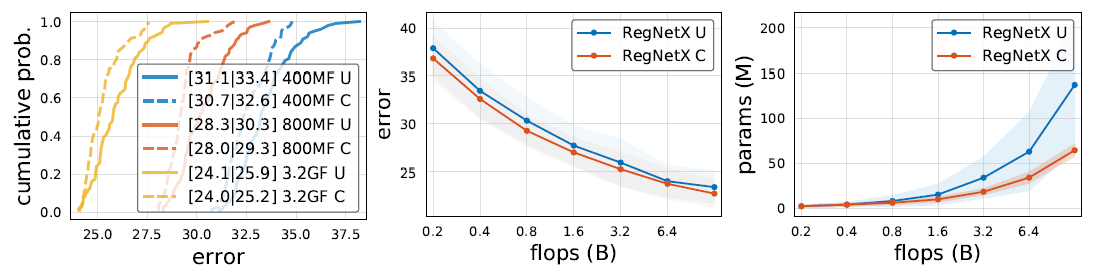
U代表的是原始构造空间，C代表的是加了上述额外约束的构造空间。可以看到不论在概率分布、最佳准确度、参数量方面，C空间均优于U空间。

鞭尸MobileNet v2和EfficientNet以及SE有效

作者尝试了MobileNet v2 Inverted Bottleneck采用的、DW卷积采用的、EfficientNet提出的输入分辨率也应一起scale-up，并对它们进行了鞭尸。

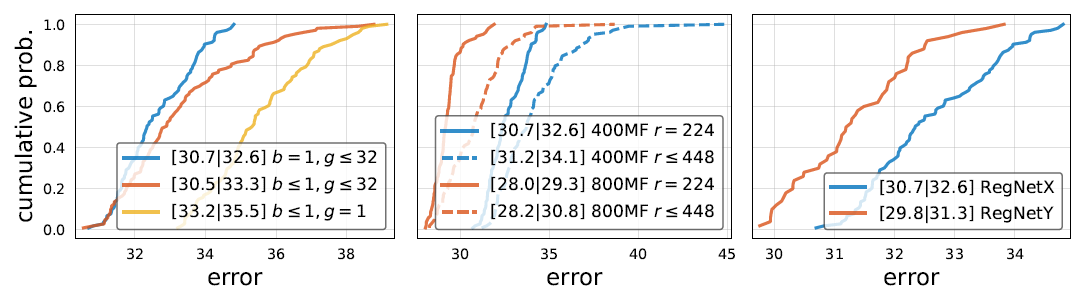
对于带来的副作用确实值得思考，但感觉也需要仔细分析一下是否增减约束会带来不同的结果。作者也尝试了在大计算量下下对性能的影响，也只会带来劣化。
但是改分辨率会劣化这个我还是存疑的，就算作者在400MF、800MF两个计算量下做了实验，但这两个计算量依然算非常小了，毕竟使用380作为输入分辨率的EfficientNet-B4都已经由4.2BF了。另外测的到底是还是作者也没有说清，如果是前者的话会劣化当然有可能了。
另外作者还验证了SE的有效性，将RegNetX Block中的3x3卷积后添加SE模块（r=0.25）得到RegNetY Block。
不过这也给了我一种启发，以前我一直对于“开销相等时，大网络中MobileNet的DW卷积是否会优于传统卷积”存疑，也可以用这篇论文的方法进行论证（就是有点费卡）。

搜出来的网络Family

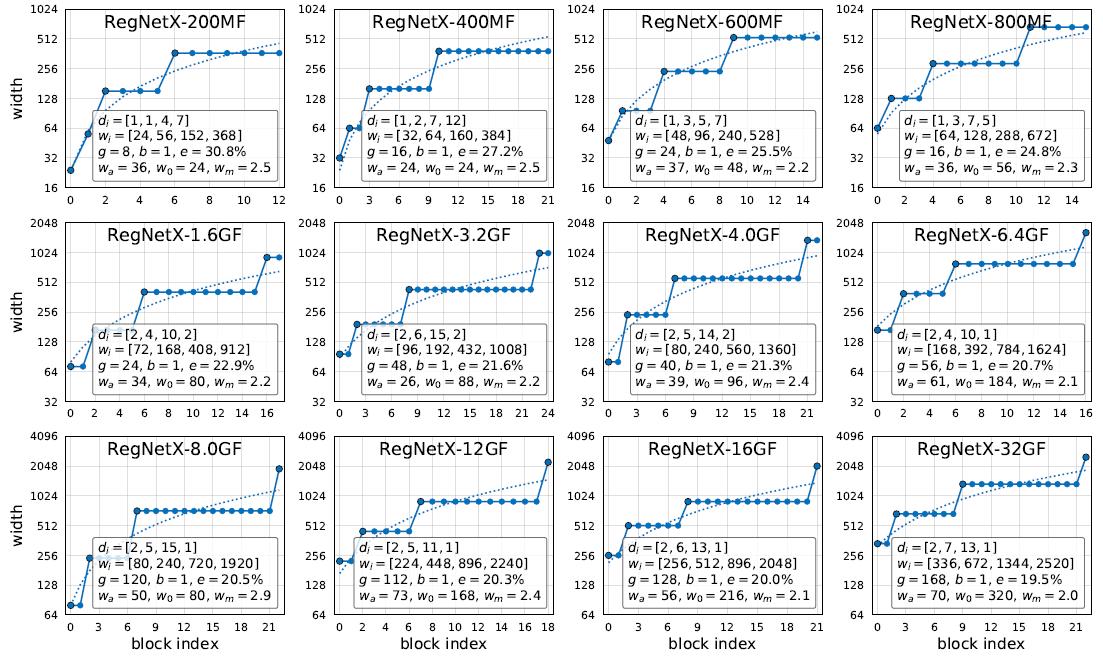
作者从中发现了：

1. 小模型stage4的Block多，大模型stage3的Block多。（这点之后在遗留问题的第5点里我提出了质疑）
2. 分组卷积宽度随着模型规模增大而逐渐变大。
3. 模型深度随着模型规模增大没有明显的变化。

实验结果

作者表示他没有使用任何其它乱七八糟的优化方法，譬如Cutout、DropPath、AutoAugment等等，也没有使用除了weight decay外的任何正则化手段，在只训练100epoch时就能实现非常好的结果，而MobileNet v2与EfficientNet等网络需要250epoch。但作者全程只比了大家都只训100epoch的结果，没给出RegNet训250epoch并加上优化方法的结果，就有点迷幻。


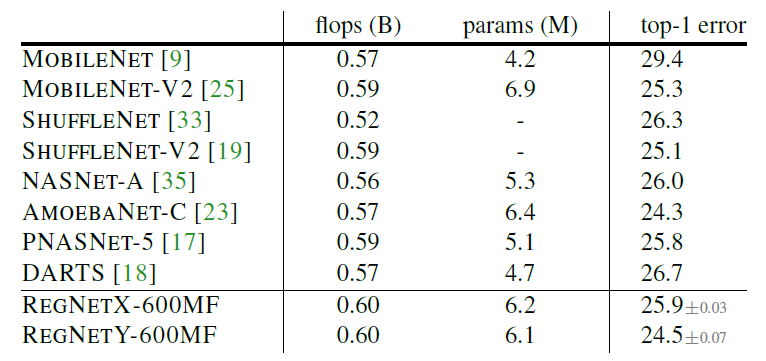
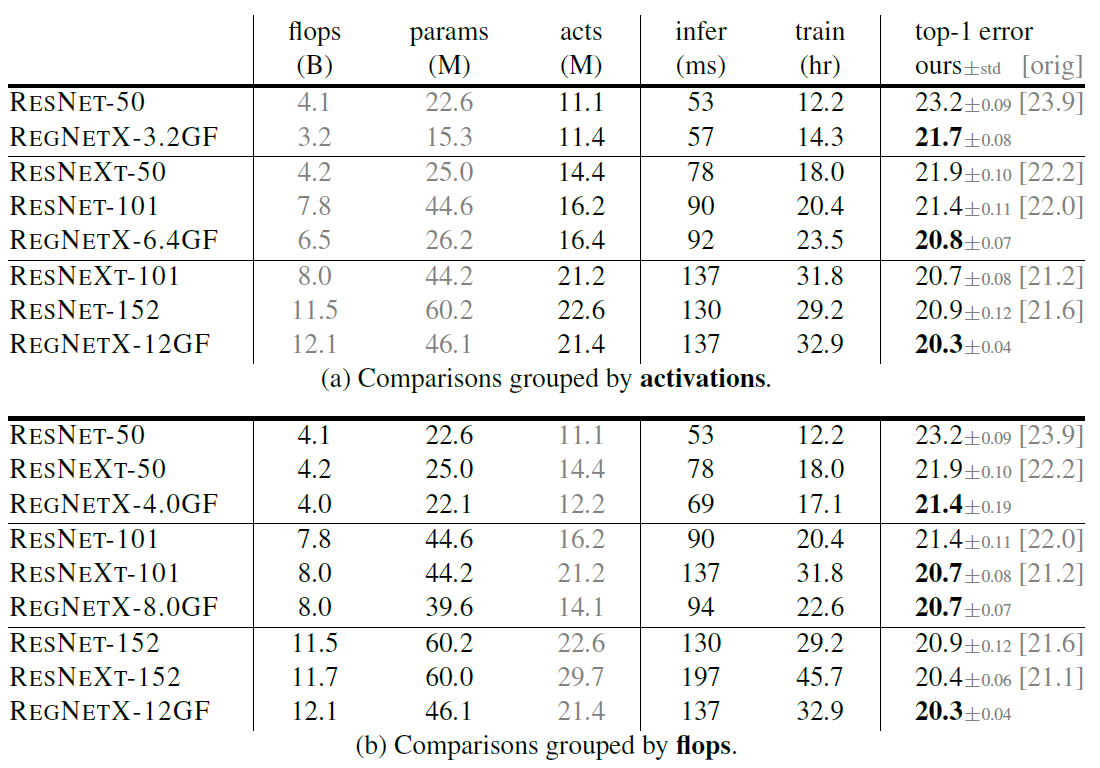
与EfficientNet的对比（两者都只训100epoch去除优化方法，EfficientNet原论文的结果在最右侧给出）：

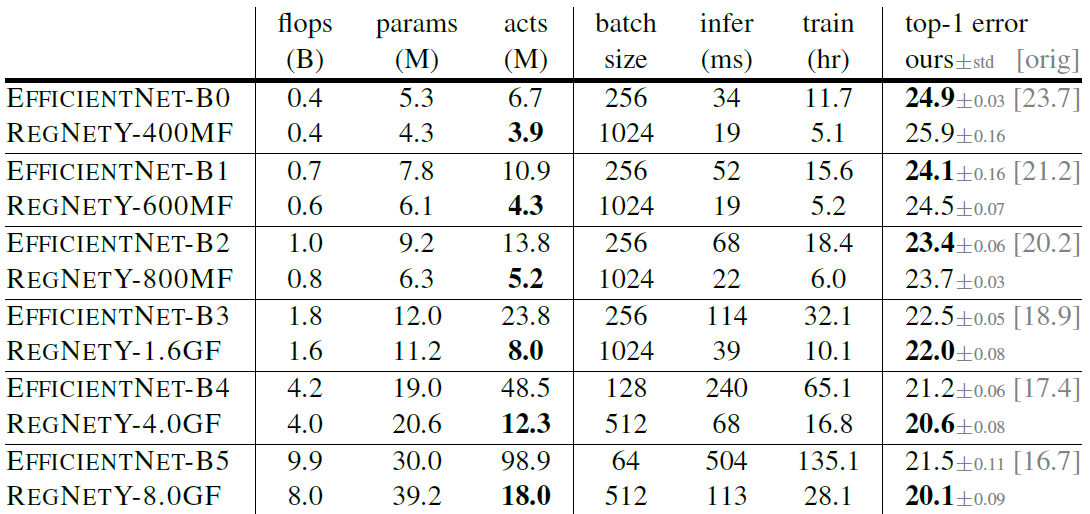
作者表示，由于EfficientNet全部用了DW卷积，其激活数（整个网络的Tensor大小只和）远大于RegNet，这
使得在GPU推理时RegNet远快于EfficientNet。这也就是开篇提到的，RegNet在同样性能下GPU推理速度比EfficientNet快了5倍的由来。

其它对比实验

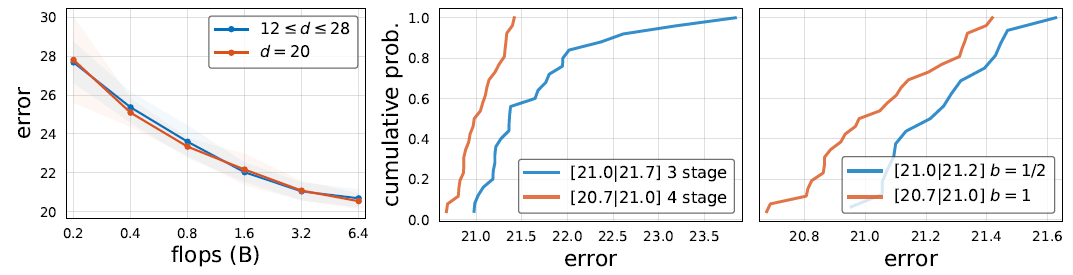
1. 作者比较了与固定的对比，发现两者在各个计算量限制下竟然均无明显差别
2. 由于大模型第4个stage的Block相当少，作者尝试了的大模型只有3个stage，结果炸了

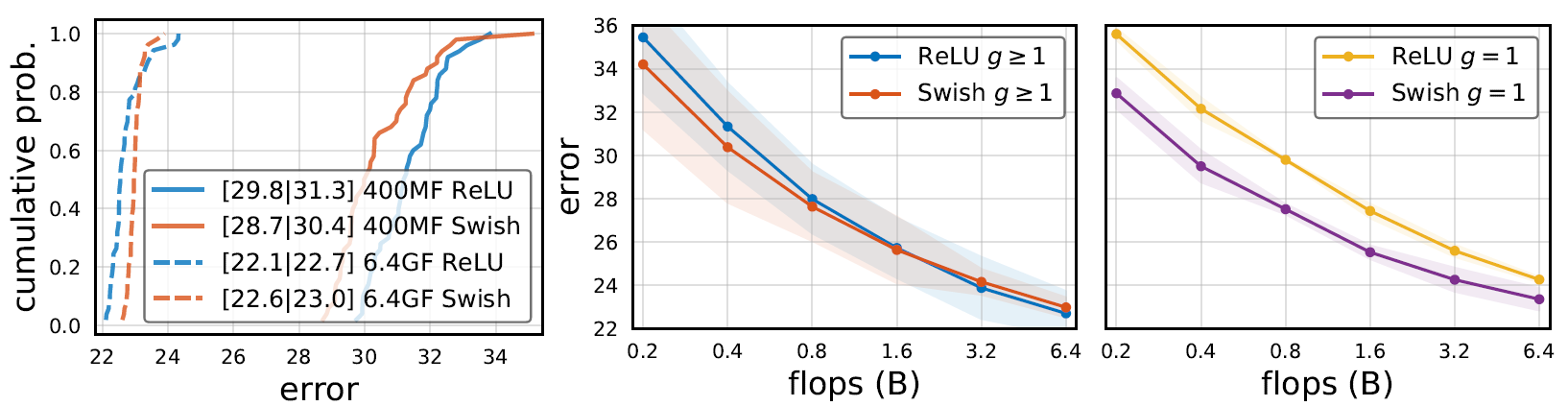
1. 作者尝试对比了Swish和ReLU，发现在小模型中Swish比ReLU更好，但大模型里ReLU更好。但如果限制采用DW卷积，那Swish会明显比ReLU好，这也正是为什么MobileNet v3采用了Swish但我改用Swish一点用都没。

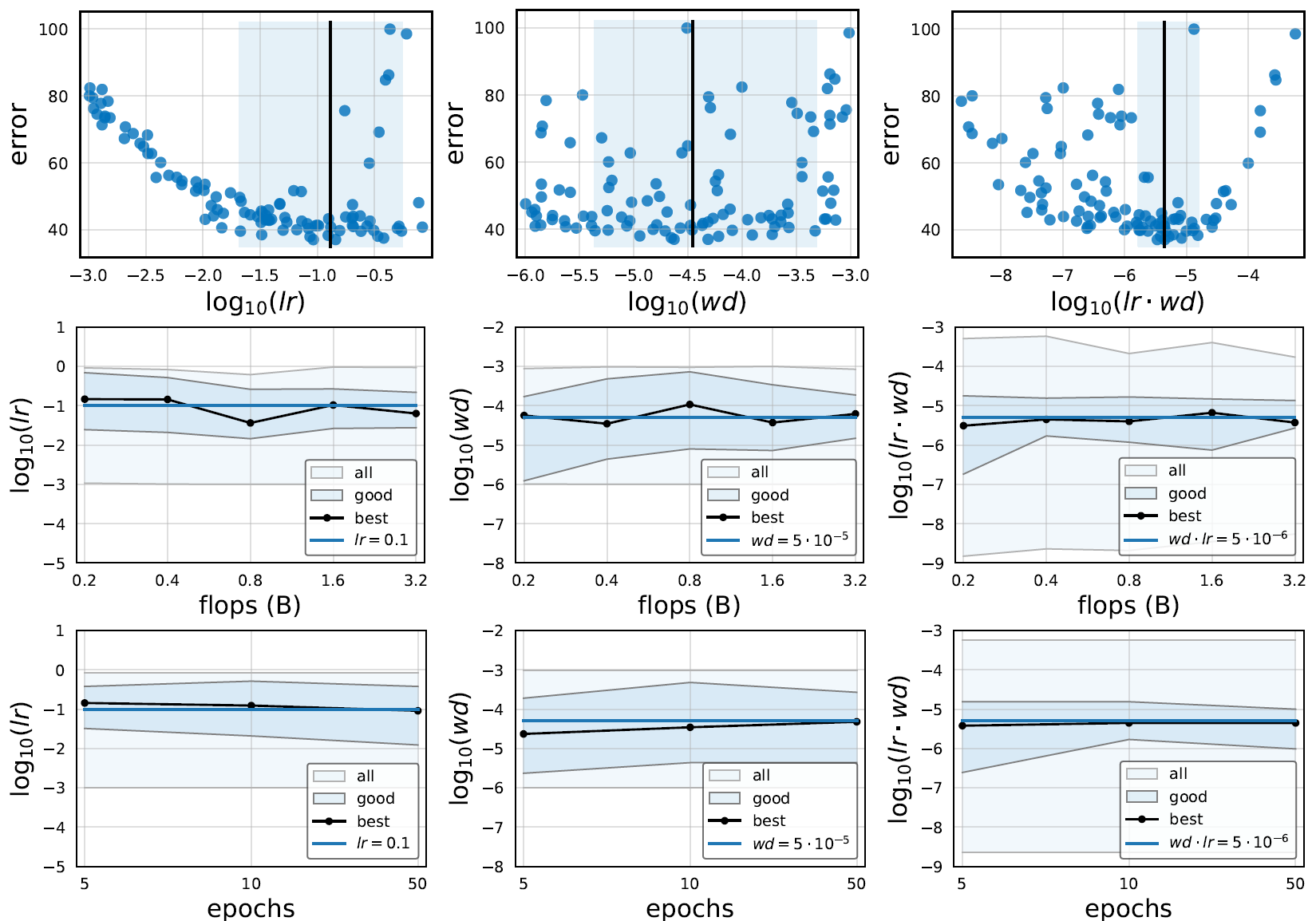
1. 作者研究了初始学习率、L2正则化系数的影响，实验中采用的是。

空间浓缩过程的总结

1. 所有stage共享通道收缩率与分组卷积宽度；
2. 更深的stage，其宽度与Block数都应大于更浅的stage，即；
3. 假设Block的宽度呈等差递增，不同stage的宽度呈等比递增，用模拟Block的stage数以控制stage。隐式地限制了stage1~3的Block数近似呈等比递增。
4. 约束、，模型参数与激活值大致符合、。隐式地约束了低FLOPS模型stage4的Block数偏多，高FLOPS模型stage4的Block数偏少（详见遗留问题5）。

遗留问题

1. Block宽度拟合过程中提出每个Block宽度呈等差递增，这个假设的约束是否太大了？
2. 通过控制stage带来了另一个隐式约束，就是stage1~3的Block数近似呈等比递增（因为是等差数列的对数），是否不合理？

提议：要让每个stage的宽度相等，直接指定中Block的宽度为的倍它不香么，模型多样性还更好。此时模型的构建空间超参包含。

1. 在RegNet构造空间上重新检测所有stage共用是否影响模型质量？
2. 作者说更好，在ResNeXt的基础上微调分支数、Block宽度就可以简单验证一下？
3. 作者发现大计算量模型更偏向于stage3的Block比较多，小计算量模型更偏向于在stage4的Block比较多。可是这不是废话么，在更多约束信息一节中作者已经限制了参数量与FLPOS的关系，并且又在Block宽度的拟合一节中限制每个stage的Block数基本呈等比递增，当然会这样了啊！在限制下，低FLPOS模型受到的制约较少因为有常数在，而高FLOPS模型受到了制约就大了，由于，只能通过减少stage4的Block数来满足作者提出的两个约束。因此不是只有best模型会这样，只要在这个约束下所有模型都会这样！
4. 利用决策树、蒙特卡洛搜索树，提供无监督或弱监督的空间浓缩方法。