SkipNet(ECCV2018)
论文:https://arxiv.org/pdf/1711.09485.pdf(强化学习)
创新点:结合了监督学习和强化学习
难点:决策模块不可导,如果使用gate的决策模块过sigmoid乘进残差并在推理时用hard截断效果很差(参考不finetune的量化),因此引入强化学习。
文中说到的reparametrization techniques其实就是把0/1决策问题转成softmax从而变得可导。
SkipNet的范式如下所示,其中为第
层的gate函数,其输出只有0/1离散值。(为啥过卷积时shortcut没了???)
gate函数不仅需要有足够的表征能力,又必须足够轻量(废话不然Block都算完了你才做完决策),文中给出了三个示例的gate网络(其中c网络的共享权重部分包括一个单层,宽度为10的LSTM和一个全连接)。开销方面,a相当于Block开销的19%,b相当于Block开销的12.5%,c相当于Block开销的0.04%,作者在后来的实验中表示,RNN的表现比FeedForward更好(毕竟能用到浅层的信息)。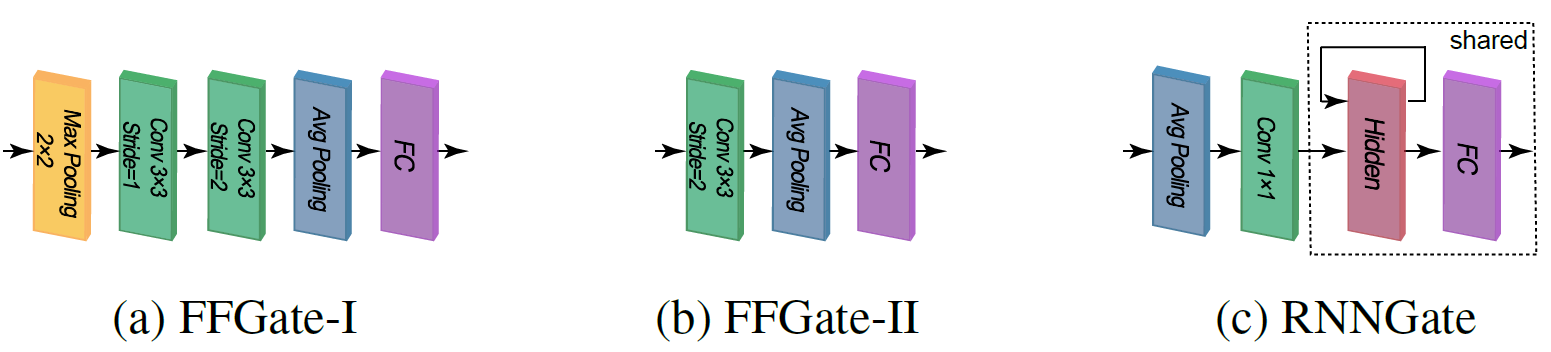
训练方法
文中提出的目标函数及其梯度:
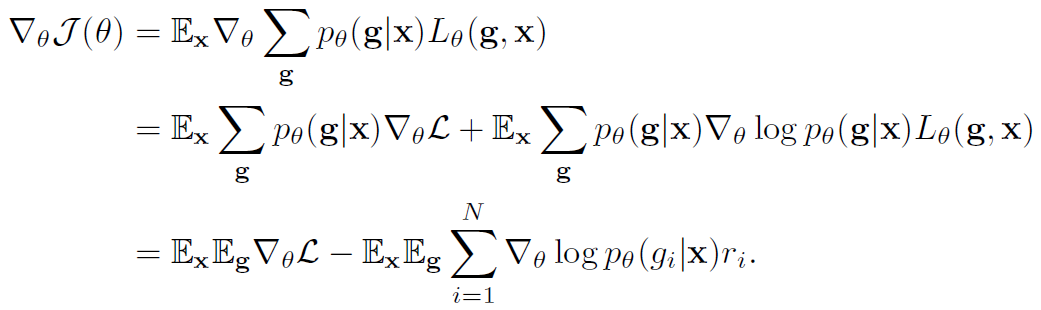
论文中说,直接训整个带gate的SkipNet的话效果很差,可能因为是由于强化学习捕获到了训练初期的低级特征限制了网络的表征能力。
因此论文中采用的方法是先正常做监督学习,gate模块通过softmax输出,前传时做0/1硬截断,反传时不截断;然后再通过强化学习finetune。
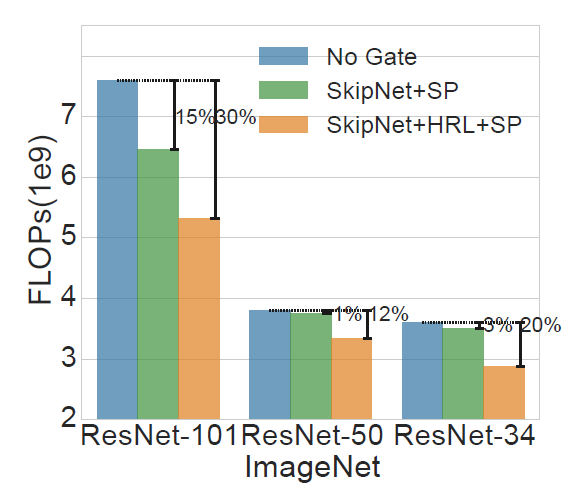
实验结果
开源实现
之前说了训练的时候前向用hard 0/1截断,反传用softmax,前传时0/1截断是依概率随机的而非看谁大于0.5就取谁!
LKAM(2017)
(Parsimonious Inference on Convolutional Neural Networks)
论文:https://arxiv.org/ftp/arxiv/papers/1701/1701.05221.pdf
说白了就是SkipNet的Supervised Pretrain部分,不过用在了channel粒度上而非用在layer粒度,且没用Hard门控而用了Soft门控,并且直接在推理阶段做硬截断,这种方法是SkipNet里说过效果极差的方法。另外由于做的实验奇奇怪怪,结果存疑,但思路可取。
BlockDrop(CVPR2018)
论文:https://arxiv.org/pdf/1711.08393.pdf
Policy网络
作者直接是在预训练的ResNet上动手的,这个SkipNet做了带门控的SP不一样。实测如果SkipNet直接在预训练的ResNet上做HRL效果很差,模型不耐裁且HRL的训练过程极不稳定。BlockDrop的实验没做所以不确定。
另外不同于SkipNet用了LSTM融合Block间的序列信息,这篇论文的Policy网络是直接基于输入图像的,用到了一个ResNet8网络(ImageNet backbone的话是ResNet10),直接在全连接层生成所有Block的Gate Policy。譬如backbone是一个包含27个Block的ResNet56,那么Policy ResNet8的全连接层输出就有27维,分别对应了backbone的每个Block Gate。
作者说这种single-policy的方法比sequantial-policy的方法效率高,后面还做了实验论证(同样准确度、使用同样的Block数),虽然没有公开这一部分的实验细节。我是觉得有点神奇,SkipNet的门控部分用了LSTM,每个门控的开销都极小效果也不错。作者的实验直接说sequantial-policy的额外开销过大,做条件计算还不如跑full backbone。
训练方法
不同于SkipNet的HRL,作者先冻结了backbone单独训Policy Network,然后再进行联合finetune。
os:其实我有点费解,原始backbone都是不耐裁的,就算用强化学习决策丢Block应该也会炸。我做SkipNet实验的时候,对原始baseline裁的时候由于模型不耐裁,Policy会在一个epoch内对所有Gate输出1,就算给偏置也没用,不知道这篇论文的方法怎么样。
Reward的计算
训Policy Network时,Reward的计算方法:
os:其实这我也有点费解,应该full backbone预测正确而条件计算的子网络预测错误,裁应该给负的reward
吧。另外这里是个超参,郑老师说复现的时候很难调。
Reward归一化
另外为了避免Reward在训练过程中的巨大方差,作者对Reward做了归一化,这个学强化学习的时候李宏毅也说了,应该给Reward一个合适的先验偏置使得其期望接近0。作者提出的方法是对每个input都根据当前的Policy找出可能性最高的一条路径(即每个Gate都取可能性更高的那个决策),计算平均Reward作为偏置。我个人觉得这个方法过于麻烦,直接用指数平滑平均维护这个偏置就能取得很好的效果。
Policy概率钳位
为了鼓励模型探索新的路径,防止模型一直采用某一个Block或者直接打死一个Block,作者对Policy Network输出的每个Gate的0/1概率分布进行了钳位:
以此将固定在
范围中,论文中取了
。可是我做SkipNet实验的时候这么做没用,它该舔的Block还是舔,该拍死的Block还是无情地一巴掌拍死,贼J2任性我都不知道说它什么好。
Curriculum learning
总而言之就是让模型从简单的开始学,比如一开始一次性学27个门控比较困难,就第一个epoch只学最后一个门控(前26个Block全部开启),第二个epoch学最后两个门控,直到第27epoch开始放开所有门控的训练。作者提出这么做会使得Policy Network的训练比较有效。
训练过程总览

实验结果
图中K代表使用的平均Block数,Acc是联合finetune前(只单独训Policy Network)的准确度,Acc(ft)是联合finetune后的最终结果。
Channel Gating(NIPS2019)
论文:https://arxiv.org/pdf/1805.12549v1.pdf(混合精度)
这篇论文的作者和Precision Gating是同个作者,两篇论文的思路也惊人的相似,只不过PG混合精度是通过不同bit数的量化实现的,而这篇论文是取少量输入通道计算输出作为低精度结果(譬如64个输入通道只取8个,先算出64个输出通道的结果,再判断哪些pixel需要通过剩下56个输入通道计算高精度结果 )
基本思路
虽然平时我们说,pixel-wise地裁input没有任何作用(不过pixel-wise地裁output可以),但整个通道裁input是可以起到加速效果的。
作者将权重层的拆分为了
%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-79%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22775%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1831%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-57%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-70%22%20x%3D%221335%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2217%22%20x%3D%223454%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(4177%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-70%22%20x%3D%22809%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%225427%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(6428%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-57%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%221335%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2217%22%20x%3D%228014%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(8737%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%22809%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=y%3DWp%2Ax_p%2BW_r%2Ax_r&height=20&id=T664g),其中
为大小的张量,
为大小的张量;对应的为
,
为
大小的张量。
作为低精度结果,被用于输入门控
预测是否需要计算高精度残差
(下标p代表predict,下标r代表residual)。
其中是一个介于0~1间的超参。作者对不同
的效果进行了研究,发现1/8最佳。
另外在的划分上,作者直接单纯将排序靠前的幸运通道作为
而剩下的作为
。作者带了一句说如
果做group、shuffle等能在ImageNet上提一个点。
门控采用了熟悉的Sigmoid+STE配方:,其中
控制门控函数
的平滑程度,作者对不同研究得出
最好。

另外作者提出,在过gate之前也过了一个恒定的BN(见计算图中的BN1,这个我相当相当费
解)。另外有些pixel是通过获得结果的,另些则通过
得出结果,此时输出的入度不同,数据分布也必然不同,直接对最终的输出做BN必然不合理。
该权重层的计算图:(其中后没有点积,应该直接加,图画错了)

约束条件
虽然我们通过来裁,但如何在目标函数中引入约束来鼓励网络裁
的计算,作者展开了讨论。
- 选择
的目标值
,将
加入目标函数;
- 将
的均值加入目标函数(与SkipNet相同);
- 直接锁死
。
作者做了实验发现(1)是最好的方法,最直观的(2)竟然还是最差的方法,如下图左所示。作者分析了为什么会有这样的结果,发现采用(2)方法模型总会很任性地打死某些layer或舔某些layer,让某些layer全过低精度通道或全过高精度通道(这不是和SkipNet的问题一毛一样吗!)
实验结果

SeerNet(CVPR2019)
论文:https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8954289&tag=1(混合精度)
SeerNet的思路其实很简单,可以用一句话概括:利用ReLU会将负数变0的特性,用低比特量化跑一次前向Q-Conv后,记录结果为负的点,并在全精度前向S-Conv时不计算这些点而用0填充。这是一篇可以算条件计算(决策模块是低bit的原始网络),也可以算混合精度量化(如果S-Conv用不用fp32而用高bit量化)的论文。
如果Q-Conv对于输出符号的判断结果准确那会是一种无损压缩手段。(对于vgg16这样的有maxpool层的网络,通过Q-Conv预测每个block的最大值,并在S-Conv时忽略其它pixel)
稀疏率
这种裁剪方式依赖于output的稀疏率,也就是ReLU后为0的pixel的比例。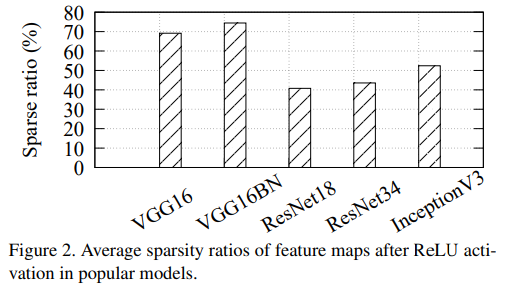

可以看出vgg16这种网络的冗余度很高,而ResNet18和ResNet34的稀疏率就低了很多(MobileNet v2应该更低)。
Q-Conv位数
由于只是用于预测output的符号,因此Q-Conv并不需要很高的量化位数,作者做了实验发现4bit就够了。作者是在CPU上做的实验,想不通为什么不用8bit,作者的说法是“For efficient storage, we use 4-bit format to cache our intermediate results.”。
实验结果



不同网络各层的开销分布与加速比: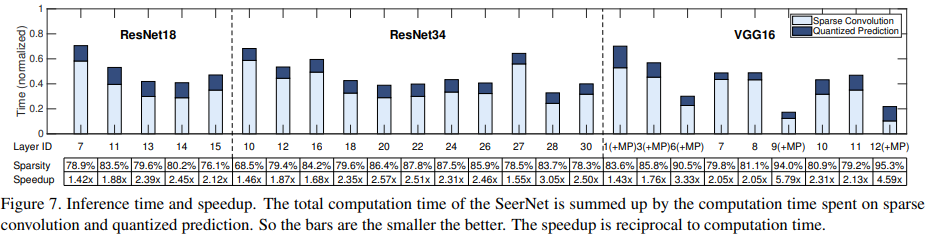
另外作者在vgg16上测了各层的,Q-Conv错预测的比例:
思考
不过不要生硬地将4bit量化的0~7标记为需要进行S-Conv的pixel,留一定的余量譬如将-1~7标记为正例是否会改善结果?
Precision Gating(ICLR2020)
论文:https://arxiv.org/pdf/2002.07136v1.pdf(混合精度)
其实这篇论文是SeerNet的改进版,论文中也详细介绍了SeerNet的思路并与SeerNet进行了对比。为了简单表达,将SeerNet的Q-Conv部分称为低精度网络,S-Conv部分称为高精度网路。这篇PG与SeerNet的主要区别在:
- SeerNet跑完低精度网络用于预测需要跑高精度网络的mask后丢弃低精度结果后计算高精度结果,而PG(论文里没说,开源代码里权重始终保持int8)在计算完低精度(比如3A8W量化)结果用于预测需要跑高精度的mask后,高精度结果(比如5A8W量化)是将残差加在低精度结果上的,而非丢弃低精度结果。
- SeerNet固定了0作为是否需要做高精度运算的阈值(因为ReLU会清零所有0以下的值),而PG主要预测哪些位置的值比较大比较重要,需要高精度结果(同时也隐式地预测输出是否会被ReLU截断),所以SeerNet只能用在使用ReLU的激活函数,PG适用性更强。PG将阈值作为了一个可训练参数(SeerNet的思考我也提出了阈值处理的问题,但没想到作为parameter)。
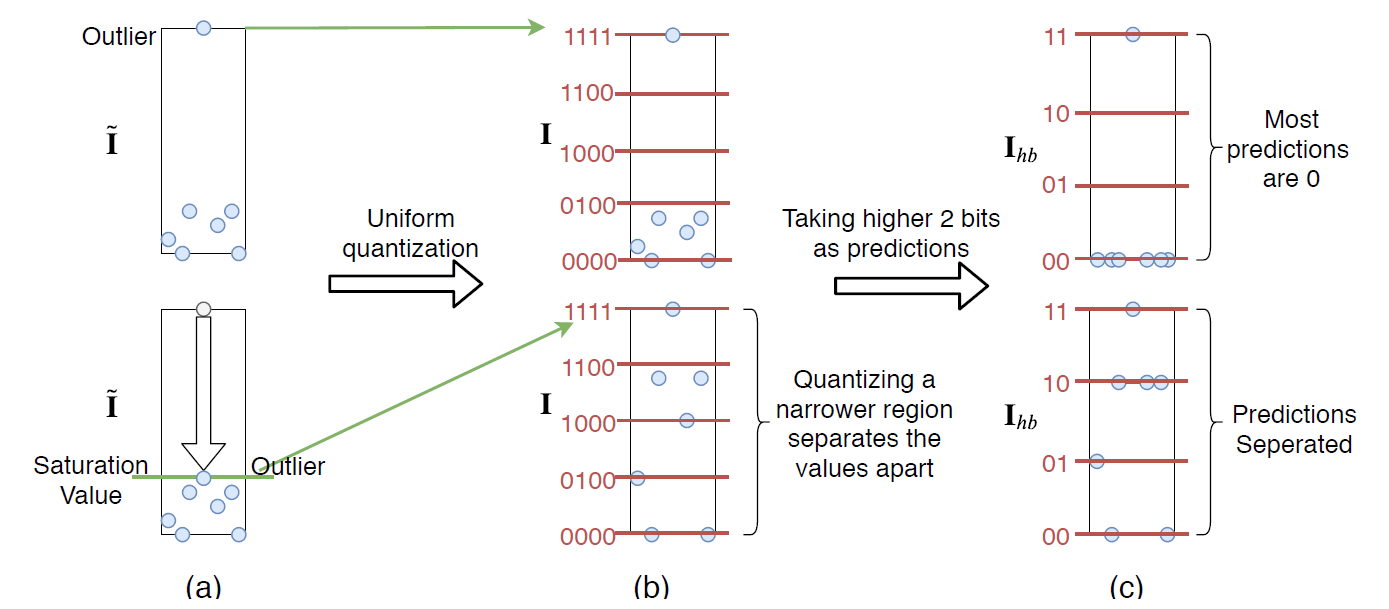
基本思路
PG针对的是纯int的特征图(input),不针对fp32的网络。一个位宽度的int型数据可以直接按高低位拆分为高
位和低
位(其中
):
比如
在保证权重为全精度int8时,权重层的输出可以表示为如下所示:
其中相对而言,是主导
的,我们可以通过
预测输出
中哪些位置将会被ReLU截断、哪些位置的比
较大比较重要。(其中为门控的阈值,为可训练参数,每层的每个输出通道都有自己的
)
(对比SeerNet的计算公式):
门控还是熟悉的Sigmoid+STE配方:,其中
控制门控函数的平滑程度,论文中取
。很神奇的是作者更早的论文Channel Gating(这篇博文里之前有提到)研究了不同
对结果的影响,得出
最好,更大的
会掉点,这篇论文却给了这么大的
。可能方法不同适合的
也不同吧= =
损失函数
其中为惩罚因子,
为目标阈值,我们可以通过调整这两个超参来满足不同要求。较小的
使得网络保留
更高精度,较大的则迫使网络节省更多计算开销。(加这个L2项强行限制
位于
附近总觉得有一丢丢蠢不过也想不到什么更好的办法了)
PACT离群值截断
由于ReLU激活函数没有上界,有些特征图量化后可能存在离群点(虽然基于直方图统计信息、KL散度等、最小化L2损失等可以缓解),作者引入了PACT,即对权重层的输出进行clip后再进行量化。其中clip的上界和下界
为可训练参数:
然后都直接训就行。
实验结果
CIFAR10结果:(UQ代表常规的线性量化,PACT为上下界截断后的量化)
可见恒定阈值的表现非常差,因此SeerNet的方法在低bit条件下估计肯定行不通的。另外我真的人傻了,ResNet20的3/2bit竟然比basline的4bit还好。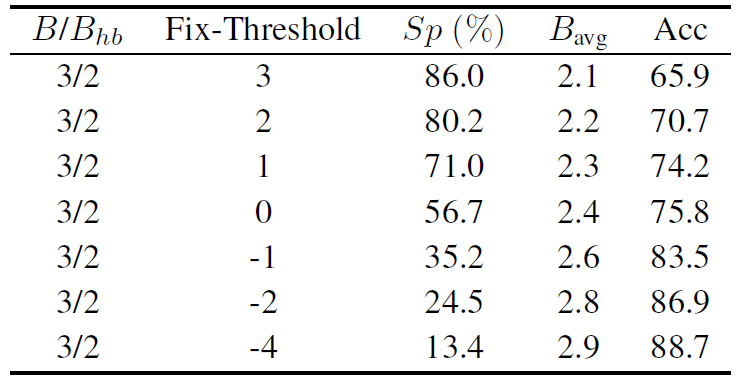
另外在恒定阈值时,即使把阈值设置为-4这么小到变态的值,依然相比动态阈值(91.2%准确率与90.1%稀疏
度)差很多,同时动态阈值的平均稀疏度又比恒定阈值为3高,就非常的令人费解……可能得做实验看看动态阈值训出来的阈值分布情况。
实验结果的解释
这里引用小铭的实验结果= =
实际做出来发现Fix-Threshold的准确度远远比作者给出的要高,后来发现是作者在做Baseline和PG的时候用了PACT,而在做Fix-Threshold的时候为了突出可训练效果好,在做Fix-Threshold当场把PACT关了……
超参
开源代码:https://github.com/cornell-zhang/dnn-gating
代码的config中,-w 8,-a 3,-pb 2,分别代表权重为8bit量化,,
(
)
论文中取超参,
。
另外一开始我还以为是fp32模型量化后做QAT的,结果开源代码里是从头训的……
ConvNet-AIG(ECCV2018)
论文:https://arxiv.org/pdf/1711.11503v3.pdf
这篇其实和SkipNet还是有点像的,最大区别在于loss的不同,以及ConvNet-AIG是为每个Block分配独立的feed forward gating网络而非采用LSTM。
ConvNet-AIG基本结构
论文提出,要让门控网络有效需要解决以下问题:
- 为了避免防止模式崩溃为不依赖输入特性的平凡解决方案(说人话就是一天到晚打死或者打通一个Block),作者将门控输出加噪声进行决策。作者认为门控的随机性至关重要。(就是训练过程不能直接谁大于0.5就决策0/1,引入了后面讲到的Gumbel分布noise)
- 使用了Gumbel-Max trick以及其softmax近似,使得离散的argmax决策过程可导。
- 使用计算量非常小的门控网络(avgpool+FC+ReLU+FC)
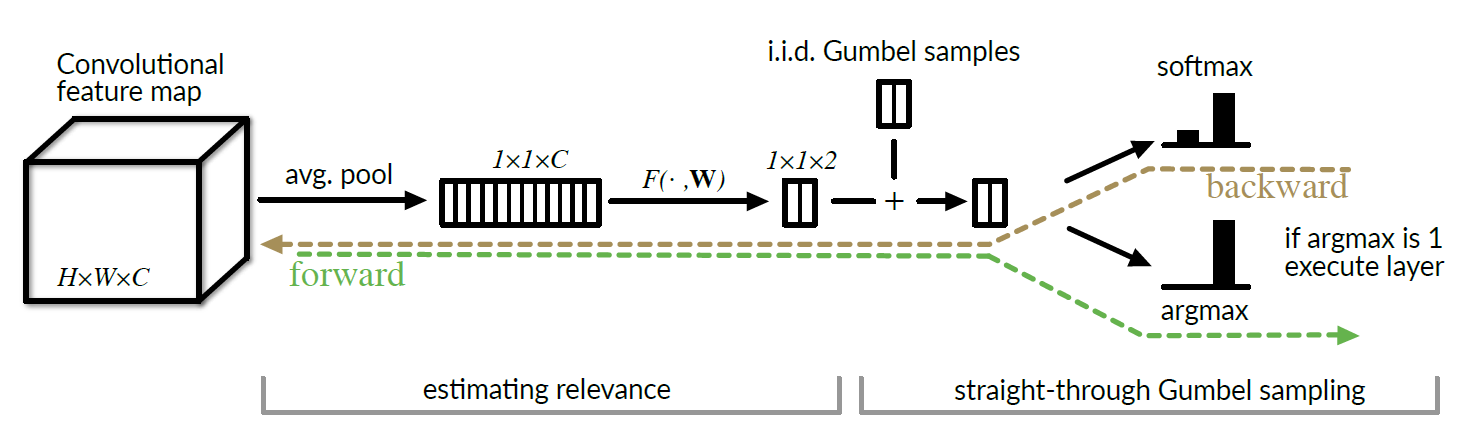
Greedy Gumble Sampling
最简单粗暴的采样方法就是谁大于0.5取谁(因为文中每个门控都是正/反二分类决策而非只有一个输出维度),会更容易导致模式崩溃,因为在抽样的时候没有考虑到置信度,并且这么做还是不可导的。
Gumbel Sampling的定义:对于给定的维概率向量
,我们通过以下方式进行抽样:
其中。
抽样得到的,是Gumbel分布的精髓所在。
但由于是不可导的,可以用softmax进行近似,得到近似的抽样样本。需要注意的是抽样得到的
是一个向量(但它是一个样本而非分布,需要理解这一点)。argmax得到的样本也可以看作是一个one-hot向量。
使用的时候可以在训练阶段用Gumbel-softmax而在推理阶段用Gumbel-max,也可以在训练阶段使用Gumbel-max但是将Gumbel-softmax作为STE。作者发现后者表现更好。
loss的构建
这个loss的构建着实是有那么点儿迷惑。作者直接在交叉熵上加了个正则化约束项以约束所有门控的开启率:(其实就是“Loss设计技巧”里讲到的Lb)
总loss则有:
实验结果

还是熟悉的训得比我ResNet56都低的baseline……ConvNet-AIG 110指的是在推理阶段开启所有Block的网络。文中还说到,ConvNet-AIG学会辨别层的重要与否,对于down-sample层会选择一直执行。(但这与我的实验结果相违背,down-sample层被一直执行代表adaptive还是没有做的很好)
但这篇论文睁着眼说瞎话啊!又说自己follow原始resnet v1的schedule又用了5e-4的weight_decay,还是用bs256、lr0.1训了350epc…以及标自己的结果用了最佳值,标baseline的结果用均值我也是……
**实测:用文中的schedule训(bs256、350epc)baseline能到95.13,ConvNet-AIG 110能到94.05,开放所有层后ConvNet-AIG 110能到94.31。并且效果对lossfact和temperature不敏感。**
好一个学术造假!

作者还记录了ImageNet上不同类别(大类)的图像在推理过程中使用的Block的分布情况:(这个实验还蛮有意思的)
FBS(ICLR2019)
论文:https://arxiv.org/pdf/1810.05331v2.pdf(通道级粒度条件计算)
这篇论文直接从BN层的γ入手,稀疏化BN的γ来实现通道级条件计算。
FBS基本结构
FBS的思路可以用一个公式表示:
↓
是基于上一层输出的特征图进行门控的决策结果。其中
是门控函数,简单粗暴的全局平均池化+单层FC+ReLU(这个ReLU不知道加它干嘛)。
是k-winner-takes-all函数,把向量中除了最大的k个值之外其他所有值都置零,不难发现
为动态裁剪中剩余通道的比例。
作者对的输出加了L1正则化(LASSO),并取
:
实验结果
烂,没有参考价值
GaterNet(CVPR2019)
论文:https://arxiv.org/pdf/1811.11205.pdf(通道级粒度条件计算)
相比SkipNet、BlockDrop这种以Residual Block为粒度进行skip的条件计算,这篇论文是以通道为粒度的。与
BlockDrop类似地采用了额外的Policy网络(文中称为GaterNet)来进行门控,但不同的是BlockDrop用了强化学习而这篇论文用了Improved SemHash来使得决策过程可导从而直接训练。
GaterNet基本结构
门控网络GaterNet由下式所示:
其中为特征提取器,论文中由ResNet20构成,
输出一个
维的特征向量送入
,
接收
维的输入并输出
维度的门控结果,其中
为整个backbone的通道数量(门控只对BasicBlock的conv2层,以及Bottleneck的conv3层起作用,其它卷积层执行完整计算),譬如对于ResNet56([9,9,9]):
当backbone比较大时,的参数量会非常大。文中应用了一个Bottleneck结构用于解决这个问题,先对
维向量降维至再输出
维的结果,参数量可从
下降为
。
论文中CIFAR数据集b=8,ImageNet BasicBlock b=256,ImageNet Bottleneck b=1024。
训练方法
论文中是把Backbone和GaterNet分别在分类任务上预训练,然后丢掉GaterNet的FC层并加上再开始联合训练。对于如何把GaterNet的输出变为真正的门控,论文用到了Improved SemHash,我没看过这个的论文不过看起来还是有点迷惑巴啦啦的。
记GaterNet的输出为,
为符合标准正态分布的噪声,首先相加得到
(噪声起到类似正则化的效果?)
而后分别计算得到两个门控结果,其中:
(相当于截平了sigmoid的最大最小部分)
以上相当于软门控,而
相当于硬门控。论文中的迷惑行为是随机抽取一半的
,另一半则是
。其中
不可导,
不存在,通过
进行梯度近似(还是有点像SkipNet的SP部分的,只不过这个sigmoid函数被鬼畜了一下)。
被启用的时候直接乘进计算结果就行,而
被启动时相当于硬门控,当然推理的时候时全部用
的,并且直接用
进行计算而非加噪后的
。
再BackBone和GaterNet预训练完后就可以开始联合训练了,loss里加一项的L1正则化用于稀疏约束。另外论文中只字没提该方法对于推理的提速和计算开销节省,加这个L1正则化好像也没啥用= =
实验结果
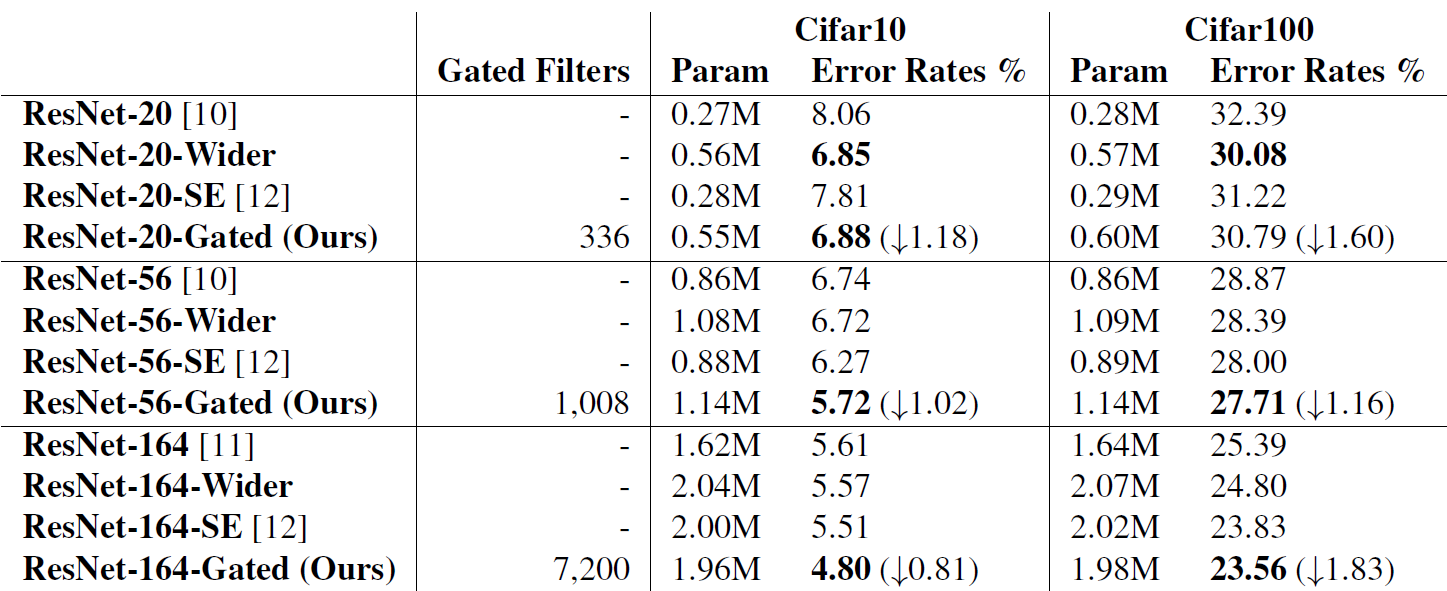
我不得不吐槽这个baseline真是烂的够够的了,我baseline训到72.96它加了优化才72.29。应该是用了原版ResNet v1论文中的1e-4的L2以及只训64k步(约164epoch)所以点这么低。
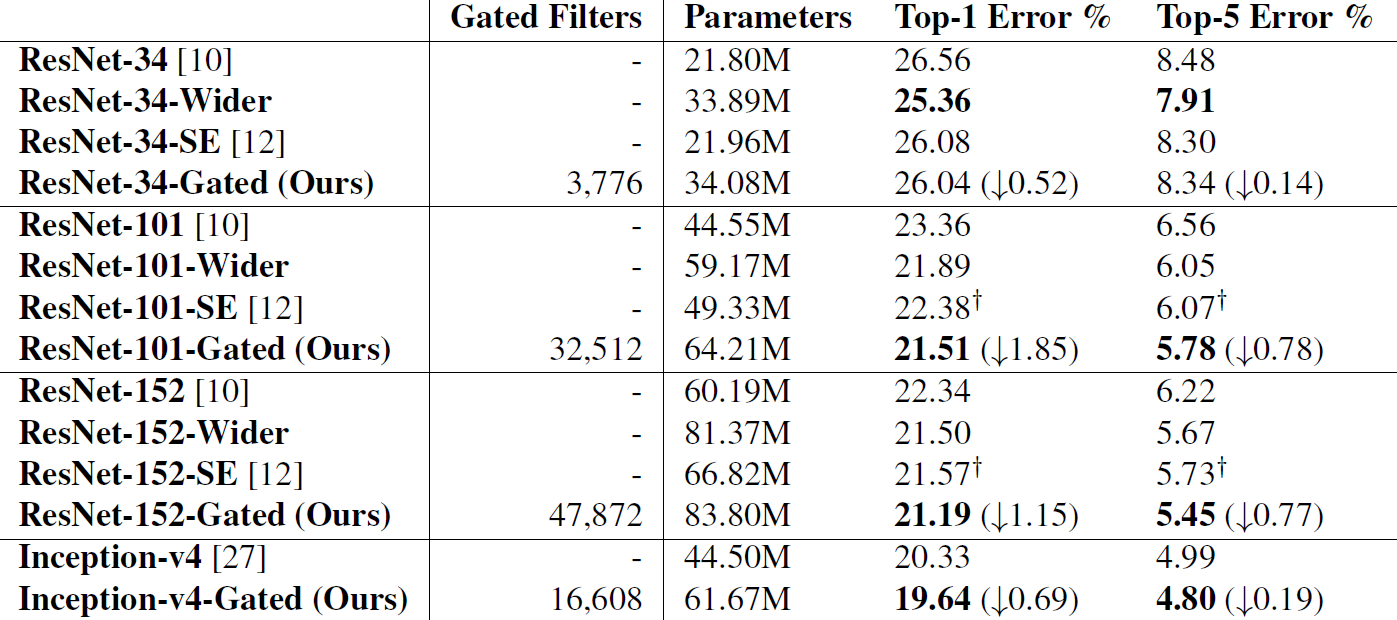
↓↓↓↓↓以下这些分布统计与数据统计的实验我觉得还是很有意思的:
论文还针对ResNet164(Bottleneck版ResNet110,但3个stage宽度为[4,32,64]而非[16,32,64])研究了各个gating在Test set上的开闭情况(感觉能训成这样而不是基本都是全开全必的很难得哎):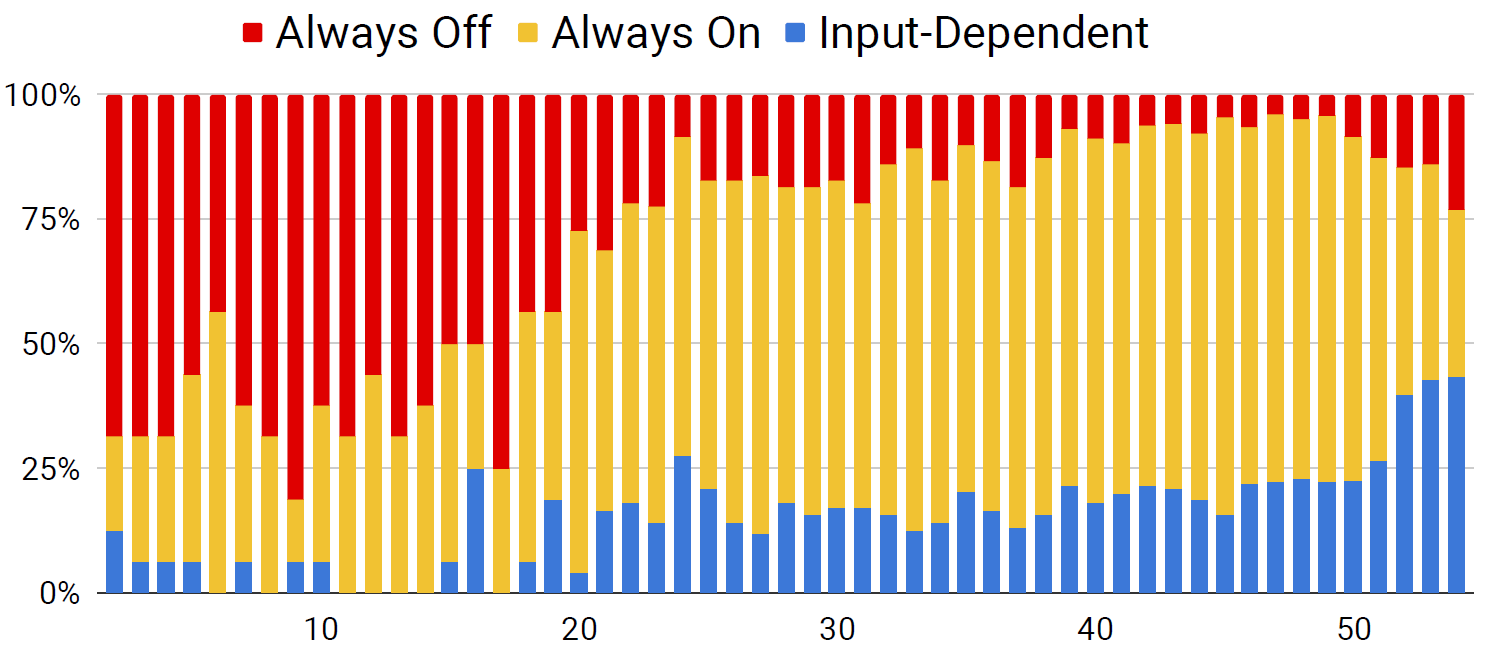
以及Input-Dependent门控的开启率分别情况:
同时还研究了不同sample开启的gating数量的分布情况(真的有点吃惊会是这么集中这么漂亮的一个分布)
作者还对CIFAR10上10个不同类别的图像,其对应的开启的门控做了聚类分析与PCA降维可视化:
可以看到不同类别的图像,其各自开启的门控有一定的规律与聚类中心,但也相对较散。作者认为GaterNet也就是Policy不应过度学习分类特征而,更多的应该关注门控的控制,这样的分布情况符合期望。
LC-Net(IJCAI2020)
论文:https://arxiv.org/pdf/2007.15151v1.pdf(单元/通道级条件计算)
《Fully Dynamic Inference with Deep Neural Networks》
感觉没什么新意
L-Net
残差单元级条件计算(这个ReLU1就很神奇)
作者用ReLU1说是因为这个不会遭受梯度消失。
C-Net
通道级条件计算(和上面这个真没什么差)
对于BasicBlock,mask和第一个3x3卷积的输出相乘;对于Bottleneck,mask和第一个1x1卷积的输出相乘。论文里面画的图有误!
训练方法
backbone的wd=5e-4,gate的wd=1e-5
直接对gate的输出加L1正则化
CondConv(NIPS2019)
论文:https://arxiv.org/pdf/1904.04971.pdf(条件模型集成)
这篇论文巧妙的地方在于应用了模型集成,但是利用卷积算子可以线性组合的特点,将个模型按层集成,每个卷积层中都将
套权重有条件地线性组合,得到一套新的、动态适配于输入的卷积权重,从而进行一次卷积操作就能实现条件模型集成效果:
其中是通过条件计算的Policy Network计算得出的。
被作为一套动态适配
于输入的权重,进行卷积运算。
不过由于在GPU上训练的时候大部分我们都是依batch训练的,但现在batch中的每个sample对应的卷积权重都不同,不能直接做并行运算。作者提出当时,每个CondConv层都连续做
次卷积后再进行加权(如下图左所示);而当
时,算出每个sample的权重再分别做batch_size=1的前向效率更高。(如下图右所示)
os:不过不论怎么说CondConv的训练一定会非常非常慢……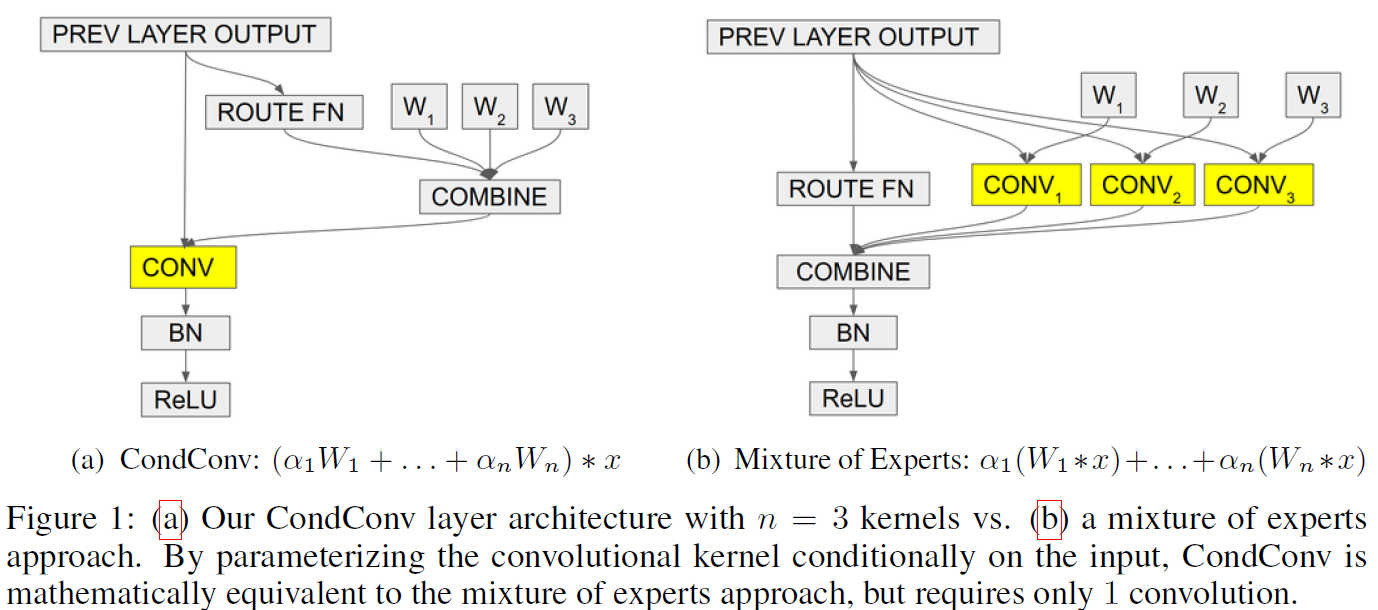
Ablation studies
上一节图中的COMBINE部分就是条件计算的Policy Network,仅仅由avgpool+fc+sigmoid构成。另外需要注意BN是加在combine之后的。
作者还尝试了在决策网络中再添加一个隐层的fc+relu以增强决策模块的拟合能力,但实验结果没什么效果。下表中Hidden (small)添加了宽度为channel_in / 8的隐层,(middle)添加了宽度为channel_in的隐层,(large)添加了宽度为channel_in * 8的隐层。
除此之外作者还尝试了把sigmoid换成softmax,也没有baseline好。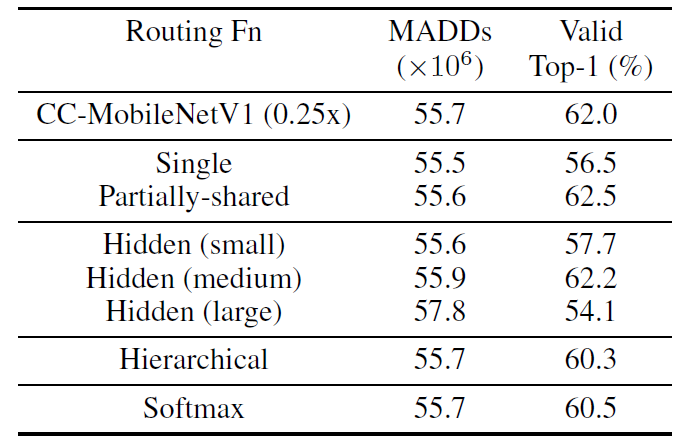
将CondConv应用到网络的不同位置,得到如下结果(标题表示从第多少个dw卷积开始应用CondConv):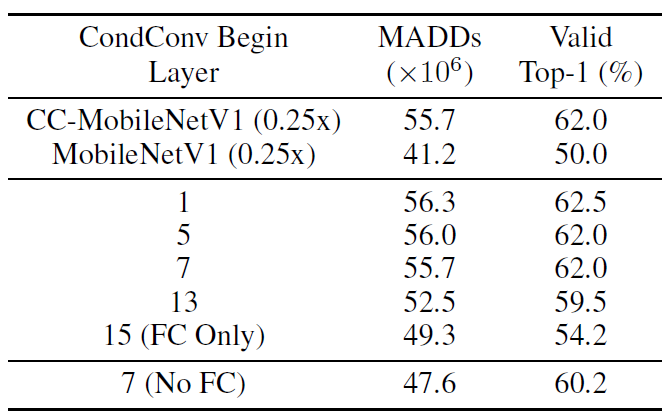
实验结果
作者基于MobileNet v1,用在ImageNet上进行了实验:(CondConv对dw卷积和fc依然可以使用,这里作者全部用了)

不同网络中,的实验结果:

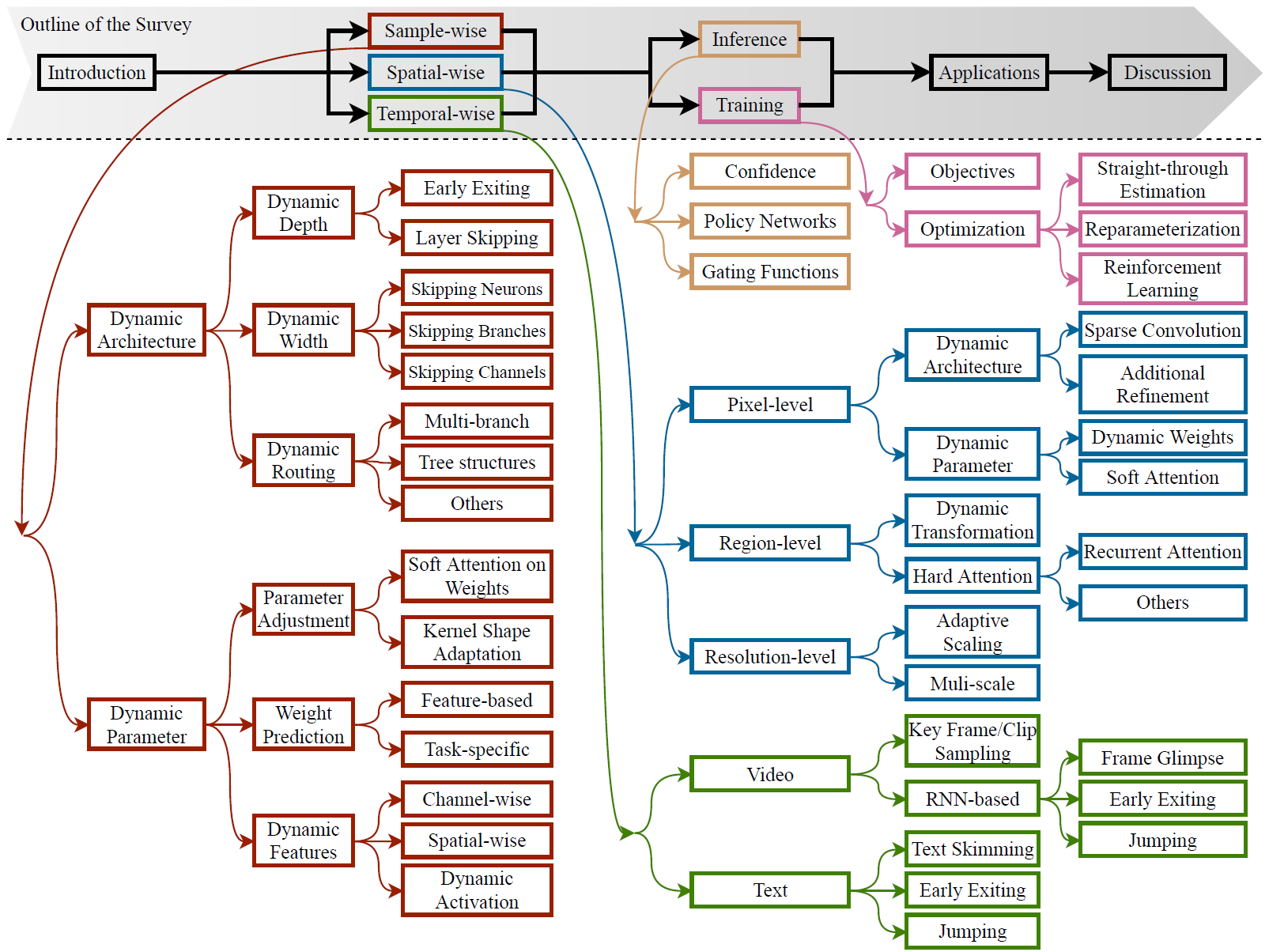
Dynamic Neural Networks(综述)
论文第一章对动态神经网络进行了介绍;第二章介绍了sample-wise动态神经网络;第三章与第四章分别介绍了spatial-wise(类似空间注意力,譬如Precision Gating)、temporal-wise(时间序列注意力,譬如丢掉不重要的视频帧)
动态神经网络的优点:
- 高效:对简单的输入,或信息量少的图像位置(Spatial),或序列中信息量少的节点(Temporal)不需要执行过多的冗余计算
- 表征能力强:推理计算量相同时模型容量更大
- 自适应:使得模型在不同算力约束下都能有良好表现
- 兼容性强:可以往里加其他优化方法
- 一般性强:动态神经网络技术可以应用到各种领域,譬如分类、检测、分割等
- 可解释性:动态神经网络的研究弥补了神经网络机制与脑科学间的空隙???(os:太厉害了)
Sample-wise动态
动态网络结构
动态深度
包括Early exiting、Layer skipping。其中Early exiting包括多个独立的神经网络级联(还真没见过)、中间分类器(类似自蒸馏)、多尺度结构。Layer skipping在CNN上作者只提到了SkipNet和BlockDrop。还有一种是基于Halting score的方法(和以前想的每个Block后拉一个分类器类似,但Halting score只算停止分不做预测)
多尺度结构的思路还挺新奇的,防止早期stage只有基础特征而被迫学习对最终任务直接起作用的特征而丢失了基础特征,影响整个网络的准确度: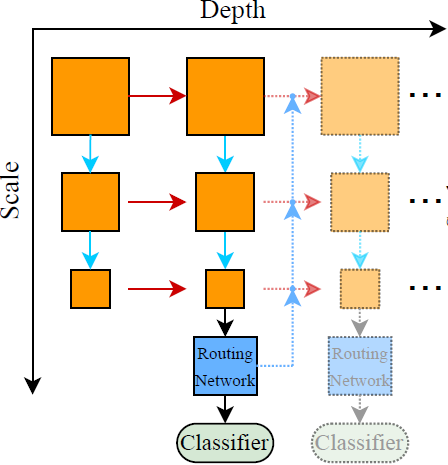
动态宽度
包括全连接跳节点(全连接都不太用了)、MoE的branch(mixture-of-experts多专家集成)、跳通道(比如上面写道的Channel Gating)
动态路径
譬如甚至有丧心病狂的在一个Block里堆了BasicBlock、Bottleneck、DWBottleneck等条件计算选路径……
因为和我想做的方向差的有点大,没仔细看
动态网络参数
权重的Attention
譬如CondConv,还有其它变形卷积学习卷积核形状的方法没仔细看
预测权重
直接用一个独立的模型预测runtime的参数(还能这么搞???)
论文:《Dynamic filter networks》(NIPS2016)
《Hypernetworks》(ICLR2016)
Loss设计技巧
做SkipNet等实验的时候,总是发现模型偏向于使用特定的Block,导致许多Block的激活率达到1.0而另外一些Block的激活率接近0.0,几乎算是被永久移除。
《OUTRAGEOUSLY LARGE NEURAL NETWORKS: THE SPARSELY-GATED MIXTURE-OF-EXPERTS LAYER》论文第四章中提出的方法是:
其中被称为变异系数(个人感觉直接用标准差也行),
为一个mini-batch中所有sample的门控输出之和,是一个长度等于门控数量的向量。
被用于减小每个门控的平均输出的离散程度(文中称为每个Block的平均重要程度),有点类似于下面提到的
取
时的效果。
这篇论文引用的另一篇论文,几乎也是用强化学习条件计算方面几乎是最早期的论文之一,《CONDITIONAL COMPUTATION IN NEURAL NETWORKS FOR FASTER MODELS》里提出了三个用于解决这个问题的loss:
这个loss被用于迫使每个mini-batch中,每个门控的平均激活率接近目标值。(有利于解决问题)
这个loss被用于迫使mini-batch中的每个sample平均门控激活率接近目标值。(相比SkipNet的辣鸡方法更易控制裁剪率)
↑↑↑↑↑ 以上两个loss在文中是被算在一起,受同一个加权超参控制的。
这个loss被用于迫使同一个gate对不同的输入输出不同的值。(有利于解决问题)
Ideas
- 把每个input在条件计算中用到了哪些block这个信息作为独热码,辅助分类器进行分类
- 预测每个Block的重要度进行排序,选择最重要的那些。(Kendall Tau correlation在《Residual Networks Behave Like Ensembles of Relatively Shallow Networks》中被用于衡量打乱Block顺序的程度)
- Res2Net也是多分支网络,可以用来做条件计算
- 竟然train set上的block重要度普遍绝对值,关注那些重要度出奇高的block,将其残差乘大于1的数
- loss的构建,用softmax(-policy_output) * imp的方法,会让模型只关注imp最低的那一个Block其它全部忽略。同样的,对于KL loss,plog(p/q),那些p比较小的项对loss的影响较小,也不会被关注?
- 比较iterative裁+finetune与iterative(裁+finetune)