二叉树的深度遍历和广度遍历

1. 深度优先遍历

1.1关于深度优先遍历

沿着树的深度遍历结点，尽可能深的搜索树的分支。如果当前的节点所在的边都被搜索过，就回溯到当前节点所在的那条边的起始节点。一直重复直到进行到发现源节点所有可达的节点为止。

1.2 算法实现

因为深度优先搜索算法是先访问根节点，接着遍历左子树再遍历右子树。为了方便，我们可以引入堆栈这个数据结构来帮我们快速解决DFS算法。因为栈是后进先出的结构，所以我们可以先将右子树压栈，再将左子树压栈，这样左子树就位于栈顶，可以保证先遍历左子树再遍历右子树。

我们通过下面的这个二叉树来简单的画图实现栈的深度优先搜索

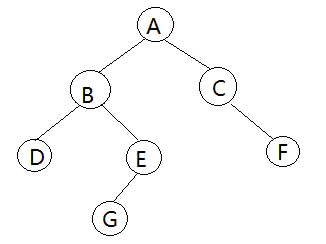
图1

当我们在压栈时，必须确保该节点的左右子树都为空，如果不为空就需要先将它的右子树压栈，再将左子树压栈。等左右子树都压栈之后，才将结点压栈。

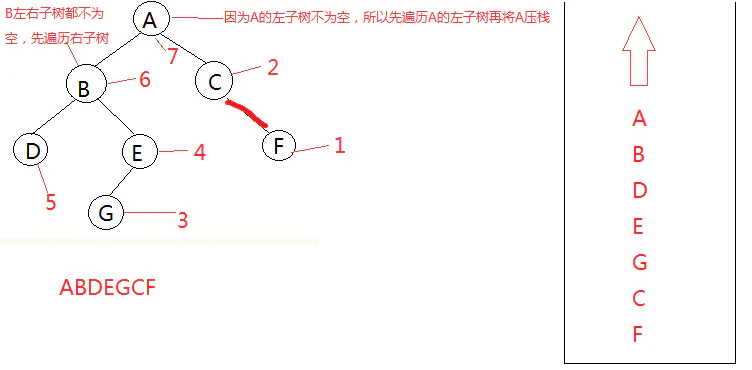
深度优先搜索

void depthFirstTravel(Node* root){
    stack<Node *> nodeStack;  //使用C++的STL标准模板库
    nodeStack.push(root);
    Node *node;
    while(!nodeStack.empty()){
        node = nodeStack.top();
        printf(format, node->data);  //遍历根结点
        nodeStack.pop();
        if(node->rchild){
            nodeStack.push(node->rchild);  //先将右子树压栈
        }
        if(node->lchild){
            nodeStack.push(node->lchild);  //再将左子树压栈
        }
    }
}

1.3 LeedCode上的一道简单DFS题

1. Employee Importance
   题目主要的意思是求出该员工的重要程度，给了员工类包含ID、重要度、下属。计算该员工的重要度不单单计算自己，还得将下属的重要度一起计算上。

解决方案

/*
// Employee info
class Employee {
public:
    // It's the unique ID of each node.
    // unique id of this employee
    int id;
    // the importance value of this employee
    int importance;
    // the id of direct subordinates
    vector<int> subordinates;
};
*/
class Solution {
public:
    unordered_map<int, Employee*> Emplmap;
    int getImportance(vector<Employee*> employees, int id) {
        for(int i=0;i<employees.size();i++)
        {
            Emplmap[employees[i]->id]=employees[i];
        }       
        return DFS(Emplmap[id]);
    }
    int DFS(Employee* empl)
    {
        int sum = empl->importance;
        for(int i = 0;i<empl->subordinates.size();i++)
        {
            sum+=DFS(Emplmap[empl->subordinates[i]]);
        }
        return sum;
    }
};

2. 广度优先遍历

2.1关于广度优先遍历

从根节点开始，沿着树的宽度遍历树的节点，直到所有节点都被遍历完为止。

2.2 算法实现

因为是按照一层一层遍历的，所以我们考虑引入队列这个数据结构帮助我们实现广度优先搜索算法。

树的层次遍历

void breadthFirstTravel(Node* root){
queue<Node *> nodeQueue;  //使用C++的STL标准模板库
    nodeQueue.push(root);
    Node *node;
    while(!nodeQueue.empty()){
        node = nodeQueue.front();
        nodeQueue.pop();
        printf(format, node->data);
        if(node->lchild){
            nodeQueue.push(node->lchild);  //先将左子树入队
        }
        if(node->rchild){
            nodeQueue.push(node->rchild);  //再将右子树入队
        }
    }
}

2.3 LeedCode上的一道简单广度搜索的题

给出一棵二叉树，返回其节点值从底向上的层次序遍历
解决方法：和上面的实现方式类似，只是最后需要把容器翻转过来。

/**
 * Definition of TreeNode:
 * class TreeNode {
 * public:
 *     int val;
 *     TreeNode *left, *right;
 *     TreeNode(int val) {
 *         this->val = val;
 *         this->left = this->right = NULL;
 *     }
 * }
 */
class Solution {
    /**
     * @param root : The root of binary tree.
     * @return : buttom-up level order a list of lists of integer
     */
public:
    vector<vector<int>> levelOrderBottom(TreeNode *root) {
        vector<vector<int>> vec;
        if(root==NULL){
            return vec;
        }
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            int count=que.size();
            vector<int> vec_temp;
            while(count--){
                TreeNode* temp=que.front();
                que.pop();
                vec_temp.push_back(temp->val);
                if(temp->left){
                    que.push(temp->left);
                }
                if(temp->right){
                    que.push(temp->right);
                }
            }
            vec.push_back(vec_temp);
        }
        reverse(vec.begin(),vec.end());
        return vec;
    }
};