6.4 n 维列表

再往下钻，让我们为层次结构添加更多层。数据结构可以扩展到远超二维列表的列表。由于列表是 Dynamo 中的项目，而且它们本身也是项目，因此我们可以创建尽可能多维的数据。
我们将在此处使用的类比是俄罗斯套娃。每个列表可视为一个包含多个项的容器。每个列表都有自己的属性，也被视为自己的对象。

一组俄罗斯套娃（照片由 Zeta 提供）是 n 维列表的类比。每个层表示一个列表，每个列表在其中包含项目。在 Dynamo 的情况下，每个容器内可以有多个容器（表示每个列表的项目）。

n 维列表很难用直观的方式进行解释，但是我们在本章中设置了一些练习，这些练习着重于处理超出二维范围的列表。

映射和组合

映射无疑是 Dynamo 中数据管理最复杂的部分，并且在处理列表的复杂层次结构时尤其重要。在下面的一系列练习中，我们将演示在数据变为多维时何时使用映射和组合。
在上一节中，可以找到 List.Map 和 List.Combine 的初步介绍。在下面的最后一个练习中，我们将对复杂数据结构使用这些节点。

练习 - 二维列表 - 基本

下载本练习随附的示例文件（单击鼠标右键，然后单击“将链接另存为…”）。 1.n-Dimensional-Lists.dyn 2.n-Dimensional-Lists.sat

本练习是三个练习中的第一个，侧重于阐述输入的几何图形。本系列练习中的每个部分都将增加数据结构的复杂性。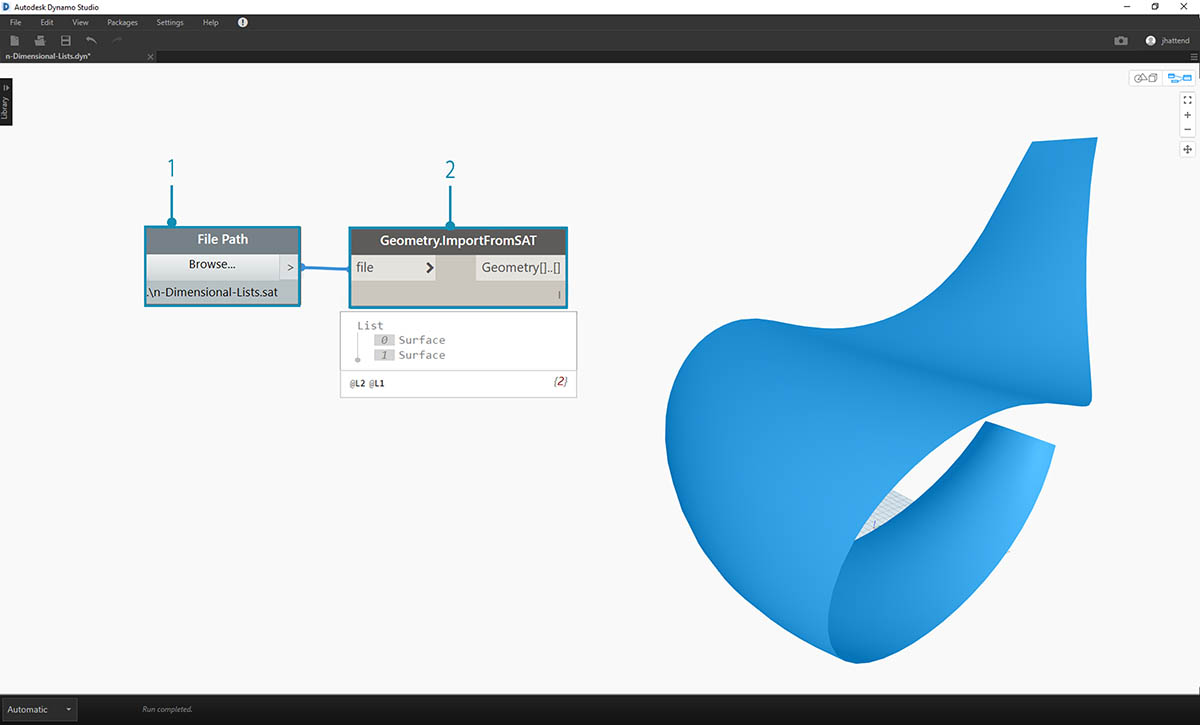

1. 让我们从练习文件文件夹中的 .sat 文件开始。我们可以使用“文件路径”(File Path) 节点抓取此文件。
2. 使用 Geometry.ImportFromSAT，该几何图形将作为两个曲面输入到 Dynamo 预览中。

在本练习中，我们希望保持简单并处理其中一个曲面。

1. 让我们选择索引 1 以抓取上方曲面。我们使用 List.GetItemAtIndex 节点来执行此操作。

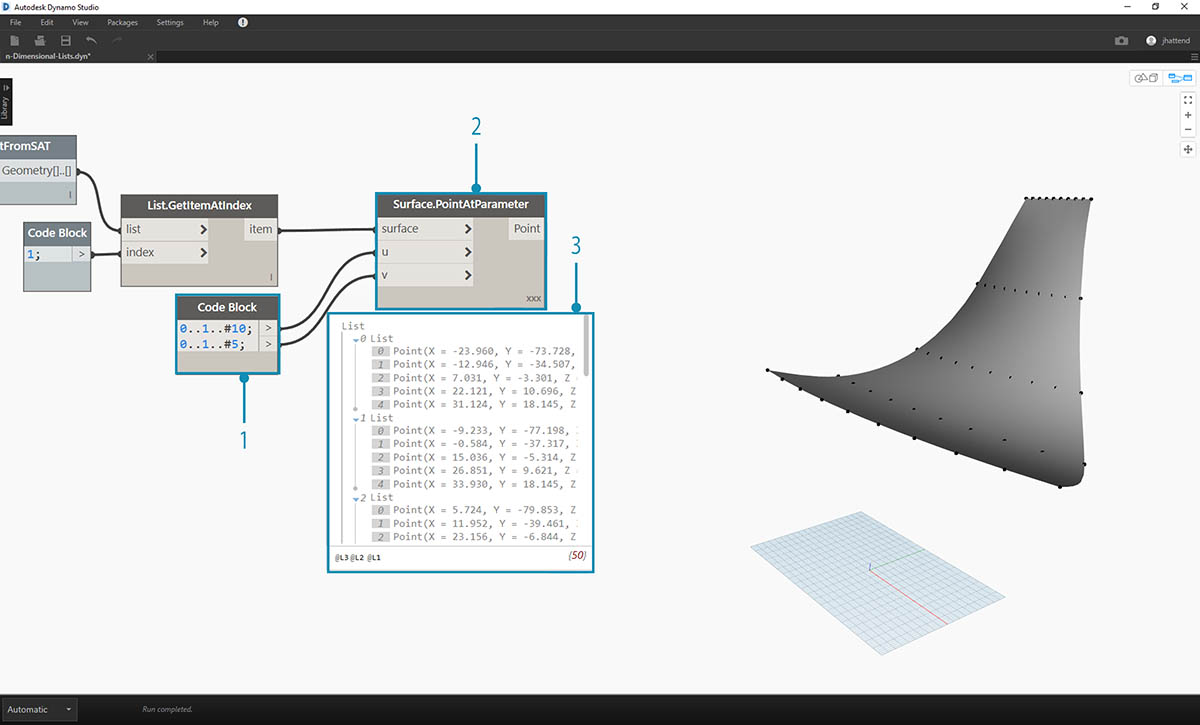
下一步是将曲面分割为点栅格。

1. 使用代码块，插入以下两行代码：

0..1..#10;
0..1..#5;

1. 使用 Surface.PointAtParameter，将两个代码块值连接到 u 和 v。将此节点的连缀更改为“叉积”。
2. 输出显示数据结构，这在 Dynamo 预览中也可见。

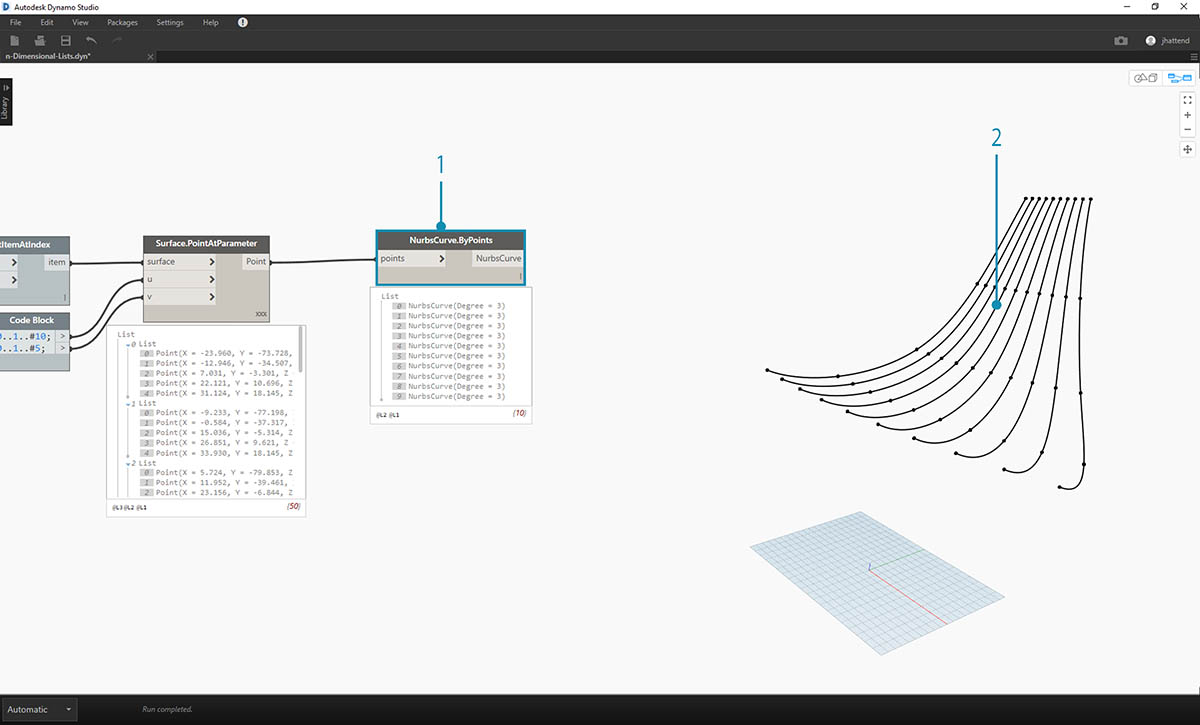
1. 要了解数据结构的组织方式，我们将 NurbsCurve.ByPoints 连接到 Surface.PointAtParameter 的输出。
2. 注意，我们有十条曲线沿曲面垂直延伸。

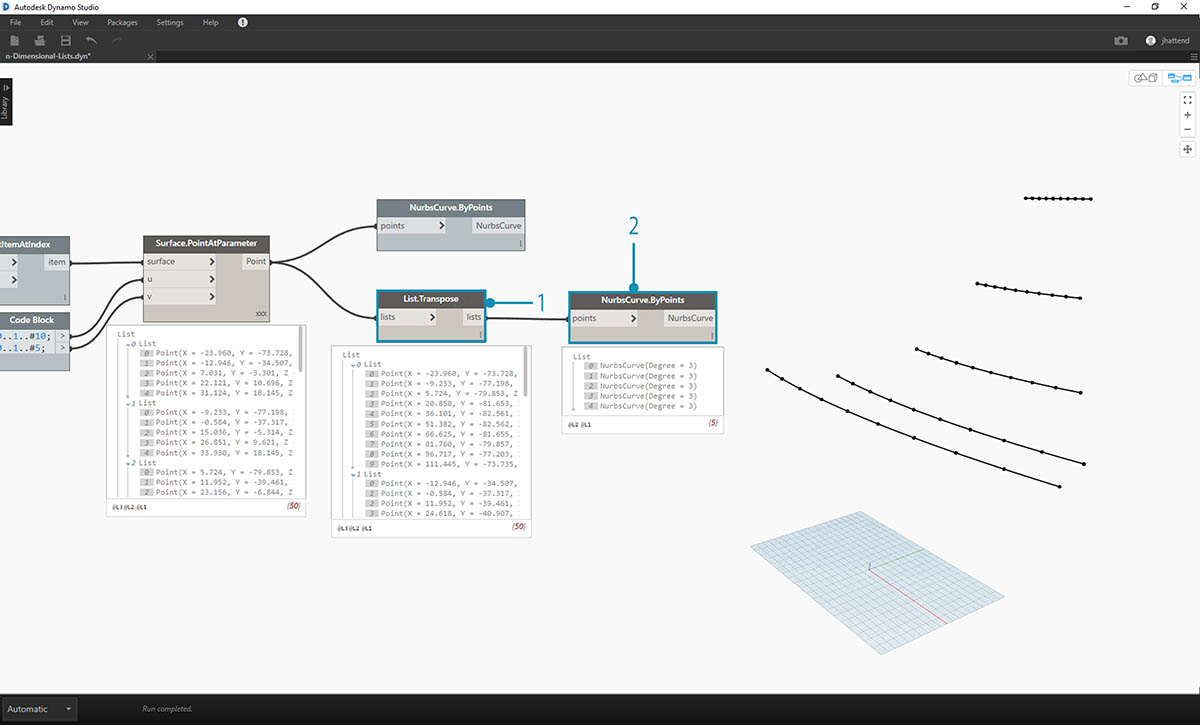
1. 基本 List.Transpose 将翻转一列列表的列和行。
2. 通过将 List.Transpose 的输出连接到 NurbsCurve.ByPoints，我们现在得到五条曲线在整个曲面上水平延伸。

练习 - 二维列表 - 高级

让我们增加复杂性。假定我们要对上一个练习中创建的曲线执行操作。也许，我们希望将这些曲线与其他曲面相关联，并在它们之间进行放样。这需要更加注意数据结构，但基本逻辑是相同的。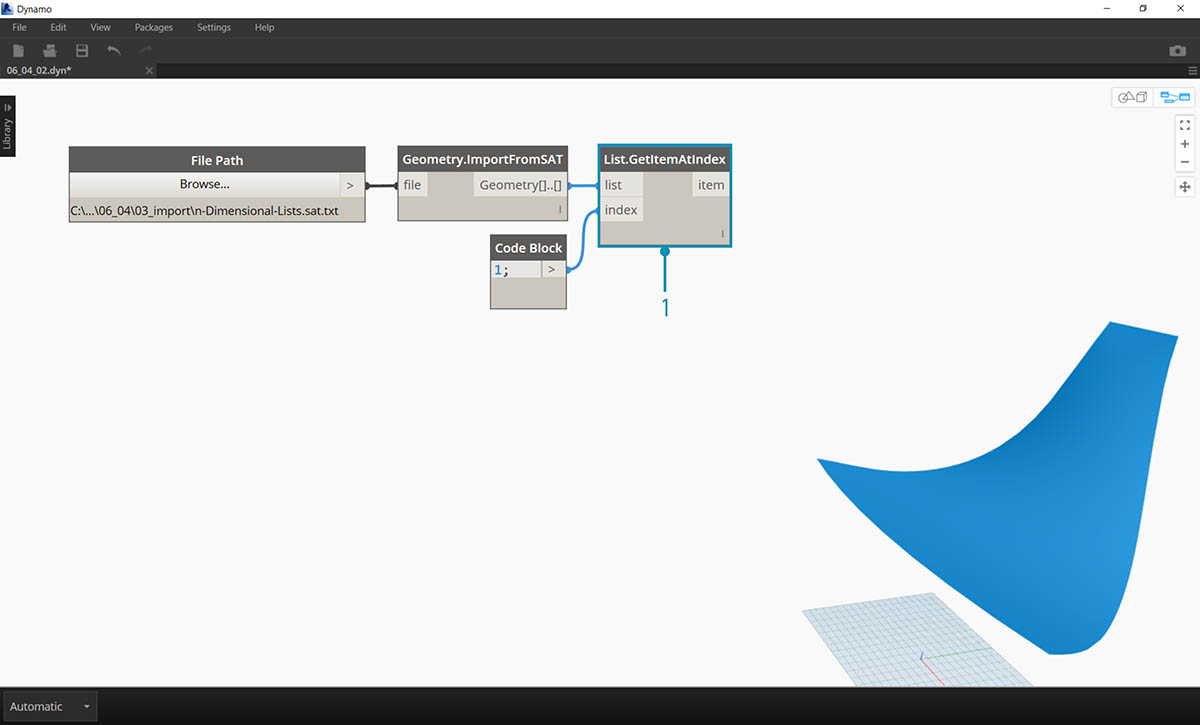

1. 从上一练习的步骤开始，使用 List.GetItemAtIndex 节点隔离已输入几何图形的上曲面。

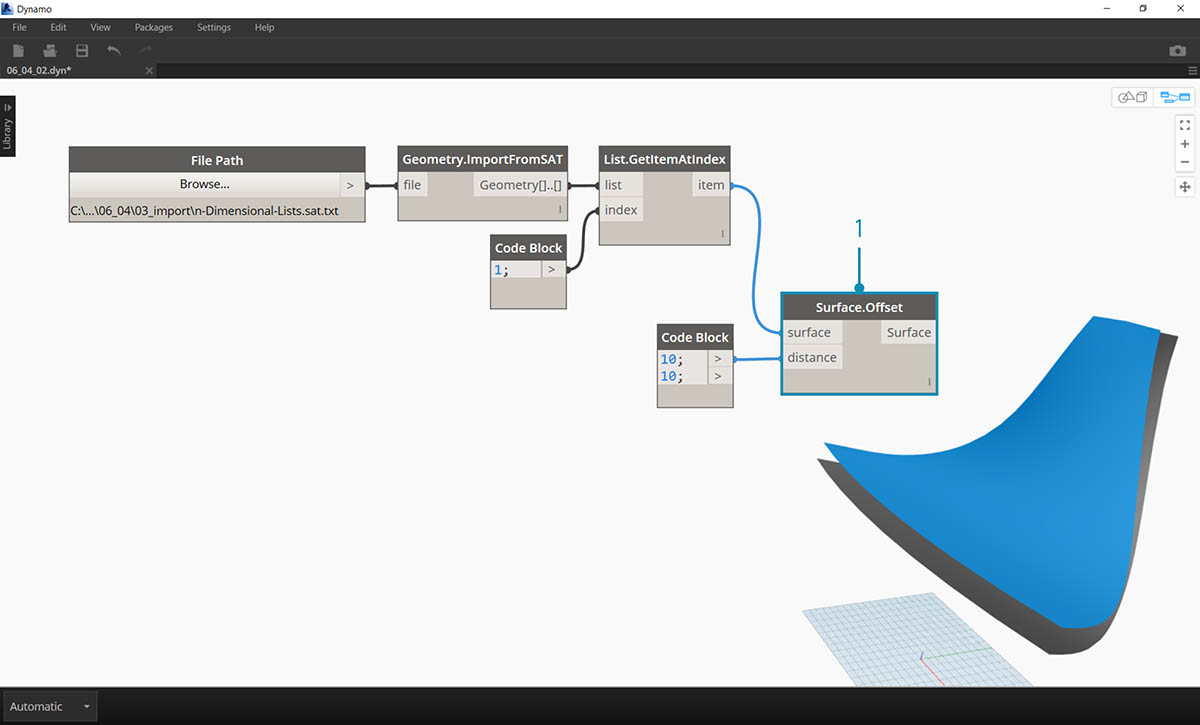
1. 使用 Surface.Offset，将曲面偏移值 10。

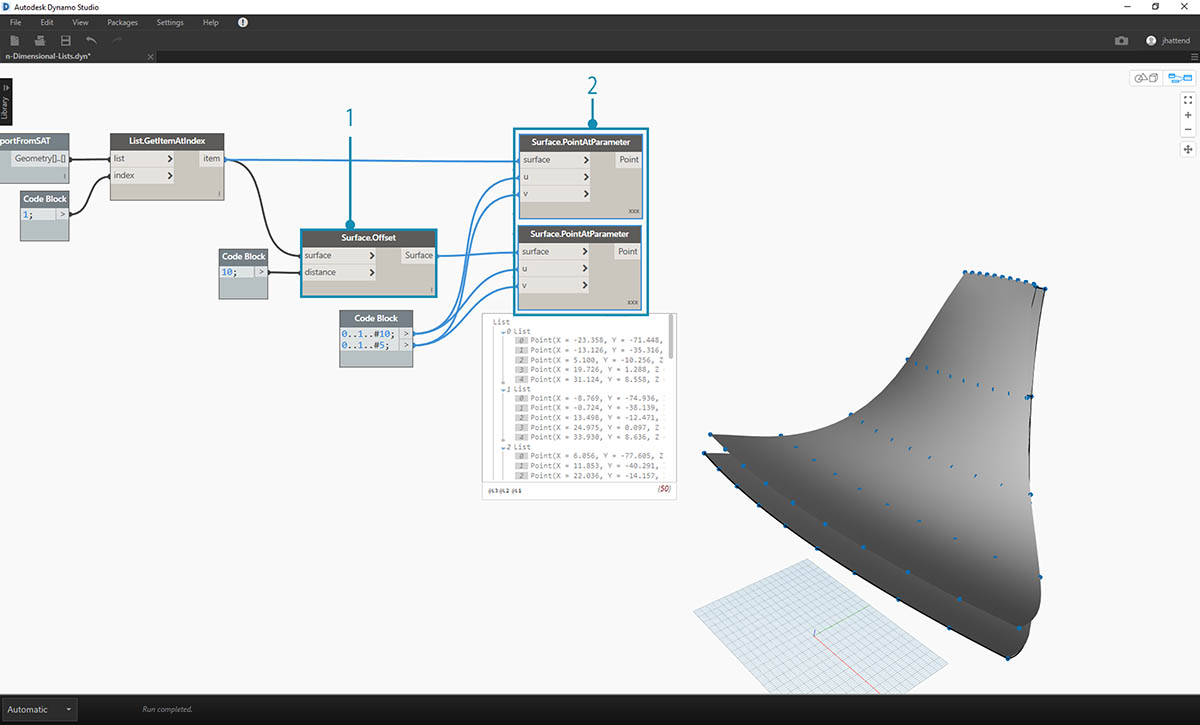
1. 按照与上一练习相同的方式，使用以下两行代码定义代码块：

0..1..#10;
0..1..#5;

1. 将这些输出连接到两个 Surface.PointAtParameter 节点，每个节点的连缀设置为“叉积”。其中一个节点连接到原始曲面，而另一个节点连接到偏移曲面。

1. 与上一练习中一样，将输出连接到两个 NurbsCurve.ByPoints 节点。
2. Dynamo 预览中显示与两个曲面对应的两条曲线。

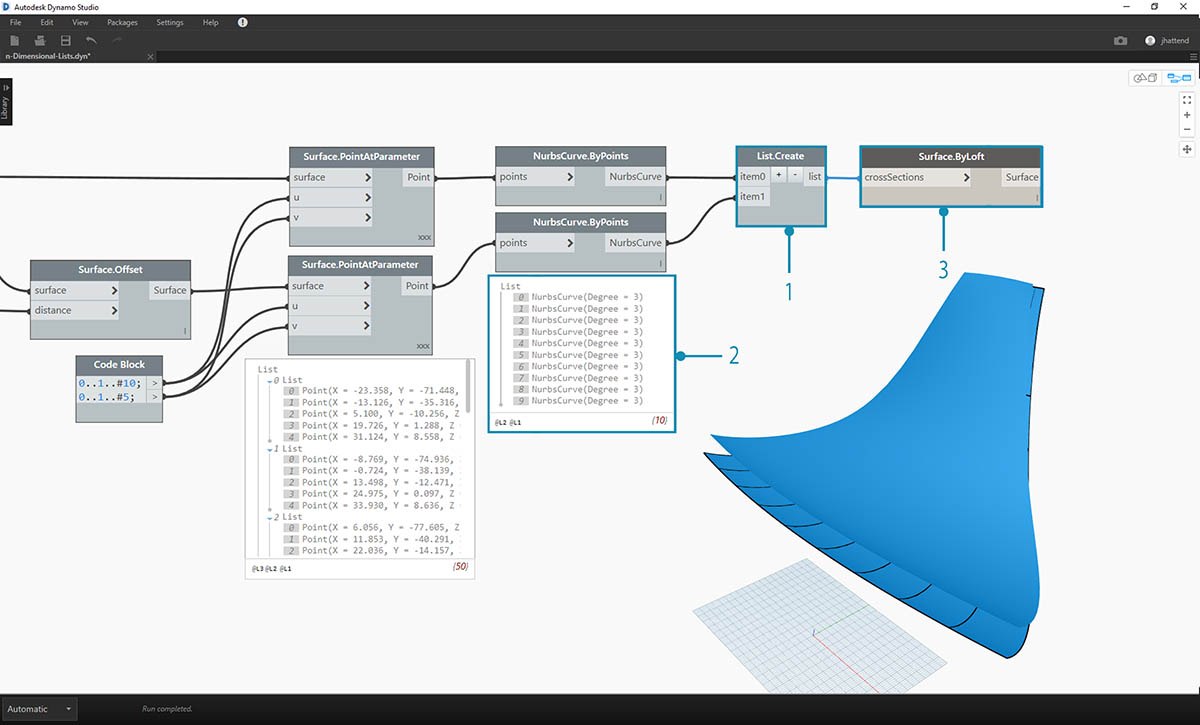
1. 通过使用 List.Create，我们可以将两组曲线合并为一列列表。
2. 在输出中注意到，我们有两个列表，每个列表包含十个项目，分别表示每个 NURBS 曲线的连接集。
3. 通过执行 Surface.ByLoft，我们可以直观地了解此数据结构。该节点将放样每个子列表中的所有曲线。

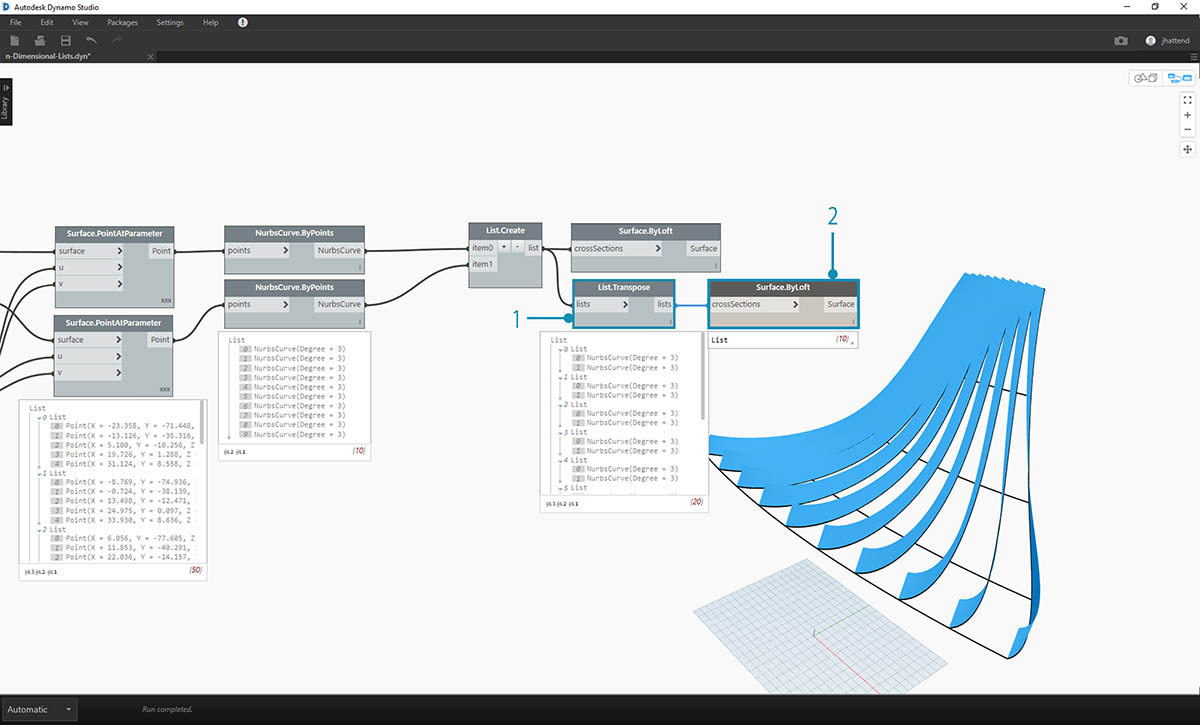
1. 通过使用 List.Transpose，请记住，我们将翻转所有列和行。此节点会将两列（每个列表十条曲线）转换为十列（每个列表两条曲线）。现在，我们得到与另一个曲面上的相邻曲线相关的每条 NURBS 曲线。
2. 使用 Surface.ByLoft，我们得到一个带肋的结构。

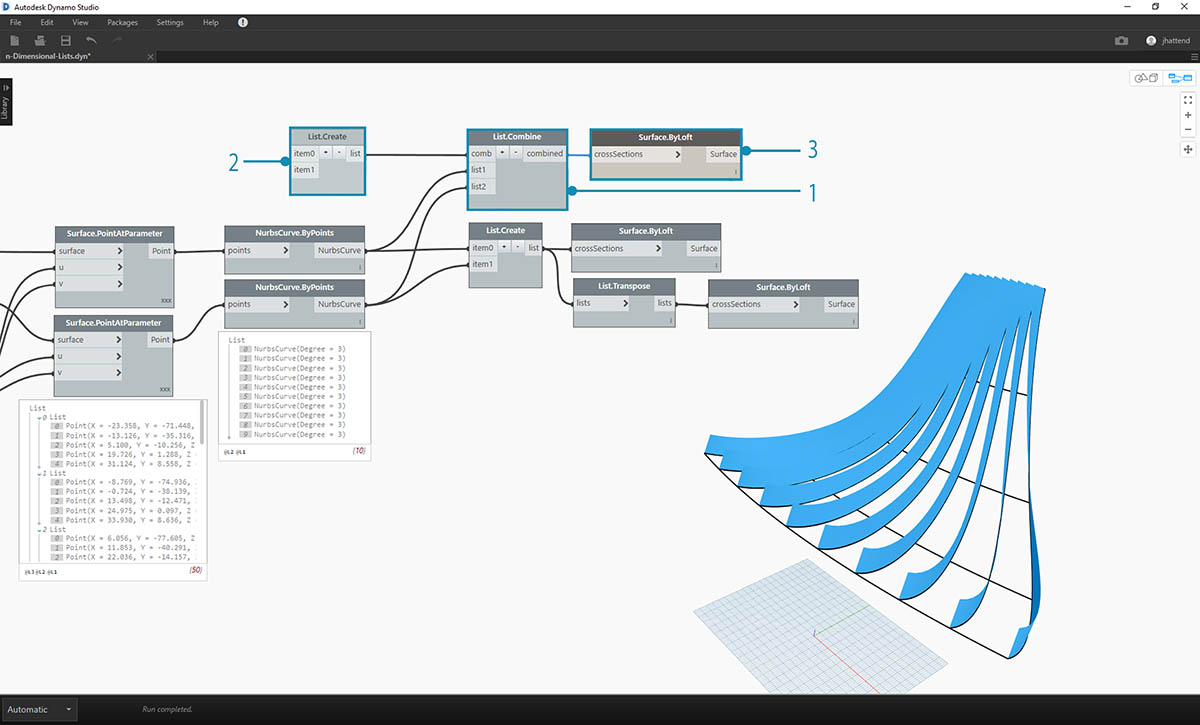
1. 除 List.Transpose 之外，还可以使用 List.Combine。这将对每个子列表运算“连结符”。
2. 在本例中，我们使用 List.Create 作为“连结符”，这将在子列表中创建每个项目的列表。
3. 使用 Surface.ByLoft 节点，我们得到与上一步中相同的曲面。在这种情况下，转置更容易使用，但当数据结构变得更加复杂时，List.Combine 更加可靠。

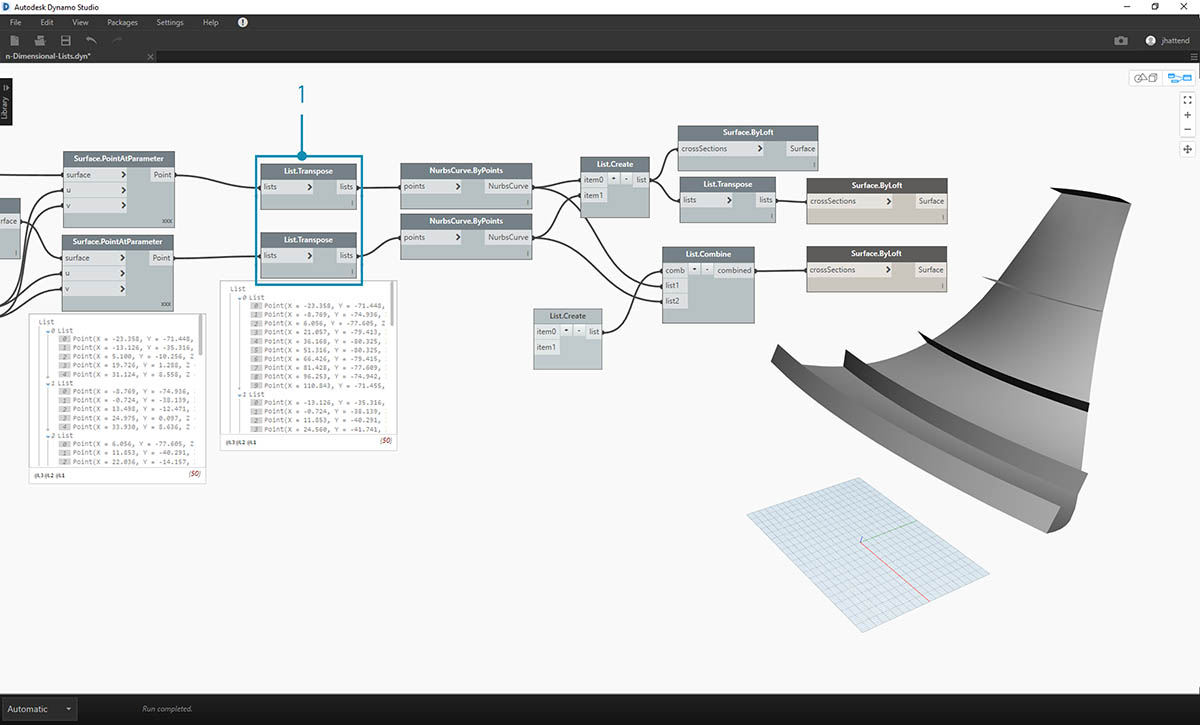
1. 如果要切换带肋结构中曲线的方向，请后退几步，我们需要先使用 List.Transpose，然后再连接到 NurbsCurve.ByPoints。这将翻转列和行，从而得到 5 个水平加强筋。

练习 - 三维列表

现在，我们将更进一步。在本练习中，我们将使用两个输入的曲面，从而创建复杂的数据层次结构。尽管如此，我们的目标是使用相同的基础逻辑来完成相同的操作。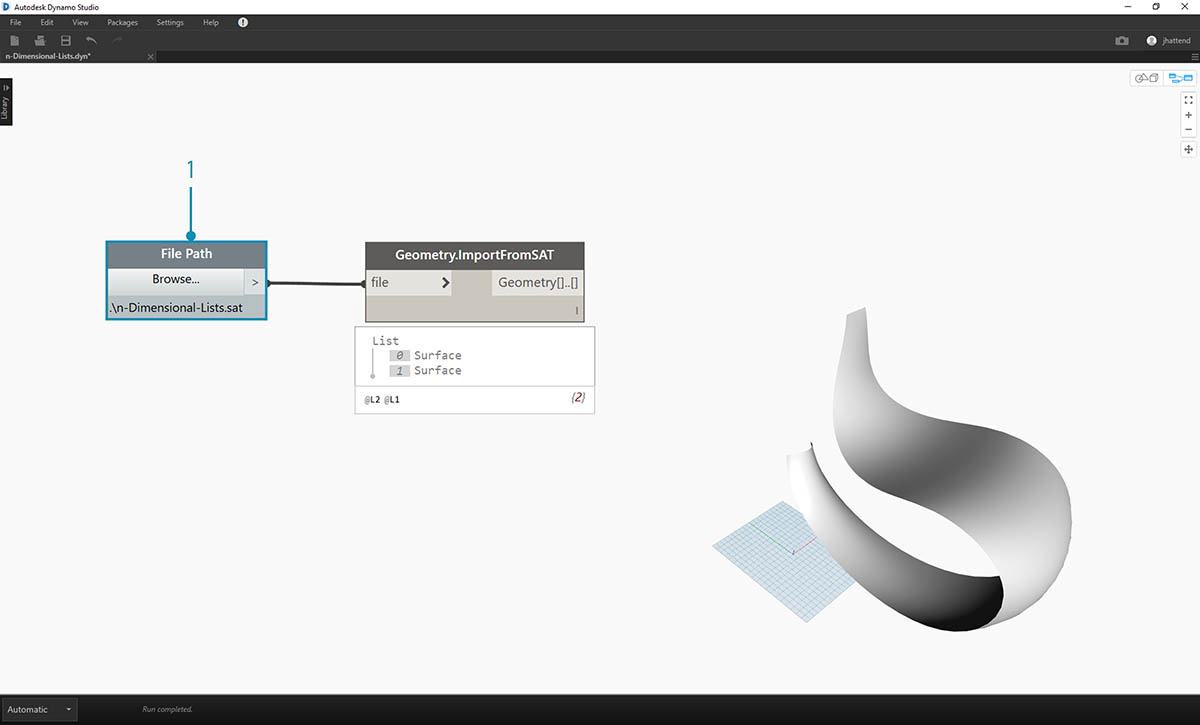

1. 从上一练习中输入的文件开始。

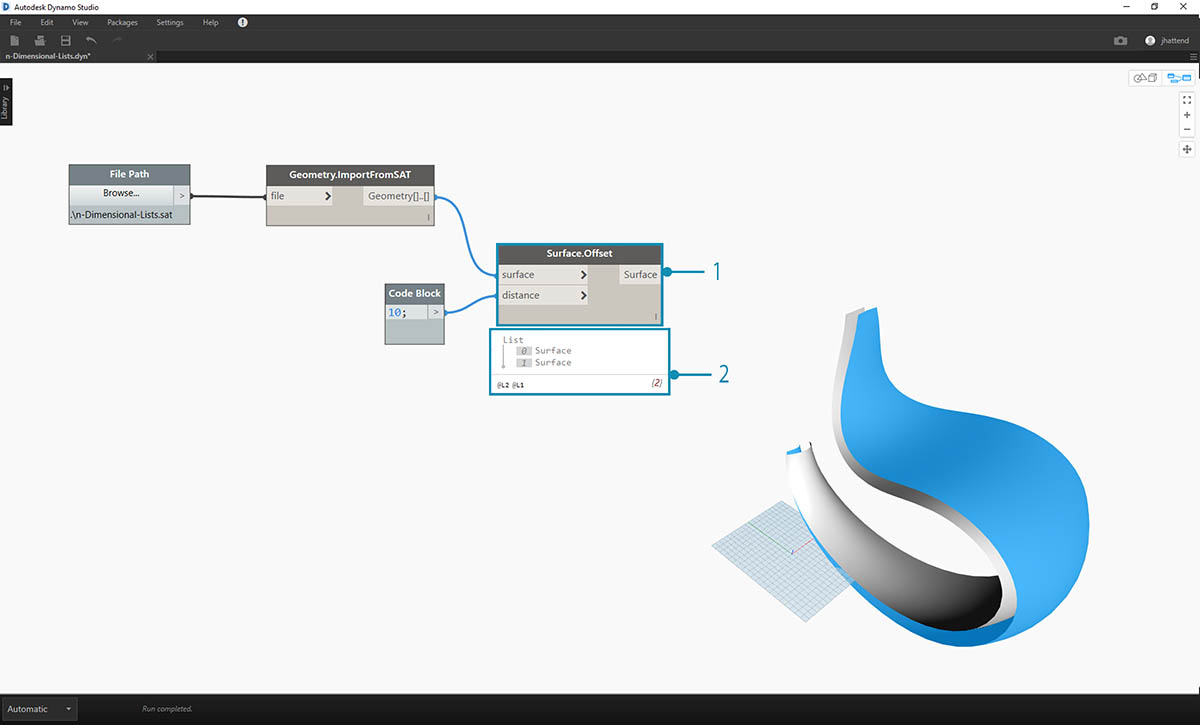
1. 与上一练习中一样，使用 Surface.Offset 节点按值 10 进行偏移。
2. 在输出中注意到，我们创建了两个具有偏移节点的曲面。

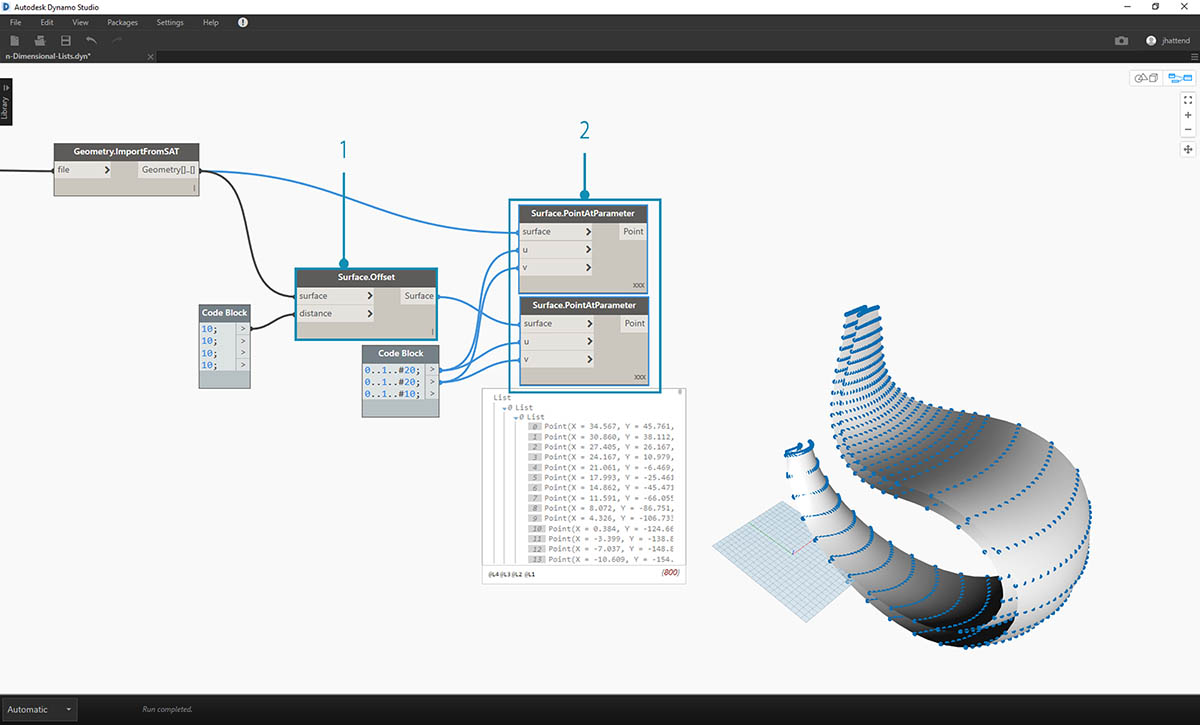
1. 按照与上一练习相同的方式，使用以下两行代码定义代码块：

0..1..#20;
0..1..#10;

1. 将这些输出连接到两个 Surface.PointAtParameter 节点，每个节点的连缀设置为“叉积”。其中一个节点连接到原始曲面，而另一个节点连接到偏移曲面。

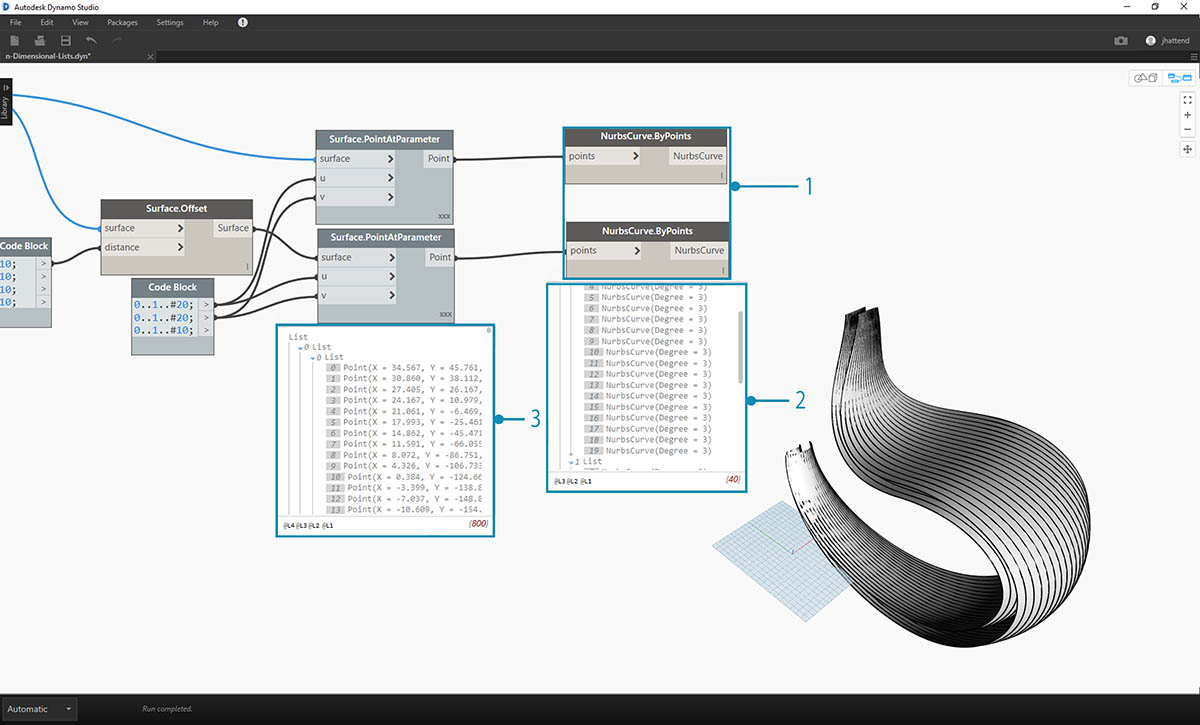
1. 与上一练习中一样，将输出连接到两个 NurbsCurve.ByPoints 节点。
2. 查看 NurbsCurve.ByPoints 的输出，注意到这是一列两个列表，比上一练习更复杂。数据按基础曲面分类，因此我们为结构化数据添加了另一个层级。
3. 请注意，Surface.PointAtParameter 节点中的对象变得更加复杂。在本例中，我们得到一列列表（其中每个元素也是一个列表）。

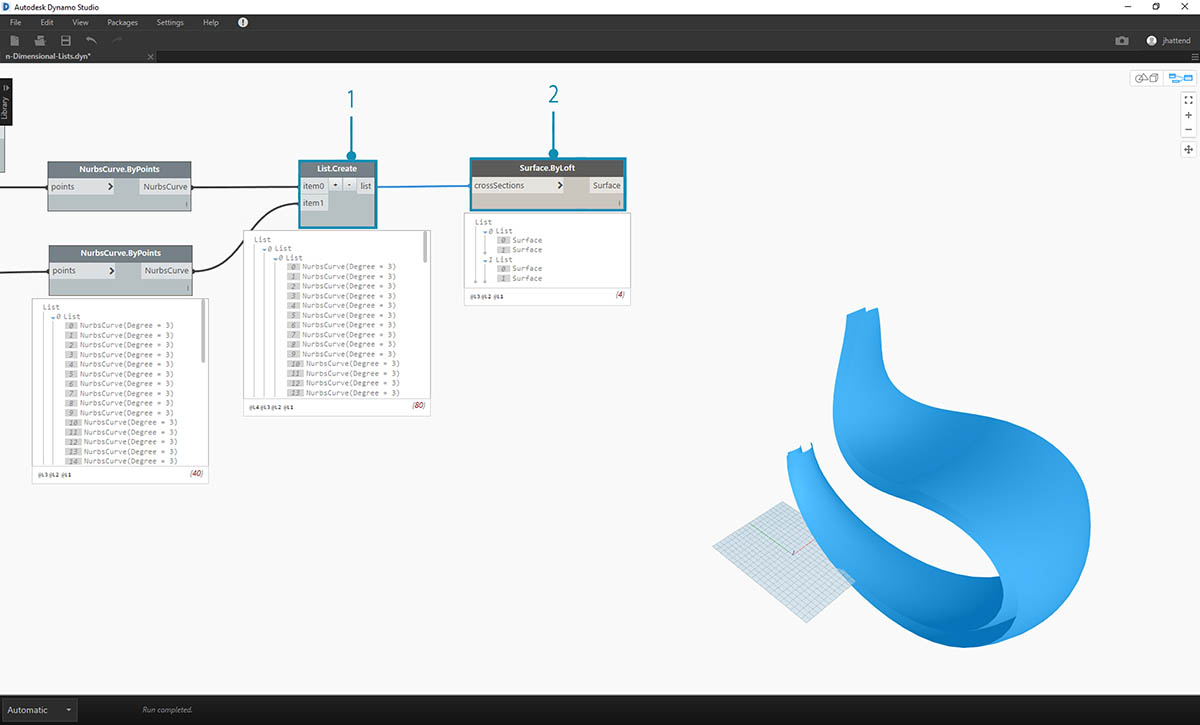
1. 使用 List.Create 节点，我们将 NURBS 曲线合并为一个数据结构，从而创建一列列表（其中每个元素也是一个列表）。
2. 通过连接 Surface.ByLoft 节点，我们得到原始曲面的版本，因为它们各自保留在由原始数据结构创建的自己列表中。

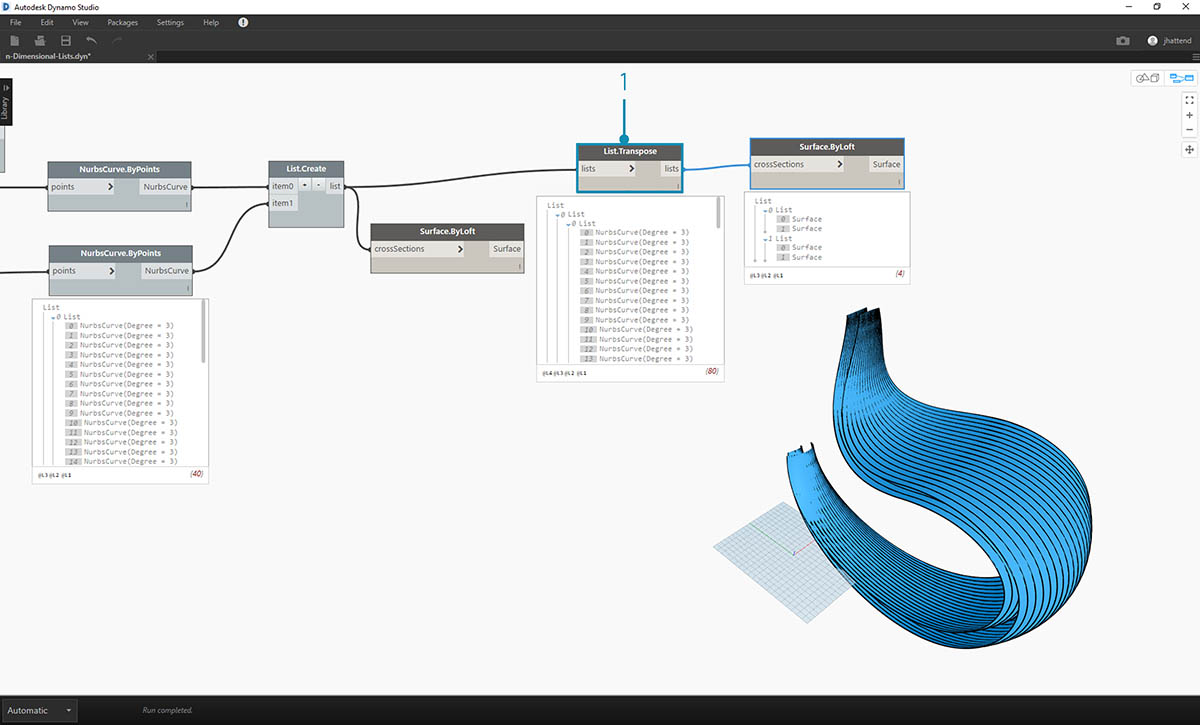
1. 在上一练习中，我们能够使用 List.Transpose 创建带肋结构。这在此处不起作用。对二维列表应使用转置，但由于我们有三维列表，因此“翻转列和行”操作不会像之一样轻松。请记住，列表是对象，因此 List.Transpose 将翻转包含子列表的列表，但不会将 NURBS 曲线在层次结构中进一步向下翻转一个列表。

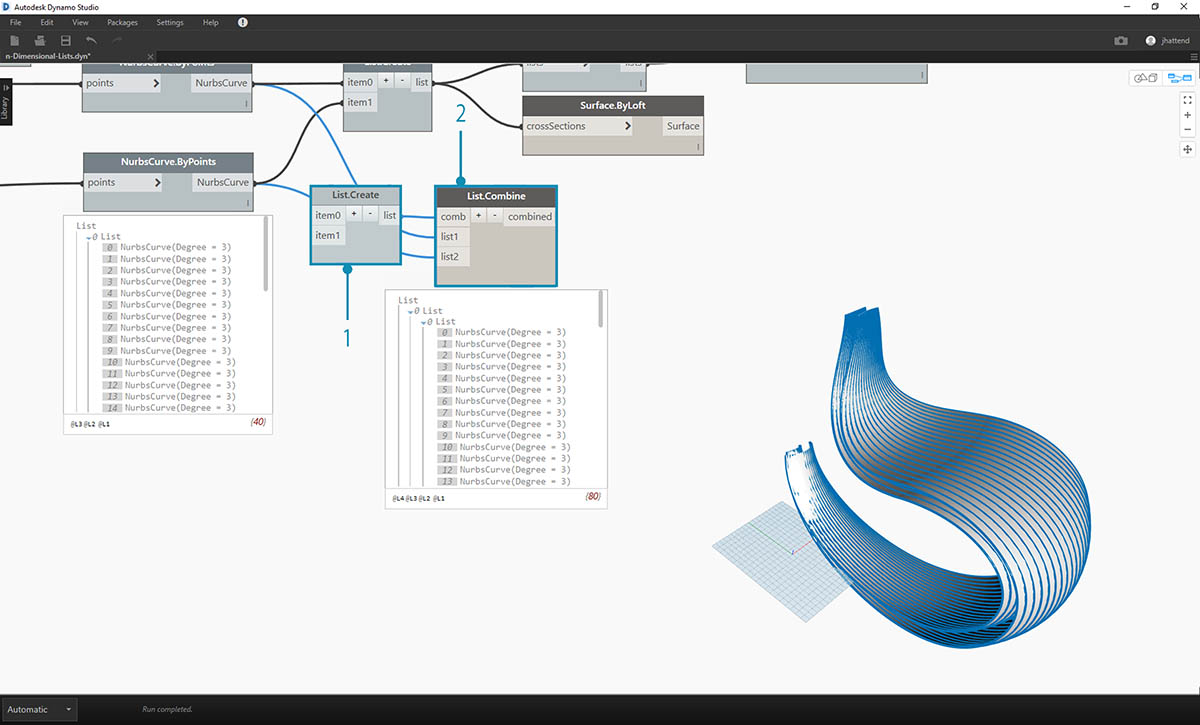
1. List.Combine 在此处将更加适用。当访问更复杂的数据结构时，我们要使用 List.Map 和 List.Combine 节点。
2. 使用 List.Create 作为“连结符”，我们可以创建一个数据结构，使其更加适用。

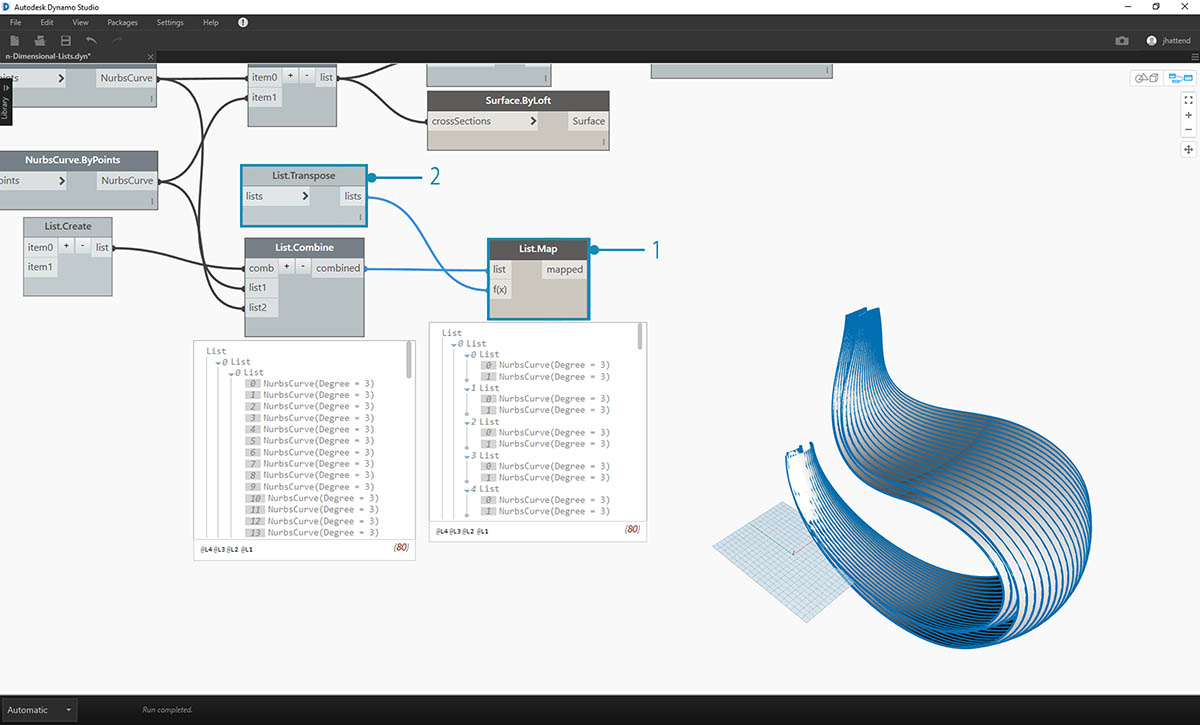
1. 数据结构仍需要在层次结构上向下转置一步。为此，我们将使用 List.Map。除了使用一个输入列表（而不是两个或更多）之外，这类似于使用 List.Combine。
2. 我们将应用于 List.Map 的函数是 List.Transpose，这将翻转主列表中子列表的列和行。

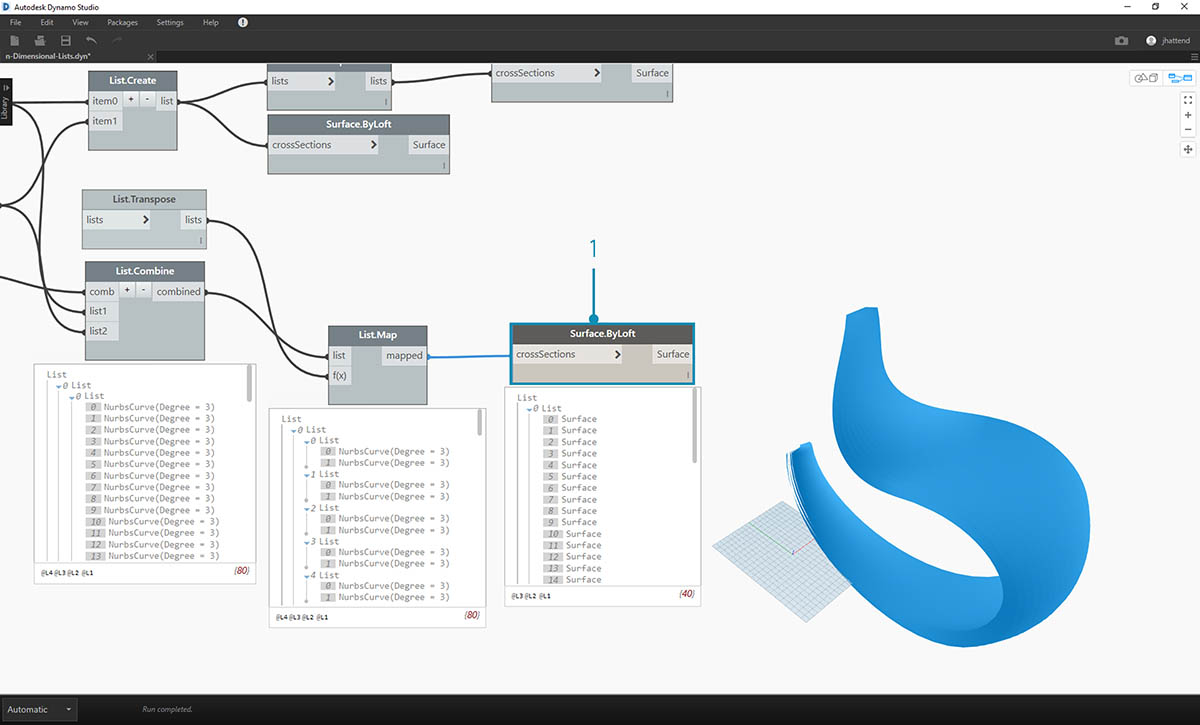
1. 最后，我们可以结合使用正确的数据层次结构放样 NURBS 曲线，从而提供带肋结构。

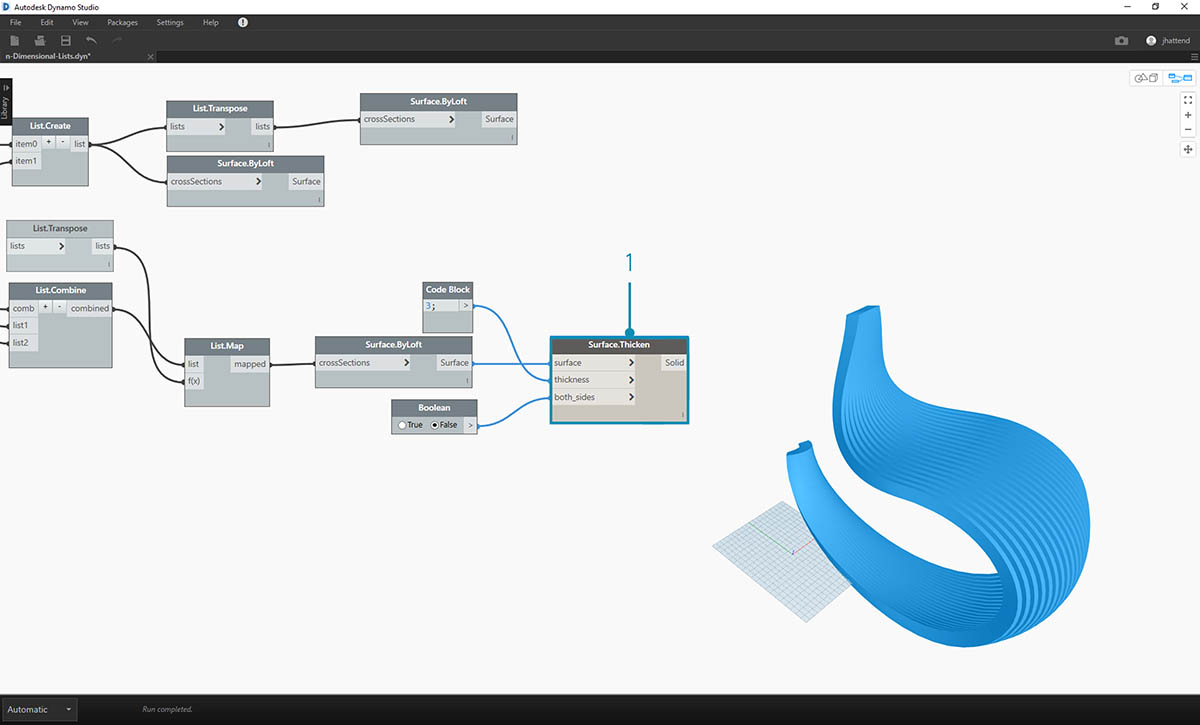
1. 让我们使用 Surface.Thicken 节点为几何图形添加一些深度。

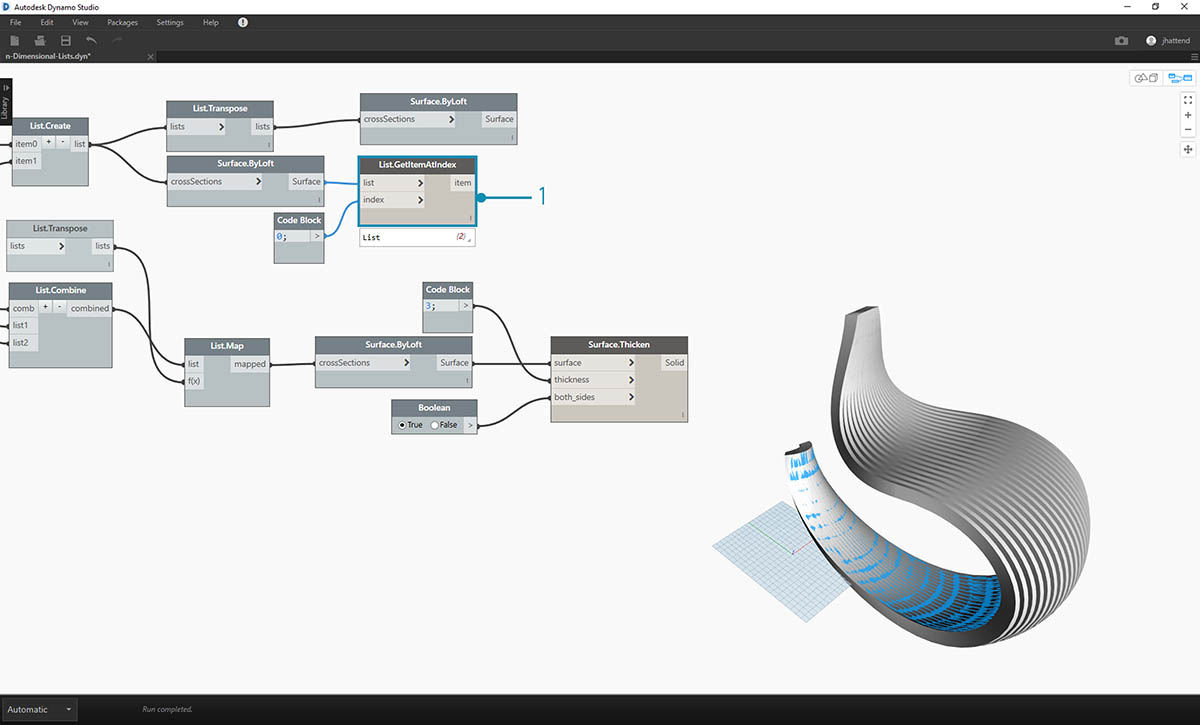
1. 最好在此结构中后退两步添加曲面，以便将使用 List.GetItemAtIndex 来从以前步骤的放样曲面中选择后曲面。

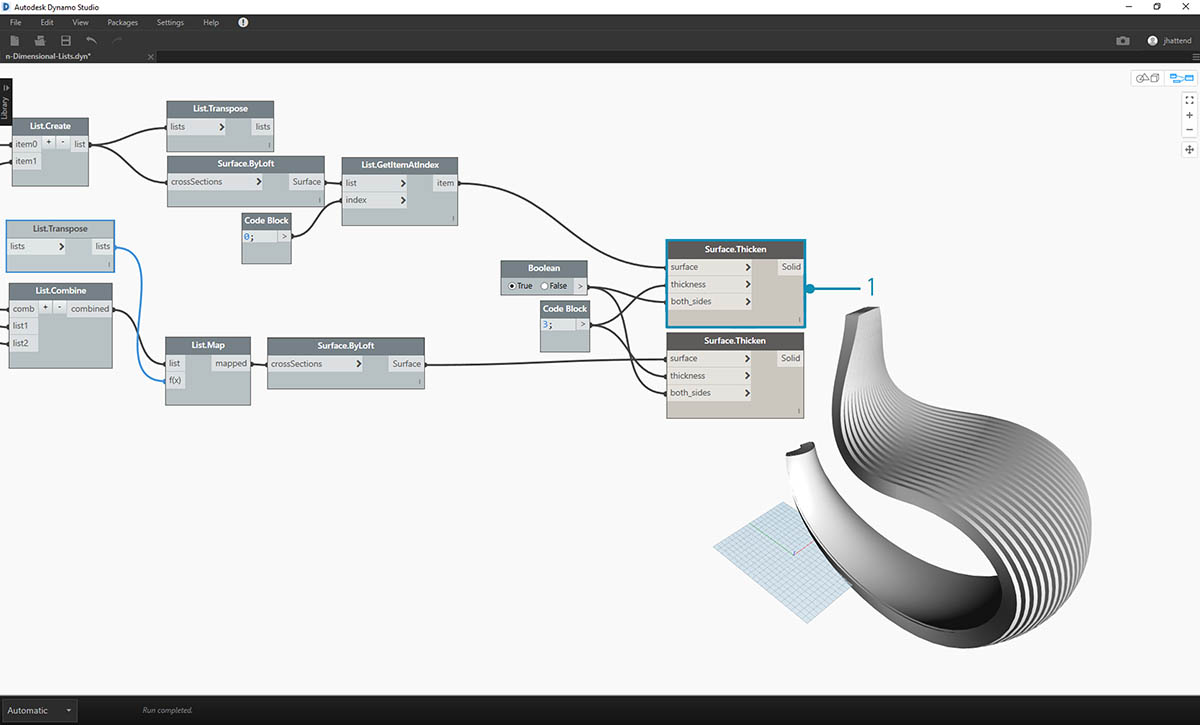
1. 加厚这些选定曲面，完成连接。

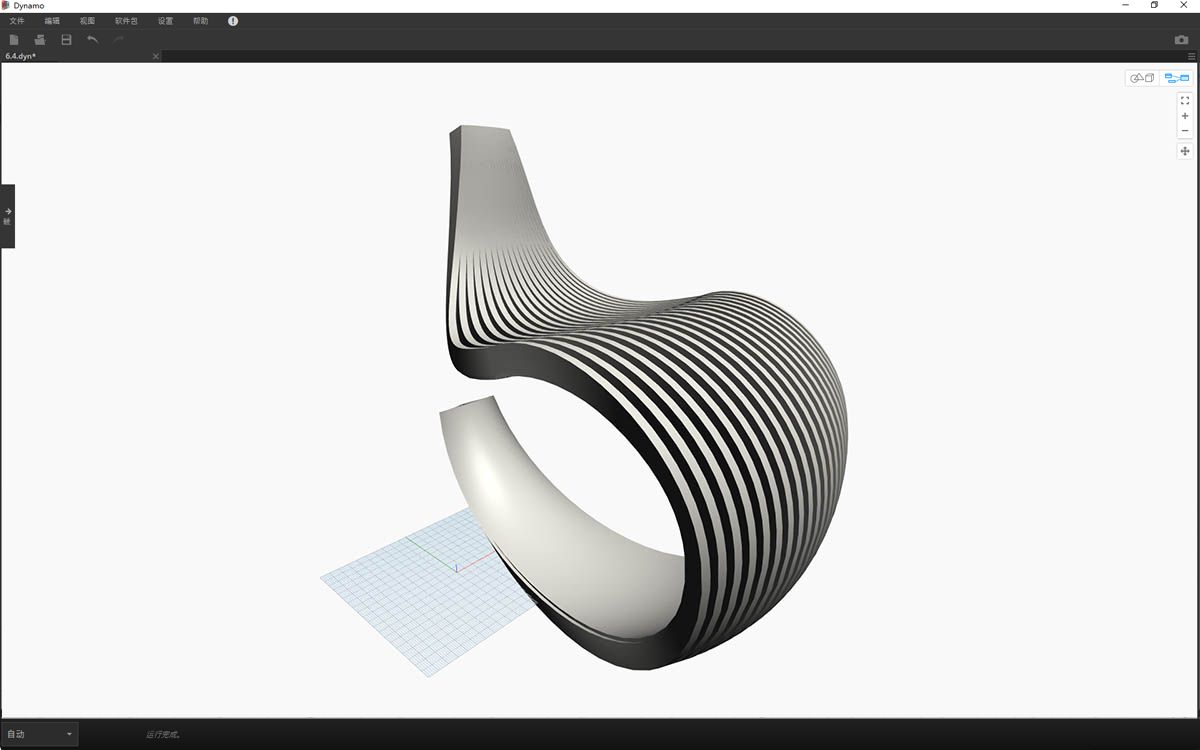
这不是有史以来最舒适的摇椅，但还会进行大量数据处理。

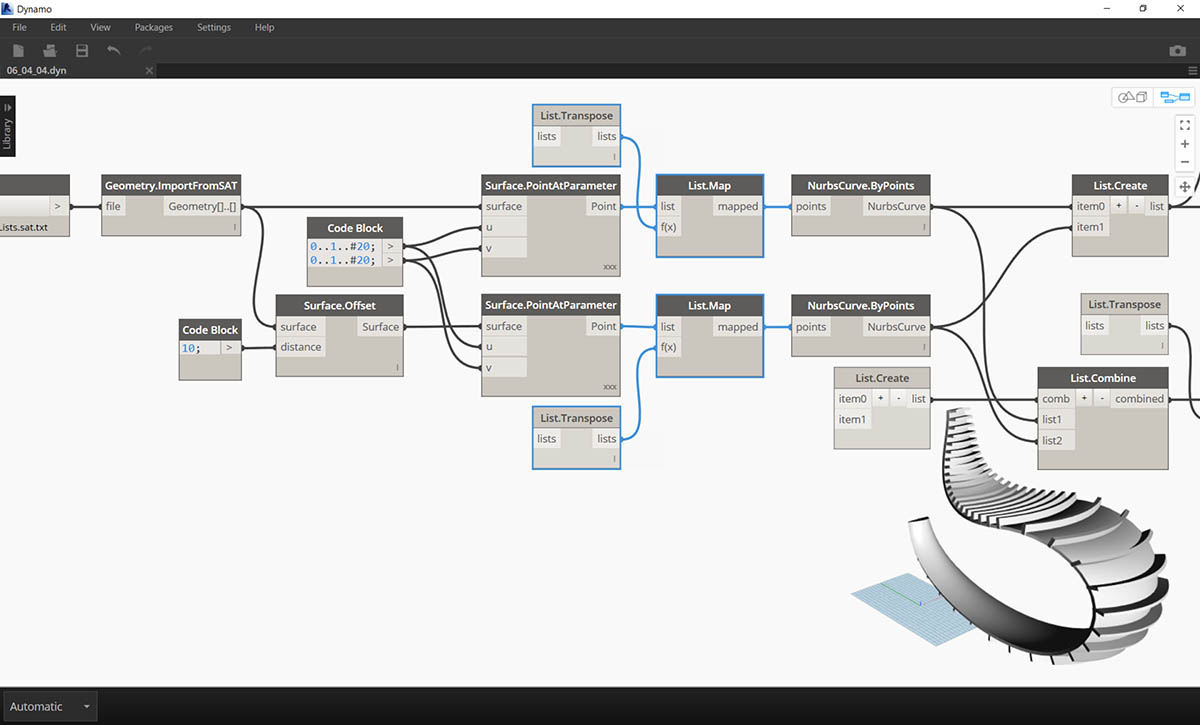
最后一步，我们反转带条纹成员的方向。如在上一练习中使用转置一样，我们将在此处执行类似操作。

1. 由于我们在层次结构中还有一层级，因此我们需要将 List.Map 与 List.Tranpose 函数一起使用来更改 NURBS 曲线的方向。

1. 我们可能希望增加踏板数，因此可以将代码块更改为

0..1..#20;
0..1..#10;

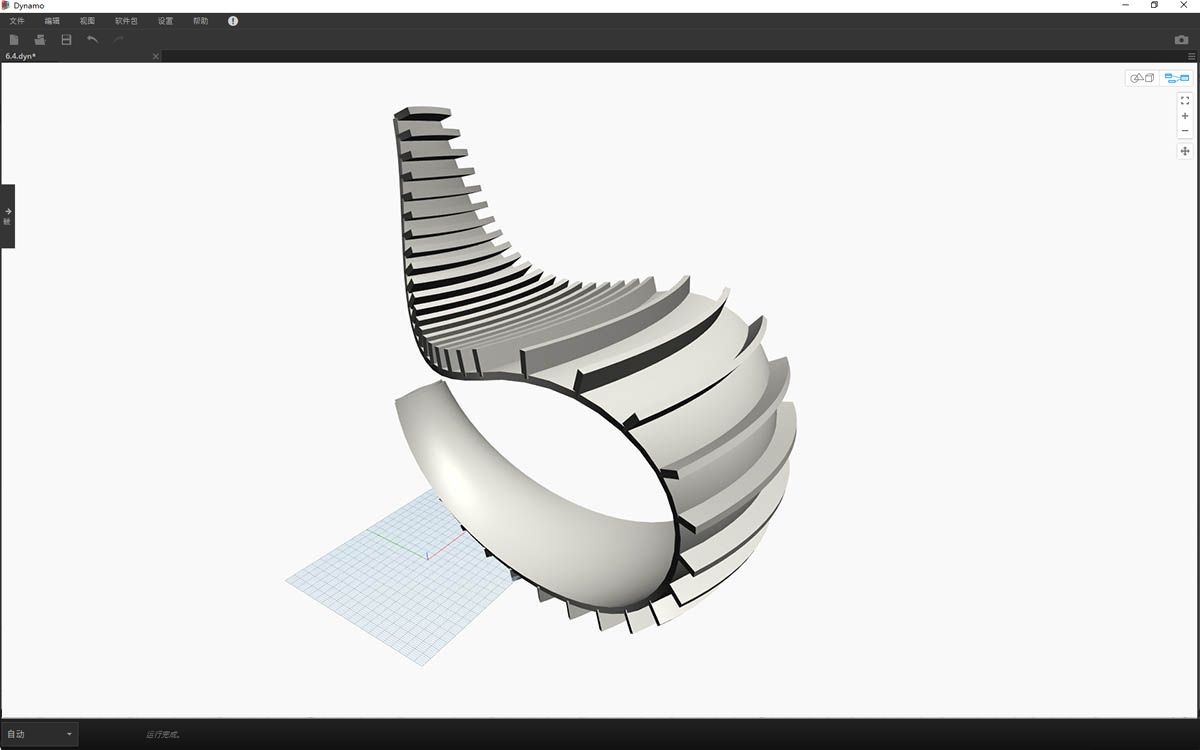
摇椅的第一个版本很流畅，因此我们的第二个模型提供了越野、运动多功能版本的靠背。