简单来说,代码块中有一些基本的简写方法,这些方法使数据管理更加容易。我们将详细介绍下面的基础知识,并讨论如何使用此简写来创建和查询数据。
| 数据类型 | 标准 Dynamo | 等效代码块 |
|---|---|---|
| 数字 | 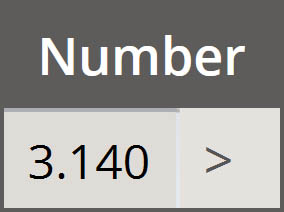 |
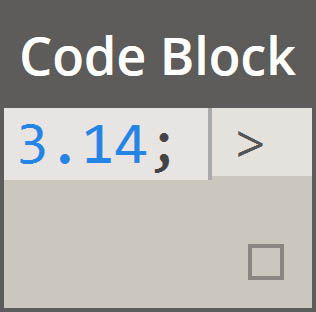 |
| 字符串 | 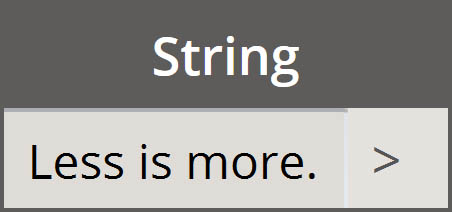 |
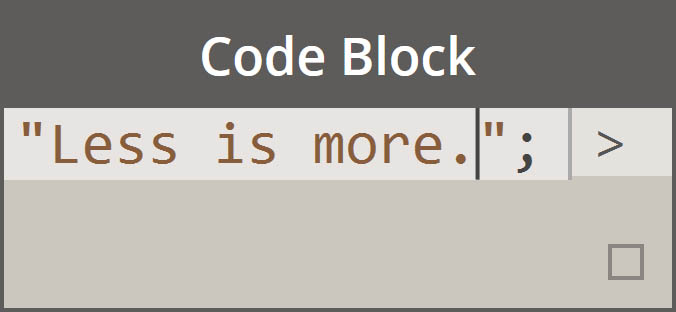 |
| 序列 | 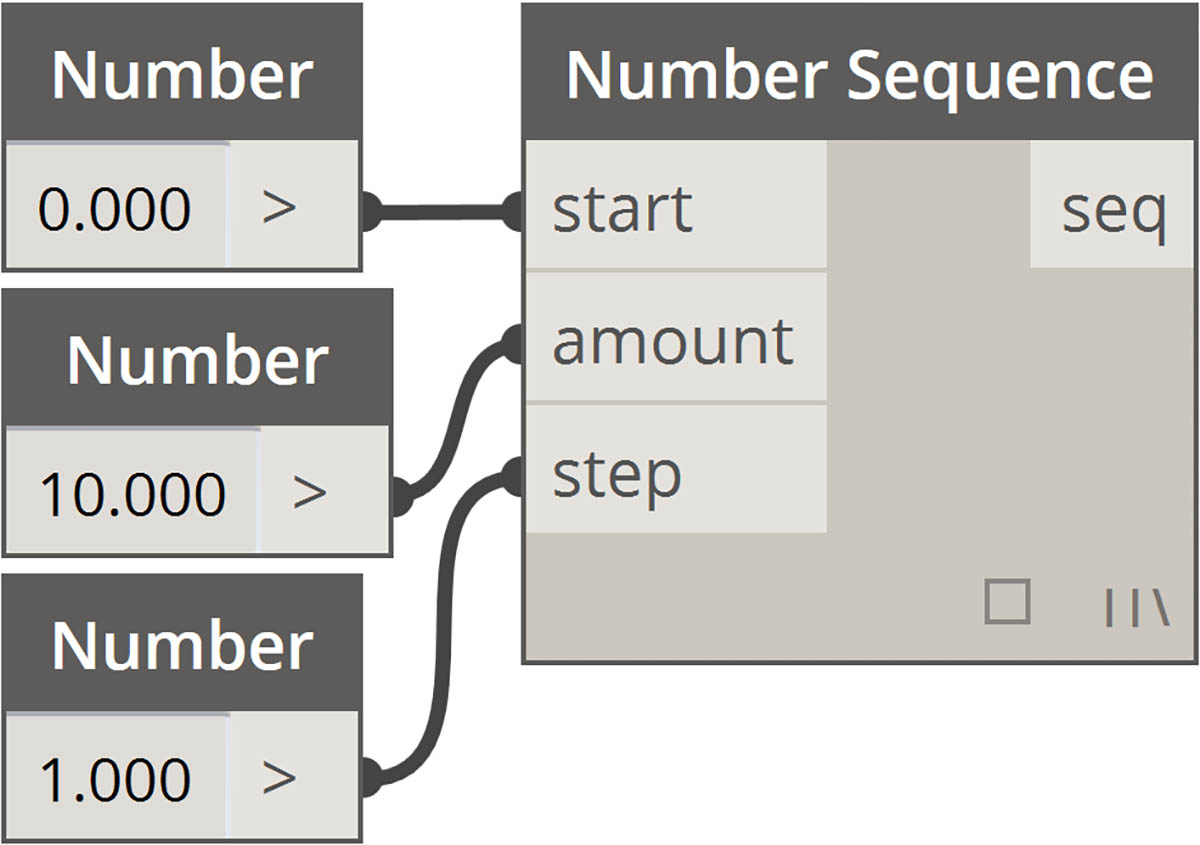 |
 |
| 范围 | 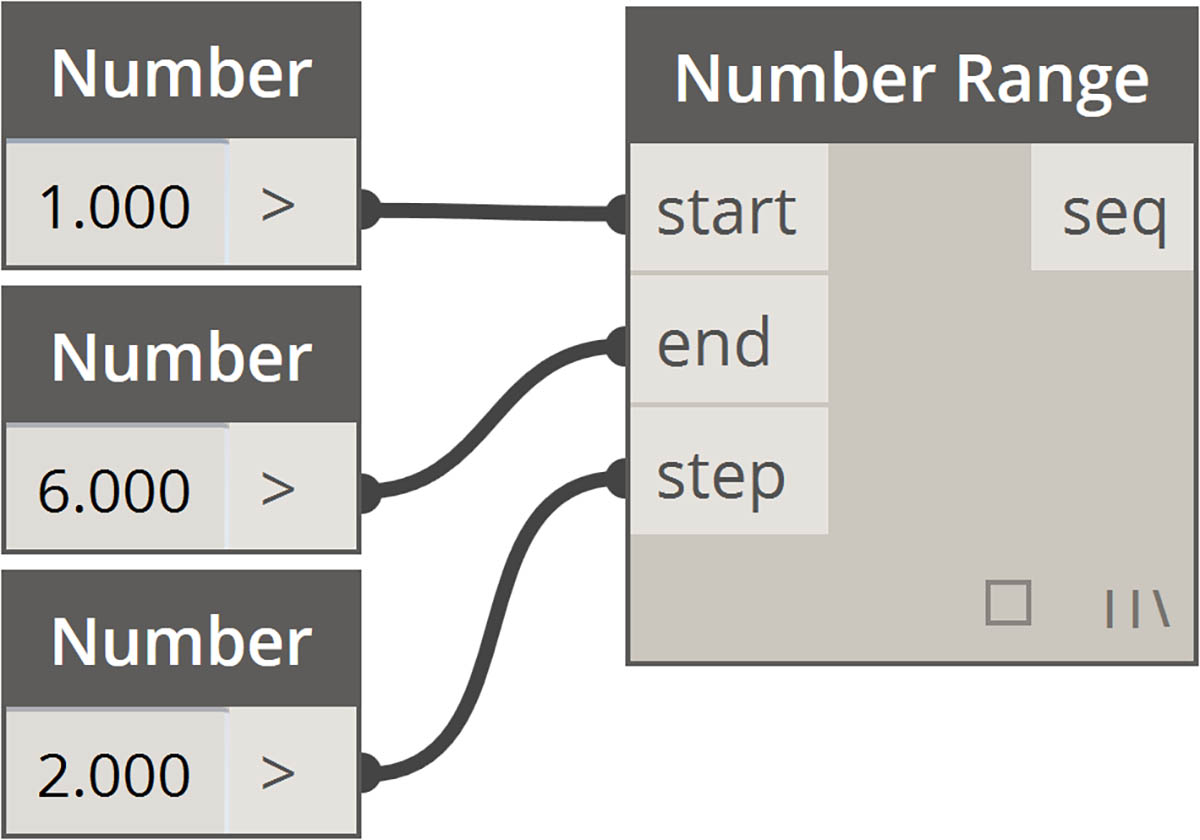 |
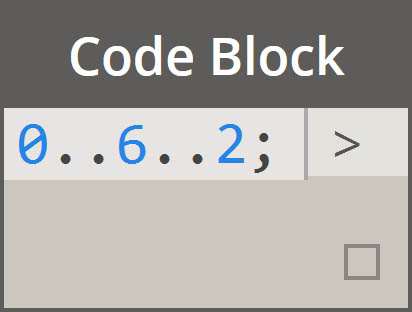 |
| 获取索引处的项目 | 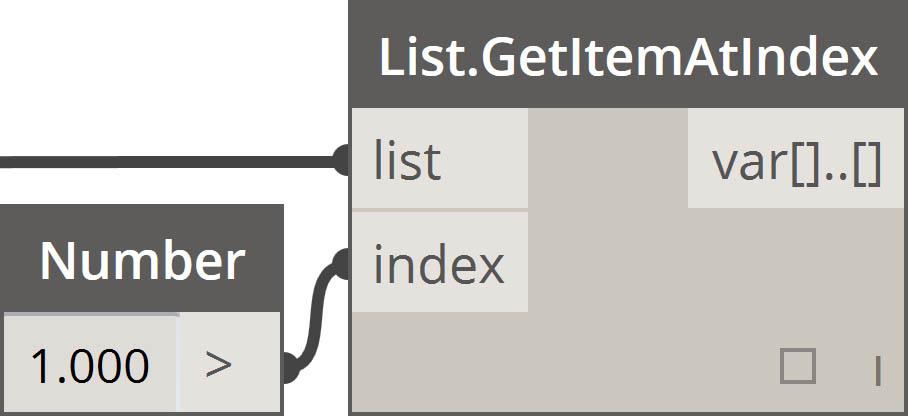 |
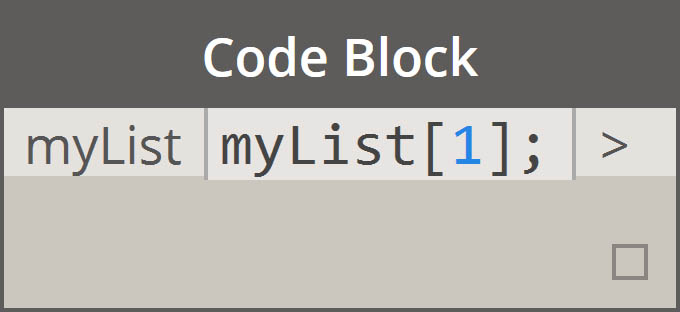 |
| 创建列表 | 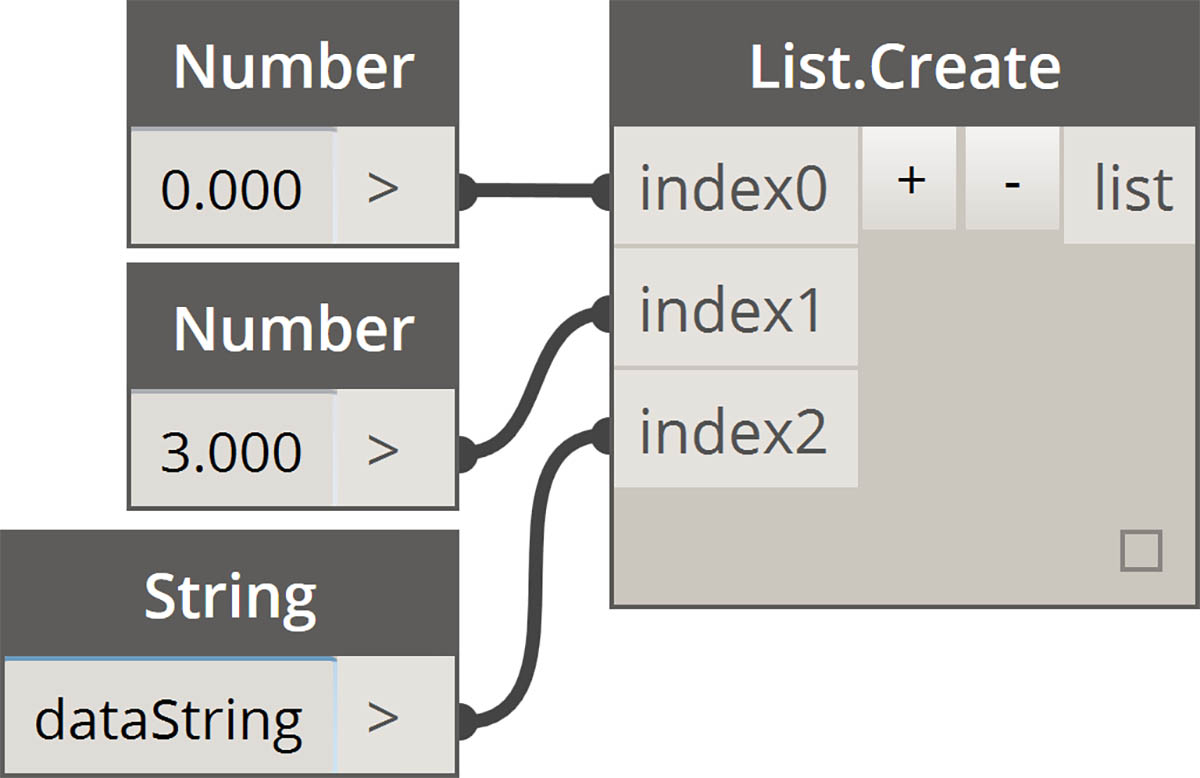 |
 |
| 连接字符串 | 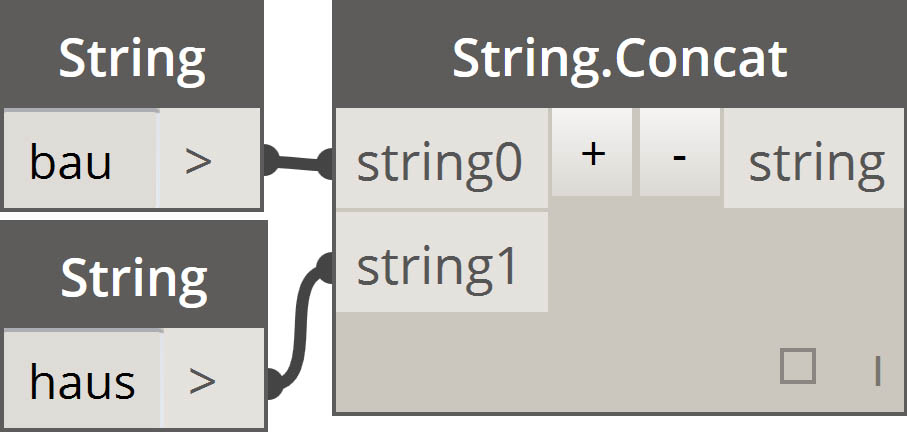 |
 |
| 条件语句 | 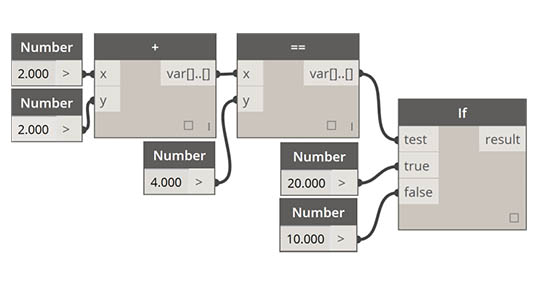 |
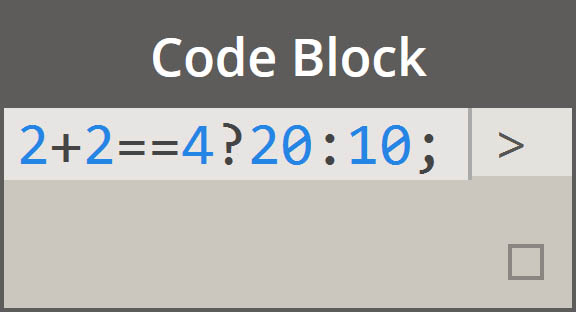 |
其他语法
| 节点 | 等效代码块 | 注释 |
|---|---|---|
| 任何运算符(+、&&、>=、Not 等) | +、&&、>=、! 等 | 请注意,“Not”变为“!”但该节点称为“Not”以区分“阶乘” |
| 布尔值 True | true; | 注意小写 |
| 布尔值 False | false; | 注意小写 |
范围
定义范围和序列的方法可缩减为基本简写。使用下图作为“..”语法的指导,以使用代码块定义数值数据列表。在完成此标记法后,创建数值数据是一个非常有效的过程: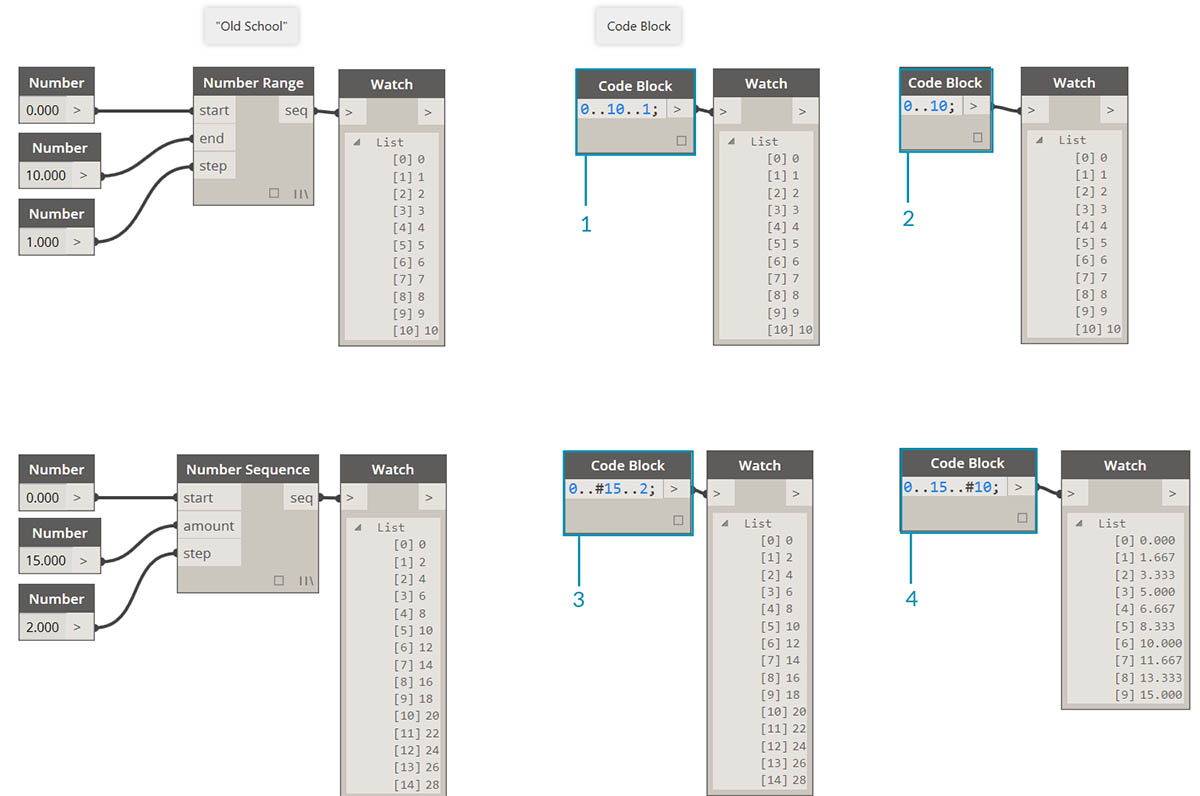
- 在此示例中,数字范围将替换为定义
beginning..end..step-size;的基本代码块语法。通过数字表示,可以得到:0..10..1;- 请注意,语法
0..10..1;等效于0..10;。步长 1 是简写符号的默认值。因此,0..10;将给出一个从 0 到 10 的序列(步长为 1)。- 数字序列示例类似,除了我们使用“#”来指明我们希望列表中包含 15 个值,而不是列表中的最大值为 15。在本例中,我们如下定义:
beginning..#ofSteps..step-size:。序列的实际语法为0..#15..2- 使用上一步中的“#”,现在将其放置在语法的“step-size”部分。现在,我们有一个数字范围,从“beginning”增长到“end”,“step-size”表示法指示在这两者之间均匀分布许多值:
beginning..end..#ofSteps
高级范围
创建高级范围后,我们即可简单地处理列表的列表。在下面的示例中,我们将隔离主要范围表示法的变量,并创建该列表的另一个范围。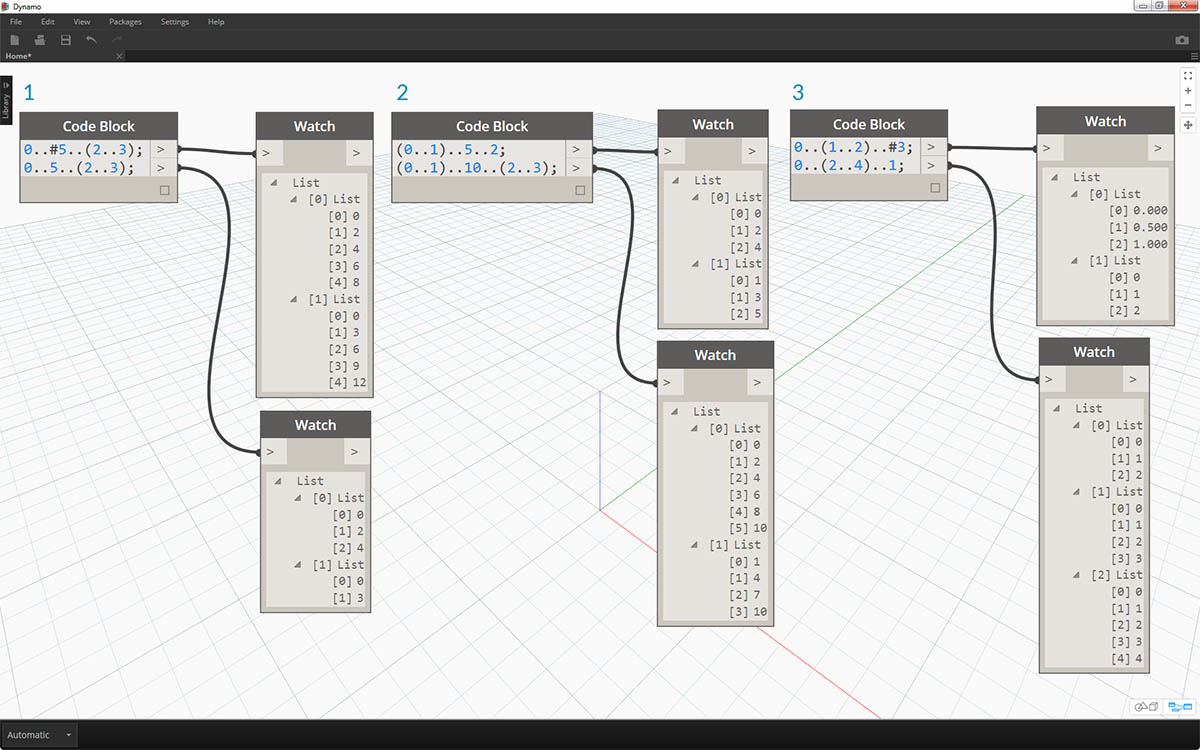
- 创建嵌套范围,将带“#”的表示法与不带符号的表示法进行比较。相同逻辑在基本范围中都适用,但它稍显复杂。
- 我们可以在主范围内的任意位置处定义子范围,请注意,我们也可以有两个子范围。
- 通过控制范围中的“end”值,我们可以创建长度不同的更多范围。
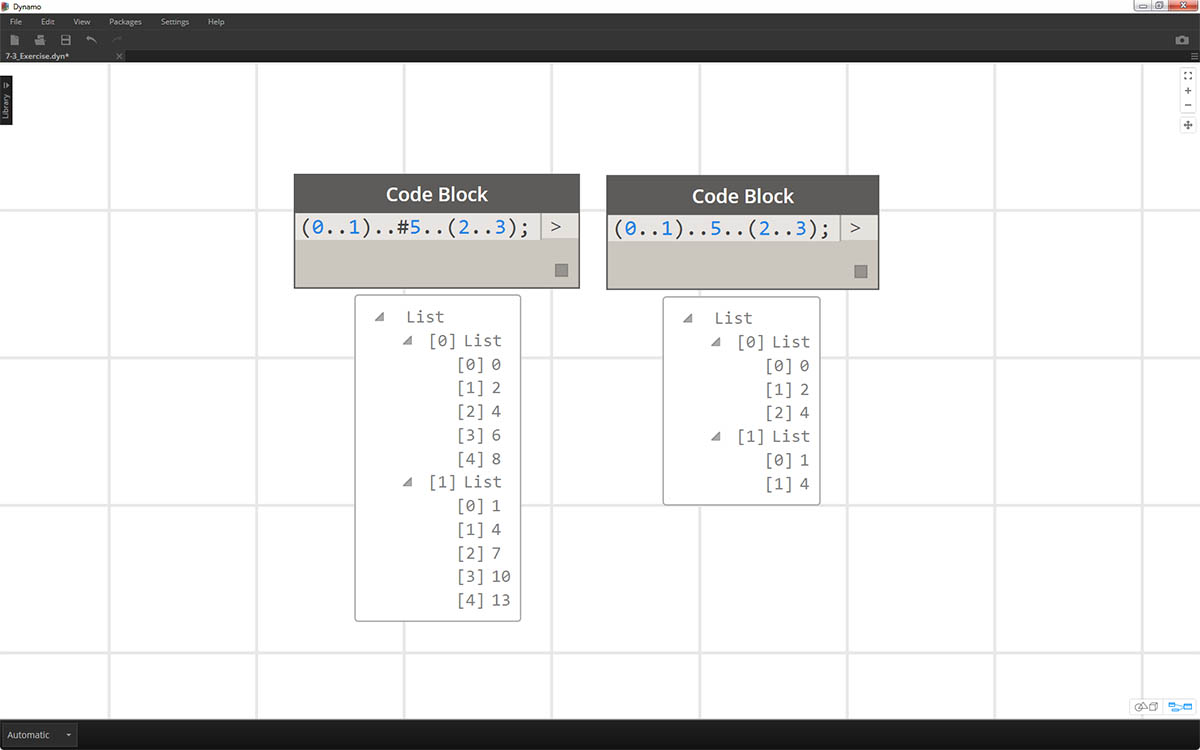
作为逻辑练习,请比较上述两个简写,并尝试解析 subranges 和“#”表示法如何驱动结果输出。
生成列表并从列表中获取项目
除了使用简写生成列表外,我们还可以即时创建列表。这些列表可以包含多种元素类型,也可以进行查询(请记住,列表本身就是对象)。总之,在使用代码块的情况下,可以创建带大括号的列表(也称为“波形括号”),并从带括号(即“方括号”)的列表中查询项目: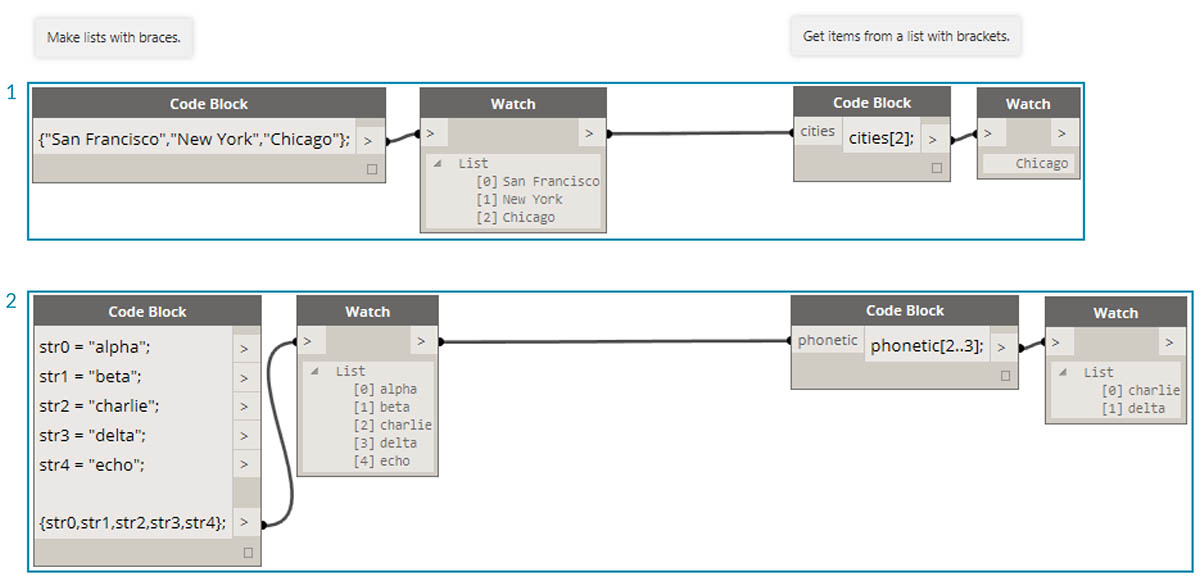
- 使用字符串快速创建列表,并使用项目索引进行查询。
- 使用变量创建列表,并使用范围简写表示法进行查询。
管理嵌套列表的过程类似。请注意列表顺序,并使用多组方括号进行调用: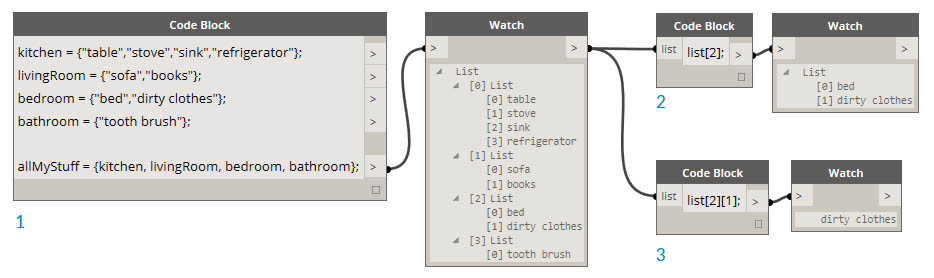
- 定义一列列表。
- 使用单括号表示法查询列表。
- 使用双括号表示法查询项目。
练习
下载本练习随附的示例文件(单击鼠标右键,然后单击“将链接另存为…”)。 Obsolete-Nodes_Sine-Surface.dyn
在本练习中,我们将调整新的简写技能,以创建由范围和公式定义的精美蛋壳曲面。在本练习中,请注意我们如何串联使用代码块和现有 Dynamo 节点:我们将代码块用于繁重的数据提升,而 Dynamo 节点以可视方式布局来使定义清晰易读。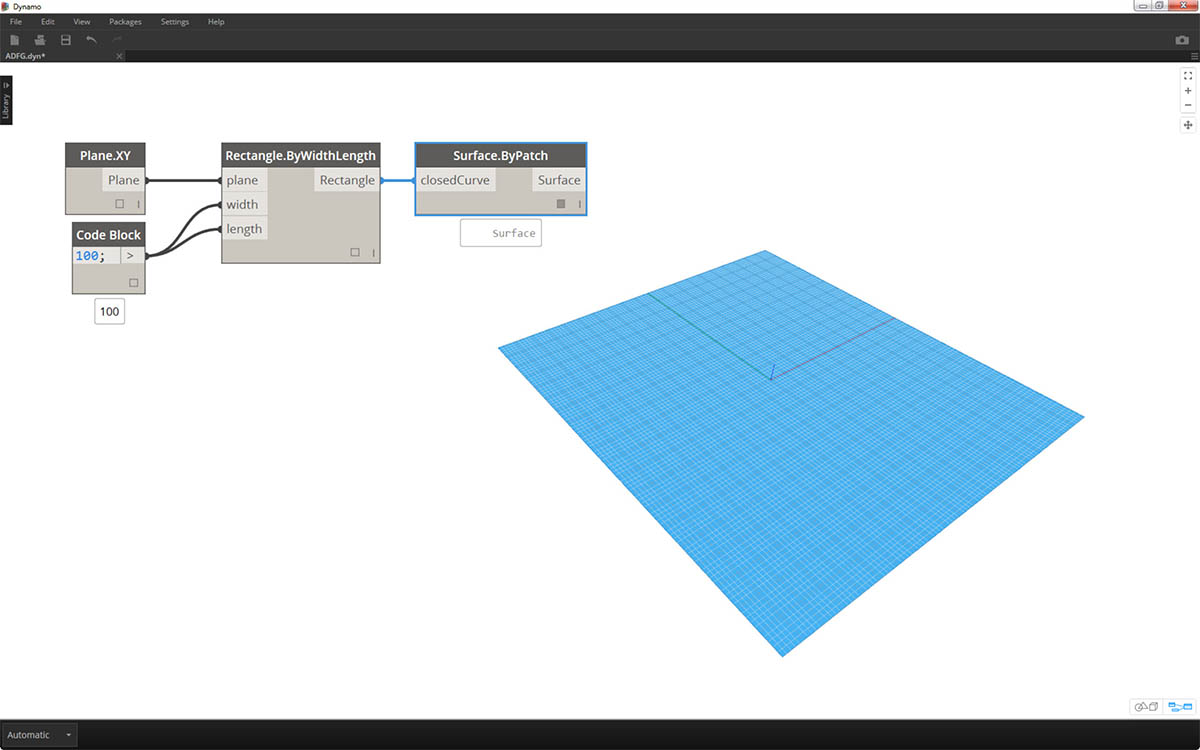
首先,通过连接上述节点创建曲面。请勿使用数字节点定义宽度和长度,只需双击画布,然后在代码块中键入
100;。
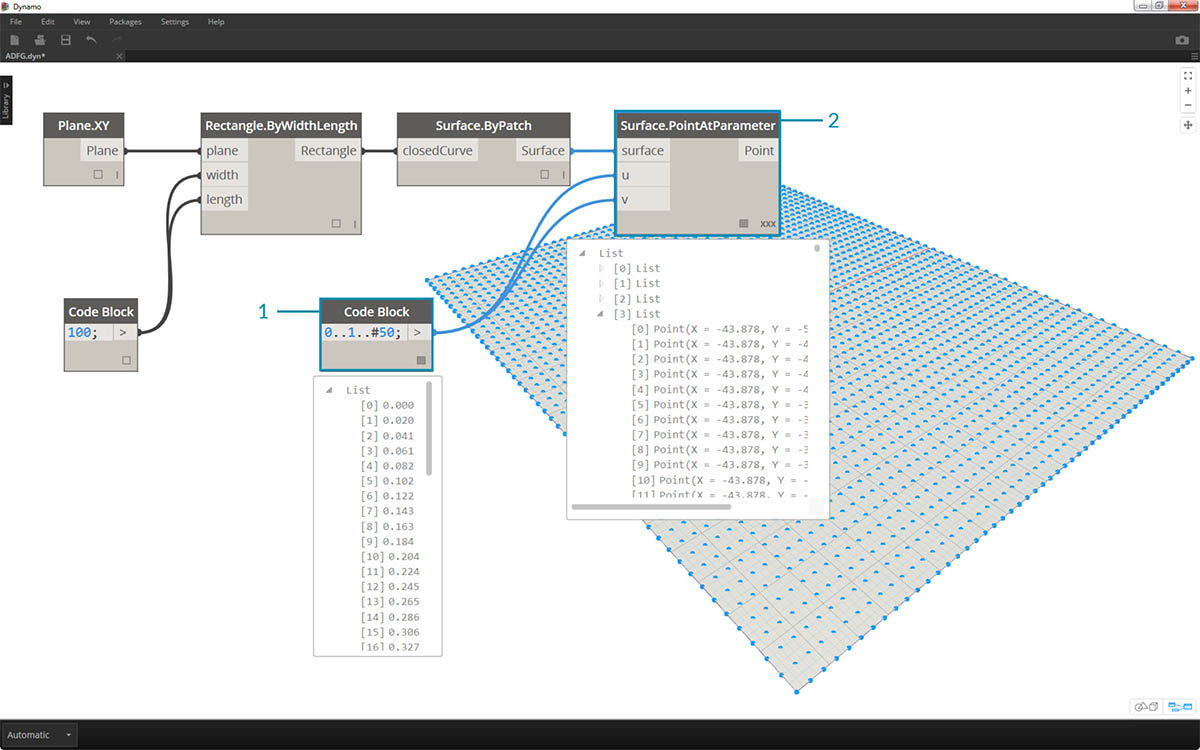
- 通过在代码块中键入
0..1..#50,定义一个介于 0 和 1 之间的范围(其中包含 50 个划分)。- 将该范围连接到 Surface.PointAtParameter,该范围在曲面上提取介于 0 和 1 之间的 u 和 v 值。请记得通过在 Surface.PointAtParameter 节点上单击鼠标右键,将“连缀”更改为“叉积”。
在此步骤中,我们将使用第一个函数以在 Z 方向上上移动点栅格。此栅格将基于底层函数驱动生成的曲面。
- 将可视节点添加到画布,如上图中所示。
- 我们不使用公式节点,而是使用含有以下代码行的代码块:
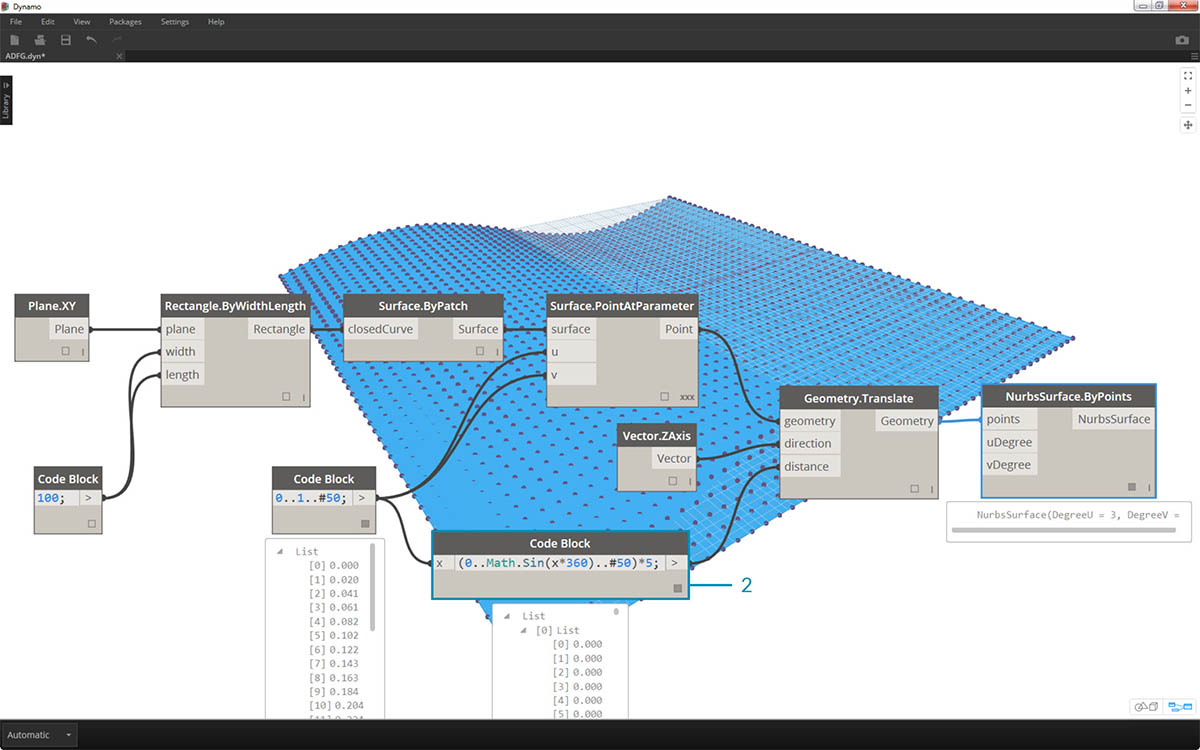
(0..Math.Sin(x*360)..#50)*5;。为了对此快速详细介绍,我们定义了一个内部带有公式的范围。此公式为正弦函数。在 Dynamo 中,正弦函数接收度数输入,因此为了获得完整正弦波,我们将x 值(这一范围输入介于 0 到 1 之间)乘以 360。接下来,我们希望每行都具有与控制栅格点相同数量的划分,因此我们用 #50 定义了 50 个细分。最后,乘数 5 只会增加平移幅度,因此我们可以在 Dynamo 预览中查看效果。
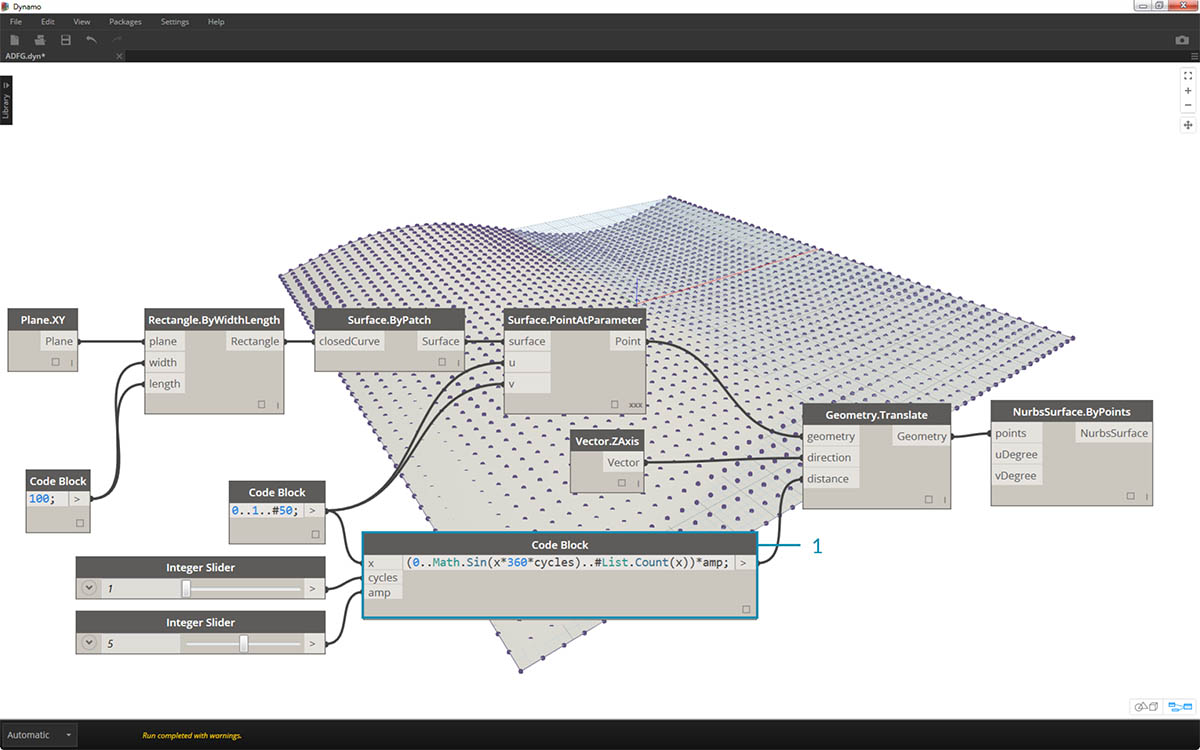
- 虽然上一个代码块正常工作,但它并非完全参数化。我们希望动态驱动其参数,因此我们将上一步中的代码行替换为
(0..Math.Sin(x*360*cycles)..#List.Count(x))*amp;。这使我们可以根据输入定义这些值。
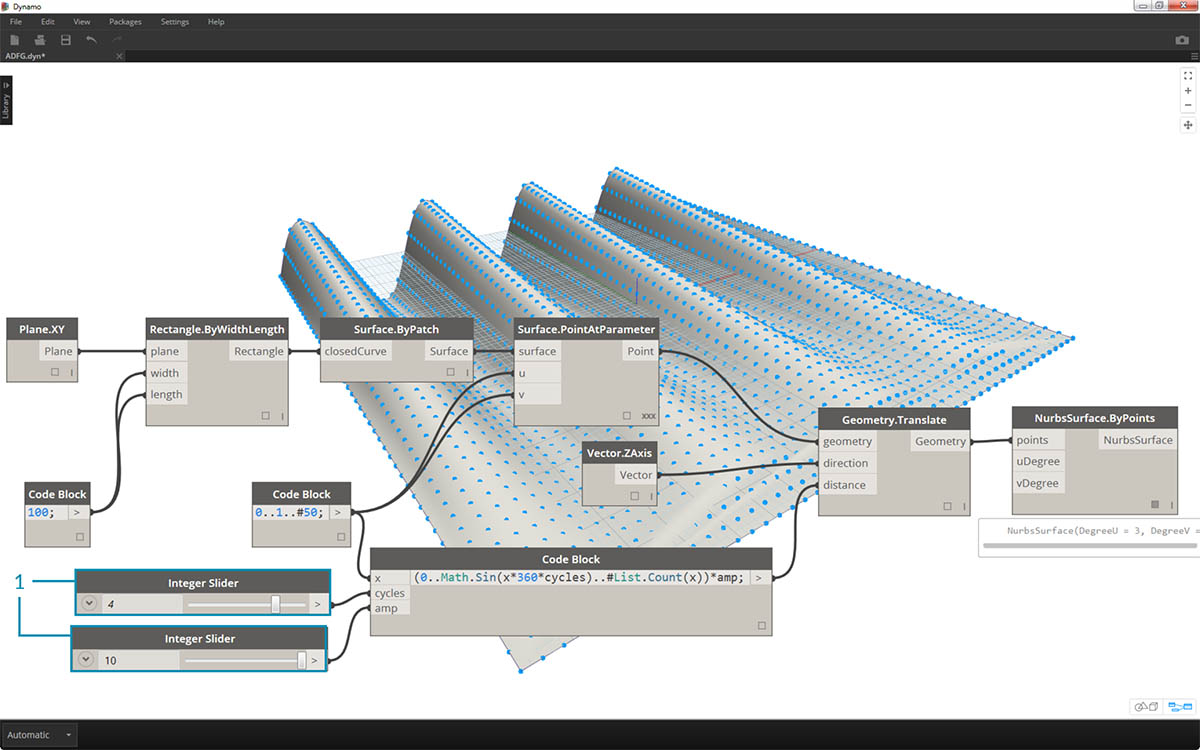
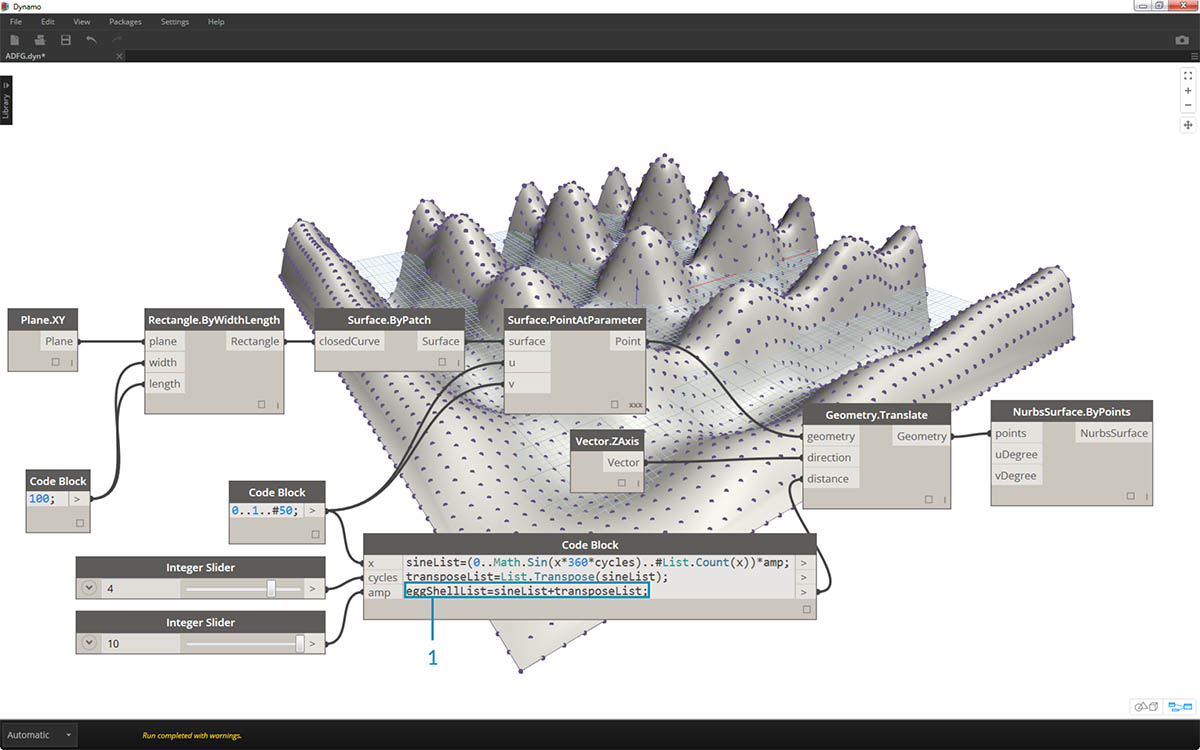
- 通过更改滑块(范围介于 0 到 10 之间),我们得到了一些有趣的结果。
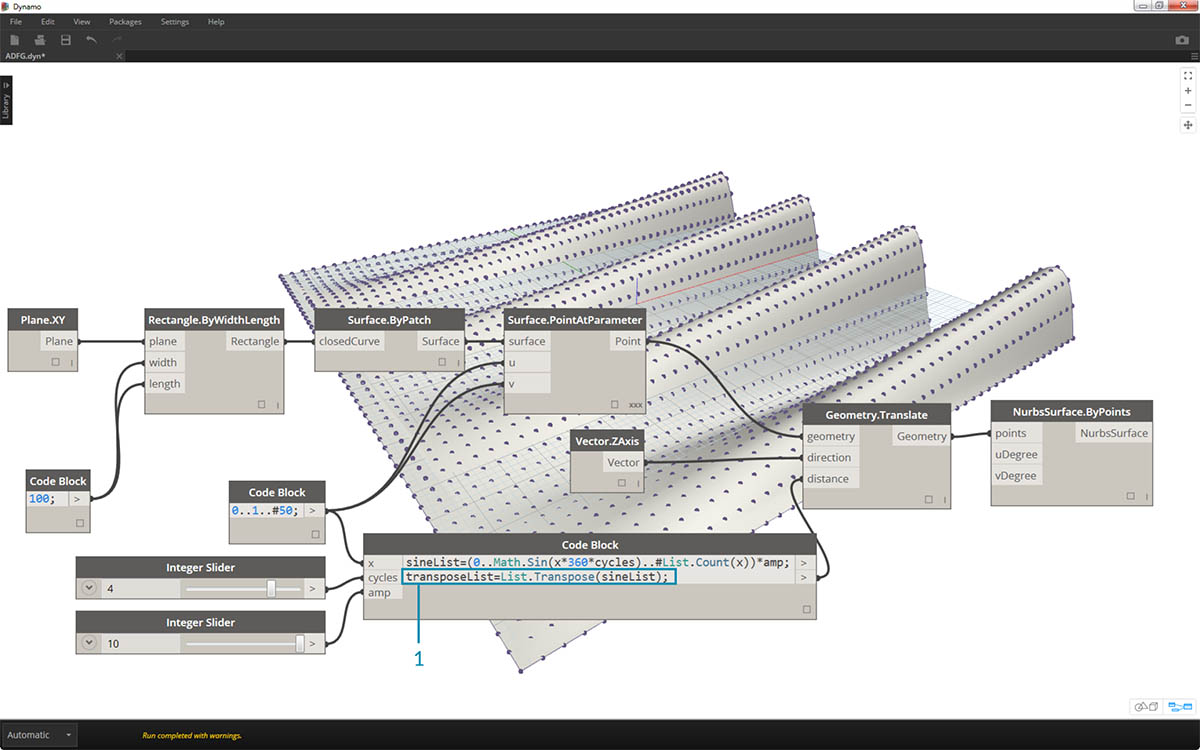
- 通过对数字范围执行转置,我们可以反转幕墙波的方向:
transposeList = List.Transpose(sineList);
- 如果添加 sineList 和 tranposeList,我们会得到一个扭曲的蛋壳曲面:
eggShellList = sineList+transposeList;
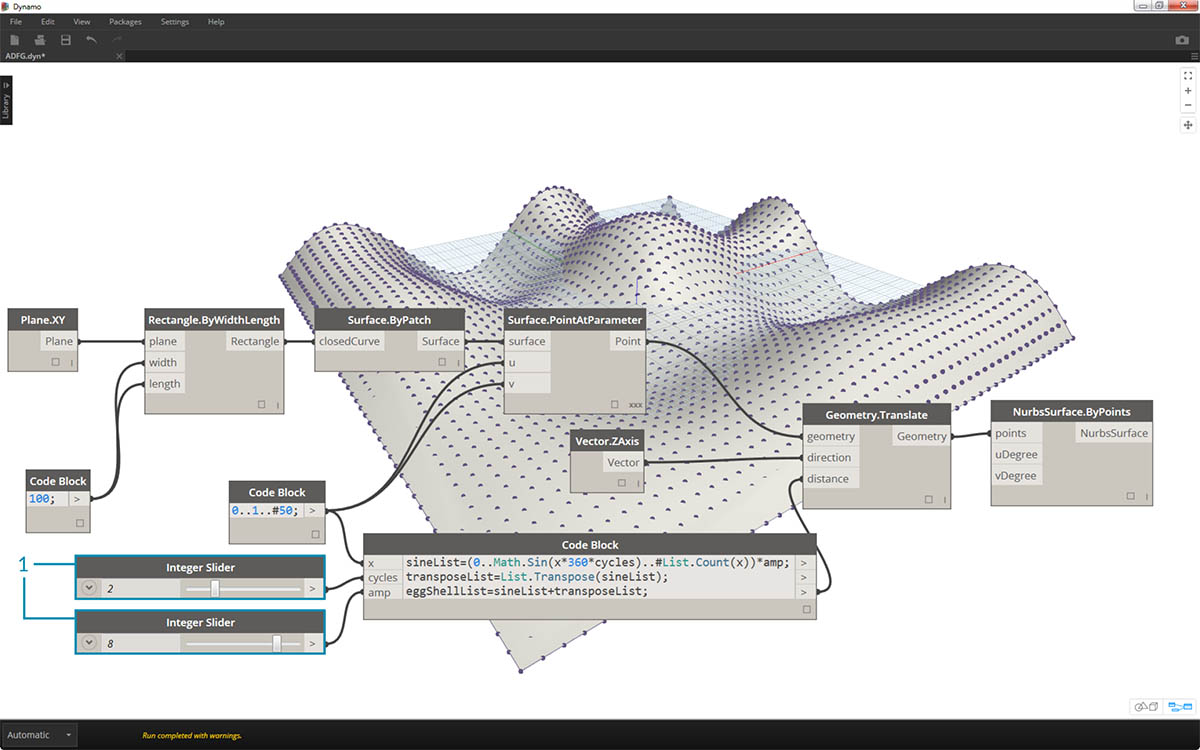
- 再次更改滑块,可以让我们平静地控制此算法的范围。
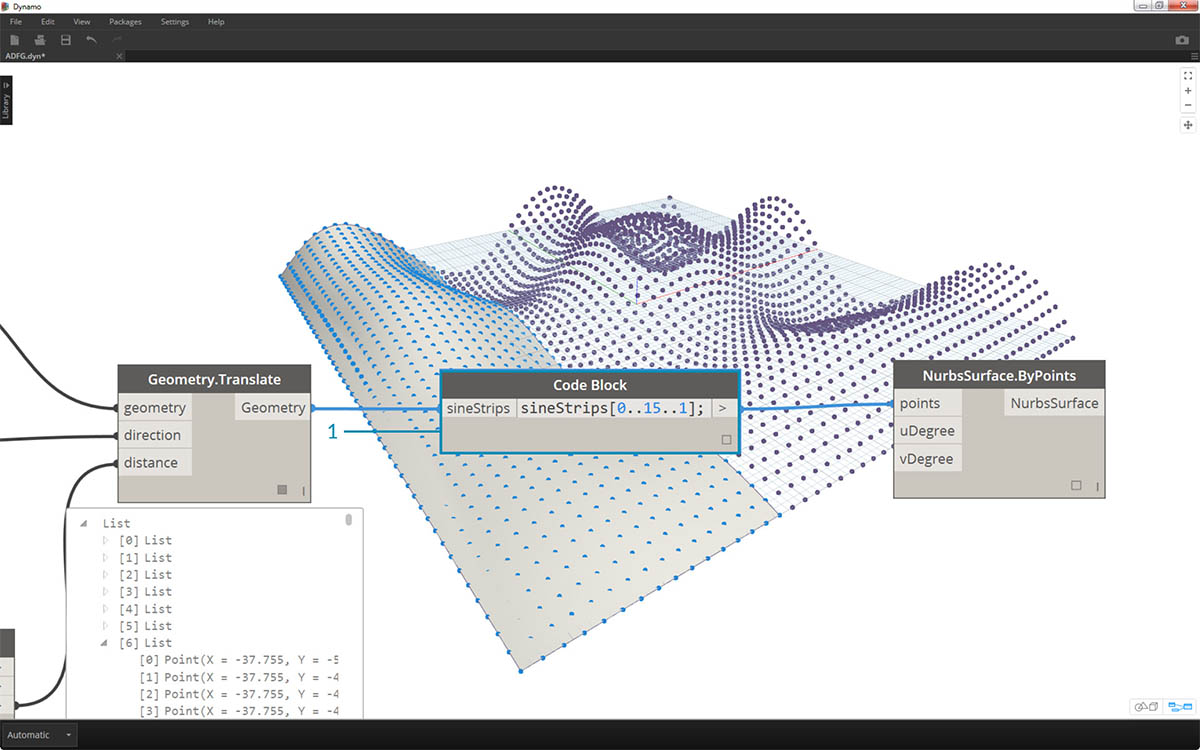
- 最后,让我们使用代码块查询数据的隔离部分。要使用特定范围的点重新生成曲面,请在 Geometry.Translate 和 NurbsSurface.ByPoints 节点之间添加上述代码块。这有以下文本行:
sineStrips[0..15..1];。这将选择前 16 行点(共 50 行)。通过重新创建曲面,可以查看我们生成了点栅格的隔离部分。

- 在最后一步中,为了提高此代码块的参数化,我们使用介于 0 到 1 之间的滑块来驱动查询。我们使用以下代码行来执行此操作:
sineStrips[0..((List.Count(sineStrips)-1)*u)];。这看起来可能会令人困惑,但代码行提供的方法让我们可以快速地将列表的长度缩放为 0 到 1 之间的乘数。
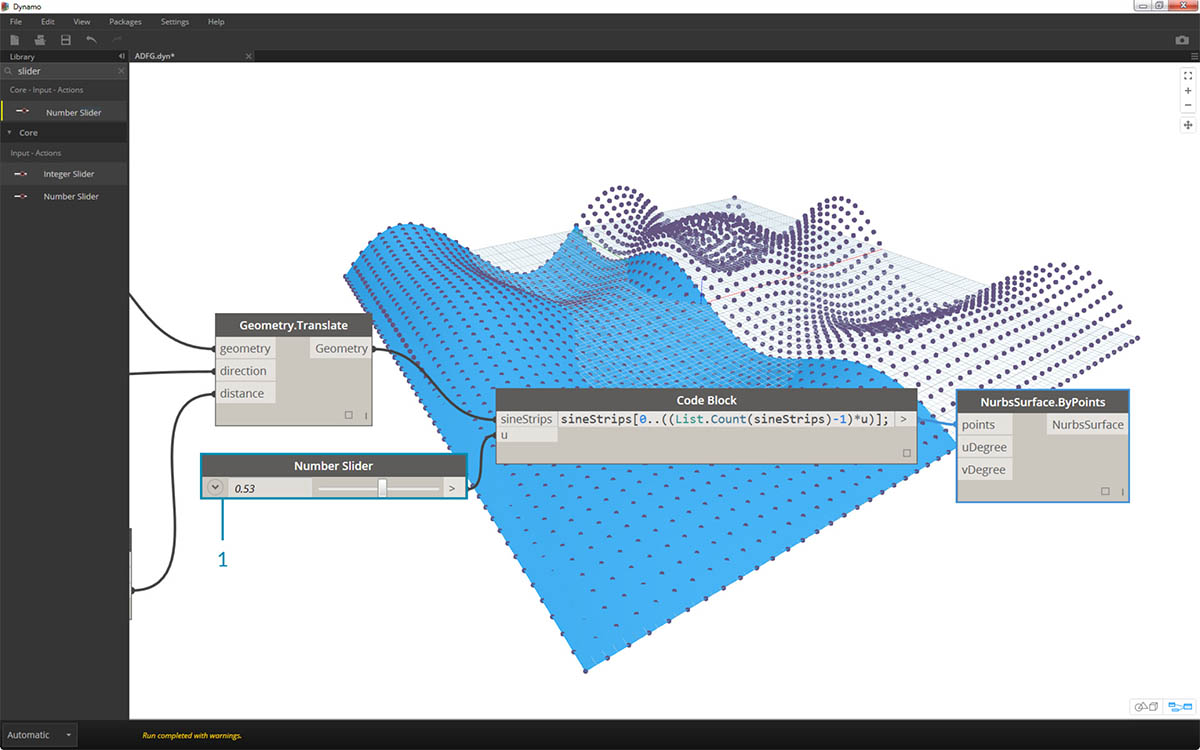
- 滑块上的值 .53 可创建刚好经过栅格中点的曲面。
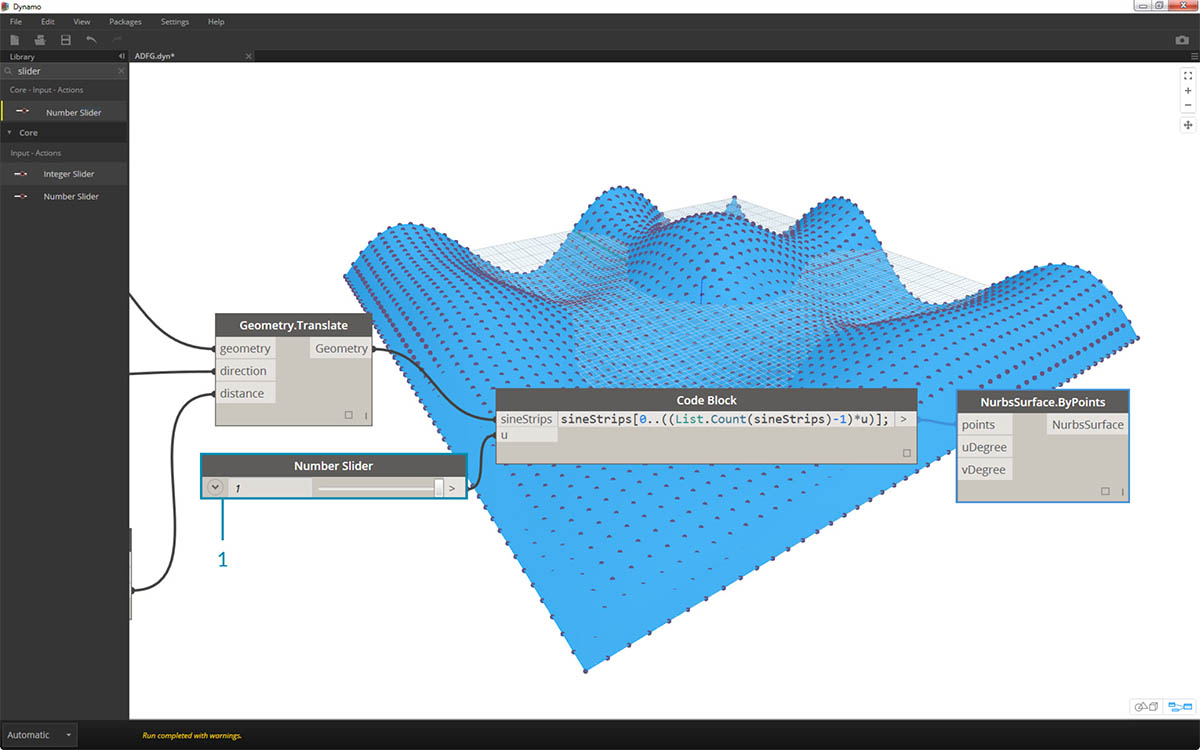
- 如预期的一样,值为 1 的滑块会基于完整的栅格点创建曲面。
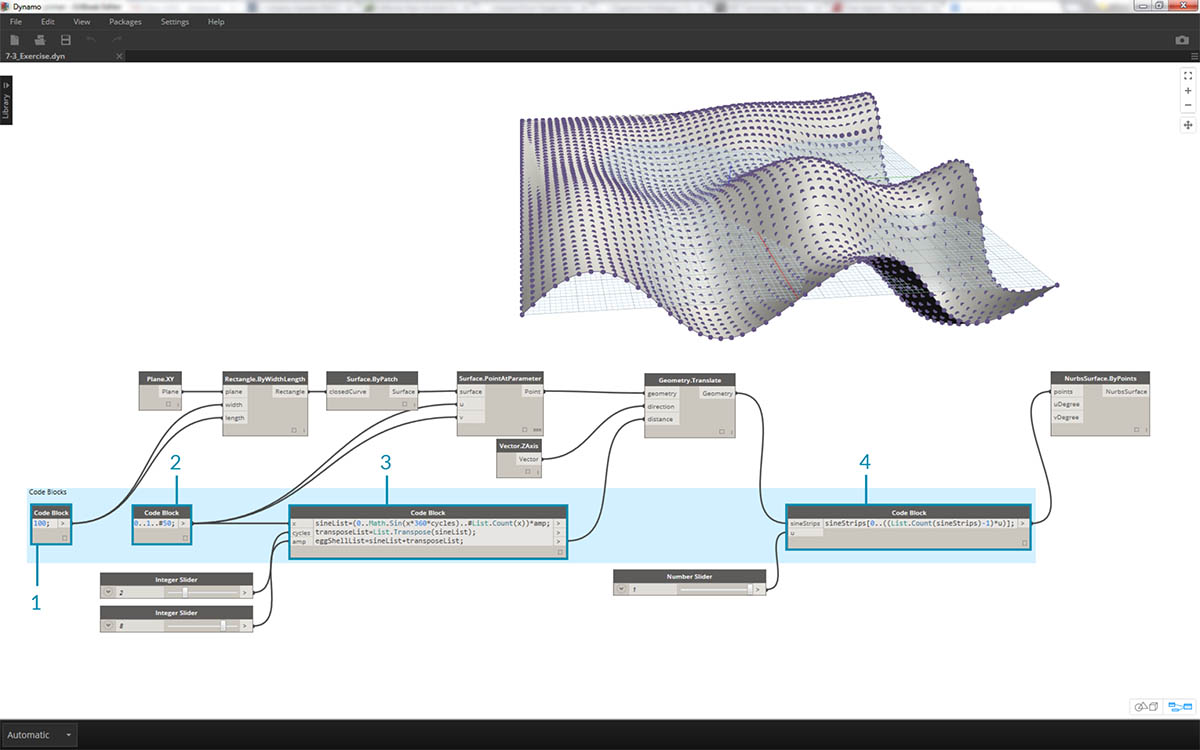
查看生成的可视图形,我们可以亮显代码块并查看其每个函数。
- 第一个代码块替换 Number 节点。
- 第二个代码块替换了 Number Range 节点。
- 第三个代码块替换 Formula 节点(以及 List.Transpose、List.Count 和 Number Range)。
- 第四个代码块查询一列列表,以便替换 List.GetItemAtIndex 节点。

