4.2 数学

如果最简单的数据形式是数字，则将这些数字关联起来的最简单方法是通过数学。从除法等简单的运算符到三角函数，再到更复杂的公式，Math 是开始探索数值关系和模式的好方法。

算术运算符

运算符是一组组件，这些组件使用具有两个数字输入值的代数函数，这些结果产生一个输出值（加、减、乘、除等）。这些可在“运算符”>“操作”下找到。

图标	名称	语法	输入(Inputs)	输出
	添加	+	var[]…[], var[]…[]	var[]…[]
	相减(Subtract)	-	var[]…[], var[]…[]	var[]…[]
	相乘(Multiply)	*	var[]…[], var[]…[]	var[]…[]
	分割	/	var[]…[], var[]…[]	var[]…[]

参数化公式

下载本练习随附的示例文件（单击鼠标右键，然后单击“将链接另存为…”）： 构建程序块 - Math.dyn

通过运算符，下一个逻辑步骤是通过公式组合运算符和变量以形成更复杂的关系。让我们创建一个可由输入参数（如滑块）控制的公式。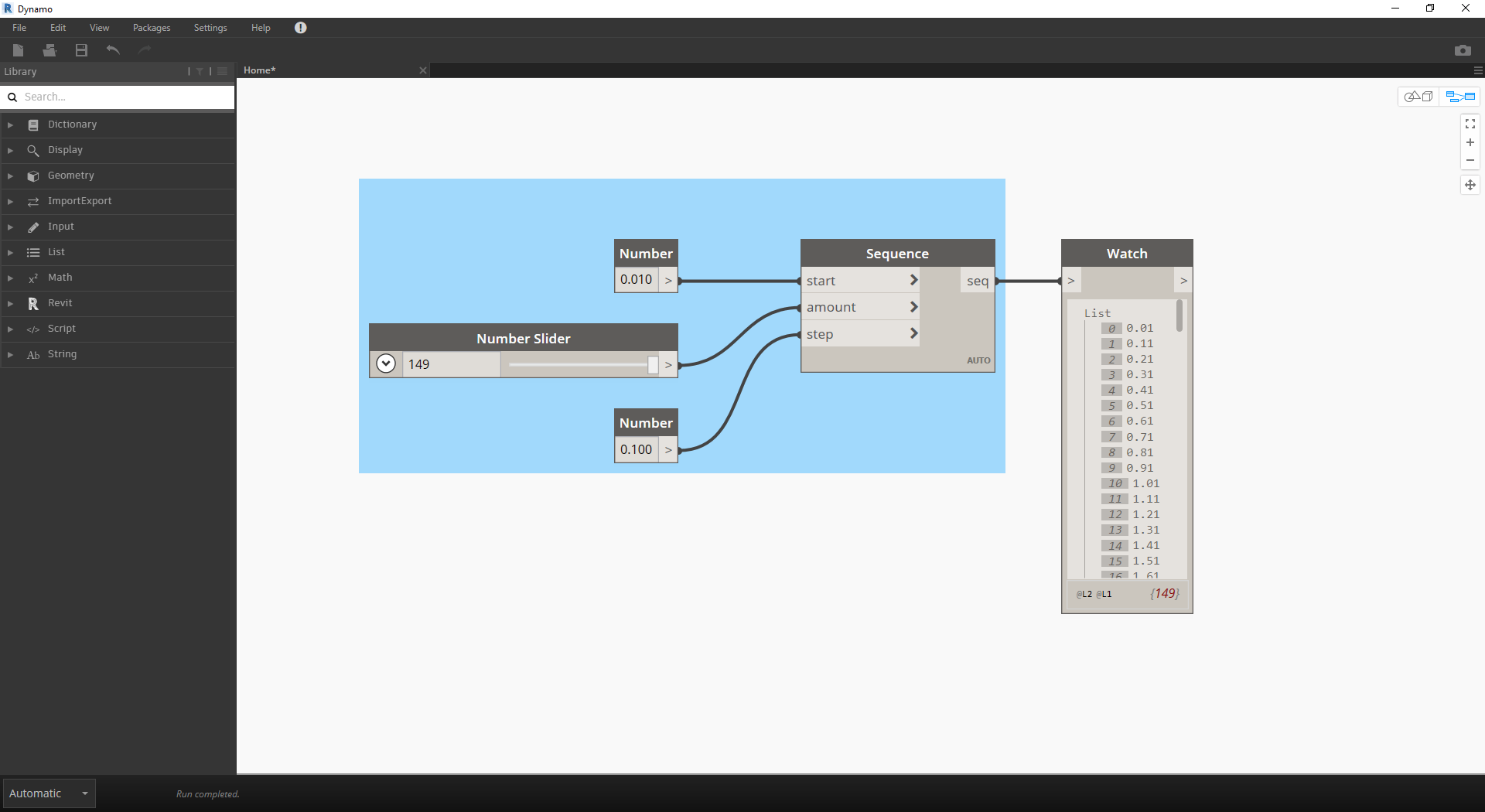

1. Number Sequence：基于以下三个输入定义数字序列：start、amount 和 step。此序列表示参数方程中的“t”，因此我们要使用足够大的列表来定义螺旋。

上述步骤已创建一列数字，来定义参数化域。金螺旋定义为以下方程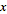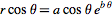：= 和 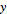=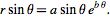。下面的节点组以可视化编程形式表示此方程。

在逐步查看节点组时，请尝试注意可视程序和编写方程之间的平行性。

1. Number Slider：向画布添加两个数字滑块。这些滑块将表示参数方程的 a 和 b 变量。这些表示灵活的常量，或我们可以根据所需结果调整的参数。
2. *：乘法节点由星号表示。我们将反复使用它来连接乘法变量
3. Math.RadiansToDegrees：“t”值需要转换为度数，以便在三角函数中进行求值。请记住，Dynamo 默认使用度数来对这些函数求值。
4. Math.Pow：作为“t”和数字“e”的函数，这将创建 Fibonacci 数列。
5. Math.Cos 和 Math.Sin：这两个三角函数将分别区分每个参数点的 x 坐标和 y 坐标。
6. Watch：现在，我们看到输出为两个列表，它们将是用于生成螺旋的点的 x 和 y 坐标。

从公式到几何图形

现在，上一步中的大部分节点都可以正常工作，但这种工作量很大。要创建更高效的工作流，请查看“代码块”（第 3.3.2.3 节），将 Dynamo 表达式的字符串定义到一个节点中。在接下来的一系列步骤中，我们将了解如何使用参数方程绘制 Fibonacci 螺旋。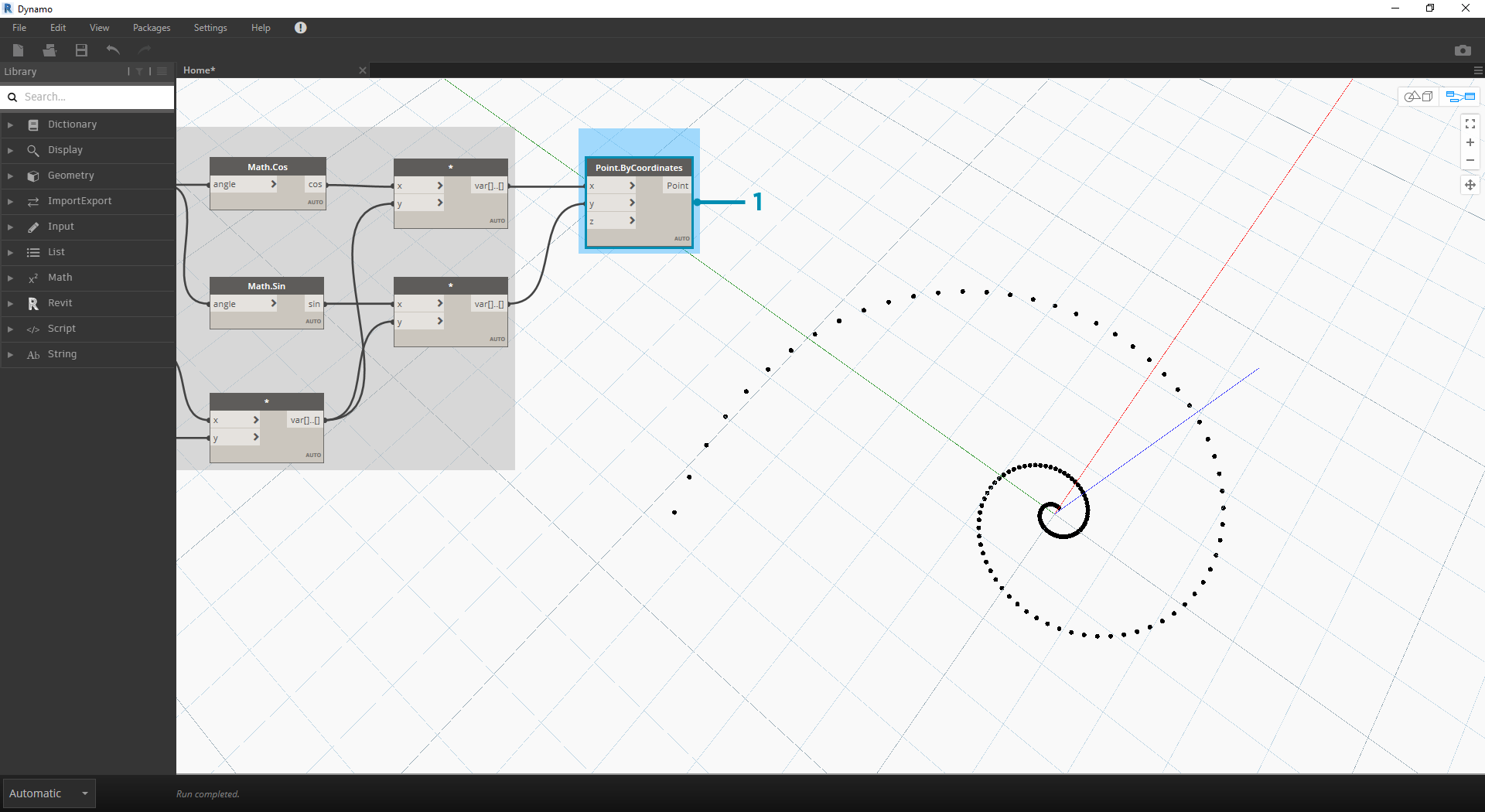

1. Point.ByCoordinates：将上乘法节点连接到 x 输入，将下乘法节点连接到 y 输入。现在，我们在屏幕上会看到点的参数化螺旋。

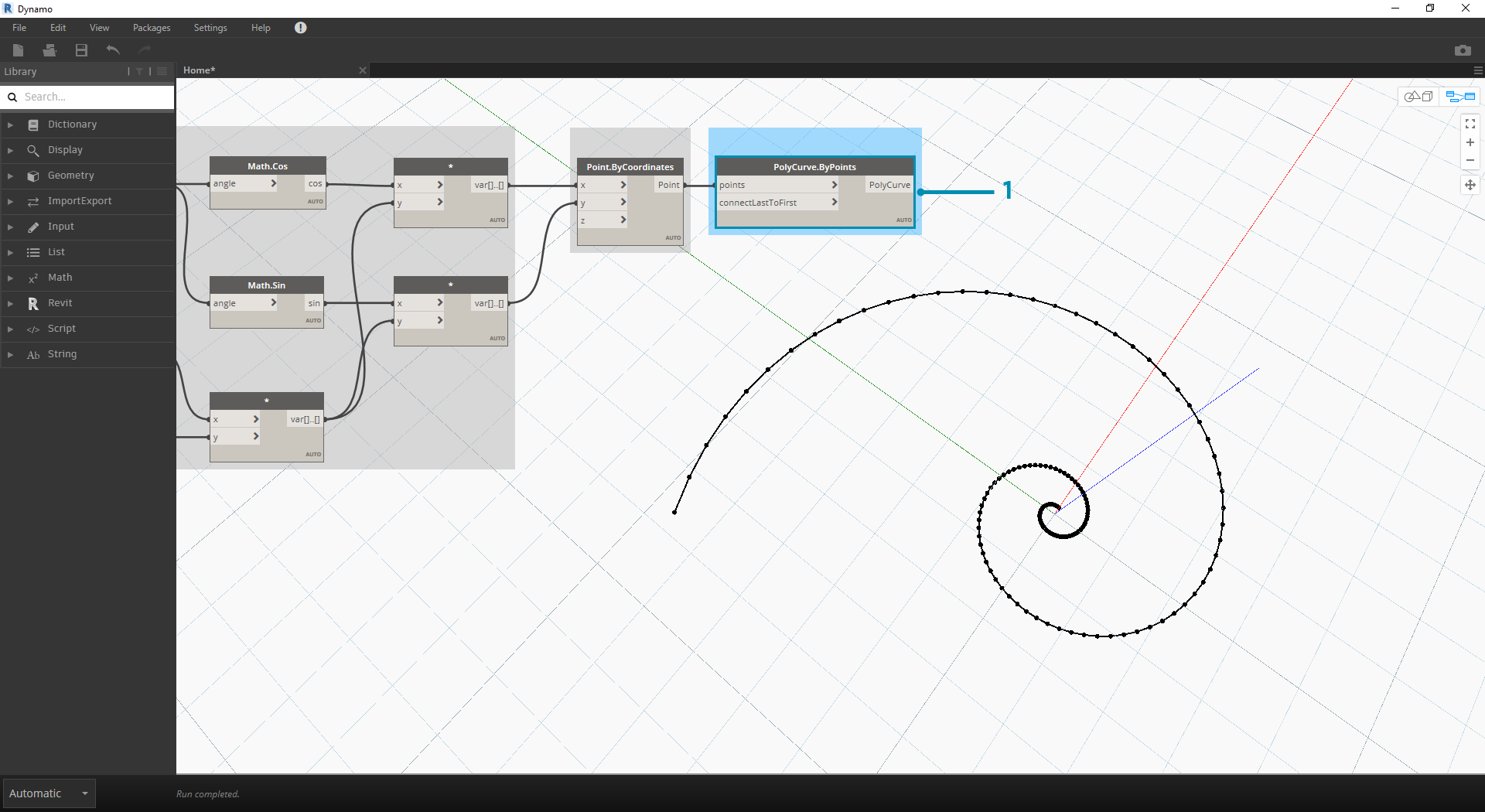
1. Polycurve.ByPoints：将上一步的 Point.ByCoordinates 连接到 points。我们可以不输入而保留 connectLastToFirst，因为我们不会绘制闭合曲线。这将创建穿过上一步中定义的每个点的螺旋。

我们现在已完成 Fibonacci 螺旋！让我们从此处开始进一步研究两个独立的练习，我们称之为 Nautilus 和 Sunflower。这些是自然系统的抽象表示，但 Fibonacci 螺旋的两种不同应用将得到充分体现。

从螺旋到 Nautilus

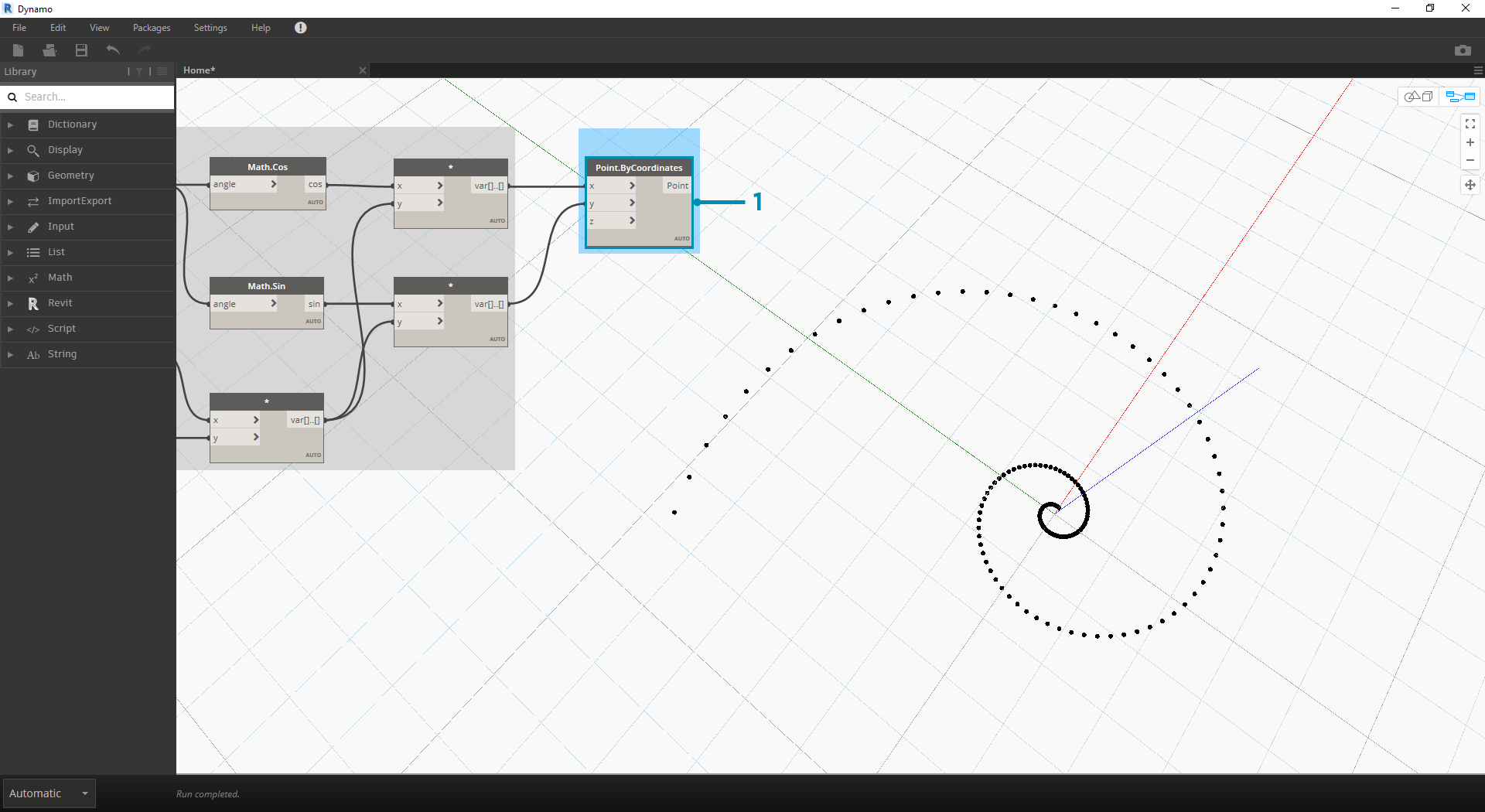
1. 作为一个跳跃点，我们从上一练习的相同步骤开始：使用 Point.ByCoordinates 节点创建点的螺旋阵列。

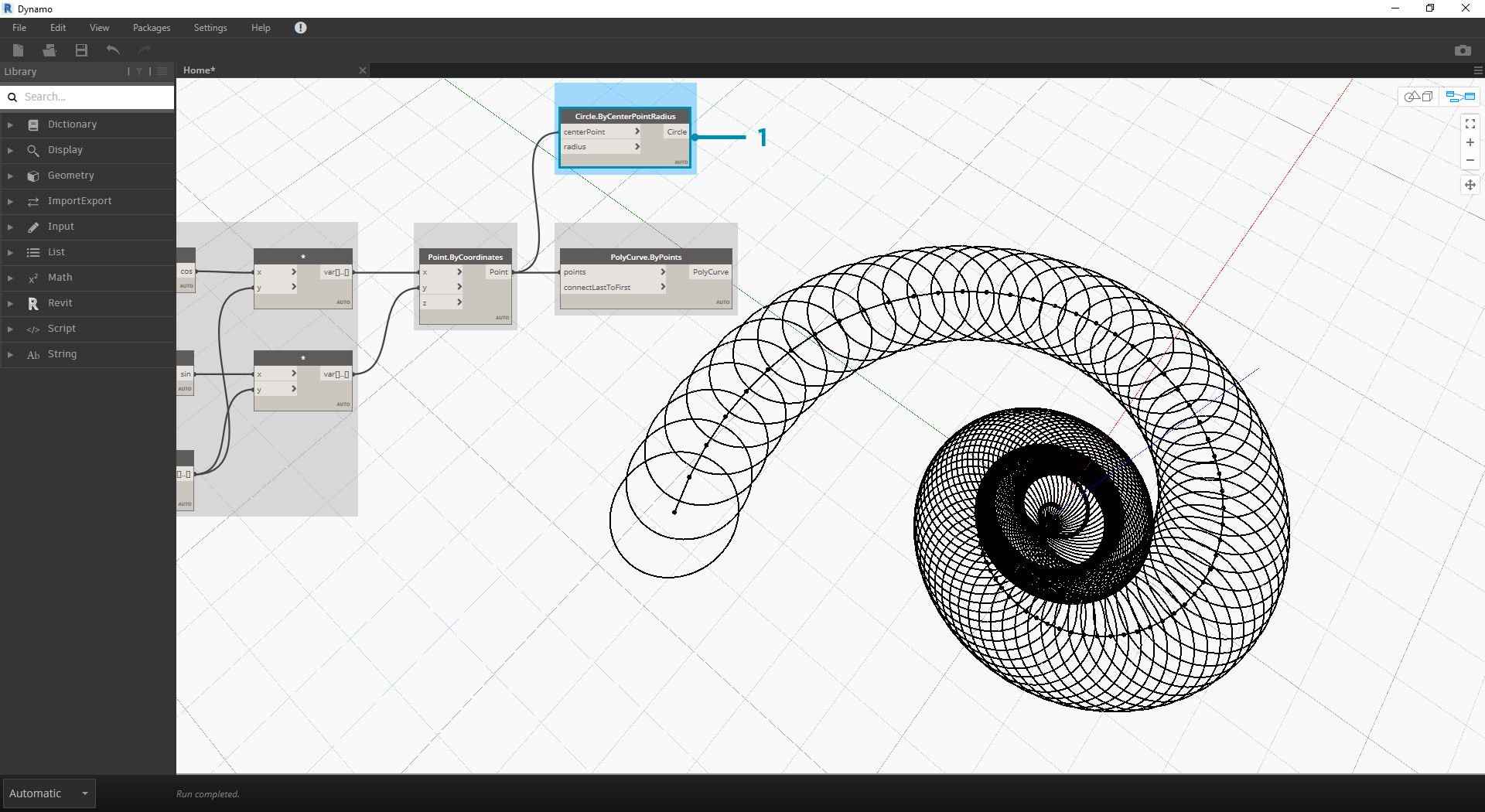
1. Polycurve.ByPoints：同样，这是上一练习中的节点，我们将用作参照。
2. Circle.ByCenterPointRadius：我们将在此处使用 Circle 节点，其输入与上一步相同。半径值默认为 1.0，因此可以看到圆即时输出。这些点与原点之间的分离程度立即清晰可辩。

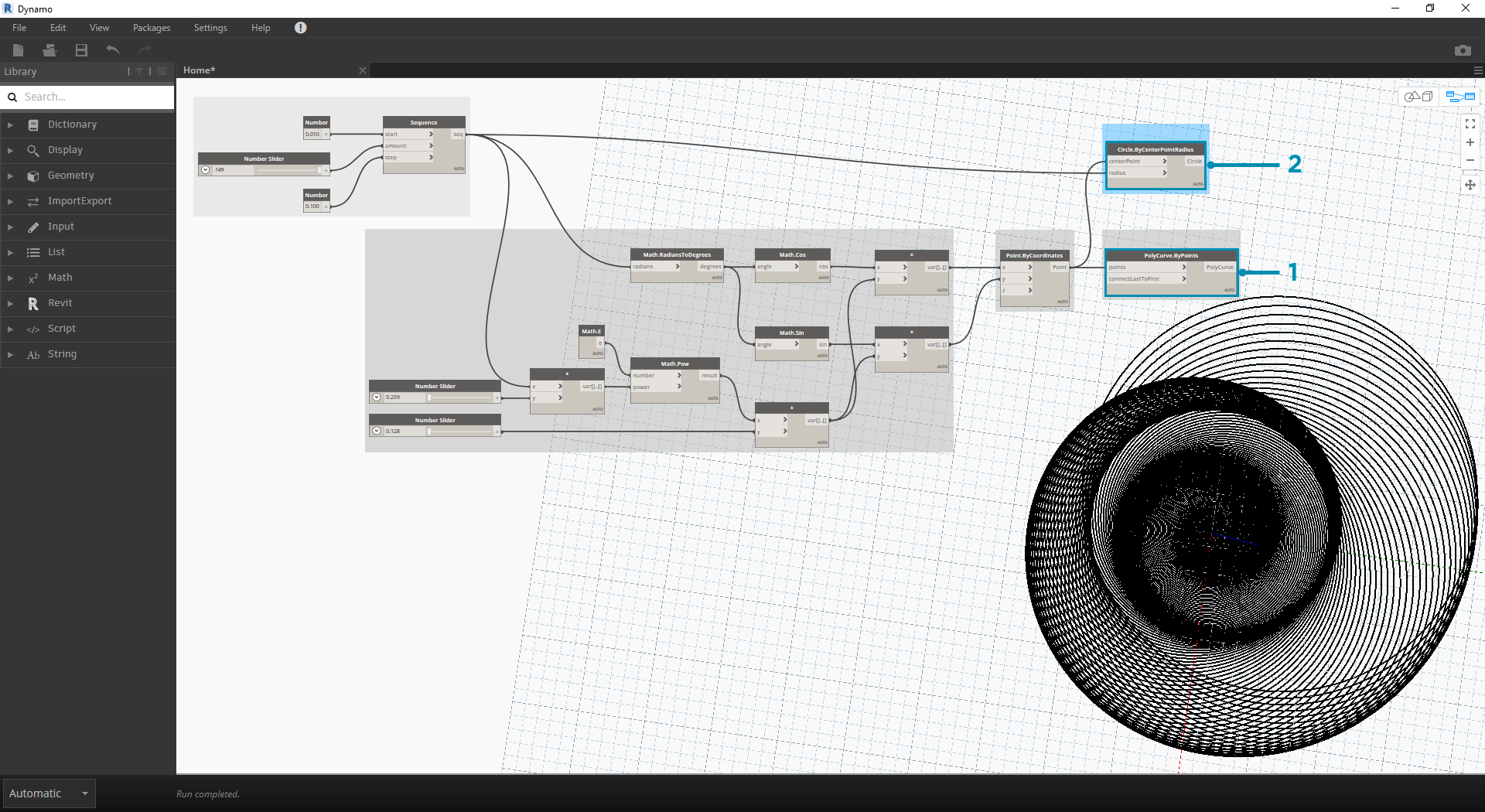
1. Circle.ByCenterPointRadius：要创建更动态的圆阵列，我们会将原始数字序列（即“t”序列）插入半径值。
2. Number Sequence：这是“t”的原始数组。通过将其连接到半径值，圆心仍与原点进一步偏离，但圆的半径不断增大，从而创建一个时髦的 Fibonacci 圆图。如果使其成为三维形式，即可获得奖励积分！

从 Nautilus 到 Phyllotaxis 图案

现在，我们已创建一个圆形 Nautilus 壳，接下来我们转到参数化栅格。我们将在 Fibonacci 螺旋上使用基本旋转来创建 Fibonacci 栅格，然后在向日葵种子生长后对结果进行建模。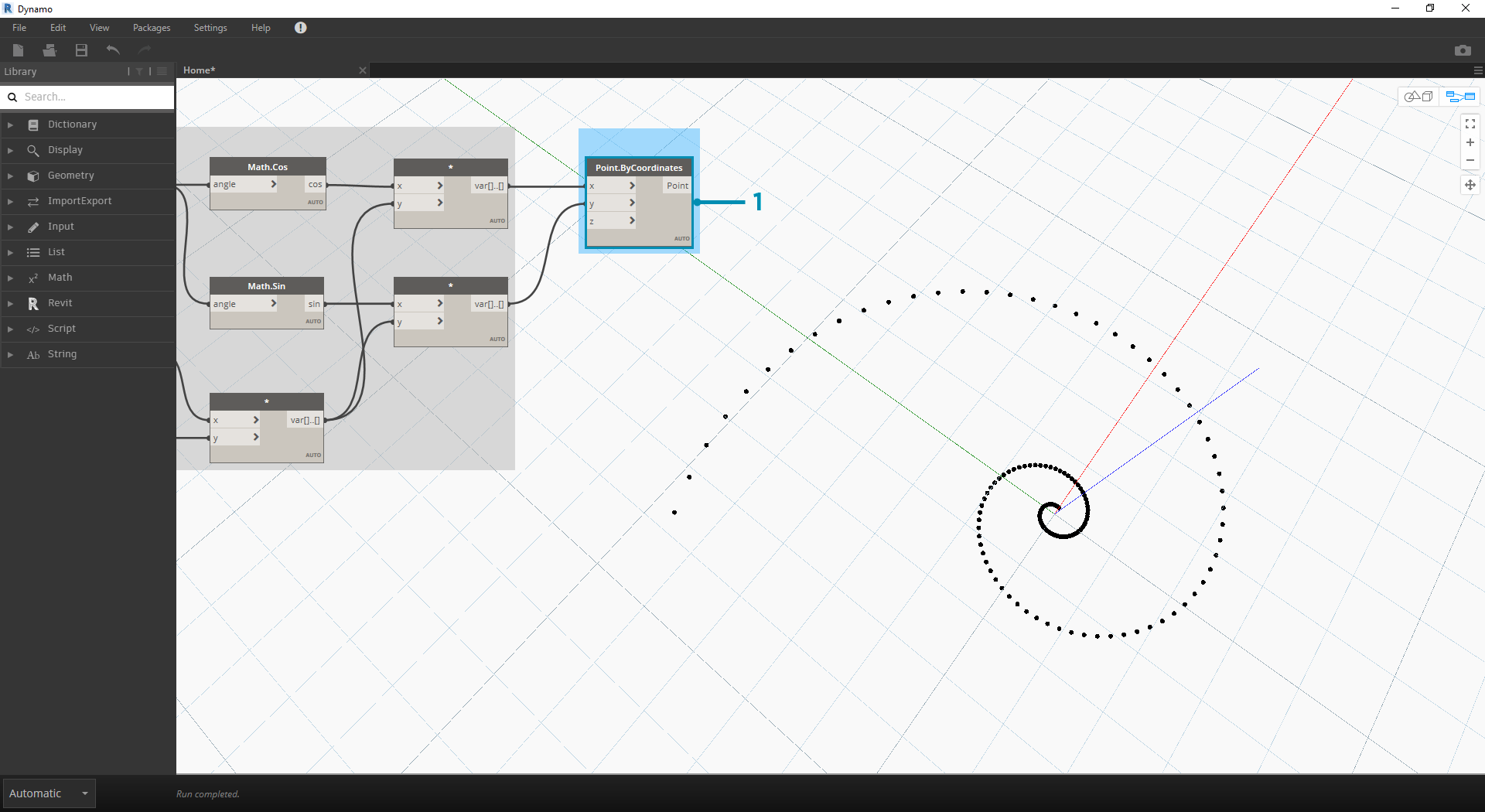

1. 同样，作为跳跃点，我们从上一练习的相同步骤开始：使用 Point.ByCoordinates 节点创建点的螺旋阵列。

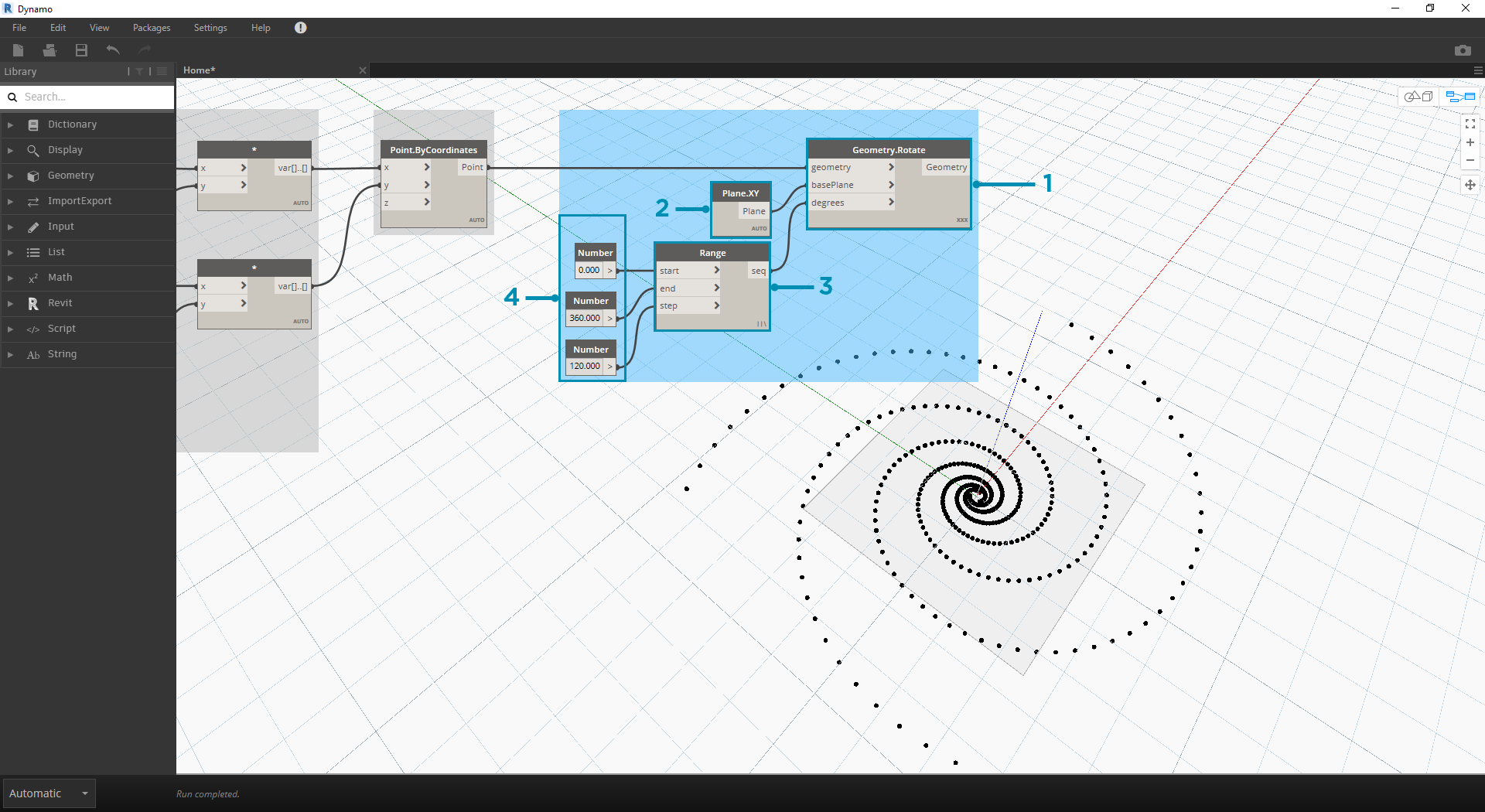
1. Geometry.Rotate：有多个 Geometry.Rotate 选项；请务必选择将 geometry、basePlane 和 degrees 作为其输入的节点。将 Point.ByCoordinates 连接到几何图形输入。
2. Plane.XY：连接到 basePlane 输入。我们将绕原点旋转，该原点与螺旋的底部位置相同。
3. Number Range：对于度数输入，我们要创建多个旋转。我们可以使用“数字范围”组件快速完成此操作。将其连接到 degrees 输入。
4. Number:：要定义数字范围，请按垂直顺序将三个数字节点添加到画布。从上到下，分别指定值 0.0,360.0, 和 120.0。这些驱动螺旋的旋转。将三个数字节点连接到相应节点后，请注意 Number Range 节点的输出结果。

我们的输出开始类似于旋涡。我们调整一些 Number Range 参数，看一看结果如何变化：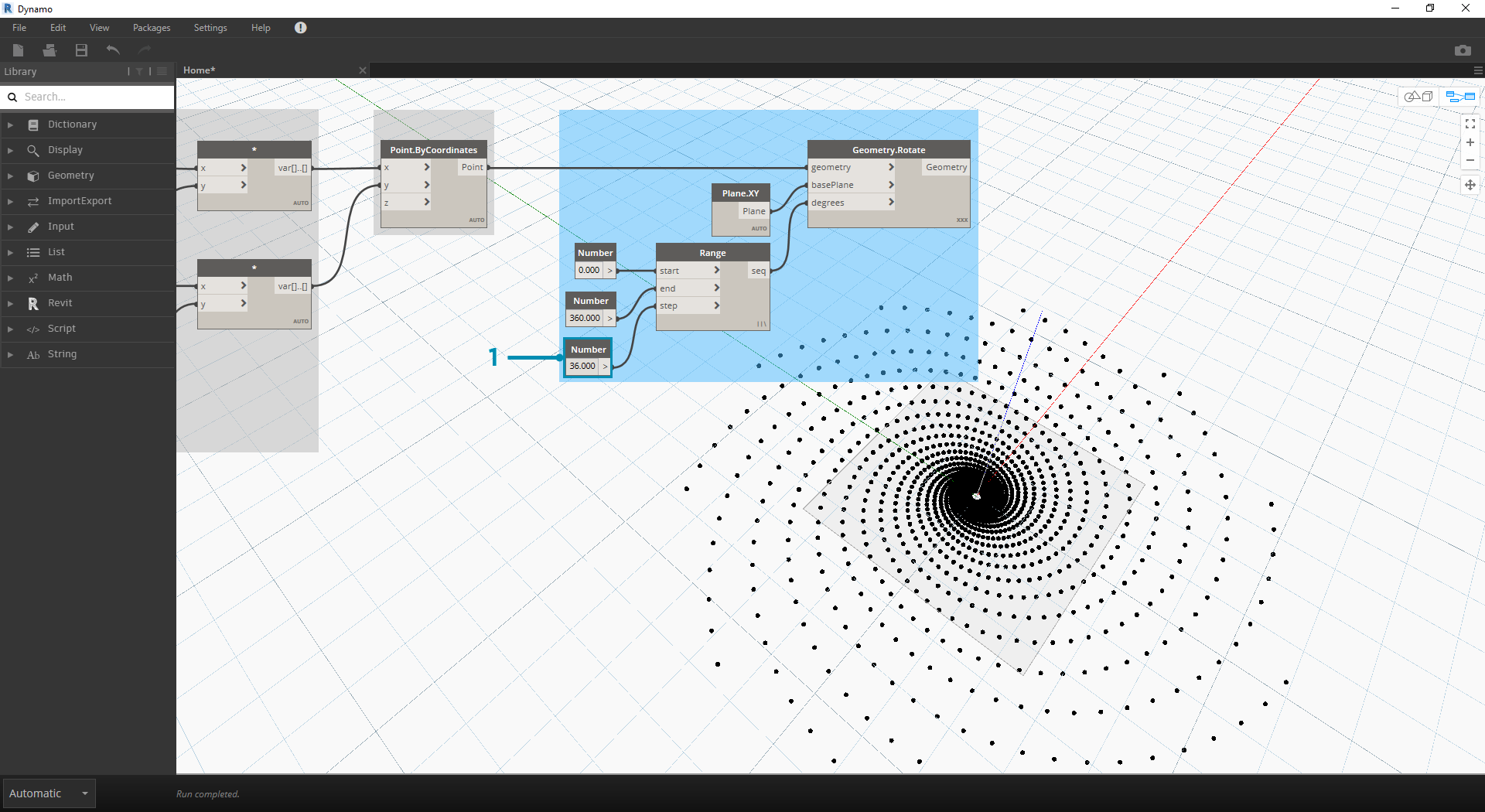

1. 将 Number Range 节点的步长从 120.0 更改为 36.0。请注意，这将创建更多旋转，因此会为我们提供更密集的栅格。

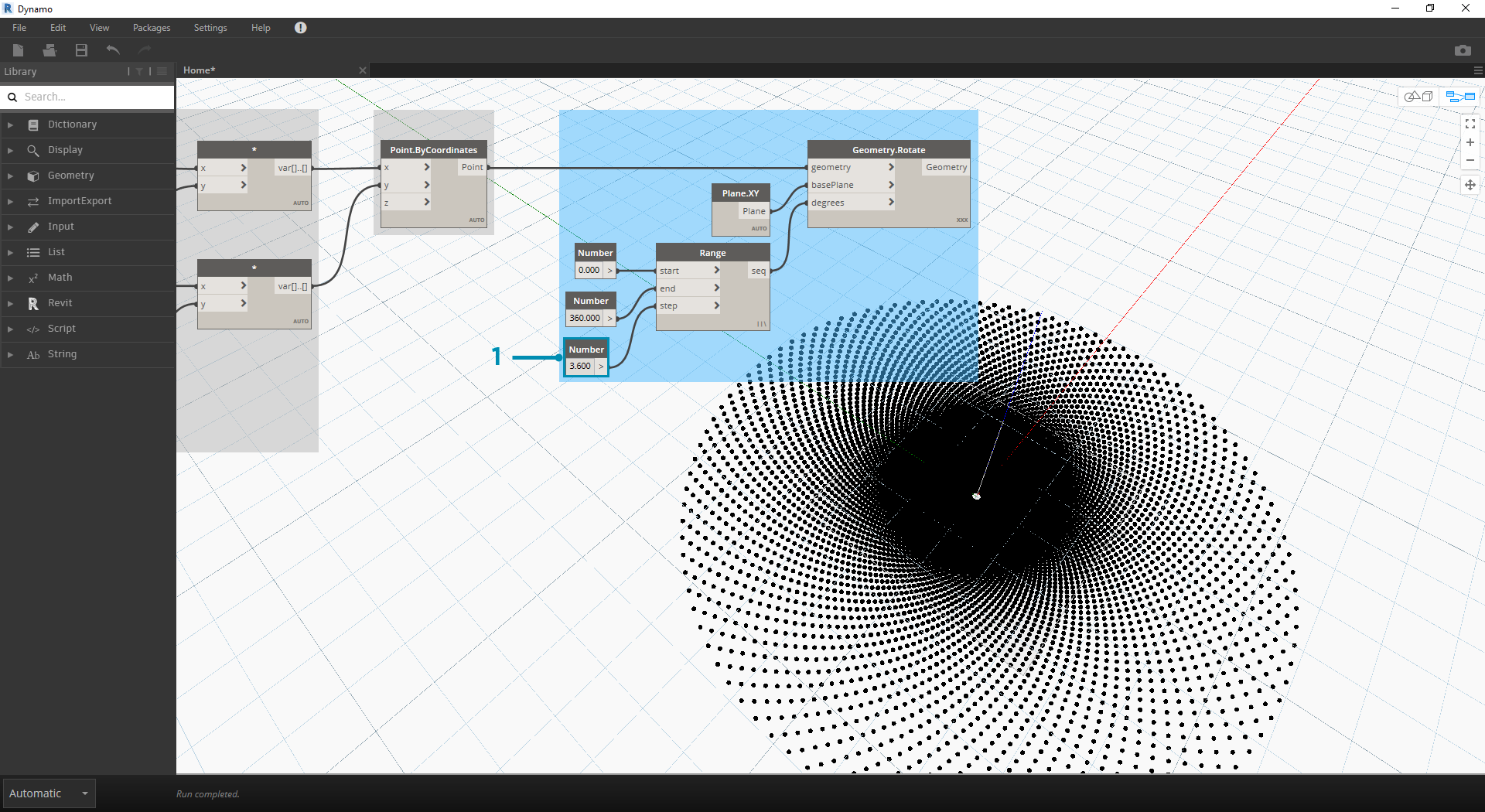
将 Number Range 节点的步长从 36.0 更改为 3.6。现在，我们得到更密集的栅格，但螺旋的方向性尚不楚。 --我们创建了一个向日葵。--