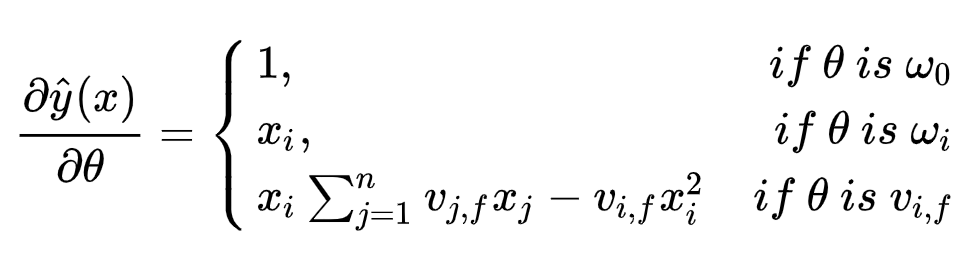FM（Factorization Machines）即因子分解机，在计算广告和推荐系统中，CTR（click-through rate）是非常重要的一个环节，判断一个物品是否进行推荐需要根据CTR预估的点击率排序决定。在进行CTR预估时，除了单特征外，往往要对特征进行组合，常用方法有：

• 人工特征 + LR
• GBDT + LR

• FM

  1. 特征组合

  FM是在LR的基础上，增加特征组合项得到的多项式模型。二阶多项式模型表达式如下：
  
  其中代表样本的特征数量，是第个特征的值，是模型参数。可看出组合特征的参数共有个，任意两个参数都是独立的。
  但面对稀疏性强的数据，二次项参数的训练是很困难的：二次项参数的训练需要大量同时非零的样本，否则梯度为0无法进行更新。但由于样本本就是稀疏数据，则满足同时非零的数据非常少，训练样本不足，参数不准确，严重影响模型的性能。

  2. 矩阵分解

  所有二次项参数可以组成一个对称矩阵（任意实对称矩阵都有N个线性无关的特征向量），则对该对称矩阵进行分解：
  
  即：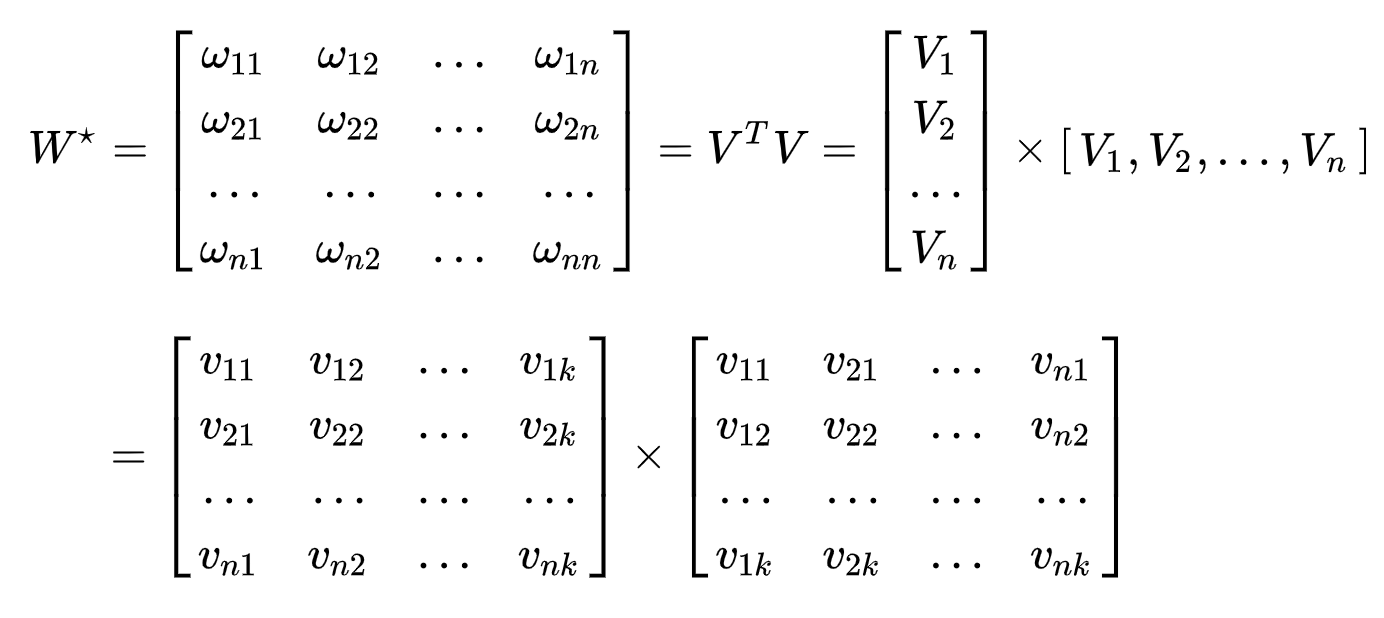
  
  其中就是第个特征的隐向量，，特征分量的交叉项系数等于两隐向量的内积，即，这就是FM模型的核心思想。此时FM模型为：
  
  此时FM模型的复杂度为，可通过变换，将FM的二次项进行花剑，复杂度优化为，优化方法如下：
  

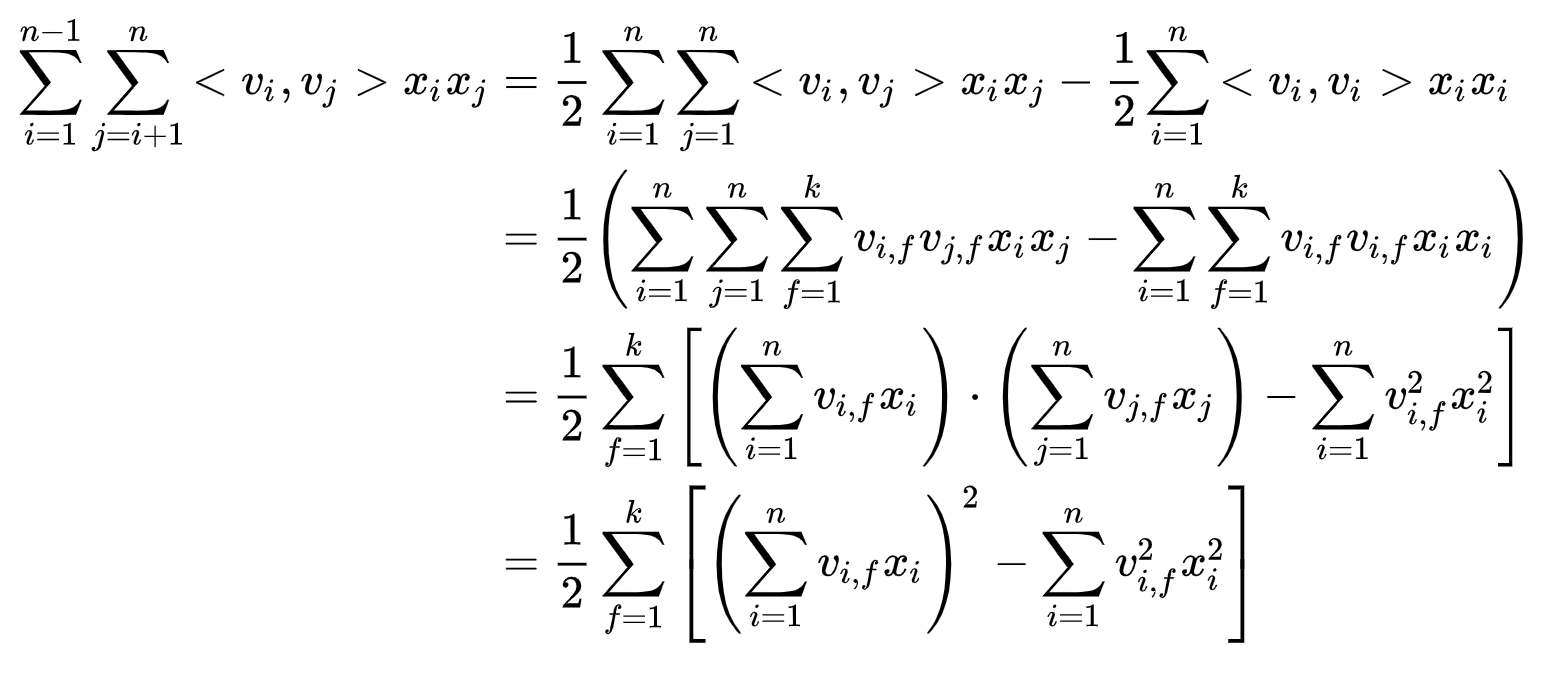
  3. TensorFlow实现FMLayer

  class FM_Layer(Layer):
    def __init__(self, feature_columns, k, w_reg, v_reg):
        super().__init__()
        self.feature_columns = feature_columns
        self.index_map = []
        self.feature_num = 0
        for fea in self.feature_columns:
            self.index_map.append(self.feature_num)
            self.feature_num += fea['feat_num']
        self.k = k
        self.w_reg = w_reg
        self.v_reg = v_reg
    def build(self, input_shape):
        self.w0 = self.add_weight(name='w0',
                                  shape=(1,),
                                  trainable=True)
        self.w = self.add_weight(name='w',
                                 shape=(self.feature_num, 1),
                                 regularizer=l2(self.w_reg),
                                 trainable=True)
        self.v = self.add_weight(name='v',
                                 shape=(self.feature_num, self.k),
                                 regularizer=l2(self.v_reg),
                                 trainable=True)
    def call(self, inputs, **kwargs):
        '''
            数据预处理方式：
            sparse feature: label encode
            dense feature: 离散分箱
        '''
        inputs = inputs + tf.convert_to_tensor(self.index_map)
        # first order
        first_order = self.w0 + tf.reduce_sum(tf.nn.embedding_lookup(self.w, inputs), axis=1)  # (batch, 1)
        # second order
        embedding_inputs = tf.nn.embedding_lookup(self.v, inputs)  # (batch, input_length, embed_dim)
        square_sum = tf.square(tf.reduce_sum(embedding_inputs, axis=1))  # (batch, embed_dim)
        sum_square = tf.reduce_sum(tf.square(embedding_inputs), axis=1)  # (batch, embed_dim)
        second_order = 0.5 * tf.reduce_sum(square_sum - sum_square, axis=1, keepdims=True)  # (batch, 1)
        return first_order + second_order

  4. 梯度求解

  采用随机梯度下降法SGD求解参数如下：