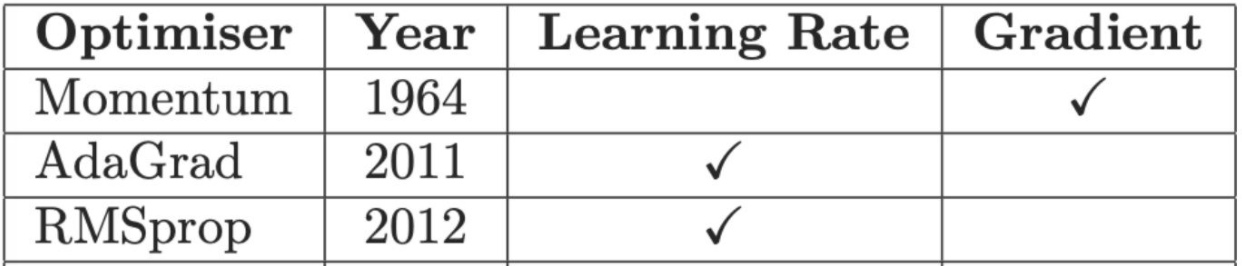
一阶优化算法基本情况如下，其中又可分类为：

• 基本算法：SGD、Momentum
• 自适应学习率算法：AdaGrad、RMSProp、Adam

算法名称、提出时间、是否修改lr、gradient

1. 基本算法

1. 随机梯度下降法

优点：

  - 相比原始梯度下降法每次更新参数都要用到所有数据，SGD每次只选择样本的一个子集经计算进行参数更新，速度更快。

缺点：

  - 每次迭代并不一定都是模型整体最优化的方向，若样本噪声较多，则会影响收敛速度。

2. 使用动量的随机梯度下降法

2. 自适应学习率算法

1. AdaGrad算法

梯度下降对环境的感知是指在参数空间中，根据不同参数的一些经验型判断，自适应地确定参数的学习速率，不同参数的更新步幅是不同的；
AdaGrad希望更新频率低的参数可以拥有较大的更新步幅，而更新频率高的参数的步幅可以减小。采用“历史梯度平方和”来衡量不同参数的梯度的更新频率。

2. RMSProp算法

3. Adam算法

Adam一阶矩，即过往梯度与当前梯度的平均，体现了惯性保持；
Adam二阶矩，即过往梯度平方与当前梯度平方的平均，类似AdaGrad方法（但不同，不是从一开始的累加），体现了环境感知能力，为不同参数产生自适应的学习速率。
注意到，在迭代初始阶段，和 有一个向初值的偏移（过多的偏向了 0）。因此，可以对一阶和二阶动量做偏置校正 (随着迭代次数增加逐渐失效），即：