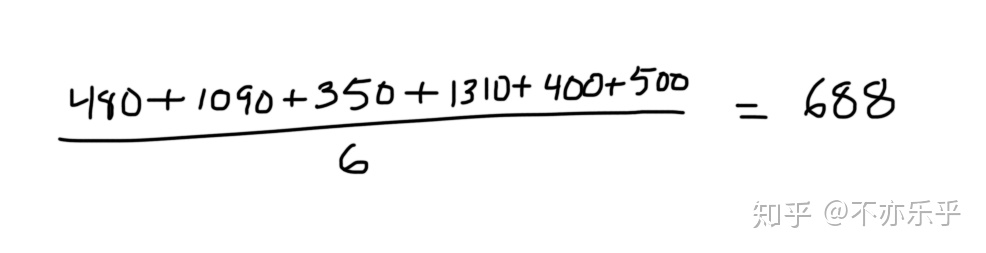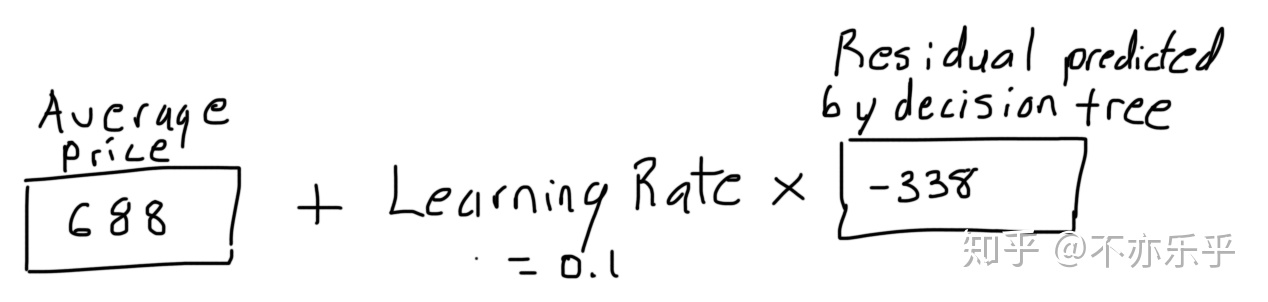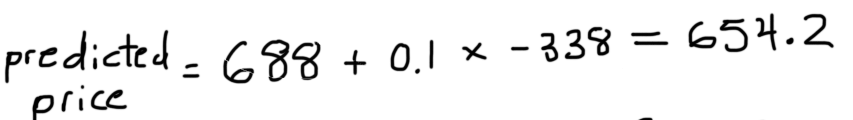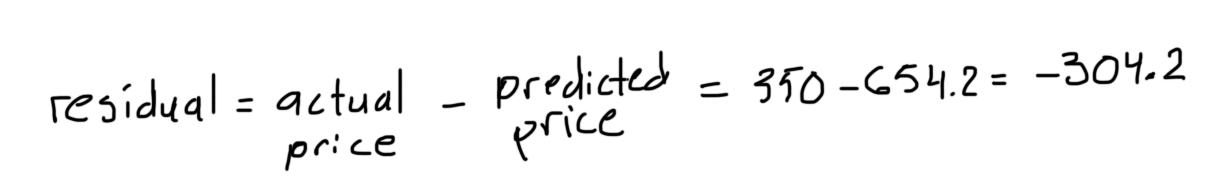GBDT

0. boosting和bagging简述

boosting是一种可将许多弱学习器组合成为一个强学习器的算法，其中每个弱学习器的bias较大，最终的强学习器bias较低，boosting主要关注降低bias。
bagging是许多较强的学习器进行投票，得到最终结果。其中每个学习器的bias相对较小，得到的投票结果bias依然较小。但因为每个学习器较强，容易发生过拟合，产生较大方差，所以从偏差-方差分解的角度看，bagging主要关注降低方差。

1. GBDT概述

GBDT全名梯度提升决策树，使用的是boosting思想，可以看做是很多个基模型的线性相加，其中的基模型就是CART回归树。

2. 算法流程

维基百科对gbdt算法流程的介绍如下：

只简单提几点：

• 这里的讨论都是基于误差函数为均方误差 ，此时误差函数负梯度方向(残差)即：

• 初始学习器 等于对所有训练集求取的均值，再根据上面的公式计算当前残差，此时训练样本从 变为
• “2”中第m次循环，到“2.2”处，用当前“训练集” 构建一个CART回归树
• 为了防止训练样本中噪声对模型泛化能力的影响(避免过拟合)，“2.3”处引入合适的学习率，并在“2.4”中将新的树并入模型
• 若循环未结束，在第m+1轮循环的“2.1”处，根据 产生新的“训练集”

• 循环结束，此时

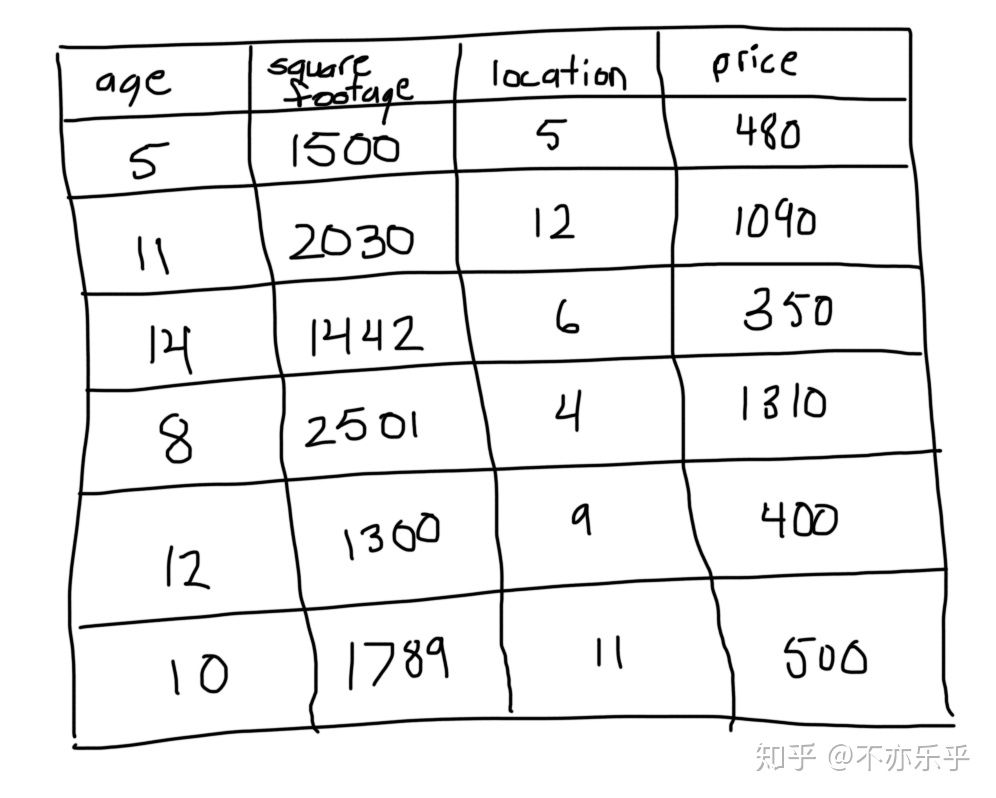
  3. GBDT实例

  用GBDT预测房价，训练集如下：
  

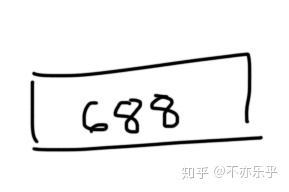
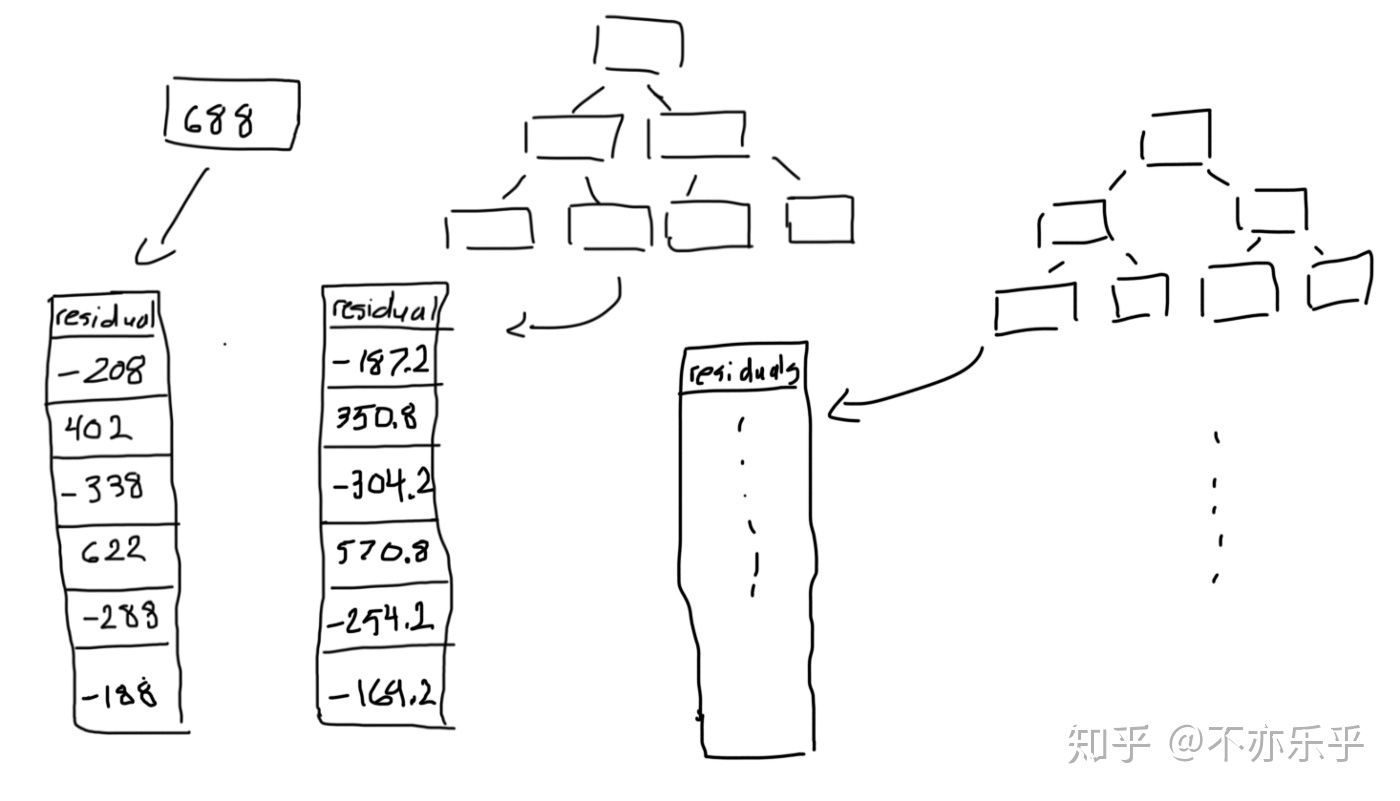
  step 1：首先对训练集所有价格求均值：

  
  所以第一个学习器(预测值) 为：
  

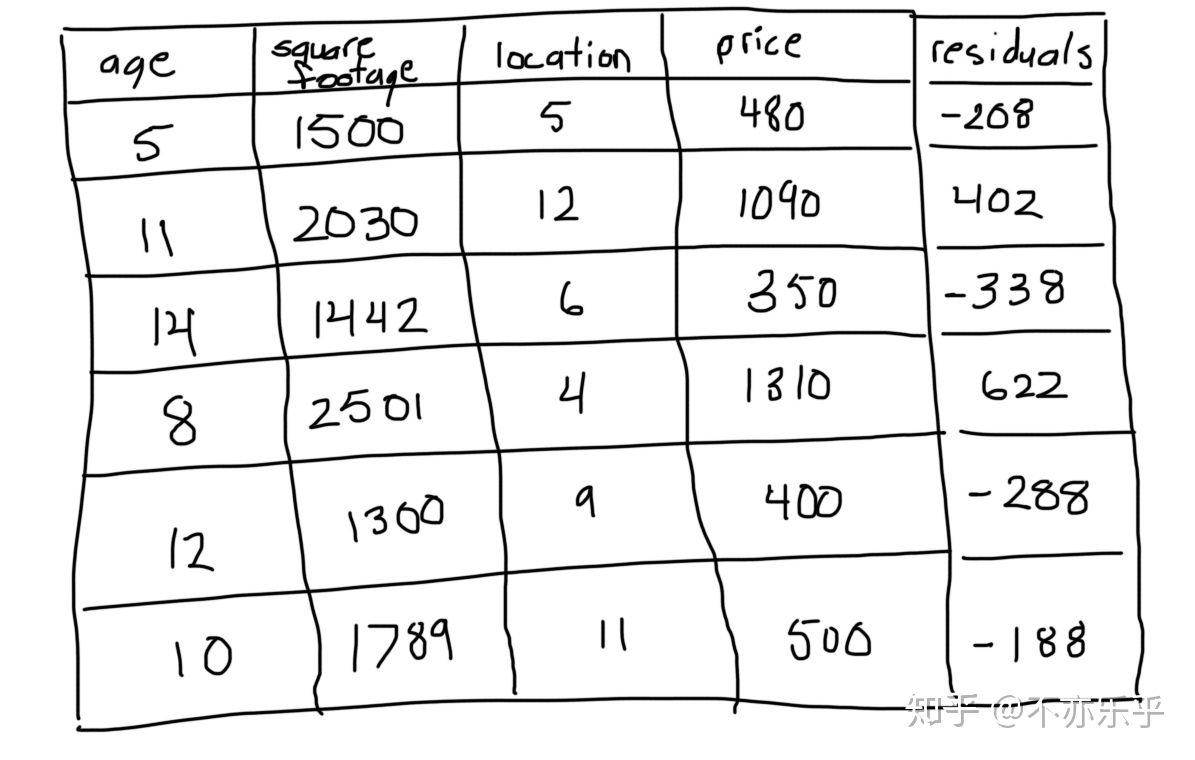
  step 2：根据当前预测值，计算每个样本残差：

  
  此时当前训练集变为：
  

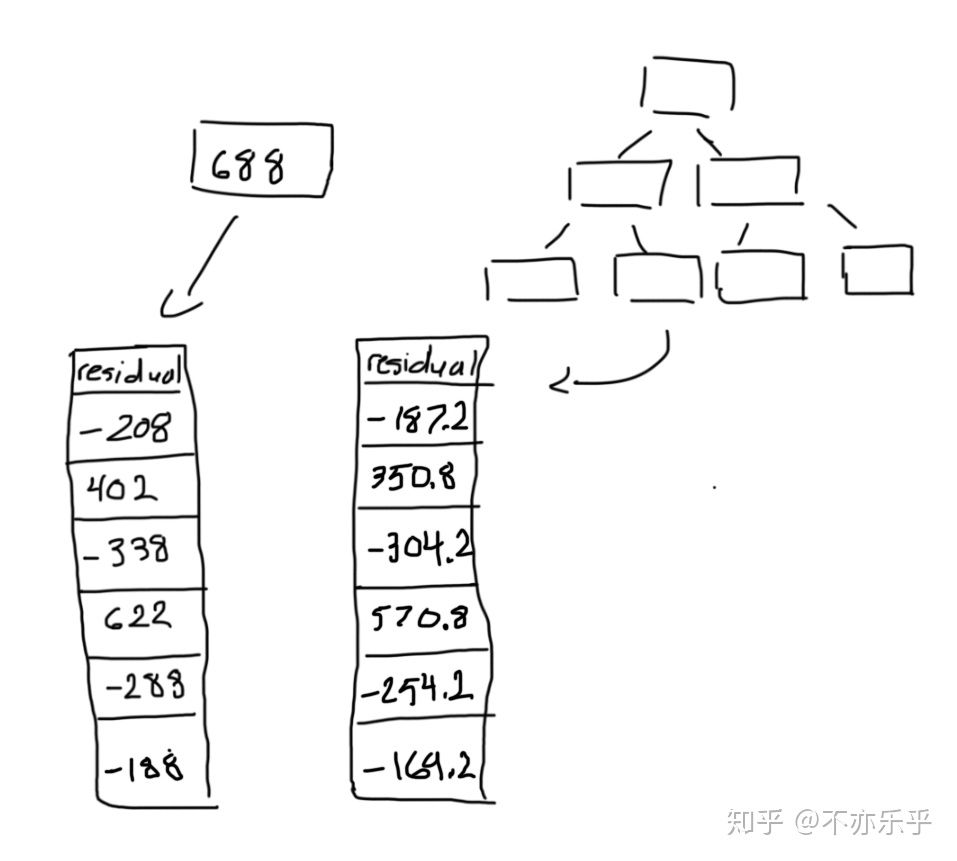
  step 3：根据新的“训练集”，以残差代替房价为target构建高度为3的CART回归树：

  
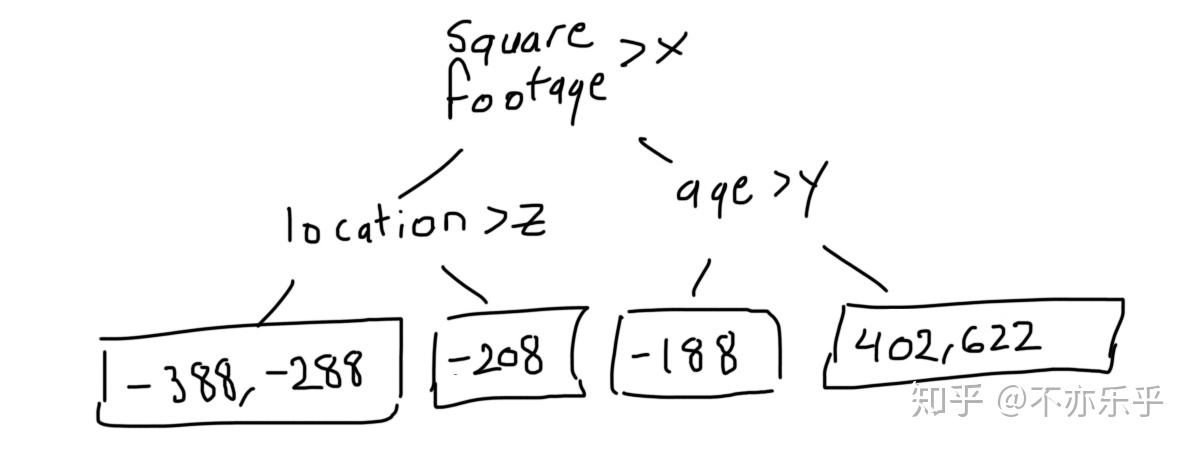
  第1、4个节点对应多个样本，取他们对应的残差值的中间值为该叶结点预测值：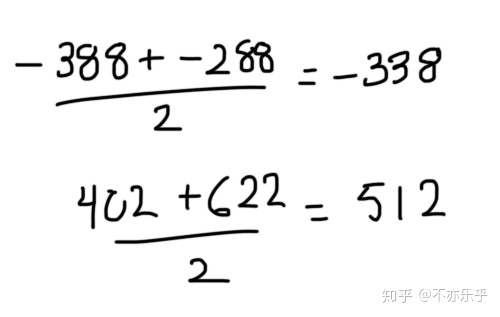
  
  所以这个CART回归树变为：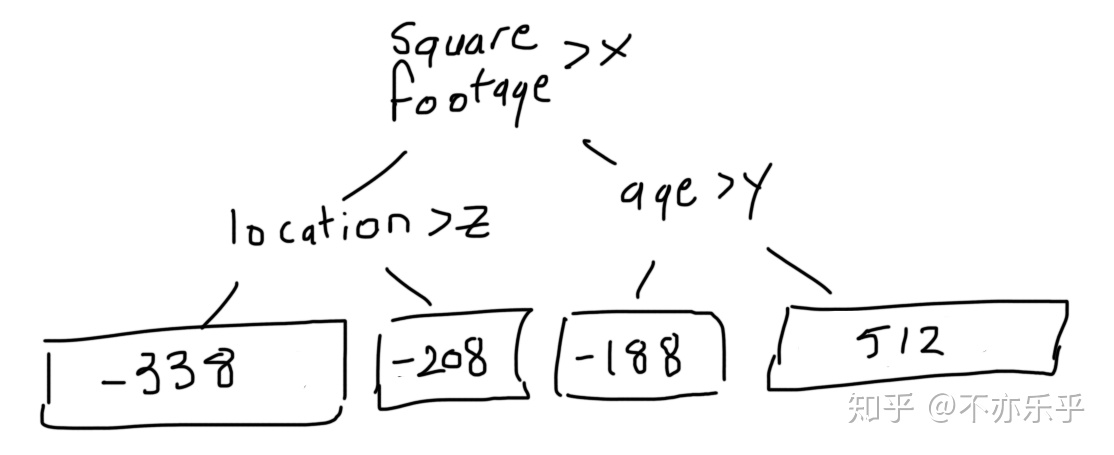
  

  step 4：得到新的学习器(预测值) ：

  

  step 5：计算新残差：

  

  step 6：重复step 3～5，直到完成规定的迭代次数：

  

  step 7：完成训练后，即可用测试样本点在所有回归树中的预测值的叠加值完成预测

  

  4. GBDT的优点和局限性

  4.1 优点

• 预测阶段的计算速度快，树与树之间可并行化计算

• 在分布稠密的数据集上，泛化能力和表达能力都很好

• 采用决策树作为弱分类器使得GBDT模型具有较好的解释性和鲁棒性，能够自动发现特征间的高阶关系

  4.2 局限

• GBDT在高维稀疏的数据集上，表现不如支持向量机或者神经网络

• GBDT在处理文本分类特征问题上，相对其他模型的优势不如它在处理数值特征时明显
• 训练过程需要串行训练，只能在决策树内部采用一些局部并行的手段提高训练速度