1. Abstract

在实践中发现多任务学习模型中存在seesaw phenomenon现象，即一个任务的效果提高总是以其他任务效果变差为代价，为此本文提出PLE模型，主要方法有：

1. a PLE model：在MMOE基础上提出task specific expert，缓解跷跷板现象
2. a progressive routing mechanism：使用动态任务权重调节机制

网络结构如下：

2. Seesaw Phenomenon in MTL For Recommendation

实验发现，受限于MTL的shared bottom结构，过去的多任务学习模型很难做到多个任务共同从多任务学习模型中受益，一个任务效果提高常伴随其他任务效果得不到提高甚至变差的代价，称这种现象为跷跷板现象。以两个任务为例，与单任务模型效果比较结果如下：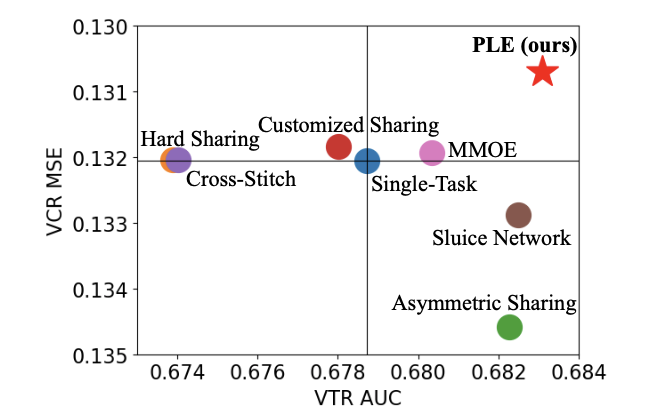

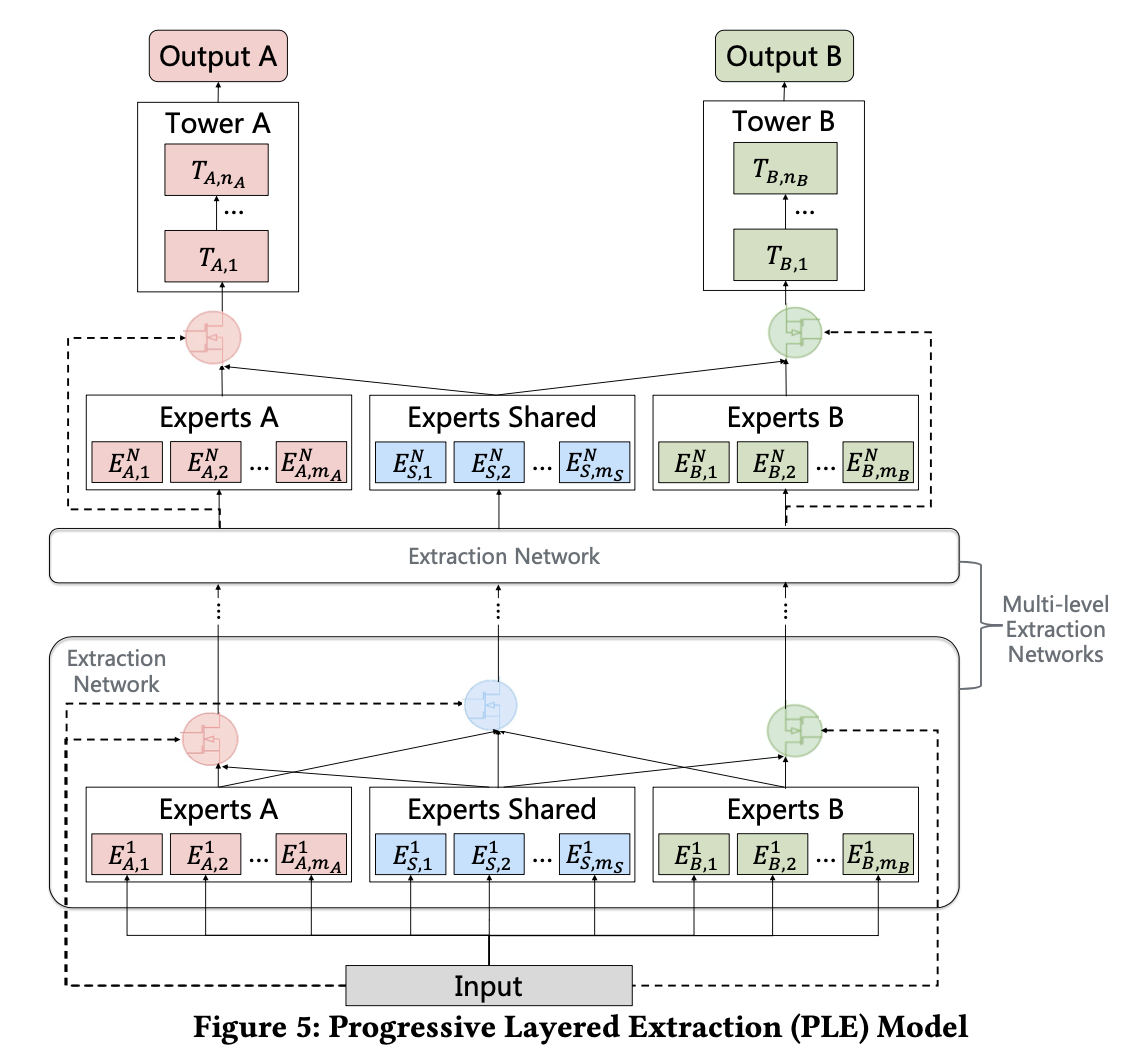
3. Progressive Layerd Extraction

为解决seesaw phenomenon和negative transfer现象，在网络中设计PLE层，在PLE层中：

  - 每个task's tower network只接收shared expert network和其自身的task-specific network信息；
  - 各task's tower network不再与其他任务的task-specific expert network连接，实现多任务学习模型各任务间既能学习到共同点，又不会损害其他任务效果。

PLE的门网络计算方式如下：
对于任务，首先将task-specific network和shared expert network的结果concat到一起，得，

计算上述expert network与任务的相关性，即gate network，

结合，获得task’s tower network输入，

计算任务结果，

其中为task’s tower network函数。

CGC（Customized Gate Control）Model网络结构如下：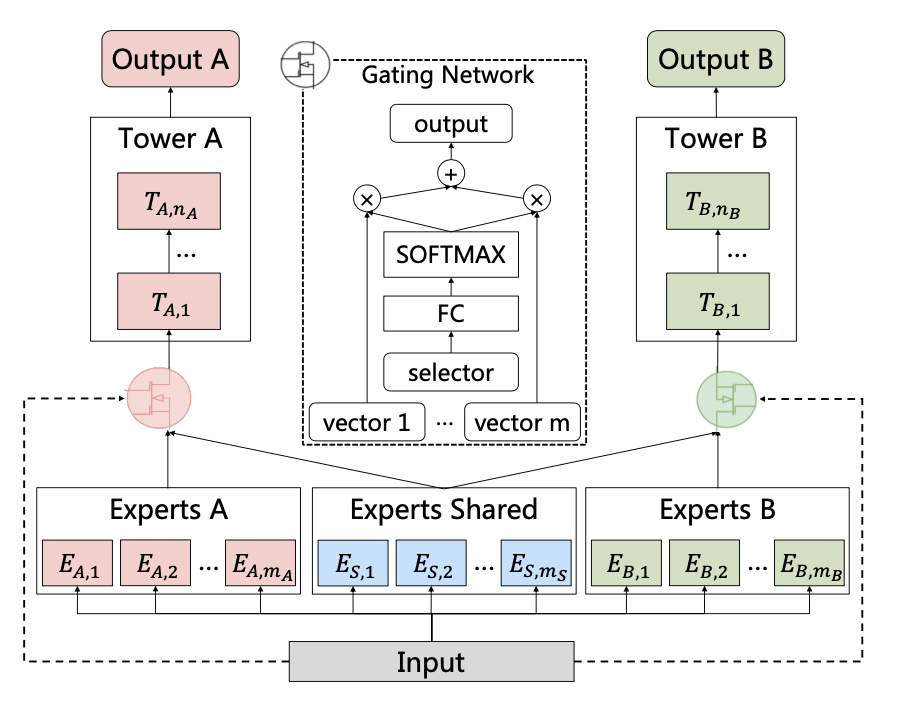

4. Experiment

为解决多任务学习模型中的样本选择偏差，设计特殊损失函数，仅对多个任务协变量交集进行误差计算：

其中，当输入属于任务时取1，否则取0。
设计动态任务权重调节机制；

总体损失函数为：

实验效果对比如下：