激活函数相当于对坐标轴空间进行扭曲 是深层神经网络具有强大拟合能力的主要原因

更新：
线性模型是机器学习领域中最基本的模型，它可以高效地拟合数据。然而真实情况中，我们往往会遇到线性不可分问题，需要非线性变换对数据的分布进行重新映射。在神经网络中通过在线性变换后叠加一个激活函数实现这一目标，同时也避免多层网络等效于单层线性函数，从而获得更强大的学习与拟合能力。
1. 激活函数及其导数
Sigmoid：


Tanh：


ReLU：


其中Sigmoid和Tanh会导致梯度消失现象。
Softmax:

2. ReLU相对Sigmoid、Tanh优点是什么？局限性？改进？
优点：

  1. 计算角度，Sigmoid、Tanh均需要计算指数，复杂度高，而ReLU只需要一个阈值即可得到激活值
  1. ReLU的非饱和性可以有效解决梯度消失问题，提供相对宽的激活边界
  1. ReLU的单侧抑制提供了网络的系数表达能力

局限：

  1. 训练过程中会导致神经元死亡的问题。小于0的数据经过ReLU被置0，且在之后也不会被任何数据激活，不对任何数据产生响应。在实际训练过程中若学习率设置较大，会导致超过一定比例的神经元不可逆死亡，进而参数梯度无法更新，整个训练过程失败。

改进：

  1. LeakyReLU（a为一个较小常数）

  1. PReLU（a为一个可学习参数）

神经网络的激励函数（activation function）是一群空间魔法师，扭曲翻转特征空间，在其中寻找线性的边界。

1. 当神经网络中没有激活函数

利用我们单层的感知机, 用它可以划出一条线, 把平面分割开：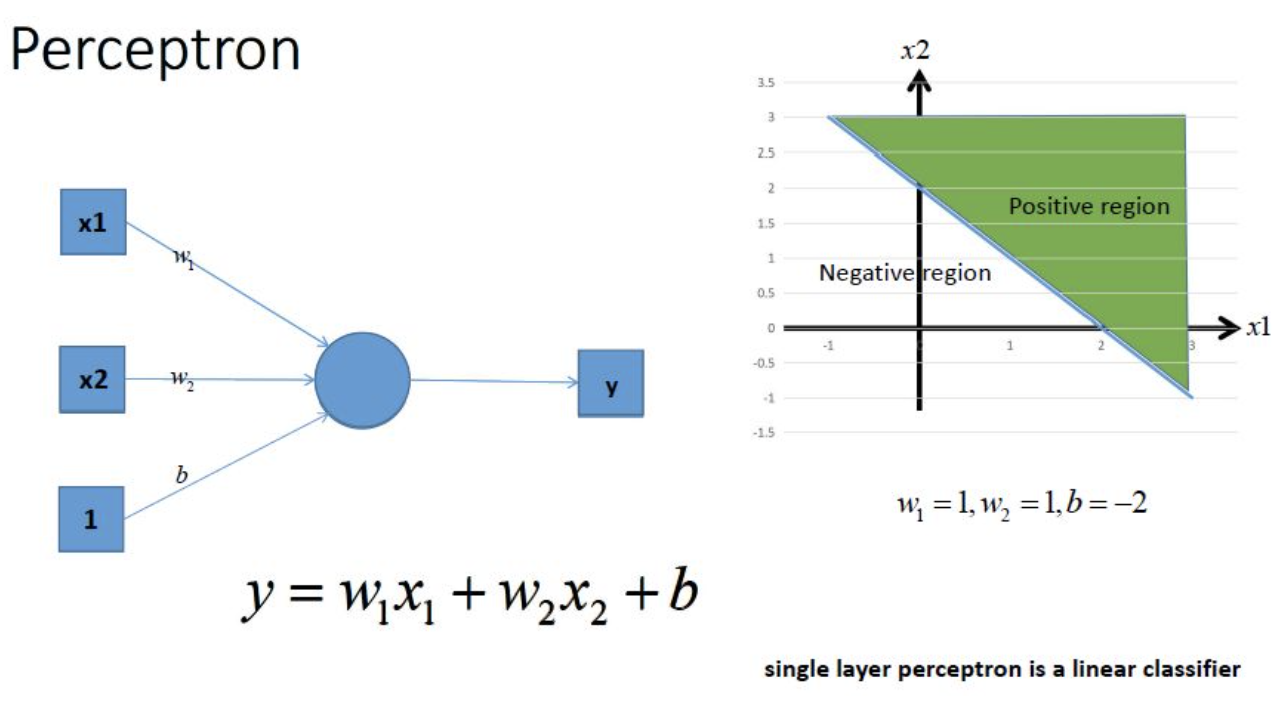

很容易能够看出，我给出的样本点根本不是线性可分的，一个感知器无论得到的直线怎么动，都不可能完全正确的将三角形与圆形区分出来，那么我们很容易想到用多个感知器来进行组合，以便获得更大的分类问题，好的，下面我们上图，看是否可行：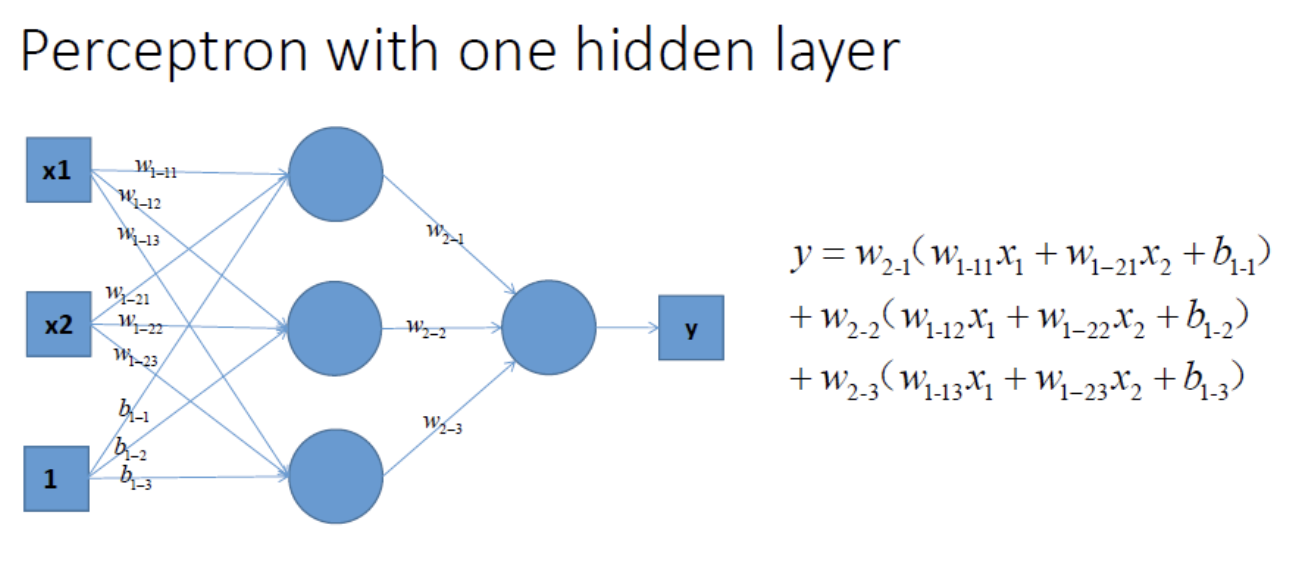

对图中式子，经过变换，可得：

由上式可知，当没有激活函数时，即使增加网络深度，仍然是一个线性函数，实质与单层网络没有差异，故仍不能解决非线性问题。

2. 使用激活函数

没有激活函数的神经网络，甚至连下面这样的简单分类问题都解决不了：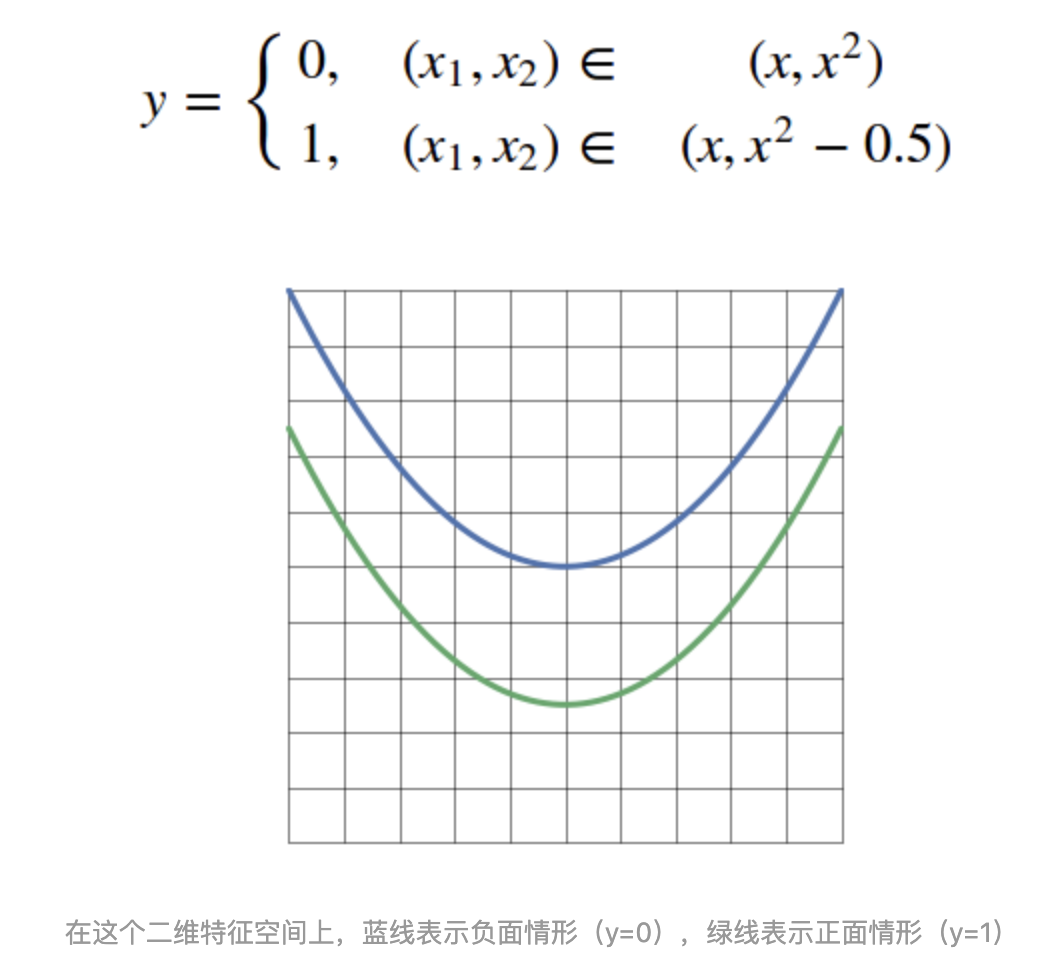

没有激励函数的加持，神经网络最多能做到这个程度：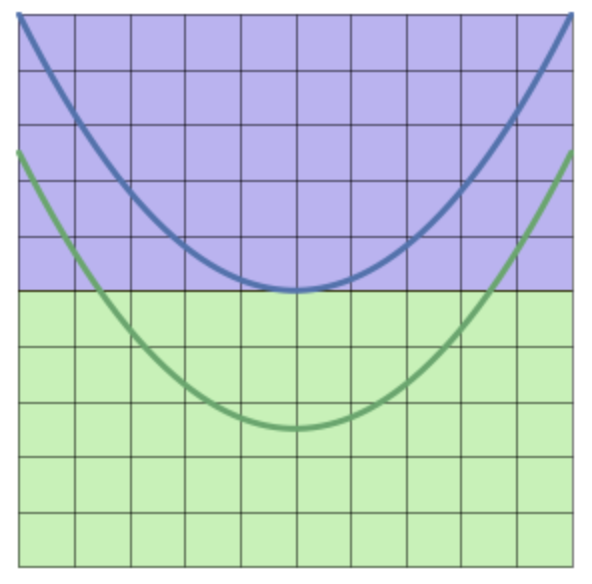

这时候，激励函数出手了，扭曲翻转一下空间：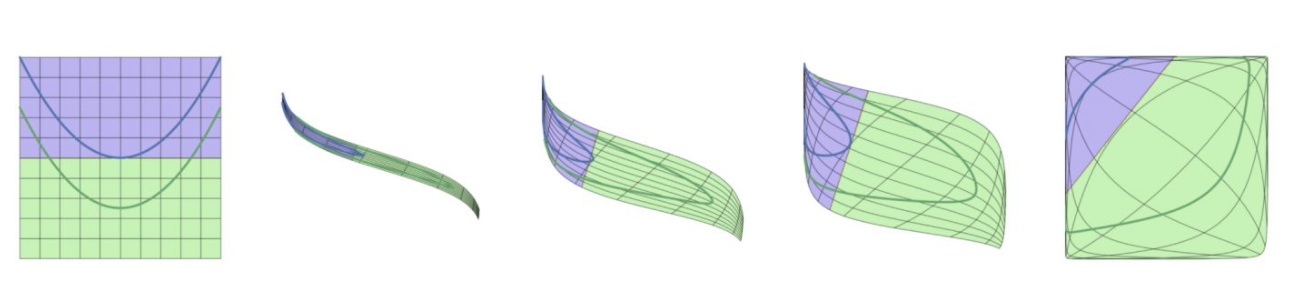

线性边界出现了！再还原回去，不就得到了原特征空间中的边界？
当然，不同的激励函数，因为所属流派不同，所以施展的魔法也各不相同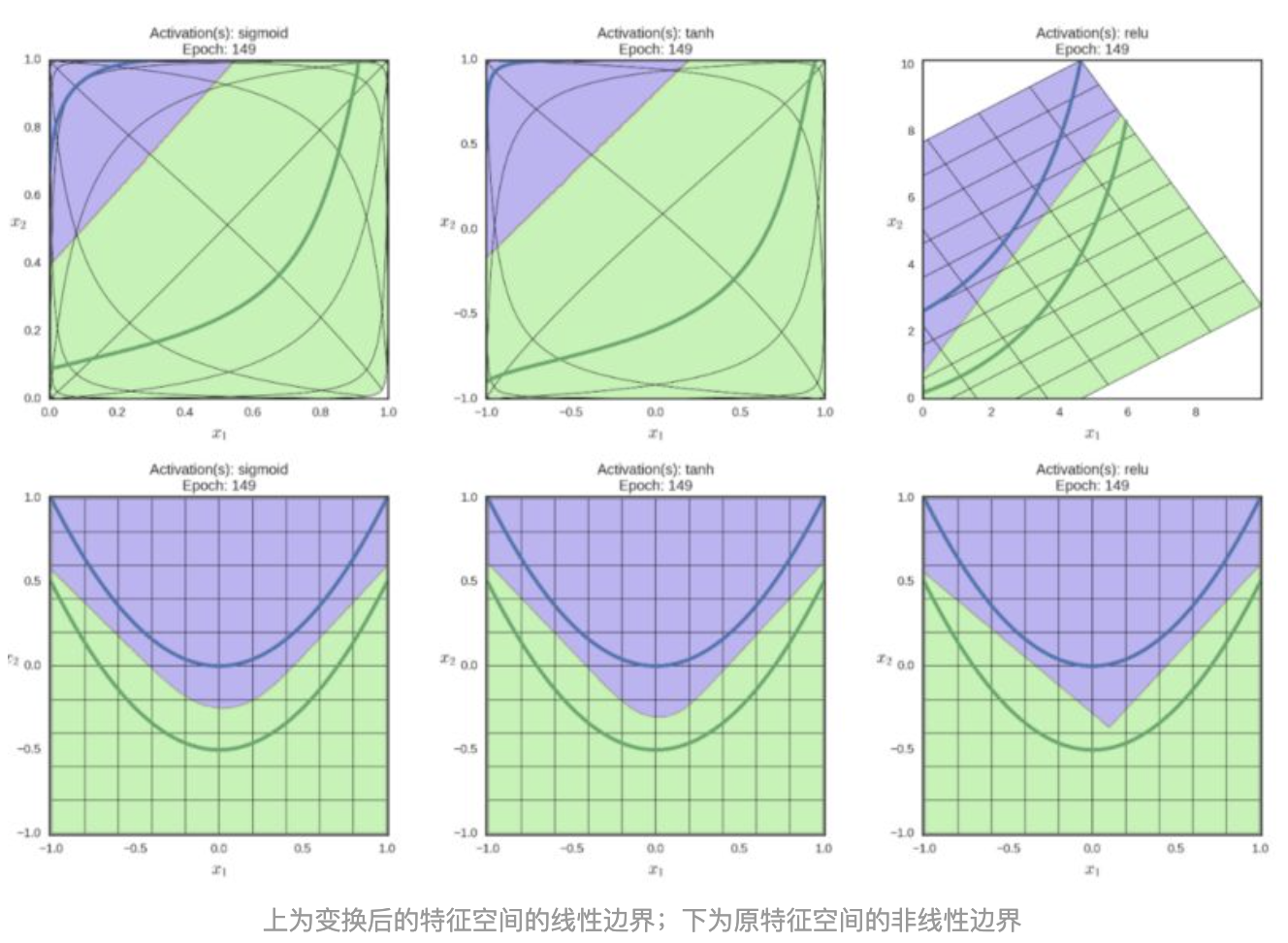

上图中，出场的三位空间魔法师，分别为Sigmoid、Tanh、ReLU。