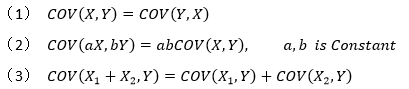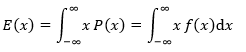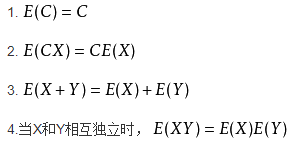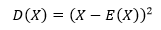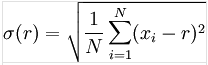1. 古典概率

1. 条件

1. (有限性) 试验结果只有有限个 (记为 n)

2. (等可能性) 每个基本事件发生的可能性相同

   2. 计算

   
   计算古典概率, 主要用到排列组合的知识，总结如下：
   (1) n个不同物件取r个不同的排列总数为：
   
   (2) n个不同物件取r个不同组合总数为：
   
   (3) n个相异物件分成k堆，各堆物件数分别为：
   

   2. 几何概率

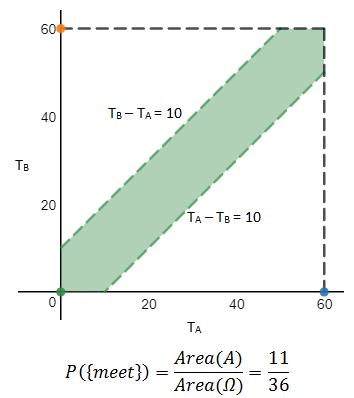
   甲、乙二人约定1点到2点之间在某处碰头，约定先到者等候10分钟即离去。设想甲、乙二人各自随意地在1～2点之间选一个时刻到达该处，问“甲、乙二人能碰上“这个事件meet的概率是多少？
   

   3. 全概率公式和贝叶斯公式

   1. 全概率公式

   

   2. 贝叶斯公式

   

   4. 期望

   1. 期望：反映随机变量平均取值的大小

   • 离散型期望：

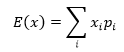
  - 连续型期望：

期望的性质：

2. 方差：衡量随机变量的离散程度

3. 均方差

4. 协方差：表示两个变量总体的误差

辨析：协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。协方差为0，表两个变量相互独立。

性质：