1. K-Means
1. 原理
K_Means算法的思想很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。令数据集中共n个样本,每个样本含m维特征,进行e次迭代,确定k个质心,则时间复杂度为:
假设簇划分为,则我们的目标是最小化平方误差
:
其中是簇
的质心:
如果我们想直接求上式的最小值并不容易,故K_Means采用启发式方法求解。求解过程如下图: 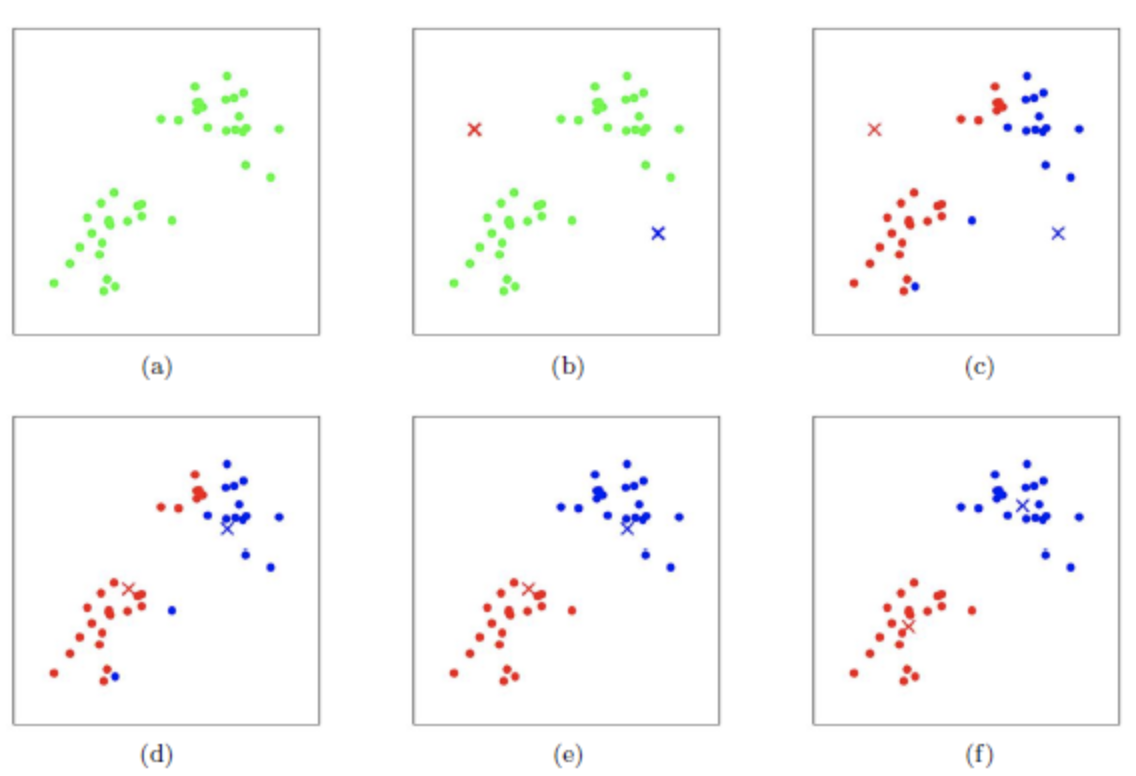
2. 初始化优化:K-Means++
K-Means初始化的质心的位置选择对最后聚类结果和运行时间都有很大影响,如果完全随机的选择,可能导致算法收敛很慢。K-Means++就是对K-Means随机初始化质心方法的优化:
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心- 对于数据集中的每一个点,计算它与已有中心中最近的距离- 选择一个新的数据点作为新的聚类中心,选择的原则是:较大的点,被选取作为聚类中心的概率较大- 重复上述步骤,直到选出k个聚类中心
3. 大样本优化:Mini Batch K-Means
如果样本量非常大,此时传统聚类非常耗时,在大数据时代,这样的场景越来越多,因此Mini Batch K-Means应运而生。
Mini Batch K-Means的思想是通过无放回的随机采样得到一个训练子集,计算k个聚类中心。
2. DBSCAN
1. 原理
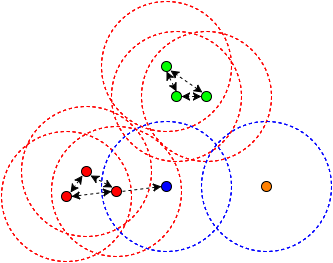
DBSCAN(Density-based spatial clustering of applications of noise)是一种基于密度的聚类方法,仅需要两个参数,能够标记出位于低密度区域的局外点(异常检测中的异常点)。
- 如果一个点 p 在距离 ε 范围内有至少 minPts 个点(包括自己),则这个点被称为核心点,那些 ε 范围内的则被称为由 p 直接可达的。同时定义,没有任何点是由非核心点直接可达的。- 如果存在一条道路 p1, ..., pn ,有 p1 = p和pn = q, 且每个 pi+1 都是由 pi 直接可达的(道路上除了 q 以外所有点都一定是核心点),则称 q 是由 p 可达的。- 所有不由任何点可达的点都被称为局外点。
2. 优缺点
1. 优点:- 相比k-means聚类,dbscan不需要预声明聚类数量- 能找出任意形状的聚类- 对异常数据不敏感2. 缺点:- 对参数的要求较高