线性回归

1. 基本形式

给定数据集：

我们用 来对数据进行拟合，首先需假设线性回归的噪声服从均值为0的高斯分布：

则因变量 y 也服从高斯分布：

因为可通过分别在列向量 和 的末尾添加常数 和 ，所以这里我们简记为 ：

其中：


再令：

2. 最小二乘法求解

基于均方误差最小化来进行模型求解的方法称为“最小二乘法”，此时损失函数：

展开得：

令：

可得


所以线性回归模型为

3. 正则化

在实际应用时，如果样本容量不远大于样本的特征纬度，很可能造成过拟合，解决过拟合主要有以下三种方式：

• 增加数据
  
• 特征选择（降维）
  
• 正则化（regularization）
  

正则化是在损失函数中加入惩罚项，控制参数的幅度，提高模型的稳定性，减轻模型的过拟合。正则化分为L1正则化和L2正则化。

1）L1正则化

又名Lasso，此时损失函数为

求解损失函数的过程可以画出等值线，同时L1正则化的函数也可以在二维平面画出来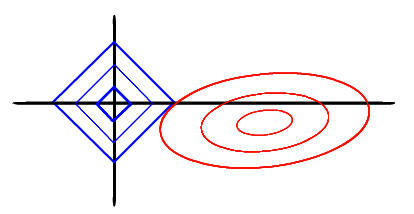

图中的椭圆等高线越接近其中心（越小），模型就越好的拟合现有的数据集，加入正则化项后的解必须是菱形与椭圆的交点，因此新的损失函数的解要在平方误差项与正则化项之间折中，所以椭圆又必须向着坐标轴的原点适当增大，对现有数据集的拟合程度降低，同时也减轻了过拟合。

2）L2正则化

又名Ridge、岭回归，此时损失函数为

同样的得到图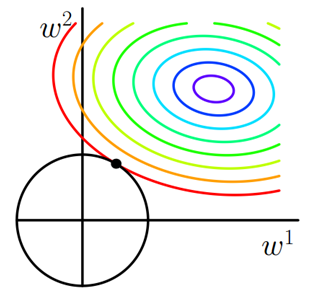

同样的，加入正则化项后的解必须是菱形与椭圆的交点，因此新的损失函数的解要在平方误差项与正则化项之间折中，所以椭圆又必须向着坐标轴的原点适当增大，对现有数据集的拟合程度降低，同时也减轻了过拟合。

3）Lasso与Ridge的选择

• Lasso的优良性质是能产生稀疏性，采用Lasso正则化时，平方误差项与正则项的解常在坐标轴上，导致 中许多项变成0，从而增强了模型的繁华能力。适用于数据的维度较高时的情况。
  
• Ridge主要使模型的解偏向范数较小的 ，通过限制范数的大小实现对模型空间的限制，从而实现减轻过拟合的目的。但是Ridge不具有产生稀疏解的能力（虽然系数变小，但仍不为0），从计算量来说并没有得到改观。适用于数据的维度不高、不需要考虑计算量时的情况。