在学生时期，对于角度制的引入我能非常自然的接受，但后来又引入了弧度制，让我一脸懵逼。为什么有了角度还要引入弧度？为什么角度与弧度能互相转换，它们是一个东西吗？这两个问题一直困扰我很多年，直到今日复习微积分时再度出现。

角度的出现

引用知乎：https://www.zhihu.com/question/21480398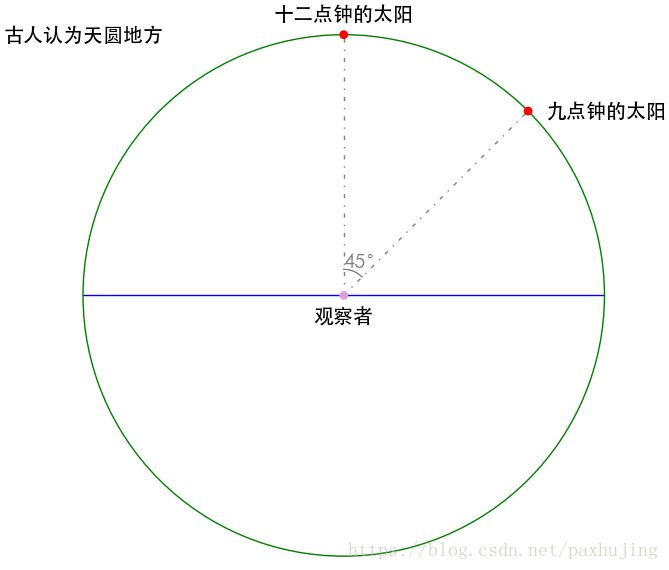

角度的出现，是源于对圆周运动的观察。古人经过长时间的观察发现，地球围绕太阳公转。随着地球的公转，人们在特定的时间看到特定的星座，并得出一个循环周期为360天的规律，也就是一年（虽然后来发现一年实际为365天，但因为360天早已成为习惯且方便计算，所以保留下来）。所以圆被分为360等分。
将圆分为360等分，每一份的夹角为1度，这种度量角大小的方式十分自然，很容易被人接受。那么为什么引入弧度制呢？

弧度制的出现

弧度是从圆周运动的进行者的角度来看待圆周运动的。
之前说过，古人认为天圆地方，人们的旅行都被视为直线运动。可事实上，地球是圆的，随着人类社会的活动，大家越来越认识到传统意义上的直线在地球表面不复存在，必须重新定义直线的含义。弧度也就是在这样的环境下开始发扬光大：

弧度可以把圆周运动转为直线运动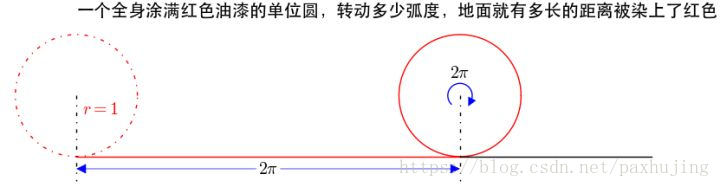


利用弧度也就大大简化了各种与位置、速度有关的计算。

我的理解

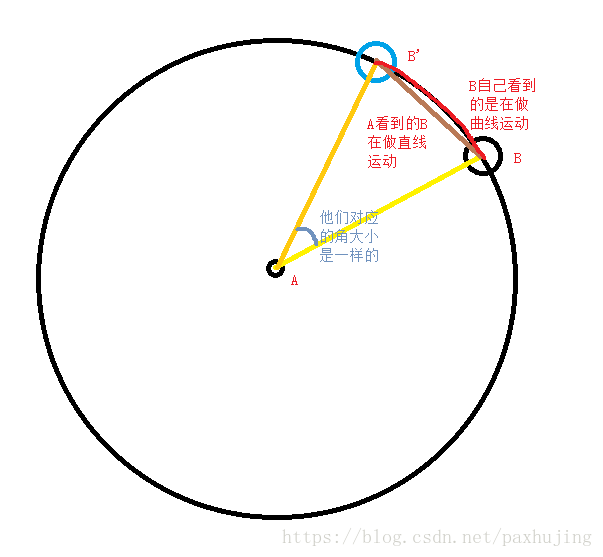
角度与弧度都是对角大小的一种度量方式，只是对同一事物观察的角度不同而有了不同的称呼。它们的区别在于角度以观察者的视角（圆心），将圆周运动视为直线运动；弧度以运动者的视角（周长），将圆周运动视为曲线运动。
假设有两个人A与B，A站在圆心，B站在离r距离的位置，并且B始终要保持在A的视线内。
角度：A站在原地不动，视线转一圈，B始终跟随A的视线移动。在A看来B始终是从一个点直线移动到另一点。这样转一圈360°，将其分为360份，每一份1°。A每转1°，B就从一点直线移动的另一点，也就是说B移动的这一段直线距离对应的A转动的角度大小1°。
弧度：A站在原地不动，B围绕A转一圈。在B看来，自己做的是曲线运动，因为圆周是曲线，围绕A转一圈的距离是2πr，将一圈分为360份，每一份的距离是πr/180。所以B每移动πr/180的距离，A就旋转1°。如果A与B的距离为1（即单位圆），那么B每移动π/180的弧长（即1弧度），A就旋转1°。
在A看来，自己转1°，B就移动一段直线距离。在B看来，A转1°，自己就移动一段曲线距离。所以，对于同样大小的角，A用直线来描述，B用曲线来描述。


所以：1°=(π/180)弧度；1弧度=(180/π)度