9. 再谈正态分布的运用
正态分布计算
加法
离散概率分布:
%3DE(X)%2BE(Y)#card=math&code=E%28X%2BY%29%3DE%28X%29%2BE%28Y%29)
%3DVar(X)%2BVar(Y)#card=math&code=Var%28X%2BY%29%3DVar%28X%29%2BVar%28Y%29)
**已知 ~
#card=math&code=N%28%5Cmu_x%2C%5Csigma_x%5E2%29) 且
#card=math&code=N%28%5Cmu%2C%5Csigma%5E2%29)==
其中 ,

变量相加后,变异性( )增加,图形变扁,总面积仍小于1
减法
减法同加法相同
线性变化
线性变化描述了数据的基本变化
~
#card=math&code=N%28a%5Cmu%2Bb%2Ca%5E2%5Csigma%5E2%29)
独立观测结果
独立观察结果描述你有多少数值
~
#card=math&code=N%28n%5Cmu%2Cn%5Csigma%5E2%29)
注: 若一位成年人的体重分布为X~
#card=math&code=N%28180%2C625%29),计算4位成年人的综合体重概率分布
- 线性变化
若使用4X,实际描述的是一位成年人体重放大4倍后的效果- 独立观测
,
,
,
是X的独立观察结果
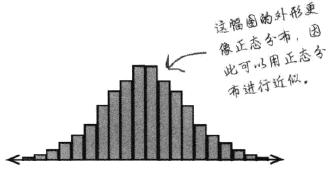
二项分布近似替代
替代条件
一般情况,当np和nq双双大于5时(n为次数,p为成功概率,q=1-p),可以用正态分布近似替代二项分布。
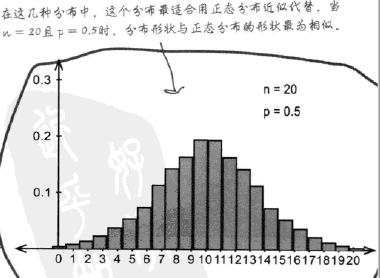
替代场景
求解均值和方差
直接从二项分布的发哦均值与方差方便计算概率:
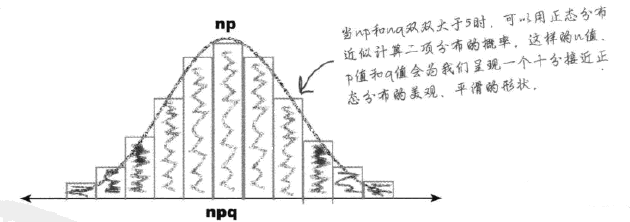
部分近似条件可能为np>10,nq>10
误差修正
- 二项分布 P(X<6)
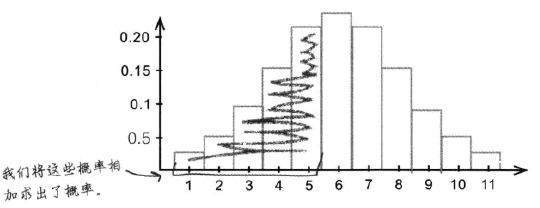
- 正态分布 P(X<6)
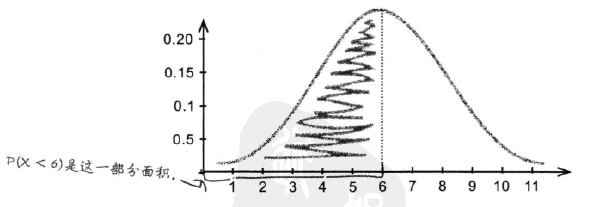
- 两者存在误差
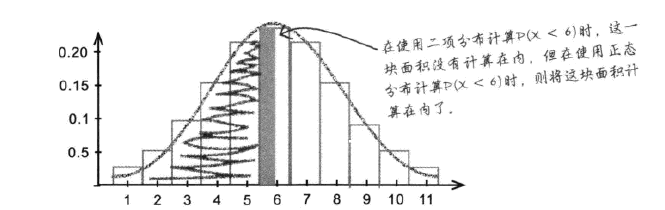
误差原因:离散数值为6,转化连续标度,考虑所有取整后等于6的数,即要考虑从5.5-6.5的数字范围.
计算P(X<6)应该计算P(X<5.5),这种调整称为连续性修正
| 所求二项分布 | 连续性修正后 |
|---|---|
| P(X≤a) | P(X<a+0.5) |
| P(X≥a) | P(X>a-0.5) |
| P(a≤X≤b) | P(a-0.5<X<b+0.5) |
泊松分布近似替代
~
#card=math&code=Po%28%5Clambda%20%29)
- 当
>15,可以用X~
#card=math&code=N%28%5Clambda%2C%5Clambda%29) 近似替代
如果用正态分布近似替代泊松分布,为保证结果正确,需要进行连续性修正
总结


