SVM原理

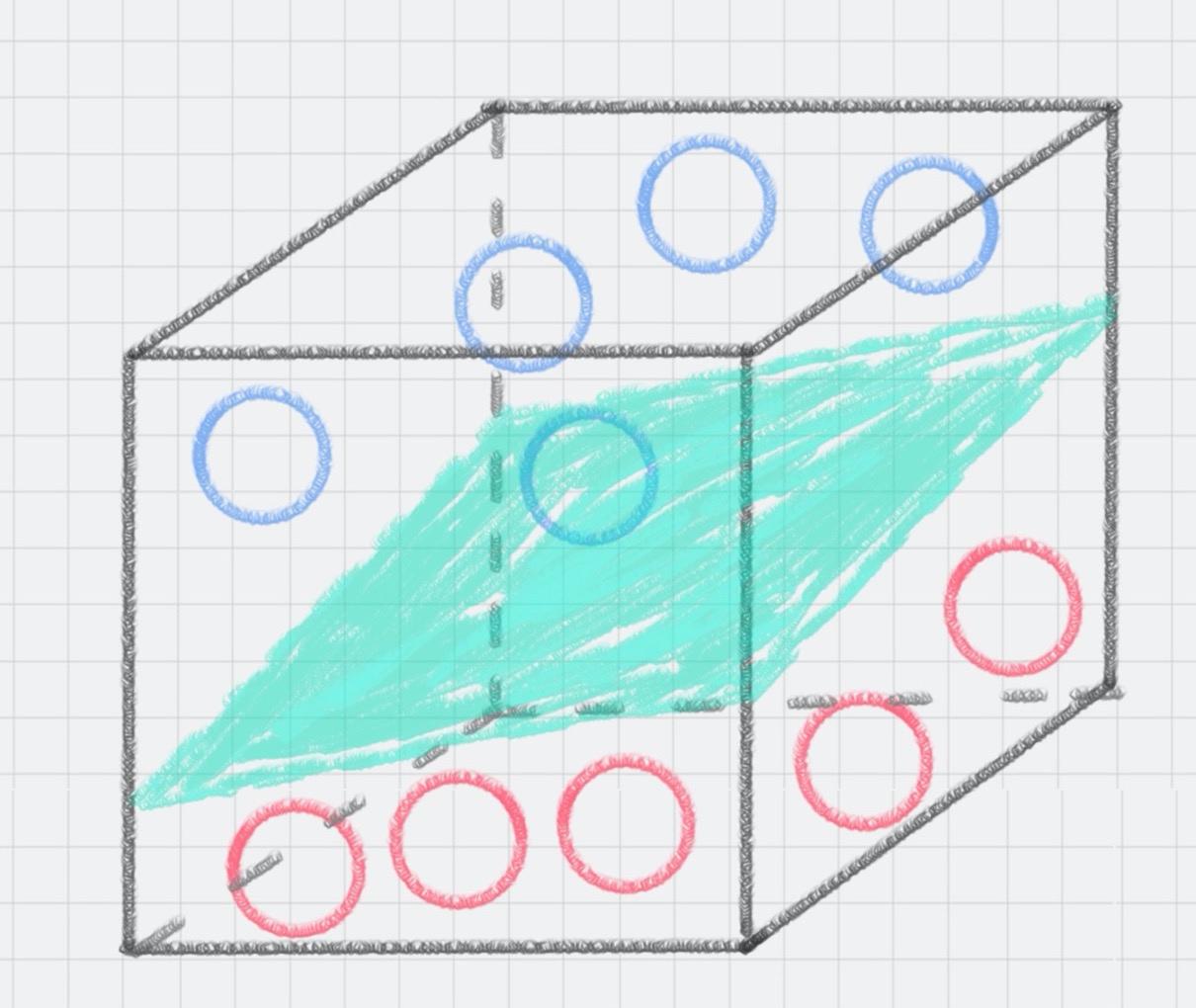
4. 支撑向量机SVM - 图1

这个平面，我们就叫做超平面。SVM 计算的过程就是帮我们找到那个超平面的过程，这个超平面就是我们的 SVM 分类器。

二维空间为例子

4. 支撑向量机SVM - 图2

  • 样本训练点分布在平面直角坐标系内，找到直线4. 支撑向量机SVM - 图3恰好将样本分为两类。
  • 点4. 支撑向量机SVM - 图4#card=math&code=%28x_0%2Cy_0%29)到直线的距离为4. 支撑向量机SVM - 图5
  • 使得最小距离最大化

分类间隔：保证决策面不变，分类不产生错误情况下，移动决策面C产生最优的决策面（拥有最大间隔决策面）

推广

4. 支撑向量机SVM - 图6%3Dw%5ETx%2Bb%20w%2Cx%5Cin%20R%5En%0A#card=math&code=g%28x%29%3Dw%5ETx%2Bb%20w%2Cx%5Cin%20R%5En%0A)

  • w,x均为n维空间的向量
  • w为法向量，垂直与平面直线所代表的向量，决定超平面的方向

支持向量为离超平面最近的样本点
此时点到超平面的距离公式：

4. 支撑向量机SVM - 图7

  • 4. 支撑向量机SVM - 图8 超平面范数（欧式距离）

最大间隔的优化模型

我们的目标就是找出所有分类间隔中最大的那个值对应的超平面。在数学上，这是一个凸优化问题（凸优化就是关于求凸集中的凸函数最小化的问题，这里不具体展开）。通过凸优化问题，最后可以求出最优的 w 和 b，也就是我们想要找的最优超平面。中间求解的过程会用到拉格朗日乘子，和 KKT（Karush-Kuhn-Tucker）条件。数学公式比较多，这里不进行展开。

硬间隔、软间隔和非线性 SVM

SVM分类

  • 硬间隔支持向量机
    硬间隔指的就是完全分类准确，不能存在分类错误的情况。
  • 软间隔支持向量机
    就是允许一定量的样本分类错误。
  • 非线性支持向量机。
    样本集是个非线性的数据
    需要引入：核函数

核函数它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。
所以在非线性 SVM 中，核函数的选择就是影响 SVM 最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid 核，或者是这些核函数的组合。这些函数的区别在于映射方式的不同。通过这些核函数，我们就可以把样本空间投射到新的高维空间中。

用 SVM 解决多分类问题

SVM 本身是一个二值分类器，最初是为二分类问题设计的，也就是回答 Yes 或者是 No。而实际上我们要解决的问题，可能是多分类的情况，比如对文本进行分类，或者对图像进行识别。

针对这种情况，我们可以将多个二分类器组合起来形成一个多分类器，常见的方法有“一对多法”和“一对一法”两种。

  1. 一对多法

假设我们要把物体分成 A、B、C、D 四种分类，那么我们可以先把其中的一类作为分类 1，其他类统一归为分类 2。这样我们可以构造 4 种 SVM，分别为以下的情况：

（1）样本 A 作为正集，B，C，D 作为负集；

（2）样本 B 作为正集，A，C，D 作为负集；

（3）样本 C 作为正集，A，B，D 作为负集；

（4）样本 D 作为正集，A，B，C 作为负集。

这种方法，针对 K 个分类，需要训练 K 个分类器，分类速度较快，但训练速度较慢，因为每个分类器都需要对全部样本进行训练，而且负样本数量远大于正样本数量，会造成样本不对称的情况，而且当增加新的分类，比如第 K+1 类时，需要重新对分类器进行构造。

  1. 一对一法

一对一法的初衷是想在训练的时候更加灵活。我们可以在任意两类样本之间构造一个 SVM，这样针对 K 类的样本，就会有 C(k,2) 类分类器。

比如我们想要划分 A、B、C 三个类，可以构造 3 个分类器：

（1）分类器 1：A、B；

（2）分类器 2：A、C；

（3）分类器 3：B、C。

当对一个未知样本进行分类时，每一个分类器都会有一个分类结果，即为 1 票，最终得票最多的类别就是整个未知样本的类别。

这样做的好处是，如果新增一类，不需要重新训练所有的 SVM，只需要训练和新增这一类样本的分类器。而且这种方式在训练单个 SVM 模型的时候，训练速度快。

但这种方法的不足在于，分类器的个数与 K 的平方成正比，所以当 K 较大时，训练和测试的时间会比较慢。

sklearn实现

  1. from sklearn import svm

SVM 既可以做回归，也可以做分类器。

  • 做回归的时候，我们可以使用 SVR 或 LinearSVR。SVR 的英文是 Support Vector Regression。
  • 做分类器的时候，我们使用的是 SVC 或者 LinearSVC。SVC 的英文是 Support Vector Classification。
  1. model = svm.SVC(kernel=‘rbf’, C=1.0, gamma=‘auto’)

这里有三个重要的参数 kernel、C 和 gamma。

  • kernel 代表核函数的选择。
    • linear：线性核函数。是在数据线性可分的情况下使用的，运算速度快，效果好。不足在于它不能处理线性不可分的数据。
    • poly：多项式核函数。多项式核函数可以将数据从低维空间映射到高维空间，但参数比较多，计算量大。
    • rbf：高斯核函数（默认）。同样可以将样本映射到高维空间，但相比于多项式核函数来说所需的参数比较少，通常性能不错，所以是默认使用的核函数。
    • sigmoid：sigmoid 核函数。sigmoid 经常用在神经网络的映射中。因此当选用 sigmoid 核函数时，SVM 实现的是多层神经网络。
      除了第一种线性核函数外，其余 3 种都可以处理线性不可分的数据。
  • C 代表目标函数的惩罚系数，惩罚系数指的是分错样本时的惩罚程度，默认情况下为 1.0。
    • 当 C 越大的时候，分类器的准确性越高，但同样容错率会越低，泛化能力会变差。相反，C 越小，泛化能力越强，但是准确性会降低。
  • gamma 代表核函数的系数，默认为样本特征数的倒数，即 gamma = 1 / n_features。