8. 回归

回归

回归就是需要找到一个能够很好地将某些特征映射到其他特征的函数。依赖特征称为因变量，独立特征称为自变量。

通常用y表示因变量，x表示自变量。如果有两个或者多个自变量，可以用向量#card=math&code=x%3D%28x_1%2C%20%E2%80%A6%2C%20x_r%29&height=20&width=116)表示。

回归的作用

• 回归被用来回答某些现象是否会对其他现象产生影响，或者说，几个变量之间是否存在关联。例
• 用新的自变量数据集去预测因变量时，回归也是非常有用的。

线性回归的原理

线性回归是被广泛使用的回归方法中比较重要的一种。它是最基础也是最简单的回归方法。它的主要优点是易懂。

在对一组自变量¥x=(x_1,…,x_r)$和因变量y进行回归时，我们假设y与x的关系：

• 这个方程叫做回归方程。可以很好地捕获自变量与因变量的依赖关系。
• 是回归系数,表示用于预测的权重
• 是随机误差

对于每一次观测i=1,…,n，回归函数f()应该要足够接近实际观测的因变量值，其中yi与f(xi)的差值称为残差。回归是为了找到最优权重并用于预测，而残差最小的时候说明回归函数f()与实际观测的yi是最接近的，此时对应的权重便是最优权重b=()。

最小二乘法OLS

通常使用最小化残差平方和的方法来计算最优权重，即最小化)%5E2#card=math&code=SSR%3D%5Csum_%7Bi%3D1%7D%5En%28y_i-f%28x_i%29%29%5E2&height=49&width=174)。这种方法叫做最小二乘法OLS。

评价回归模型

决定系数R2，用来说明实际观测值yi中有多大程度可以由回归函数f(x)解释。R2越大，两者拟合程度越高，意味着观测值数据组可以很好的契合回归函数f(x)。

R2=1时，即SSR=0，称作完全拟合

单变量线性回归

单变量线性回归是线性回归中最简单的一种情形，即回归模型中只有一个自变量x=x1。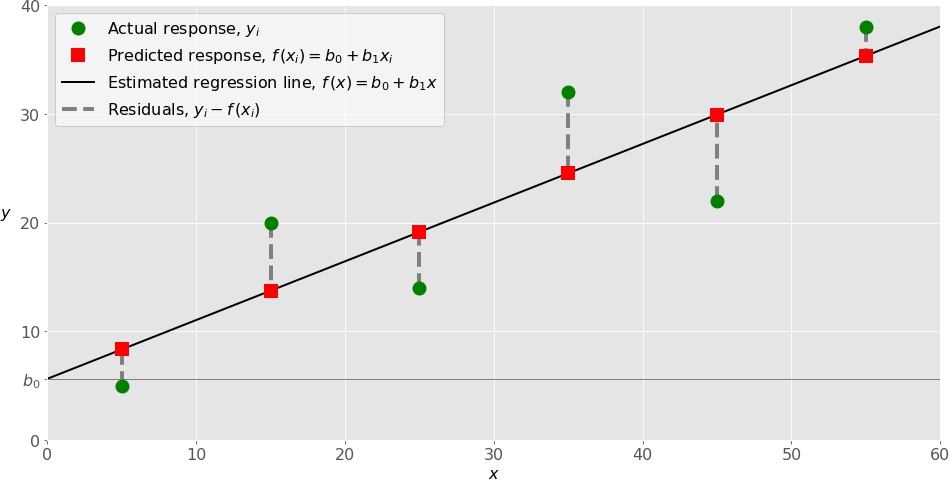

多变量线性回归

假如仅有两个自变量，回归函数可以写成%3Db_0%2Bb_1x_1%2Bb_2x_2#card=math&code=f%28x_1%2Cx_2%29%3Db_0%2Bb_1x_1%2Bb_2x_2&height=20&width=206)

多项式回归

可以将多项式回归视为线性回归的一般情形。自变量与因变量的多项式依赖关系可以通过回归得到多项式回归函数。

回归函数f中，除了包含线性部分如，还可以加入非线性部分如等等。

只需要将高阶项如x2视为因变量，多项式回归与普通的线性回归是一样的。

欠拟合和过拟合

阶数的选择并没有明确的规则。它需要视情况而定。但是，在选择阶数的时候，需要关注两个问题：欠拟合与过拟合。

欠拟合

当模型无法准确的捕获数据之间的依赖关系时导致欠拟合，这通常是由于模型过于简单导致的。欠拟合的模型在用现有数据进行回归时会有较低的决定系数R2，同时它的预测能力也不足。

过拟合

当数据和随机波动性都拟合到模型中时会导致过拟合。换种说法，就是模型和现有数据契合程度过高了。高度复杂的模型一般都有很多自变量，这通常容易导致模型过拟合。将现有数据拟合这种模型的时候一般会有很高的决定系数R2。但是在使用新数据时，模型可能会表现出很弱的预测能力和低决定系数R2。

在Python中实现线性回归

• numpy是一款基础Python包，它可以在单维和多维数组上进行高效的操作。它还提供很多数值计算方法，同时也是开源库。
• scikit-learn是一个被大量用户用于机器学习的Python库，该库是基于numpy和其他库建立的。它可以执行数据预处理，降维，回归，分类和聚类等功能。和numpy一样，scikit-learn也是开源的。

可以在scikit-learn官网上查看Generalized Linear Models页面了解更多关于线性模型的内容以进一步了解该库的原理。

• statsmodels库可以实现一些在做线性回归时scikit-learn中没有的功能。它也是一个不错的Python库，主要用于统计模型的估计，模型的测试等等。同时它也是开源的。

基于sklearn的单变量线性回归

这里从最简单的单变量线性回归开始，手把手教你在Python中做线性回归模型，整个过程大致分五个基本步骤：

Step 1：导入相关库和类

import pandas as pd
import numpy as np
import tushare as ts
from sklearn.linear_model import LinearRegression#提供了执行线性回归的相关功能

Step 2：读取数据

经过简单处理，现在有了自变量x和因变量y。需要注意的是，sklearn.linear_model.LinearRegression类需要传入的自变量是一组二维数组结构，因此可以通过numpy的.reshape()方法将一维数组变更为二维数组，另一种方法就是使用pandas的DataFrame格式。

Step 3：建立模型并拟合数据

model = LinearRegression()

• fit_intercept：布尔值，默认为True。True为需要计算截距b0，False为不需要截距，即b0=0。
• normalize：布尔值，默认为False。参数作用是将数据标准化，False表示不做标准化处理。
• copy_x：布尔值，默认为True。True为保留x数组，False为覆盖原有的x数组。
• n_jobs：整型或者None，默认为None。这个参数用于决定并行计算线程数。None表示单线程，-1表示使用所有线程。

模型建立以后，首先需要在模型上调用.fit()方法：

model.fit(x, y)

Step 4：输出结果

数据拟合模型后，可以输出结果看看模型是否满意，以及是否可以合理的解释数据的趋势或者依赖关系。

可以通过调用.score()方法来获取model的R2：

model = LinearRegression().fit(x, y)
r_sq = model.score(x, y)
print(r_sq)

同时，也可以通过调取model的.intercept_和.coef_属性获取截距b0和斜率b1：

print('intercept:', model.intercept_)
print('slope:', model.coef_)

需要注意的是，.intercept_是一个numpy.float64数值，而.coef_是一个numpy.array数组。

Step 5：模型预测

要获得预测结果，可以使用.predict()方法

基于sklearn的多变量线性回归

与上相同

基于sklearn的多项式回归

执行多项式回归步骤与前面也相似，只是需要增加一组经过转换的自变量作为非线性项，如x2。

Step 1：导入相关库和类

除了需要导入pandas和tushare，sklearn.linear_model.LinearRegression外，还需要导入sklearn.preprocessing中的PolynomialFeatures类用来处理非线性项。

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

Step 2：读取数据

Step 3：自变量转换

这个步骤是多项式回归需要执行的步骤。由于多项式回归中有x2项，因此需要将x数组转换成x2并作为新的列。

有很多种转换方式，比如使用numpy中的insert()方法，或者pandas的DataFrame添加x2列。本例中使用的是PolynomialFeatures类：

transformer = PolynomialFeatures(degree=2, include_bias=False)

transformer是PolynomialFeatures类的实例，用于对自变量x进行转换。

• degree：整型，默认为2。用于决定线性回归模型的阶数。
• interaction_only：布尔值，默认为False。如果指定为True，那么就不会有项
• include_bias：布尔值，默认为True。此参数决定是否将截距项添加为回归模型中的一项，即增加一列值为1的列。False表示不添加。

先将自变量x数据传入转换器transformer中：

transformer.fit(x)

传入transformer之后，就可以使用.transform()方法获得转换后的数据x和x2：

x_ = transformer.transform(x)

Step 4：建立模型并拟合数据

model = LinearRegression().fit(x_, y)

【注】模型中第一个参数变为经过处理后的数据x_，而不是原始的自变量x数组。

Step 5：输出结果

Step 6：模型预测