大数据认识

大数据产业生产流程

数据收集、数据存储、数据建模、数据分析、数据变现

大数据人才方向

• 偏重基建与架构的“大数据架构”方向

  （1）架构理论：关键词有高并发、高可用、并行计算、MapReduce、Spark等。

  （2）数据流应用：关键词有Flume、Fluentd、Kafka、ZMQ等。

  （3）存储应用：关键词有HDFS、Ceph等。

  （4）软件应用：关键词有Hive、HBase、Cassandra、PrestoDB等。

  （5）可视化应用，关键词有HightCharts、ECharts、D3、HTML5、CSS3等。

• 偏重建模与分析的“大数据分析”方向。
  （1）数据库应用：关键词有RDBMS、NoSQL、MySQL、Hive、Cassandra等。
  （2）数据加工：关键词有ETL、Python等。
  （3）数据统计：关键词有统计、概率等。
  （4）数据分析：关键词有数据建模、数据挖掘、机器学习、回归分析、聚类、分类、协同过滤等。

• 偏重应用实现的“大数据开发”方向。
  （1）数据库开发：关键词有RDBMS、NoSQL、MySQL、Hive等。
  （2）数据流工具开发：关键词有Flume、Heka、Fluentd、Kafka、ZMQ等。
  （3）数据前端开发：关键词有HightCharts、ECharts、JavaScript、D3、HTML5、CSS3等。
  （4）数据获取开发：关键词有爬虫、分词、自然语言学习、文本分类等。

数据相关名词辨析

• 数据：承载信息的东西
• 信息：用来消除随机不定性的东西
• 算法： 计算机的方法与技巧（ 数据加工的灵魂）
• 数据挖掘
  • 一定量的数据作为研究对象
  • 进行深度的研究、对比、甄别等工作
  • 从中找到规律或知识
• 机器学习：让机器独立或至少半独立地进行相对复杂或者高要求的工作。（帮助人类做一些大规模的数据识别、分拣、规律总结等人类做起来比较花时间的事情。）
• 商业智能BI（Business Intelligence）

通过应用基于事实的支持系统来辅助商业决策的制定。商业智能技术提供使企业迅速分析数据的技术和方法，包括收集、管理和分析数据，将这些数据转化为有用的信息。

排列组合相关

传统概率

如果一个随机试验所包含的单位事件是有限的，且每个单位事件发生的可能性均相等，则这个随机试验叫做拉普拉斯试验，这种条件下的概率模型就叫古典概型。古典概型也叫传统概率

非古典概率

包含的单位事件不是有限的或每个单位事件发生的可能性不均等——非古典概率

排列

从一个较大的（n个）对象群体中取出一定数目（r个）对象进行排序，并得出排序方式总数目。

!%7D#card=math&code=%5EnP_r%3D%5Cfrac%7Bn%21%7D%7B%28n-r%29%21%7D)

• n为对象总数
• 为要计算的对象数目

组合

从n个对象中选取r个对象的选取方式的数目，不考虑所选对象的确切顺序。

!%7D%0A#card=math&code=%5EnC_r%3D%5Cfrac%7Bn%21%7D%7Br%21%28n-r%29%21%7D%0A)

• 数字越大，位置越高
• 另一种表示方式

“概率本身的解释就是对于大量样本分布比例的解释，而不是对单次事件的可能性的解释。我们说扔硬”

统计分布

均值

• 平均数的一般量度
• 将所有数字加起来，除以数字个数

1. 求和
   
2. 平均值
   

频数均值

• 表示每个数字乘以其频数，然后相加
• 表示每个数频数相加

中位数

当偏斜数据和异常值使均值产生误导时,我们就需要用其他方式表示典型值。我们可以取中间值，中位数永近处于中间,它是个中间值。

求中位数三步法：

1. 按顺序排列数字:从最小値排列到最大値。
2. 如果奇数个数,则中位数为位于中间的数値。位置为
3. 如果偶数个数,将两个中间数相加,然后除以2。位置为

众数

• 数据集中的数
• 出现最频繁的数值
• 可能不止一个（有个众数：双峰数据）
• 既能用于数值数据，又能用于类别数据

众数的计算

• 不同类别的数值或类别找出
• 列出频数
• 找出最值

方差

量度数据变异性的方法

%5E2%7D%7Bn%7D#card=math&code=%E6%96%B9%E5%B7%AE%3D%5Cfrac%7B%5Csum%28x-%5Cmu%29%5E2%7D%7Bn%7D)

方差是数据值与均值的距离的平方数的平均值

快速计算方法

标准差

不用距离的平方来指出分散性

%5E2%7D%7Bn%7D%7D#card=math&code=%5Csigma%3D%5Csqrt%7B%E6%96%B9%E5%B7%AE%7D%3D%5Csqrt%7B%5Cfrac%7B%5Csum%28x-%5Cmu%29%5E2%7D%7Bn%7D%7D)

标准分

特定数据值的标准分

为数据所在数据集的均值，标准差

曼哈顿距离（Manhattan Distance）

在二维空间中，两个点（实际上就是二维向量）#card=math&code=x%28x_1%2Cx_2%29)与#card=math&code=y%28y_1%2Cy_2%29) 间的曼哈顿距离是：

%3D%7Cx_1-y_1%7C%2B%7Cx_2-y_2%7C%0A#card=math&code=MD%28x%2Cy%29%3D%7Cx_1-y_1%7C%2B%7Cx_2-y_2%7C%0A)

推广到n维空间，曼哈顿距离的计算公式为：

%3D%5Csum%7Bi%3D1%7D%5En%7Cx_i-y_i%7C%0A#card=math&code=MD%28x%2Cy%29%3D%5Csum%7Bi%3D1%7D%5En%7Cx_i-y_i%7C%0A)

• n表示向量维度
• 表示第一个向量的第维元素的值
• 表示第二个向量的第维元素的值

欧氏距离（Euclidean Distance）

欧几里得距离。欧氏距离是一个常用的距离定义，指在 n 维空间中两个点之间的真实距离，在二维空间中，两个点#card=math&code=x%28x_1%2Cx_2%29)与#card=math&code=y%28y_1%2Cy_2%29) 间的欧氏距离是：

%3D%5Csqrt%7B(x_1-y_1)%5E2%2B(x_2-y_2)%5E2%7D%0A#card=math&code=ED%28x%2Cy%29%3D%5Csqrt%7B%28x_1-y_1%29%5E2%2B%28x_2-y_2%29%5E2%7D%0A)

推广到 n 维空间，欧氏距离的计算公式为：

%3D%5Csqrt%7B%5Csum%7Bi%3D1%7D%5En%7B(x_i-y_i)%5E2%7D%7D%0A#card=math&code=ED%28x%2Cy%29%3D%5Csqrt%7B%5Csum%7Bi%3D1%7D%5En%7B%28x_i-y_i%29%5E2%7D%7D%0A)

切比雪夫距离（Chebyshev Distance）

在二维空间，两个点#card=math&code=x%28x_1%2Cx_2%29)与#card=math&code=y%28y_1%2Cy_2%29) 间的切比雪夫距离：

%3Dmax(%7Cx_1-y_1%7C%2C%7Cx_2-y_2%7C)%0A#card=math&code=CD%28x%2Cy%29%3Dmax%28%7Cx_1-y_1%7C%2C%7Cx_2-y_2%7C%29%0A)

推广到 n 维空间，切比雪夫距离的计算公式为：

%3Darg%20max%7Bi%3D1%7D%5En%7Cx_i-y_i%7C%0A#card=math&code=CD%28x%2Cy%29%3Darg%20max%7Bi%3D1%7D%5En%7Cx_i-y_i%7C%0A)

• )#card=math&code=argmax%28f%28x%29%29)是使得 f(x)取得最大值所对应的变量点x(或x的集合)

闵氏距离

上述三种距离，都可以用一种通用的形式表示，那就是闵可夫斯基距离(闵氏距离)

在二维空间中，两个点#card=math&code=x%28x_1%2Cx_2%29)与#card=math&code=y%28y_1%2Cy_2%29) 间的闵氏距离是：

%3D%5Csqrt%5Bp%5D%7B%7Cx_1-y_1%7C%5Ep%2B%7Cx_2-y_2%7C%5Ep%7D%0A#card=math&code=MKC%28x%2Cy%29%3D%5Csqrt%5Bp%5D%7B%7Cx_1-y_1%7C%5Ep%2B%7Cx_2-y_2%7C%5Ep%7D%0A)

两个n维变量#card=math&code=x%28x_1%2Cx_2%2Cx_3%2C%5Cdots%2Cx_n%29)与#card=math&code=y%28y_1%2Cy_2%2Cy_3%2C%5Cdots%2Cy_n%29)间的闵氏距离的定义为：

%3D%5Csqrt%5Bp%5D%7B%5Csum%7Bi%3D1%7D%5En%7Cx_i-y_i%7C%5Ep%7D%0A#card=math&code=MKC%28x%2Cy%29%3D%5Csqrt%5Bp%5D%7B%5Csum%7Bi%3D1%7D%5En%7Cx_i-y_i%7C%5Ep%7D%0A)

为变参数

• =1，曼哈顿距离
• =2，欧式距离
• ,切比雪夫距离(当,最大的占全部权重)

距离可以描述不同向量在向量空间中的差异，所以可以用于描述向量所代表的事物之差异（或相似）程度。

同比环比

同比：“与相邻时段的同一时期相比”

环比：与上一个报告期进行比较

抽样

一种非常好的了解大量样本空间分布情况的方法，样本越大则抽样带来的成本减少的收益就越明显。

概率分布

特殊的概率分布，固定的模式，方便计算概率，期望，方差

几何分布

• #card=math&code=P%28X%3Dx%29)表示x能取概率分布的任何值
• #card=math&code=P%28X%3Dr%29)表示x等于特定值r
• 即x可以取任何值，包括固定值r

公式

%3Dq%5E%7Br-1%7Dp#card=math&code=P%28X%3Dr%29%3Dq%5E%7Br-1%7Dp)

• p代表成功的概率
• q代表失败的概率，q=1-p

表示取得第r次首次成功所需要进行的试验次数的概率

条件

• 一系列相互独立试验
• 均有成功，失败的可能，且单次概率相同
• 求得为取得第一次成功所需要进行多少次试验（用变量X表示）

图像特点

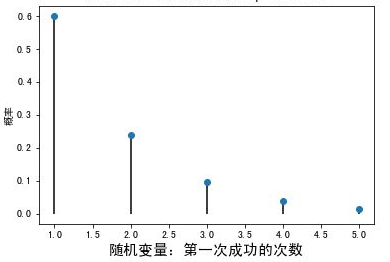
• 当r=1时，P（X=r）达到最大值，随着r的增加，P（X=r）逐渐减少
• 任何几何分布的众数都是1，因为1时，具有的概率最大
• 第一次尝试，可能性最大

不等式几何分布

%3Dq%5Er%0A#card=math&code=P%28X%3Er%29%3Dq%5Er%0A)

• X表示为取得第一次成功所需要进行多少次试验
• r表示试验进行的次数

%3D1-q%5Er%0A#card=math&code=P%28X%E2%89%A4r%29%3D1-q%5Er%0A)

• 表示为了取得一次成功需要尝试r次或r次的以下概率
• %2BP(X%3Er)%3D1#card=math&code=P%28X%E2%89%A4r%29%2BP%28X%3Er%29%3D1)

如果一个变量X的概率符合几何分布，单次成功的概率为p，写作

~#card=math&code=Geo%28p%29)

期望

X~#card=math&code=Geo%280.2%29)时，E(X)可以通过#card=math&code=%5Csum%20xP%28X%3Dx%29)进行计算：

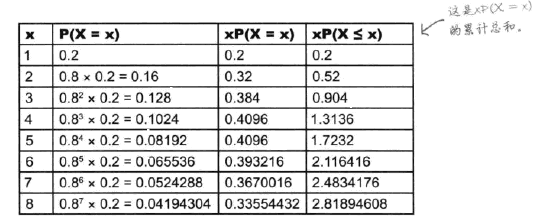
#card=math&code=%5Csum%20xP%28X%3Dx%29)图

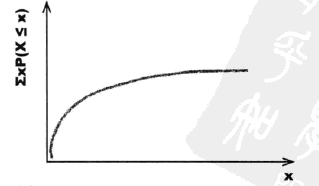
%3D%5Cfrac%7B1%7D%7Bp%7D#card=math&code=E%28X%29%3D%5Cfrac%7B1%7D%7Bp%7D)

期望等于1除以成功概率

方差

X~#card=math&code=Geo%280.2%29)时，E(X)可以通过#card=math&code=x%5E2%20P%28X%3Dx%29)进行计算：

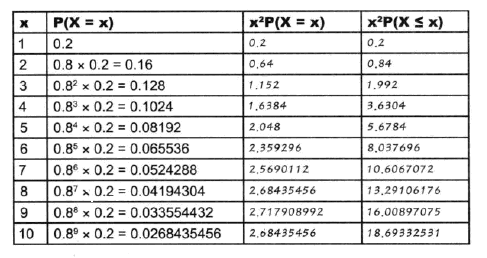
#card=math&code=x%5E2%20P%28X%3Dx%29)图

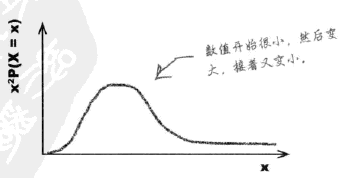
%3DE(X%5E2)-E%5E2(X)%3Dx%5E2%20P(X%3Dx)-E%5E2(X)#card=math&code=Var%28X%29%3DE%28X%5E2%29-E%5E2%28X%29%3Dx%5E2%20P%28X%3Dx%29-E%5E2%28X%29),得到方差分布图

如果X~#card=math&code=Gep%28p%29)，则%3D%5Cfrac%7Bq%7D%7Bp%5E2%7D#card=math&code=Var%28X%29%3D%5Cfrac%7Bq%7D%7Bp%5E2%7D)

二项式分布

公式

%3D%5EnC_rp%5Erq%5E%7Bn-r%7D#card=math&code=P%28X%3Dr%29%3D%5EnC_r%2Ap%5Er%2Aq%5E%7Bn-r%7D)

其中!%7D#card=math&code=%5EnC_r%3D%5Cfrac%7Bn%21%7D%7Br%21%28n-r%29%21%7D)

每道题答对的概率是p 答错的概率是q=1-p

条件

• 独立试验
• 均有成功，失败的可能，且单次概率相同
• 试验次数有限

p是每一次试验的成功概率，n是试验次数。写作：X~#card=math&code=B%28n%2Cp%29)

图像

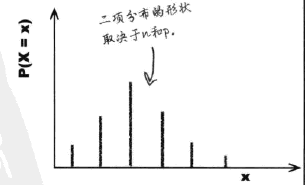
期望

%3Dnp#card=math&code=E%28X%29%3Dnp)

方差

%3Dnpq#card=math&code=Var%28X%29%3Dnpq)

泊松分布

条件

• 单独时间在给定区间（时间或者空间）内随机、独立地发生
• 已知改区间的时间平均发生次数（发生率）通常用(lambda)表示

每个区间内平均发生次，或者说发生率为，写作X~#card=math&code=Po%28%5Clambda%29)

公式

%3D%5Cfrac%7Be%5E%7B-%5Clambda%7D%5Clambda%20%5Er%7D%7Br!%7D#card=math&code=P%28X%3Dr%29%3D%5Cfrac%7Be%5E%7B-%5Clambda%7D%5Clambda%20%5Er%7D%7Br%21%7D)

• 是数学的常数，一般为2.718

期望

%3D%5Clambda#card=math&code=E%28X%29%3D%5Clambda)

方差

%3D%5Clambda#card=math&code=Var%28X%29%3D%5Clambda)

图形

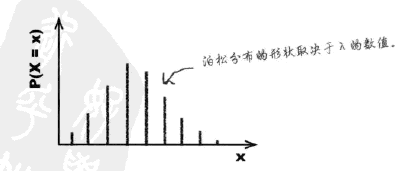
• $\lambda $值小，分布向右
• $\lambda $值大，分布逐渐变得对称
• $\lambda \lambda \lambda -1$

x+y泊松分布

如果X和Y是独立随机变量，则：

%3DP(X)%2BP(Y)#card=math&code=P%28X%2BY%29%3DP%28X%29%2BP%28Y%29)

%3DE(X)%2BE(Y)#card=math&code=E%28X%2BY%29%3DE%28X%29%2BE%28Y%29)

即如果X~ #card=math&code=Po%28%5Clambda_x%29)且Y~ #card=math&code=Po%28%5Clambda_y%29)，则：

X+Y~ #card=math&code=Po%28%5Clambda_x%2B%5Clambda_y%29)

如果X和Y都复合泊松分布，则X+Y也符合泊松分布

使用二项式分布替代

当n很大且p很小时，可以用X~#card=math&code=Po%28np%29) 近似代替X~#card=math&code=B%28n%2Cp%29).

正态分布

连续数据的理想模型

• 钟形曲线，曲线对称，中央部位的概率密度最大。
• 越是偏离均值 ， 概率密度减小。
• 均值和中位数均位于中央 ， 具有最大概率密度。

通过参数和进行定义。 指出曲线的中央位置， 指出分散性。

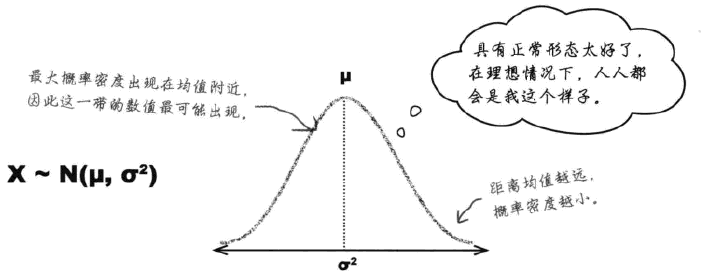
• 越大，正态分布越扁平
• 概率密度无限接近于但不等于0

正态概率计算

• 求介于a和b之间的概率（借助概率表）

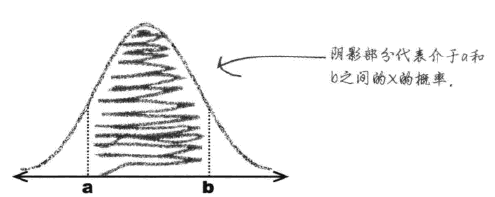
1. 确定概率分布与范围
   • 计算均值,标准差
   • 需要求出那一部分概率
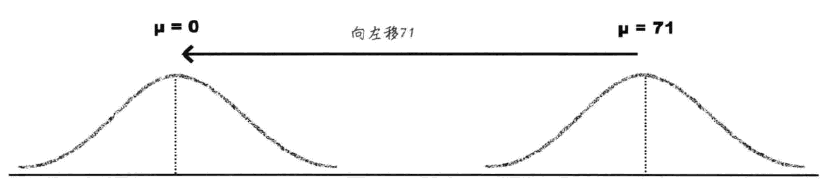
2. 标准化#card=math&code=N%280%2C1%29)
   • 移动均值

• 收窄

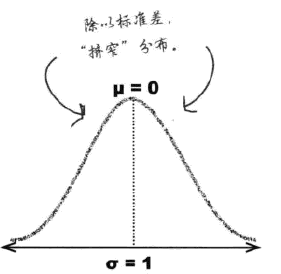
概率表仅给出N(0,1)分布的概率，需要进行标准化

单位为比特（bit）

• 信源有m种消息
• m种情况产生的概率是均等的

极少事件发生信息量计算

%3D-log_2%20P%0A#card=math&code=H%28X_i%29%3D-log_2%20P%0A)

• 一个发生的事件
• P表示这个事件发生的先验概率

香农公式 %0A#card=math&code=C%3DB%2Alog_2%281%2B%5Cfrac%7BS%7D%7BN%7D%29%0A) 单位：bps

• “B是码元速率的极限值（奈奎斯特指出，B=2H，H为信道带宽，单位为Baud）
• S是信号功率（瓦）
• N是噪声功率（瓦）

信息熵

信息的杂乱程度的量化描述。

%3D-%5Csum_i%5Enp(x_i)log_2P(x_i)%2Ci%3D1%2C2%2C%5Cdots%2Cn%0A#card=math&code=H%28x%29%3D-%5Csum_i%5Enp%28x_i%29log_2P%28x_i%29%2Ci%3D1%2C2%2C%5Cdots%2Cn%0A)

x可以当成一个向量，就是若干个产生的概率乘以该可能性的信息量，然后各项做加和

线性代数

向量和向量空间
###变量的分类
标量（Scalar）

它只是一个单独的数字，而且不能表示方向。从计算机数据结构的角度来看，标量就是编程中最基本的变量。

向量（Vector）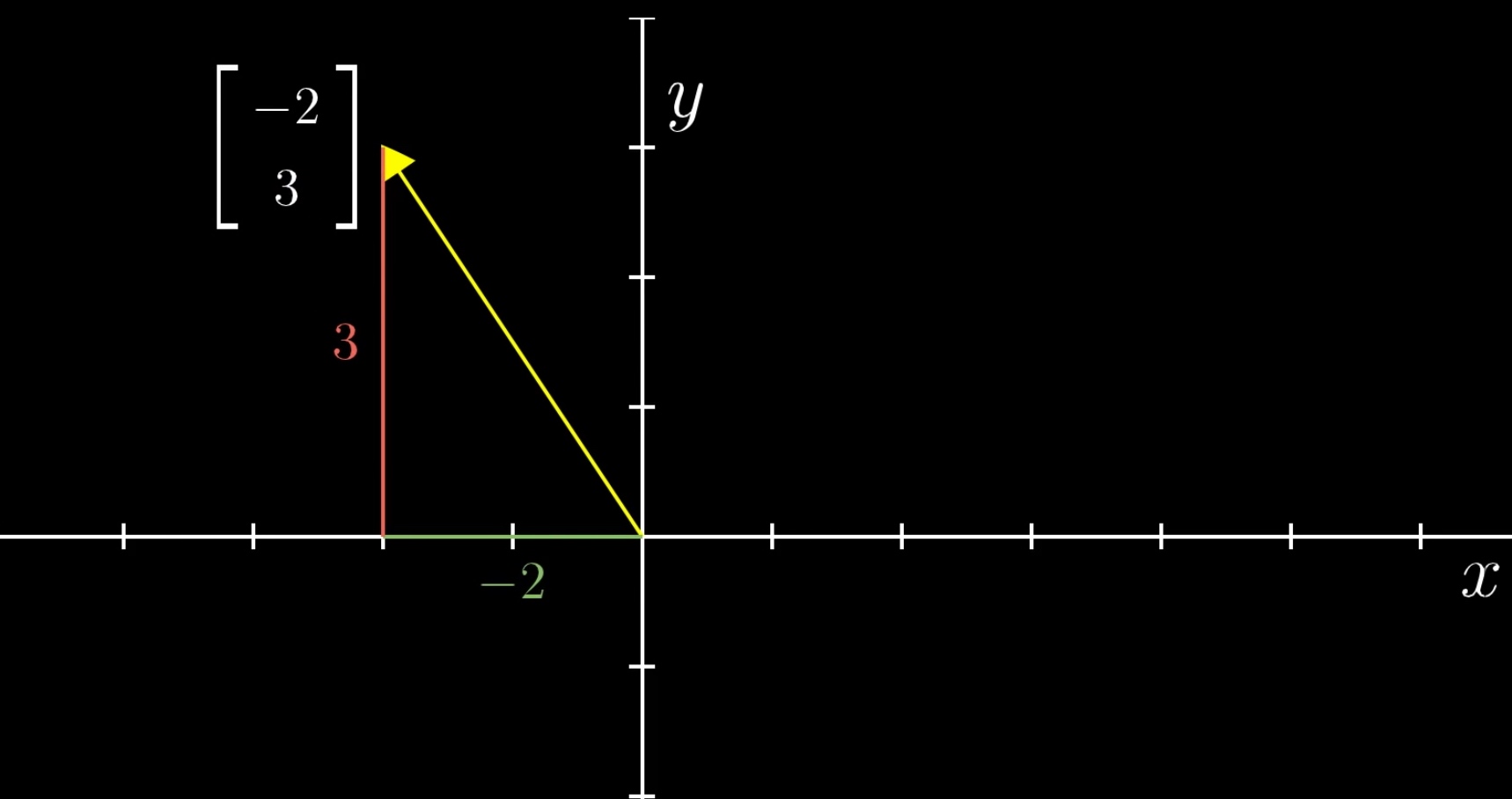

矢量，它代表一组数字，并且这些数字是有序排列的。我们用数据结构的视角来看，向量可以用**数组或者链表**来表达。

例： n 就是向量的维

区别：向量除了拥有数值的大小，还拥有方向。

• 把某个向量中的元素看作坐标轴上的坐标
• 以原点为起点，以向量代表的点为终点
• 就能形成一条有向直线。

特征向量（Feature Vector）
向量的每个元素就代表一维特征，而元素的值代表了相应特征的值。

特征向量和矩阵的特征向量（Eigenvector）是两码事。
矩阵的几何意义是坐标的变换。如果一个矩阵存在特征向量和特征值，那么这个矩阵的特征向量就表示了它在空间中最主要的运动方向。

向量的运算

向量空间

向量空间主要有特性：
（二维或者三维的坐标空间帮助理解）

• 空间由无穷多个的位置点组成；
• 这些点之间存在相对的关系；
• 可以在空间中定义任意两点之间的长度，以及任意两个向量之间的角度；
• 这个空间的点可以进行移动。

向量加法
维度相同，对应的元素相加。

向量的加法实际上就是把几何问题转化成了代数问题，然后用代数的方法实现了几何的运算。

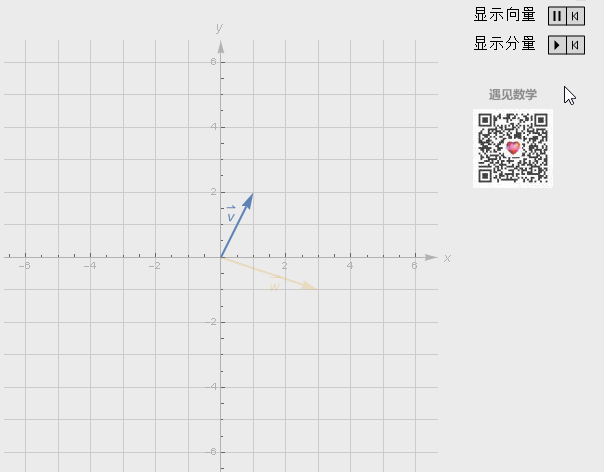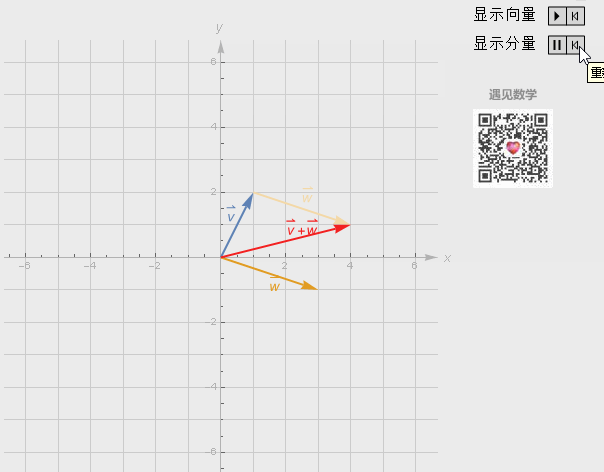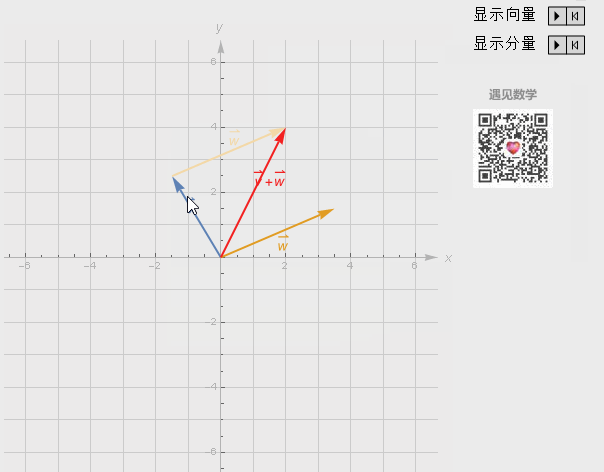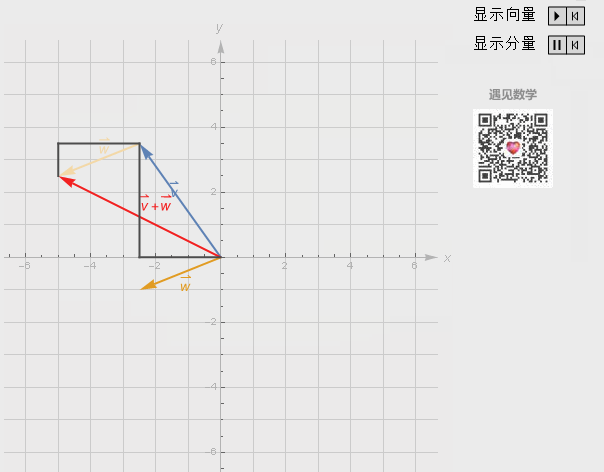
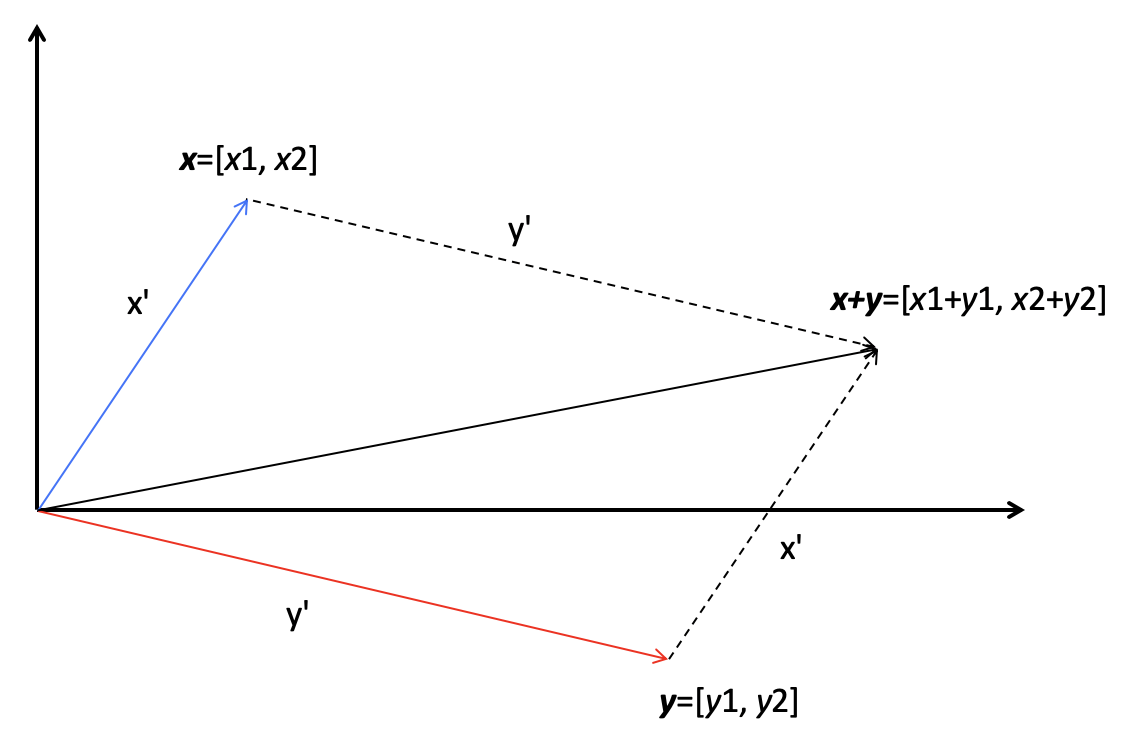
有两个向量 x 和 y，它们的长度分别是 x’和 y’，它们的相加结果是 x+y，这个结果所对应的点相当于 x 向量沿着 y 向量的方向移动 y’，或者是 y 向量沿着 x 向量的方向移动 x’。

向量同标量的乘法

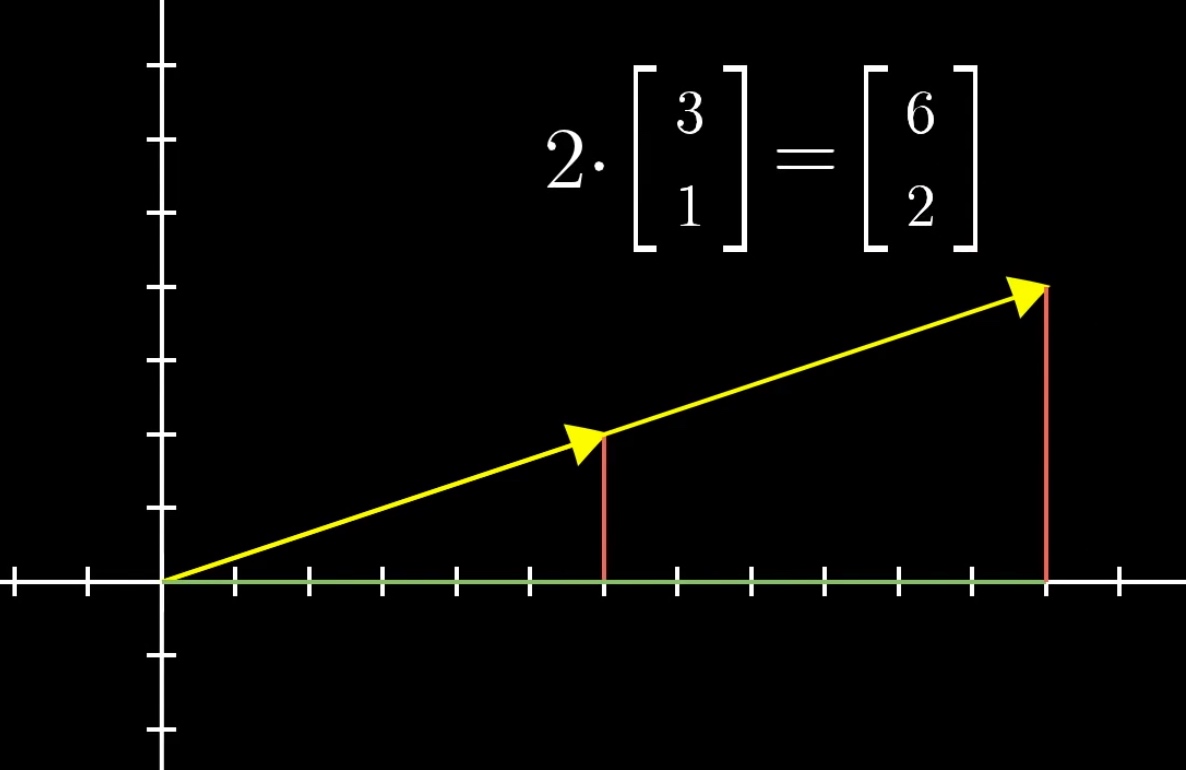
• k为标量

向量同响亮乘法

• 点乘的作用是把相乘的两个向量转换成了标量
• 点乘来计算向量的长度以及两个向量间的夹角
• 默认向量间的乘法是点乘。

矩阵的运算

矩阵由多个长度相等的向量组成，其中的每列或者每行就是一个向量。

• 数据结构角度，向量是一维数组，那矩阵就是一个二维数组

如果二维数组里绝大多数元素都是 0 或者不存在的值，那么我们就称这个矩阵很稀疏（Sparse）。对于稀疏矩阵，使用哈希表的链地址法来表示。所以，矩阵中的每个元素有两个索引。

矩阵的表示

加粗的斜体大写字母表示一个矩阵，例如，而等等，表示矩阵中的每个元素，而这里面的 n 和 m 分别表示矩阵的行维数和列维数。

向量其实也是一种特殊的矩阵。

• n × 1 的矩阵也可以称作一个 n 维列向量
• 1 × m 矩阵也称为一个 m 维行向量

同样上定义标量和矩阵之间的加法和乘法，我们只需要把标量和矩阵中的每个元素相加或相乘就可以了。矩阵加法比较简单，只要保证参与操作的两个矩阵具有相同的行维度和列维度，我们就可以把对应的元素两两相加。

矩阵的乘法

• 矩阵为矩阵和的乘积
• 是形状为 的矩阵
• 而是形状为 的矩阵
• 的列数 k 必须和的行数 k 相等，两者才可以进行这样的乘法

把这个过程看作矩阵的行向量和矩阵的列向量两两进行点乘

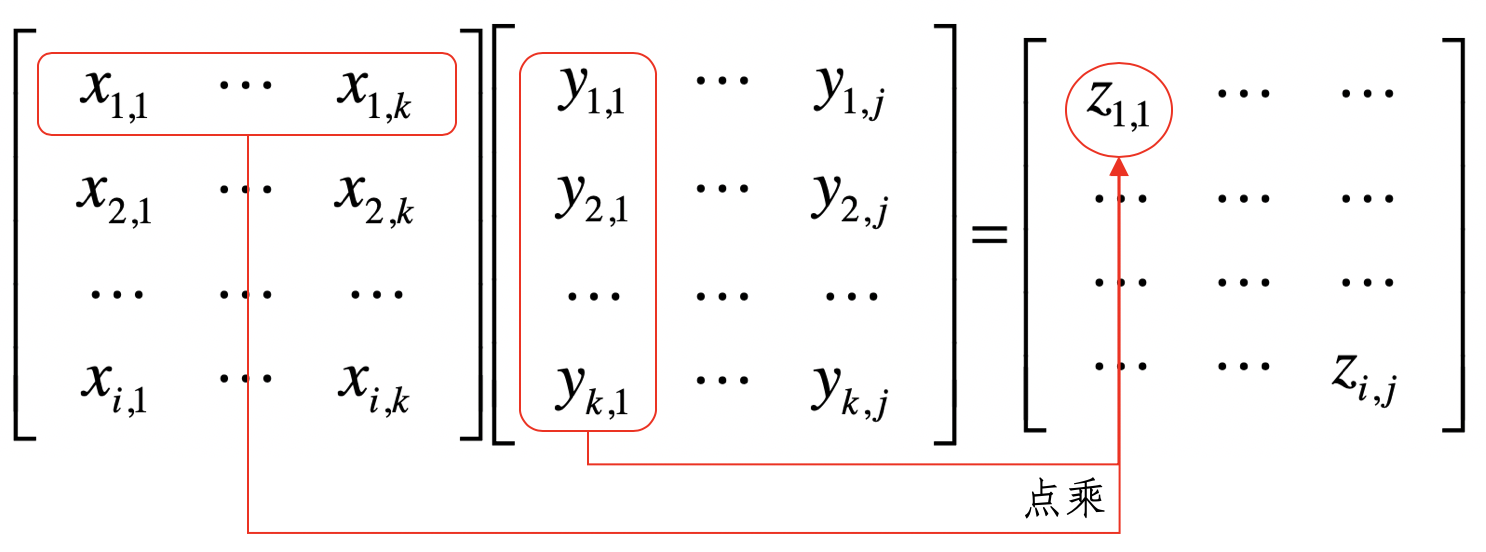
两个矩阵中对应元素进行相乘，称它为元素对应乘积，或者 Hadamard 乘积。

转置（Transposition）
是指矩阵内的元素行索引和纵索引互换，例如就变为 ，相应的，矩阵的形状由转置前的 n × m 变为转置后的 m × n。

从几何的角度来说，矩阵的转置就是原矩阵以对角线为轴进行翻转后的结果。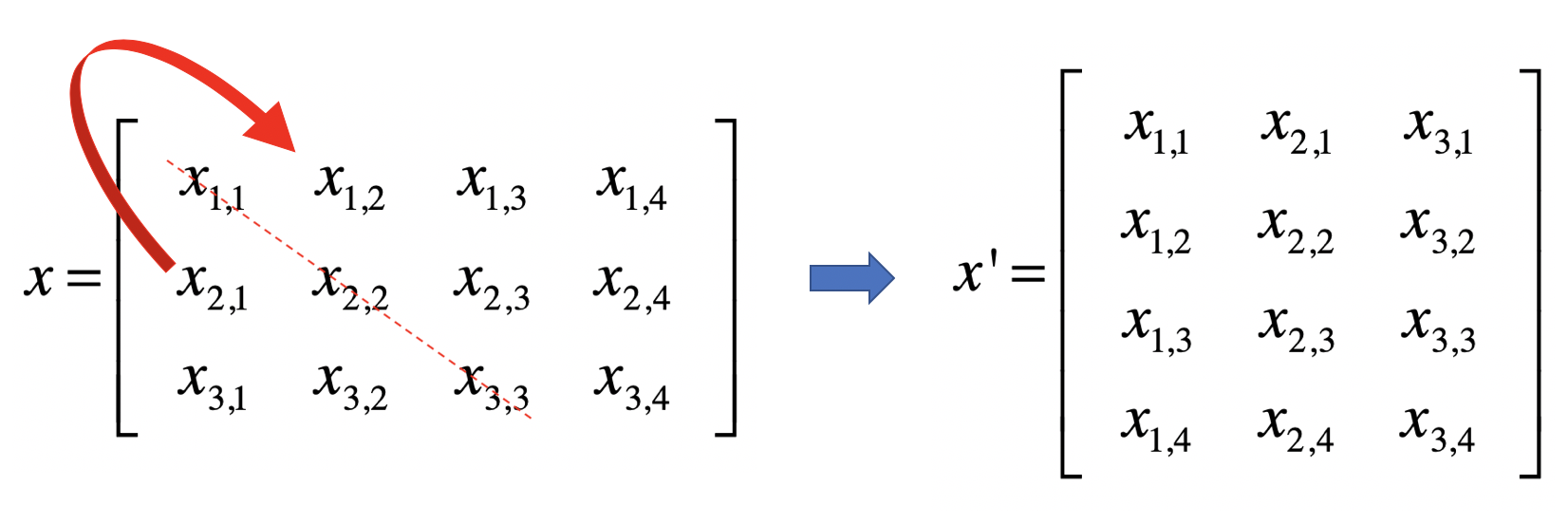

逆矩阵或矩阵逆（Matrix Inversion）

单位矩阵（Identity Matrix）

单位矩阵中，所有沿主对角线的元素都是 1，而其他位置的所有元素都是 0。通常我们只考虑单位矩阵为方阵的情况，也就是行数和列数相等，我们把它记做，表示维数。

逆矩阵

如果有矩阵，我们把它的逆矩阵记做，两者相乘的结果是单位矩阵式：X^{-1}X=I_n

特征值和奇异值的概念以及求解比较复杂了，从大体上来理解，它们可以帮助我们找到矩阵最主要的特点。通过这些操作，我们就可以在机器学习算法中降低特征向量的维度，达到特征选择和变换的目的。我会在后面的专栏，结合案例给你详细讲解。