5. 离散概率分布的运用

利用概率预测长期结果，量度预测结果的确定性。

随机变量

一个可以等于一系列数值的变量

概率分布

随机变量的概率分布，即每一个随机变量所对应的概率的集合。

• 随机变量用大写字母表示，如X或者Y
• 变量能采用的特定数值，用小写字母表示，如x或y

表示变量X取特定数值x的概率。

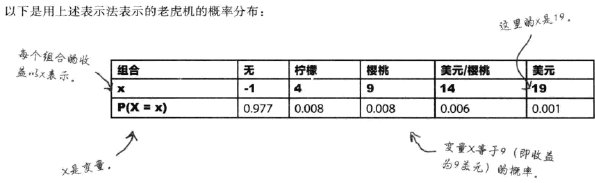
这个变量具有离散性，变量只能取确定数值。

概率分布的作用利用概率分布确定预期结果。

期望

• 类似均值，用于描述概率分布。

求解：将每个数值乘数值发生的概率，将所有乘积求和。

#card=math&code=E%EF%BC%88X%EF%BC%89%3D%5Csum%20xP%28X%3Dx%29&height=28&width=189)

方差

• 结果的分散性
  期望指出一个变量的典型值或平均值，并不提供数值分散性的任何信息。利用方差来度量这种分散性。

%3DE(X-%5Cmu)%5E2#card=math&code=Var%28X%29%3DE%28X-%5Cmu%29%5E2&height=23&width=157) 计算类比期望的计算，可以得到：

%5E2%3D%5Csum%20(x-%5Cmu)%5E2P(X%3Dx)#card=math&code=E%28X-%5Cmu%29%5E2%3D%5Csum%20%28x-%5Cmu%29%5E2P%28X%3Dx%29&height=28&width=258)

• 取每个数x，求出,所得结果乘发生概率
• 将乘积相加

#card=math&code=Var%28X%29&height=20&width=57)量度收益的变化范围。

标准差

%7D#card=math&code=%5Csigma%20%3D%20%5Csqrt%7BVar%28X%29%7D&height=35&width=105)

概率分布计算

线性变化

X（旧随机变量）与Y（新随机变量）存在线性关系，

• %3Da%20E(X)%2Bb#card=math&code=E%28Y%29%3Da%20E%28X%29%2Bb&height=20&width=138)
• %3Da%5E2Var(X)#card=math&code=Var%28Y%29%3Da%5E2Var%28X%29&height=23&width=151)

独立观测值

赌博机中，每一局称为事件，每一局的结果称为观测值，每个观测值具有相同的期望和方差

 ![](https://g.yuque.com/gr/latex?X_1#card=math&code=X_1&height=18&width=21)   第一局的观测值
![](https://g.yuque.com/gr/latex?X_2#card=math&code=X_2&height=18&width=21)   第二局的观测值
![](https://g.yuque.com/gr/latex?X_1%2CX_2#card=math&code=X_1%2CX_2&height=18&width=50)具有相同的概率分布

结果应该为：

• %3DnE(X)#card=math&code=E%28X_1%2BX_2%2BX_3%2B…%2BX_n%29%3DnE%28X%29&height=20&width=275)
• %3DnVar(X)#card=math&code=Var%28X_1%2BX_2%2BX_3%2B…%2BX_n%29%3DnVar%28X%29&height=20&width=308)

表示两个观测值，2X表示一个观测值，可能数值翻倍，二者为两个概念

随机变量加减计算

X，Y相互独立

• 加法
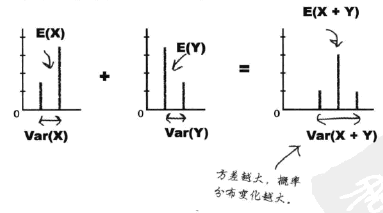
  • %2BE(Y)%3DE(X%2BY)#card=math&code=E%28X%29%2BE%28Y%29%3DE%28X%2BY%29&height=20&width=195)
  • %3DE(X)%2BE(Y)#card=math&code=E%28X%2BY%29%3DE%28X%29%2BE%28Y%29&height=20&width=195)
  • %3DVar(X)%2BVar(Y)#card=math&code=Var%28X%2BY%29%3DVar%28X%29%2BVar%28Y%29&height=20&width=245)

• 减法
  • %3DE(X)-E(Y)#card=math&code=E%28X-Y%29%3DE%28X%29-E%28Y%29&height=20&width=195)
  • %3DVar(X)%2BVar(Y)#card=math&code=Var%28X-Y%29%3DVar%28X%29%2BVar%28Y%29&height=20&width=245)

若将两个随机变量相减，方差要相加

• 线性变化相加
  • %3DaE(X)%2BbE(Y)#card=math&code=E%28aX%2BbY%29%3DaE%28X%29%2BbE%28Y%29&height=20&width=227)
  • %3Da%5E2Var(X)%2Bb%5E2Var(Y)#card=math&code=Var%28aX%2BbY%29%3Da%5E2Var%28X%29%2Bb%5E2Var%28Y%29&height=23&width=292)
• 线性变化相加
  • %3DaE(X)-bE(Y)#card=math&code=E%28aX-bY%29%3DaE%28X%29-bE%28Y%29&height=20&width=227)
  • %3Da%5E2Var(X)%2Bb%5E2Var(Y)#card=math&code=Var%28aX-bY%29%3Da%5E2Var%28X%29%2Bb%5E2Var%28Y%29&height=23&width=292)