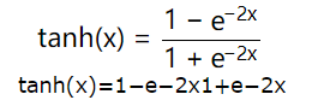(一) 神经网络基础

https://www.yuque.com/nesqi/agg42y/cpqbwp

(一) 神经网络基础

1. 神经元（Neuron）

——就像形成我们大脑基本元素的神经元一样，神经元形成神经网络的基本结构。想象一下，当我们得到新信息时我们该怎么做。当我们获取信息时，我们一般会处理它，然后生成一个输出。类似地，在神经网络的情况下，神经元接收输入，处理它并产生输出，而这个输出被发送到其他神经元用于进一步处理，或者作为最终输出进行输出。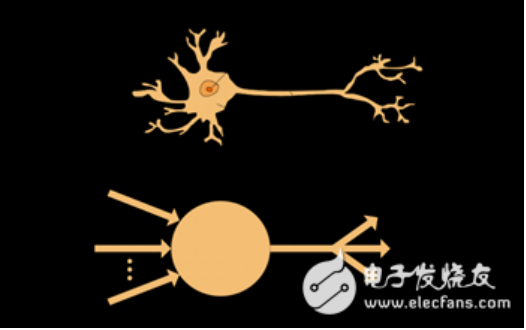

2. 权重（Weights）

——当输入进入神经元时，它会乘以一个权重。例如，如果一个神经元有两个输入，则每个输入将具有分配给它的一个关联权重。我们随机初始化权重，并在模型训练过程中更新这些权重。训练后的神经网络对其输入赋予较高的权重，这是它认为与不那么重要的输入相比更为重要的输入。为零的权重则表示特定的特征是微不足道的。
让我们假设输入为a，并且与其相关联的权重为W1，那么在通过节点之后，输入变为a * W1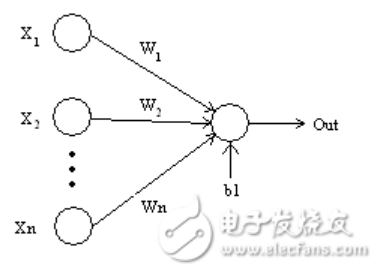

3. 偏差（Bias）

——除了权重之外，另一个被应用于输入的线性分量被称为偏差。它被加到权重与输入相乘的结果中。基本上添加偏差的目的是来改变权重与输入相乘所得结果的范围的。添加偏差后，结果将看起来像a* W1 +偏差。这是输入变换的最终线性分量。

4. 激活函数（Activation Function）

——一旦将线性分量应用于输入，将会需要应用一个非线性函数。这通过将激活函数应用于线性组合来完成。激活函数将输入信号转换为输出信号。应用激活函数后的输出看起来像f（a W1 + b），其中f（）就是激活函数。
在下图中，我们将“n”个输入给定为X1到Xn而与其相应的权重为Wk1到Wkn。我们有一个给定值为bk的偏差。权重首先乘以与其对应的输入，然后与偏差加在一起。而这个值叫做u。
U =ΣW X+ b
激活函数被应用于u，即 f(u)，并且我们会从神经元接收最终输出，如yk = f（u）。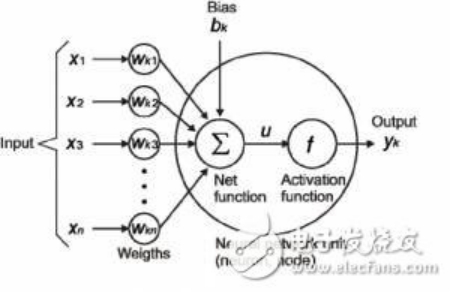

Sigmoid

——最常用的激活函数之一是Sigmoid，它被定义为：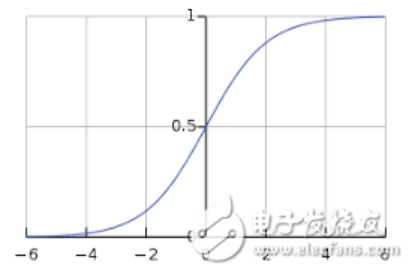

Sigmoid变换产生一个值为0到1之间更平滑的范围。我们可能需要观察在输入值略有变化时输出值中发生的变化。光滑的曲线使我们能够做到这一点，因此优于阶跃函数。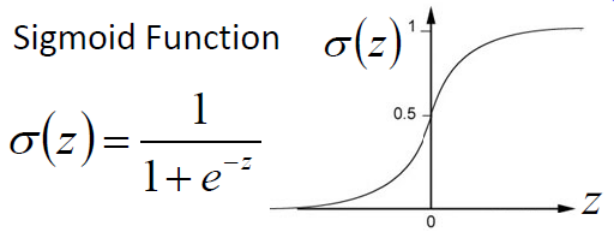

ReLU（整流线性单位）

——与Sigmoid函数不同的是，最近的网络更喜欢使用ReLu激活函数来处理隐藏层。该函数定义为：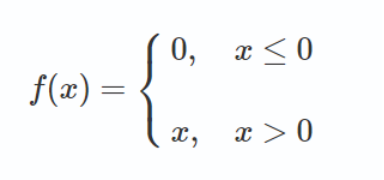

当X>0时，函数的输出值为X；当X<=0时，输出值为0。函数图如下图所示：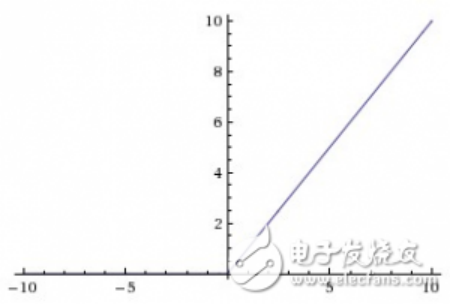

使用ReLU函数的最主要的好处是对于大于0的所有输入来说，它都有一个不变的导数值。常数导数值有助于网络训练进行得更快。

Softmax

——Softmax激活函数通常用于输出层，用于分类问题。它与sigmoid函数是很类似的，唯一的区别就是输出被归一化为总和为1。Sigmoid函数将发挥作用以防我们有一个二进制输出，但是如果我们有一个多类分类问题，softmax函数使为每个类分配值这种操作变得相当简单，而这可以将其解释为概率。
以这种方式来操作的话，我们很容易看到——假设你正在尝试识别一个可能看起来像8的6。该函数将为每个数字分配值如下。我们可以很容易地看出，最高概率被分配给6，而下一个最高概率分配给8，依此类推……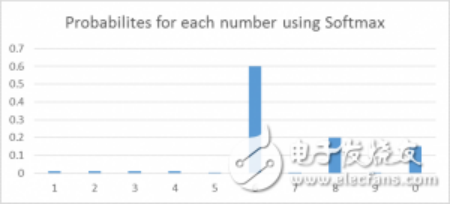


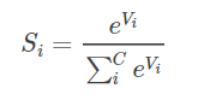
其中，Vi 是分类器前级输出单元的输出。i 表示类别索引，总的类别个数为 C。Si 表示的是当前元素的指数与所有元素指数和的比值。Softmax 将多分类的输出数值转化为相对概率，更容易理解和比较。
因为有指数运算，如果V值数值很大，可能有溢出的风险，所以需要对V进行一些处理：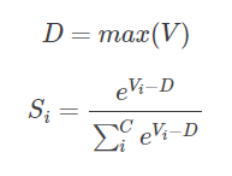

Tanh

几个激活函数的对比：

https://blog.csdn.net/qq_34638161/article/details/81902989
https://www.cnblogs.com/makefile/p/activation-function.html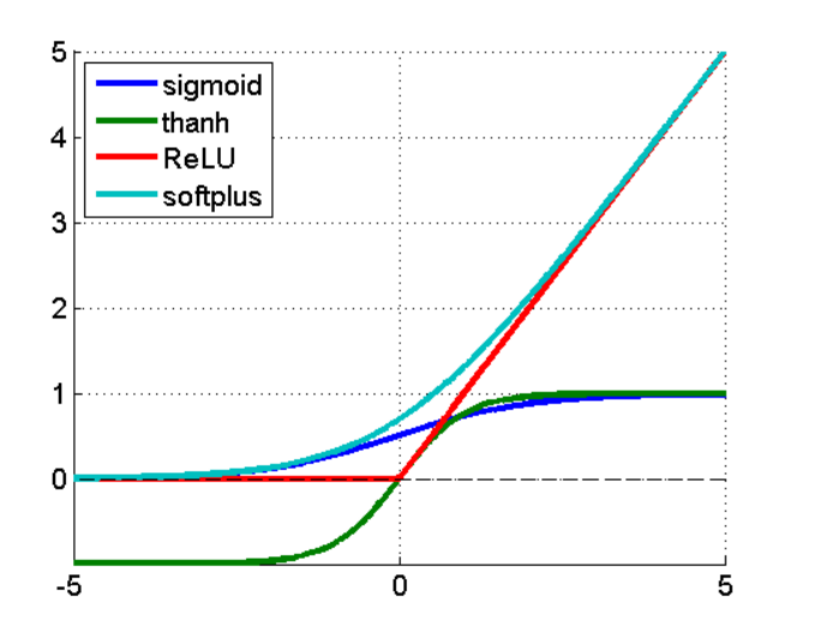

5. 局部感受野，感受野

用猫做实验，当物体在猫的上方时，神经A区有反应，物体在猫的下方时，神经B区有反应…
在卷积神经网络中，感受野的定义是 卷积神经网络每一层输出的特征图（feature map）上的像素点在原始图像上映射的区域大小

6. 神经网络（Neural Network）

——神经网络构成了深度学习的支柱。神经网络的目标是找到一个未知函数的近似值。它由相互联系的神经元形成。这些神经元具有权重和在网络训练期间根据错误来进行更新的偏差。激活函数将非线性变换置于线性组合，而这个线性组合稍后会生成输出。激活的神经元的组合会给出输出值。
一个很好的神经网络定义——
“神经网络由许多相互关联的概念化的人造神经元组成，它们之间传递相互数据，并且具有根据网络”经验“调整的相关权重。神经元具有激活阈值，如果通过其相关权重的组合和传递给他们的数据满足这个阈值的话，其将被解雇;发射神经元的组合导致“学习”。

7. 输入/输出/隐藏层（Input / Output / Hidden Layer）

——正如它们名字所代表的那样，输入层是接收输入那一层，本质上是网络的第一层。而输出层是生成输出的那一层，也可以说是网络的最终层。处理层是网络中的隐藏层。这些隐藏层是对传入数据执行特定任务并将其生成的输出传递到下一层的那些层。输入和输出层是我们可见的，而中间层则是隐藏的。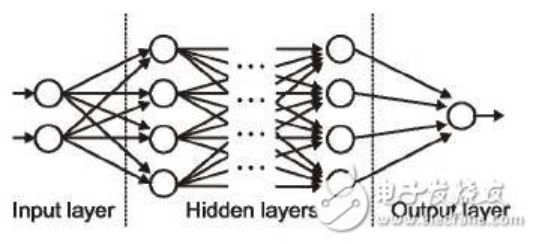

8. MLP（多层感知器）

——单个神经元将无法执行高度复杂的任务。因此，我们使用堆栈的神经元来生成我们所需要的输出。在最简单的网络中，我们将有一个输入层、一个隐藏层和一个输出层。每个层都有多个神经元，并且每个层中的所有神经元都连接到下一层的所有神经元。这些网络也可以被称为完全连接的网络。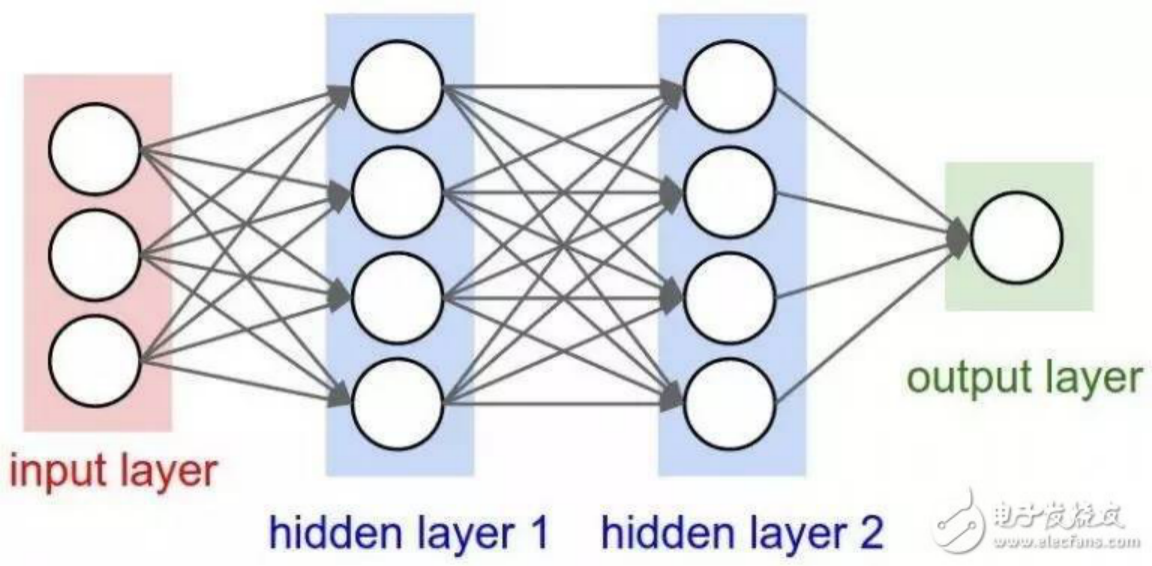

9. 正向传播（Forward Propagation）

——正向传播是指输入通过隐藏层到输出层的运动。在正向传播中，信息沿着一个单一方向前进。输入层将输入提供给隐藏层，然后生成输出。这过程中是没有反向运动的。

10. 成本函数（Cost Function）

——当我们建立一个网络时，网络试图将输出预测得尽可能靠近实际值。我们使用成本/损失函数来衡量网络的准确性。而成本或损失函数会在发生错误时尝试惩罚网络。
我们在运行网络时的目标是提高我们的预测精度并减少误差，从而最大限度地降低成本。最优化的输出是那些成本或损失函数值最小的输出。
如果我将成本函数定义为均方误差，则可以写为：
C= 1/m ∑(y–a)^2，
其中m是训练输入的数量，a是预测值，y是该特定示例的实际值。
学习过程围绕最小化成本来进行。

11. 梯度下降（Gradient Descent）

——梯度下降是一种最小化成本的优化算法。要直观地想一想，在爬山的时候，你应该会采取小步骤，一步一步走下来，而不是一下子跳下来。因此，我们所做的就是，如果我们从一个点x开始，我们向下移动一点，即Δh，并将我们的位置更新为x-Δh，并且我们继续保持一致，直到达到底部。考虑最低成本点。

在数学上，为了找到函数的局部最小值，我们通常采取与函数梯度的负数成比例的步长。
你可以通过这篇文章来详细了解梯度下降。

12. 学习率（Learning Rate）

——学习率被定义为每次迭代中成本函数中最小化的量。简单来说，我们下降到成本函数的最小值的速率是学习率。我们应该非常仔细地选择学习率，因为它不应该是非常大的，以至于最佳解决方案被错过，也不应该非常低，以至于网络需要融合。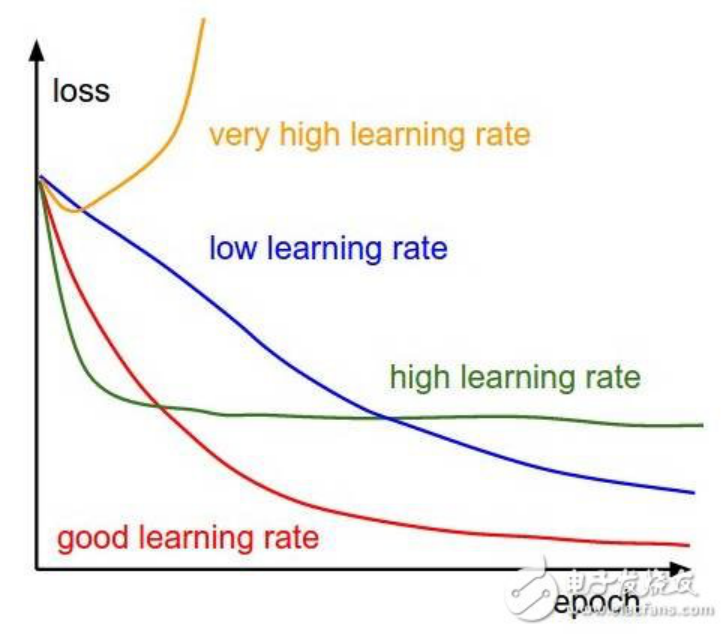

13. 反向传播（Backpropagation）

——当我们定义神经网络时，我们为我们的节点分配随机权重和偏差值。一旦我们收到单次迭代的输出，我们就可以计算出网络的错误。然后将该错误与成本函数的梯度一起反馈给网络以更新网络的权重。 最后更新这些权重，以便减少后续迭代中的错误。使用成本函数的梯度的权重的更新被称为反向传播。
在反向传播中，网络的运动是向后的，错误随着梯度从外层通过隐藏层流回，权重被更新。

14. 批次（Batches）

——在训练神经网络的同时，不用一次发送整个输入，我们将输入分成几个随机大小相等的块。与整个数据集一次性馈送到网络时建立的模型相比，批量训练数据使得模型更加广义化。

15. 周期（Epochs）

——周期被定义为向前和向后传播中所有批次的单次训练迭代。这意味着1个周期是整个输入数据的单次向前和向后传递。
你可以选择你用来训练网络的周期数量，更多的周期将显示出更高的网络准确性，然而，网络融合也需要更长的时间。另外，你必须注意，如果周期数太高，网络可能会过度拟合。

16. 丢弃（Dropout）

——Dropout是一种正则化技术，可防止网络过度拟合套。顾名思义，在训练期间，隐藏层中的一定数量的神经元被随机地丢弃。这意味着训练发生在神经网络的不同组合的神经网络的几个架构上。你可以将Dropout视为一种综合技术，然后将多个网络的输出用于产生最终输出。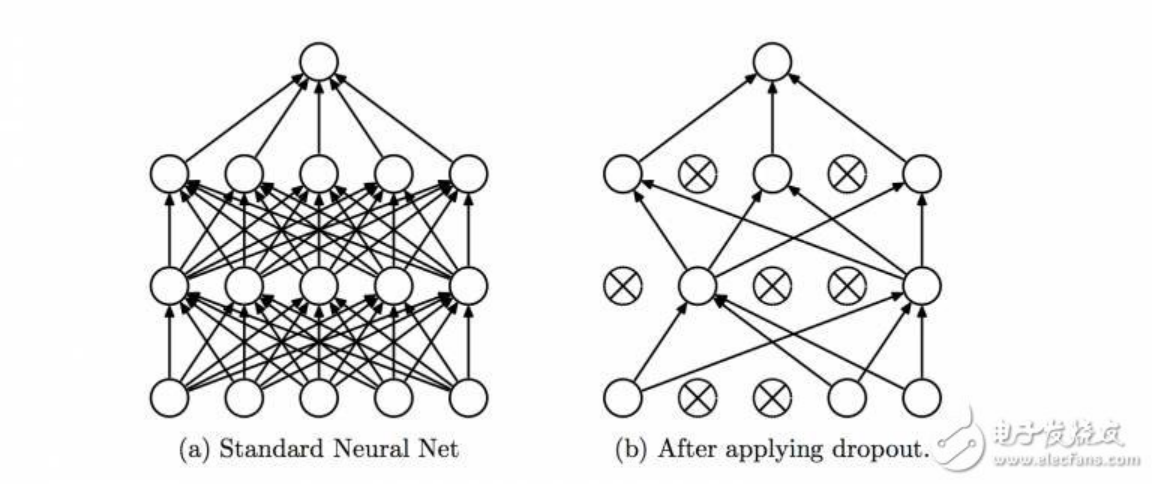

17. 批量归一化（Batch Normalization）

——作为一个概念，批量归一化可以被认为是我们在河流中设定为特定检查点的水坝。这样做是为了确保数据的分发与希望获得的下一层相同。当我们训练神经网络时，权重在梯度下降的每个步骤之后都会改变，这会改变数据的形状如何发送到下一层。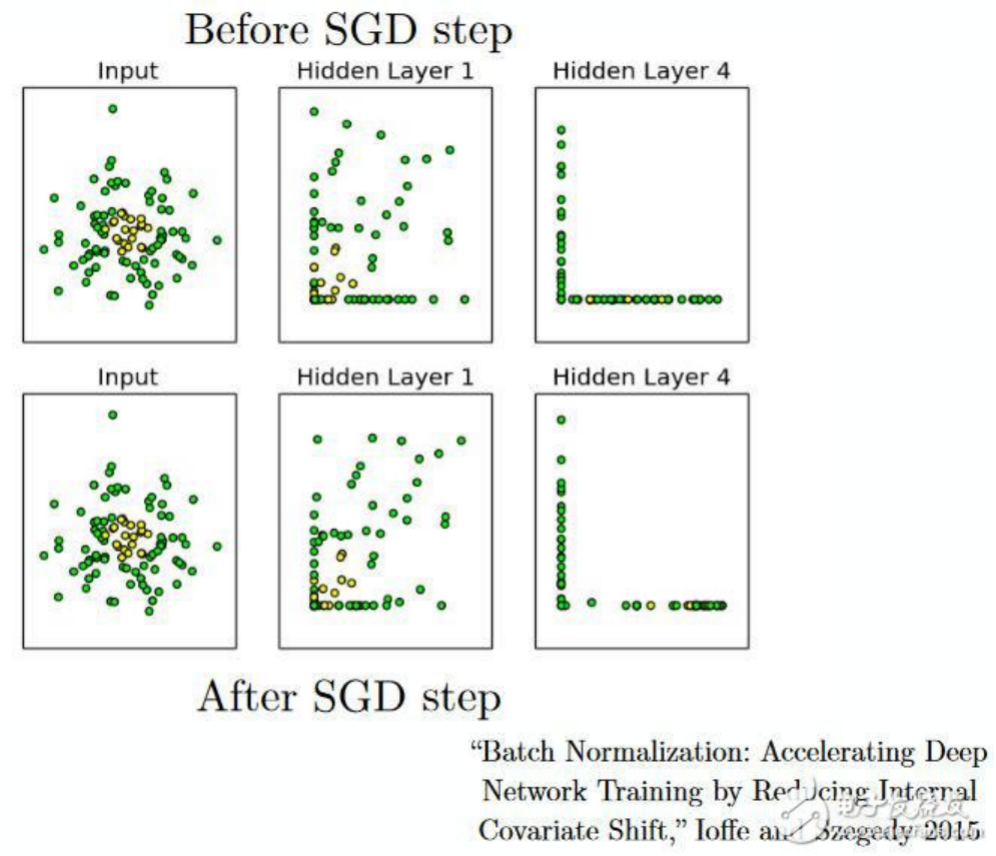

但是下一层预期分布类似于之前所看到的分布。 所以我们在将数据发送到下一层之前明确规范化数据。

参考：https://blog.csdn.net/solomon1558/article/details/44689611

18. 过拟合

概念：
为了得到一致假设而使假设变得过度严格。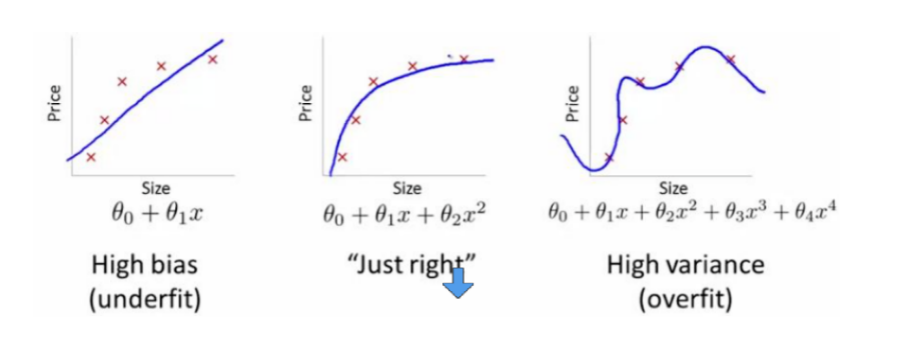

出现的原因：
l 训练集的数量级和模型的复杂度不匹配。训练集的数量级要小于模型的复杂度。
l 训练集和测试集特征分布不一致。
l 样本里的噪音数据干扰过大，大到模型过分记住了噪音特征，从而忽略了输入输出间的关系。
l 权值学习迭代次数足够多，拟合了训练数据中的噪声和训练样例中没有代表性的特征。

解决方案
Ø 1，simpler model structure 调小模型复杂度，使适合自己的训练集的数量级。
Ø 2，data augmentation 数据参数，训练集越多，过拟合的概率越小，所以增广的方式是对图像进行旋转，缩放，剪切等 。
Ø 3，regularization ，正则化
Ø 4，dropout 丢弃，训练过程中丢弃部分的神经元
Ø 5，early stopping 在每个周期的训练中，当有效值的精度不再提高时，就停止训练。
Ø 6，ensemble 集成学习算法减轻过拟合