leetcode 091.解码方法（动态规划、递推）

方法一：动态规划思路与算法

对于给定的字符串 s，设它的长度为 n，其中的字符从左到右依次为s[1],s[2],⋯,s[n]。我们可以使用动态规划的方法计算出字符串 s 的解码方法数。

具体地，设f[i]表示字符串 s 的前i 个字符 s[1..i] 的解码方法数。在进行状态转移时，我们可以考虑最后一次解码使用了 s 中的哪些字符，那么会有下面的两种情况：

• 第一种情况是我们使用了一个字符，即 s[i] 进行解码，那么只要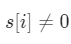，它就可以被解码成A∼I 中的某个字母。由于剩余的前i−1 个字符的解码方法数为f i−1，因此我们可以写出状态转移方程：

• 第二种情况是我们使用了两个字符，即 s[i−1] 和 s[i] 进行编码。与第一种情况类似，s[i−1] 不能等于0，并且 s[i−1] 和 s[i] 组成的整数必须小于等于 26，这样它们就可以被解码成J∼Z 中的某个字母。由于剩余的前 i-2i−2 个字符的解码方法数为f i−2 ,因此我们可以写出状态转移方程：

需要注意的是，只有当 i>1i>1 时才能进行转移，否则 s[i-1]s[i−1] 不存在。

将上面的两种状态转移方程在对应的条件满足时进行累加，即可得到f i的值。在动态规划完成后，最终的答案即为 f n

细节

动态规划的边界条件为：

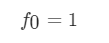
即空字符串可以有11种解码方法，解码出一个空字符串。

同时，由于在大部分语言中，字符串的下标是从0 而不是 1 开始的，因此在代码的编写过程中，我们需要将所有字符串的下标减去 1，与使用的语言保持一致。

代码

class Solution {
    public int numDecodings(String s) {
        int n = s.length();
        int[] f = new int[n + 1];
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            if (s.charAt(i - 1) != '0') {
                f[i] += f[i - 1];
            }
            if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {
                f[i] += f[i - 2];
            }
        }
        return f[n];
    }
}

注意到在状态转移方程中，f i的值仅与 f i−1和 f i−2有关，因此我们可以使用三个变量进行状态转移，省去数组的空间。

class Solution {
    public int numDecodings(String s) {
        int n = s.length();
        // a = f[i-2], b = f[i-1], c=f[i]
        int a = 0, b = 1, c = 0;
        for (int i = 1; i <= n; ++i) {
            c = 0;
            if (s.charAt(i - 1) != '0') {
                c += b;
            }
            if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {
                c += a;
            }
            a = b;
            b = c;
        }
        return c;
    }
}

复杂度分析

• 时间复杂度：O(n)，其中 n 是字符串s 的长度。
• 空间复杂度：O(n) 或O(1)。如果使用数组进行状态转移，空间复杂度为O(n)；如果仅使用三个变量，空间复杂度为O(1)。