思路与算法

由于输入的两个链表都是逆序存储数字的位数的，因此两个链表中同一位置的数字可以直接相加。

我们同时遍历两个链表，逐位计算它们的和，并与当前位置的进位值相加。具体而言，如果当前两个链表处相应位置的数字为 n1,n2n1,n2，进位值为}carry，则它们的和为 n1+n2+carry；其中，答案链表处相应位置的数字为 (n1+n2+carry)mod10，而新的进位值为 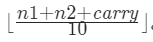image.png

如果两个链表的长度不同，则可以认为长度短的链表的后面有若干个 00 。

此外，如果链表遍历结束后，有 carry>0，还需要在答案链表的后面附加一个节点，节点的值为 carry。

  • 小技巧：对于链表问题，返回结果为头结点时，通常需要先初始化一个预先指针 pre，该指针的下一个节点指向真正的头结点head。使用预先指针的目的在于链表初始化时无可用节点值，而且链表构造过程需要指针移动，进而会导致头指针丢失，无法返回结果。

    代码

    1. class Solution {
    2.   public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    3.       ListNode head = null, tail = null;
    4.       int carry = 0;
    5.       while (l1 != null || l2 != null) {
    6.           int n1 = l1 != null ? l1.val : 0;
    7.           int n2 = l2 != null ? l2.val : 0;
    8.           int sum = n1 + n2 + carry;
    9.           if (head == null) {
    10.               head = tail = new ListNode(sum % 10);
    11.           } else {
    12.               tail.next = new ListNode(sum % 10);
    13.               tail = tail.next;
    14.           }
    15.           carry = sum / 10;
    16.           if (l1 != null) {
    17.               l1 = l1.next;
    18.           }
    19.           if (l2 != null) {
    20.               l2 = l2.next;
    21.           }
    22.       }
    23.       if (carry > 0) {
    24.           tail.next = new ListNode(carry);
    25.       }
    26.       return head;
    27.   }
    28. }

    复杂度分析

  • 时间复杂度：O(max(m,n))，其中 m 和 n 分别为两个链表的长度。我们要遍历两个链表的全部位置，而处理每个位置只需要O(1) 的时间。

  • 空间复杂度：O(1)。注意返回值不计入空间复杂度。