混淆矩阵
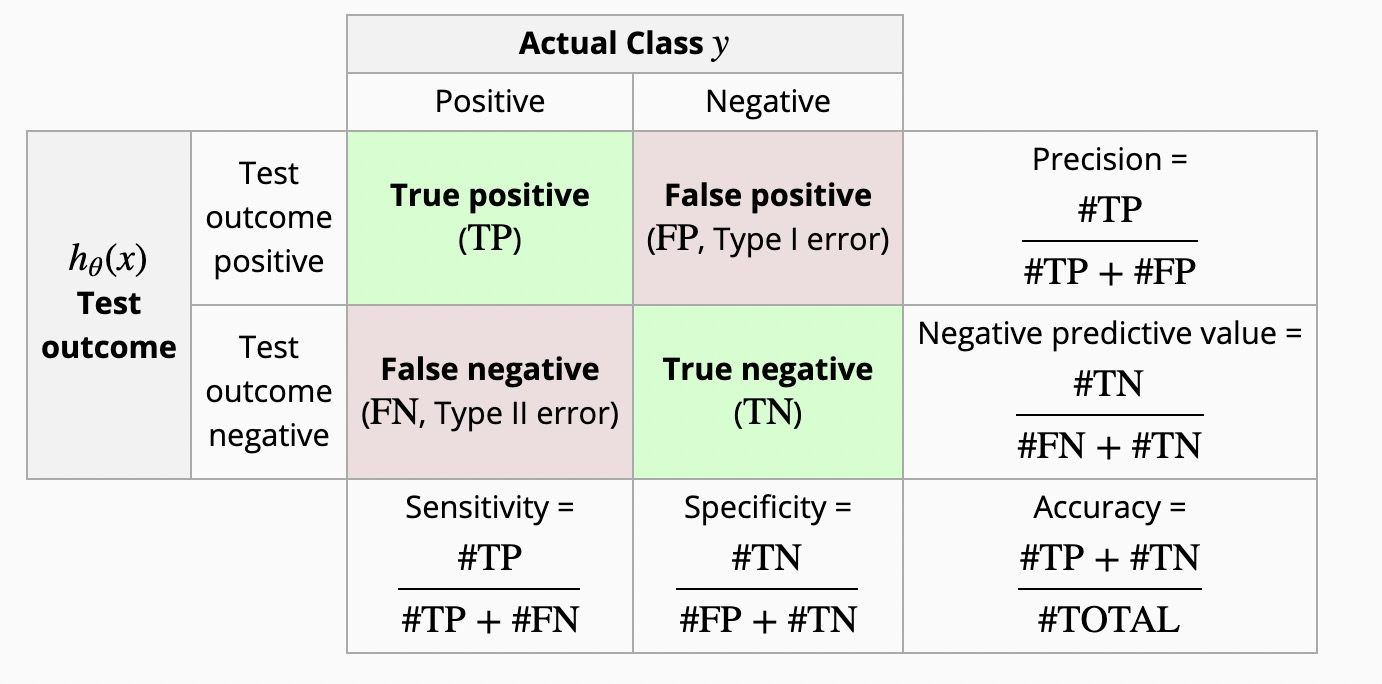
TP/FP/TN/FN可以这么理解,如FP,P/N表示预测的结果,T/F表示是否预测对了。
FPR表示给一个负样本,预测错误的概率,这当然是越小越好。
TPR表示给一个正样本,预测正确的概率,这是越大越好。
Precision - 精确率,从字面理解,精确表示预测为正的样本中,有多少是真正的正样本。
Recall - 召回率,从字面理解,召回表示样本中的正例有多少被预测正确了。
F1-Score - 精确率和召回率的调和均值,通常用于不平衡二分类问题中来衡量模型效果。
macro/micro
如果是多分类问题,就可能存在多个混淆矩阵,例如我们可以把每个类别当做正样本,其他类别当做负样本;或者每两个类别都进行组合,产生一个混淆矩阵;或者我们同一个数据集进行了多次试验;或者我们在多个数据集上进行了试验;我们希望得到一个全局的指标。那么此时就应用macro或micro进行综合。以多分类为例:
- macro - 对每个类别分别计算其P和R,然后计算所有类别的平均P和R。
对于多分类,可以理解为计算每个类别的P和R时,都是把该分类当做正样本,其他分类当做负样本,先计算每个分类的P和R,然后求平均值。注意在sklearn中是直接求每个类的平均F1,不是按照上面公式求的。
- micro
micro是先对每个分类计算TP,FP,FN,然后求平均值,再计算P和R。注意在sklearn中是把所有类别当做一类,所以micro-P=micro-R=accuracy。
参考:来自周志华《机器学习》chapter 2.3
sklearn 实例
下面以sklearn中的实例来看一下计算过程:
y_true = [0, 1, 2, 0, 1, 2] # 实际labely_pred = [0, 2, 1, 0, 0, 1] # 预测label
| TP | FP | FN | precision | recall | f1 | |
|---|---|---|---|---|---|---|
| 0 | 2 | 1 | 0 | 0.667 | 1 | 0.8 |
| 1 | 0 | 2 | 2 | 0 | 0 | 0 |
| 2 | 0 | 1 | 2 | 0 | 0 | 0 |
| macro-p | =(p0+p1+p2)/3=(0.667+0+0)/3=0.22 | |||||
| macro-r | =(r0+r1+r2)/3=(1+0+0)/3=0.33 | |||||
| macro-f1 | =(macro-f1_0+macro-f1_1+macro-f1_2)/3=0.26 | |||||
| micro-p | tp=(tp0+tp1+tp2)/3=(2+0+0)/3=0.66 fp=(fp0+fp1+fp2)/3=(1+2+1)/3=1.33 micro-p= (20.661.33)/(0.66+1.33)=0.88 (按照上面的micro的计算方法得到的结果,与sklearn不一致) |
- precision
来看一下具体的计算过程:对标签0来说,TP表示预测为0的实际有多少为0,那么预测有3个为0,实际有2个;FP表示预测为0,实际不为0,有1个;FN表示预测不为0,但实际为0,没有。标签1和标签2同理。
所以对标签0,precision=TP/(TP+FP)=2/3=0.667
对sklearn来说,还提供了macro-precision、micro-precision、weighted-precision
macro-p是计算每个标签的precision,然后计算平均值=(0.667+0+0)/3=0.22
micro-p是将所有样本看做一个标签,然后计算precision,例如TP表示预测正确的=2,FP表示预测错误的=4,micro-p=2/6=0.33。所以对于micro来说,就是样本预测的对错,实际就是正确率和错误率,所以micro-p=micro-r=micro-f1。注意,sklearn的micro的定义与上面写的不太一样,他是把所有标签当做一个类别,只有正确和错误。
weighted-p是将每个标签的数量占比作为权重,这里都是1/3,所以weighted-p=1/3P0+1/3P1+1/3*P2=0.22。
- recall与precision的计算方法一致。
- f1
注意,sklearn的macro-f1也与上面的公式不一样。sklearn的macro-f1是在各个类别f1上直接平均来的,而不是用macro-p和macro-r计算得到的。
所以,即使对于二分类,macro-f1和micro-f1与我们通常讲的f1也是不一样的,因为我们通常说的f1是指label=1的f1,而macro-f1和micro-f1还考虑了label=0时的f1。对于二分类,通常我们只关注label=1的p、r、f1,而对于多分类,我们才会考虑使用macro、micro、weighted等。
y_true = [0, 1, 1, 0, 1, 1]y_pred = [0, 0, 1, 0, 0, 1]print(precision_score(y_true, y_pred, average='macro')) # 分类别,然后算平均值print(precision_score(y_true, y_pred, average='micro')) # 相当于正确率print(precision_score(y_true, y_pred, average=None)) # 分类别算print(precision_score(y_true, y_pred)) # 算label=1的---0.750.6666666666666666[0.5 1. ]1.0
ROC、AUC
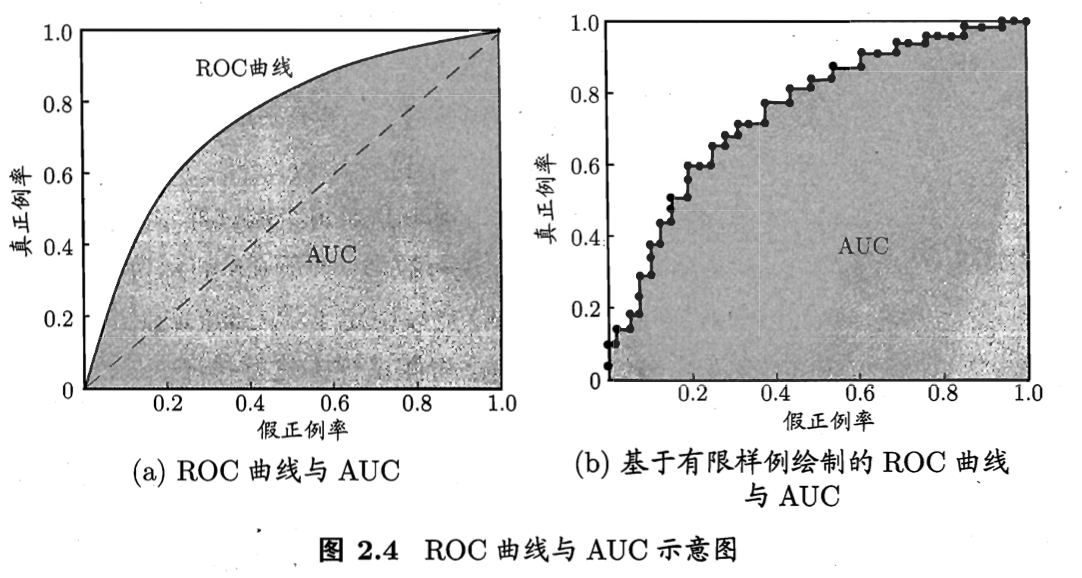
首先来看这张图,横轴是假正例率,也就是FPR,就是在预测为正的样本中,预测错的比例;纵轴是真正例率,也就是预测为正的样本中,预测对的比例。虚线表示随机猜测,也就是预测为正的样本中,预测对和预测错的比例相等。
AUC为什么能反映排序质量的好坏?
Mann–Whitney U test(曼-惠特尼U检验)与AUC的计算一致,而Mann–Whitney U test的物理意义就是测试任意给一个正类样本和一个负类样本,正类样本的score有多大的概率大于负类样本的score。所以,AUC的物理意义也可以从排序质量去理解。至于为什么Mann–Whitney U test的物理意义是这个,可以从统计学的书去了解,这里暂时不讲了。
假设一个数据集有15个样本,实际的label和预测的得分如下:
| rank | i in e | label | score(100%) |
|---|---|---|---|
| 1 | 1 | 1 | 98.4 |
| 2 | 2 | 1 | 95.2 |
| 3 | 3 | 1 | 94.4 |
| 4 | 0 | 92.8 | |
| 5 | 4 | 1 | 83.2 |
| 6 | 5 | 1 | 81.6 |
| 7 | 6 | 1 | 58.4 |
| 8 | 0 | 57.6 | |
| 9 | 0 | 28.0 | |
| 10 | 0 | 13.6 | |
| 11 | 7 | 1 | 3.2 |
| 12 | 0 | 2.4 | |
| 13 | 0 | 1.6 | |
| 14 | 0 | 0.8 | |
| 15 | 0 | 0 |

举例来说,当时,就有1个负例,当
,此时也就只有1个负例,当
,说明此时有4个负例,按照此方法,计算得到F=7,分别是:
| i in e | F |
|---|---|
| i=4 | 1 |
| i=5 | 1 |
| i=6 | 1 |
| i=7 | 4 |
| sum | 7 |
引用
- https://blog.csdn.net/AckClinkz/article/details/89397481
- 10.1.1.458.8392.pdf
TOP K
推荐系统中,常常我们只对用户展示top k个预测结果,所以,我们的指标需要看的就是在top k个预测结果里,我们的准确率,精确率,召回率,F1等等指标。
在从预测中按得分降序取top k 个,然后从实际的数据中按得分降序取top k个,两者取交集
precesion at top k = 交集个数 / 预测的k,表示在预测的k个中,有多少预测对了
recall at top k = 交集个数 / 实际的k,表示在实际的k个中,有多少被预测出来了
Q:如果是二分类,实际样本只有0-1,如果排序得到top k?
另外一个就是,precision和recall其实是对所有用户的一个结果,如果是排序top k,还跟用户有关吗?这里还引出了一个问题,在推荐是针对具体用户而言的,你是如何去确定precesion和recall的呢?
猜测:是不是对每个用户,都计算一个指标?整体指标,只是用户指标的一个平均而已
排序-NDCG
大意是标准化之后的排序质量,也就是分子为每个用户对当前Item的评分*该Item的排名折扣(排名越低,折扣越多),然后对所有Item求和。再除以按照完美的排序得到的求和结果,完美排序也就是Item按照评分降序排列。
http://sofasofa.io/forum_main_post.php?postid=1002561
引用:

