伪代码图
实例讲解
如下表所示:一组数据,特征为年龄、体重,身高为标签值。共有5条数据,前四条为训练样本,最后一条为要预测的样本。
| 编号 | 年龄(岁) | 体重(kg) | 身高(m)(标签值) |
|---|---|---|---|
| 1 | 5 | 20 | 1.1 |
| 2 | 7 | 30 | 1.3 |
| 3 | 21 | 70 | 1.7 |
| 4 | 30 | 60 | 1.8 |
| 5 | 25 | 65 | ? |
1. 初始化弱学习器:
%3Dargmin%7B%5Cgamma%7D%20%5Cdisplaystyle%5Csum%7Bi%3D1%7D%5E%7BN%7D%20L(yi%2C%5Cgamma)%0A#card=math&code=f_0%28x%29%3Dargmin%7B%5Cgamma%7D%20%5Cdisplaystyle%5Csum_%7Bi%3D1%7D%5E%7BN%7D%20L%28y_i%2C%5Cgamma%29%0A&height=53&width=209)
由于此时只有根节点,样本1,2,3,4都在根节点,此时要找到使得平方损失函数最小的参数 ,怎么求呢?平方损失显然是一个凸函数,直接求导,导数等于零,得到
。
%7D%7B%5Cpartial%20%5Cgamma%7D%20%3D%20%5Cfrac%7B%5Cpartial(%5Cfrac%7B1%7D%7B2%7D(y-%5Cgamma)%5E2)%7D%7B%5Cpartial%20%5Cgamma%7D%3D%5Cgamma-y%3D0%20%0A#card=math&code=%5Cfrac%7B%5Cpartial%20L%28y_i%2C%20%5Cgamma%29%7D%7B%5Cpartial%20%5Cgamma%7D%20%3D%20%5Cfrac%7B%5Cpartial%28%5Cfrac%7B1%7D%7B2%7D%28y-%5Cgamma%29%5E2%29%7D%7B%5Cpartial%20%5Cgamma%7D%3D%5Cgamma-y%3D0%20%0A&height=50&width=284)
求得, 。
所以,考虑到有N个样本,,初始化时,
为所有训练样本标签值的均值,即
%2F4%3D1.475#card=math&code=%5Cgamma%3D%281.1%2B1.3%2B1.7%2B1.8%29%2F4%3D1.475&height=20&width=270),此时,得到初始化学习器
#card=math&code=f_0%28x%29&height=20&width=38):
%3D%5Cgamma%3D1.475%0A#card=math&code=f_0%28x%29%3D%5Cgamma%3D1.475%0A&height=20&width=131)
2. 对迭代轮数m=1:
计算负梯度
)%7D%7B%5Cpartial%20f(xi)%7D%20%5Cbigg%5D%7Bf(x)%3Df0(x)%7D%3Df(x_i)-y_i%0A#card=math&code=%5Cgamma%7Bi1%7D%3D-%5Cbigg%5B%20%5Cfrac%7B%5Cpartial%20L%28yi%2Cf%28x_i%29%29%7D%7B%5Cpartial%20f%28x_i%29%7D%20%5Cbigg%5D%7Bf%28x%29%3Df_0%28x%29%7D%3Df%28x_i%29-y_i%0A&height=49&width=329)
如上面 1. 初始化弱学习器 所讲,如果我们采用平方损失函数,那么,这里的结果,其实就是残差(残差指实际观察值与估计值之间的差),如下表列出。
| 编号 | 真实值 | 残差 | |
|---|---|---|---|
| 1 | 1.1 | 1.475 | -0.375 |
| 2 | 1.3 | 1.475 | -0.175 |
| 3 | 1.7 | 1.475 | 0.225 |
| 4 | 1.8 | 1.475 | 0.325 |
此时,将残差作为样本的真实值训练#card=math&code=f_1%28x%29&height=20&width=38),即下表数据
| 编号 | 年龄(岁) | 体重(kg) | 身高(m)(标签值) |
|---|---|---|---|
| 1 | 5 | 20 | -0.375 |
| 2 | 7 | 30 | -0.175 |
| 3 | 21 | 70 | 0.225 |
| 4 | 30 | 60 | 0.325 |
接着,寻找回归树的最佳划分节点,遍历每个特征的每个可能取值。从年龄特征的5开始,到体重特征的70结束,分别计算方差,找到使方差最小的那个划分节点即为最佳划分节点。
例如:以年龄7为划分节点,将小于7的样本划分为一类,大于等于7的样本划分为另一类。样本1为一组,样本2,3,4为一组,两组的方差分别为0,0.047,两组方差之和为0.047。所有可能划分情况如下表所示:
| 划分点 | 小于划分点的样本 | 大于等于划分点的样本 | 总方差 |
|---|---|---|---|
| 年龄5 | / | 1,2,3,4 | 0.082 |
| 年龄7 | 1 | 2,3,4 | 0.047 |
| 年龄21 | 1,2 | 3,4 | 0.0125 |
| 年龄30 | 1,2,3 | 4 | 0.062 |
| 体重20 | / | 1,2,3,4 | 0.082 |
| 体重30 | 1 | 2,3,4 | 0.047 |
| 体重60 | 1,2 | 3,4 | 0.0125 |
| 体重70 | 1,2,4 | 3 | 0.0867 |
最右边的方差就是计算两边样本的方差和,可以自己算一下看看。
以上划分点是的总方差最小为0.0125有两个划分点:年龄21和体重60,所以随机选一个作为划分点,这里我们选年龄21。
此时还需要做一件事情,给这两个叶子节点分别赋一个参数,来拟合残差。
%2B%5Cgamma)%0A#card=math&code=%5Cgamma%7Bj1%7D%3D%5Cunderbrace%7Bargmin%7D%5Cgamma%20%5Csum%7Bx_i%20%5Cin%20R%7Bj1%7D%7DL%28y_i%2C%20f_0%28x_i%29%2B%5Cgamma%29%0A&height=49&width=263)
这里其实和上面初始化学习器是一个道理,平方损失,求导,令导数等于零,化简之后得到每个叶子节点的参数,其实就是标签值的均值。
根据上述划分节点:
样本1,2为左叶子节点,(),所以
%2F2%3D-0.275#card=math&code=%5Cgamma%7B11%7D%3D%28-0.375-0.175%29%2F2%3D-0.275&height=20&width=259)。
样本3,4为右叶子节点,(),所以%2F2%3D0.275#card=math&code=%5Cgamma_%7B21%7D%3D%280.225%2B0.325%29%2F2%3D0.275&height=20&width=232)。
此时可更新强学习器:
%3Df0(x)%2B%5Csum%7Bj%3D1%7D%5E2%20%5Cgamma%7Bj1%7D%20I(x%20%5Cin%20R%7Bj1%7D)%0A#card=math&code=f1%28x%29%3Df_0%28x%29%2B%5Csum%7Bj%3D1%7D%5E2%20%5Cgamma%7Bj1%7D%20I%28x%20%5Cin%20R%7Bj1%7D%29%0A&height=55&width=245)
3.对迭代轮数m=2,3,4,5….M:
循环迭代M次,M是超参数,表示生成多少棵树
4. 得到最后的强学习器:
为了方便展示和理解,假设M=1。根据上述结果得到强学习器:
%3DfM(x)%26%3Df_0(x)%2B%5Csum%7Bm%3D1%7D%5EM%20%5Csum%7Bj%3D1%7D%5EJ%20%5Cgamma%7Bjm%7DI%20%5Cqquad(x%20%5Cin%20R%7Bjm%7D)%20%20%5C%5C%0A%26%3Df_0(x)%2B%5Csum%7Bj%3D1%7D%5E2%20%5Cgamma%7Bj1%7DI%20%5Cqquad%20(x%20%5Cin%20R%7Bj1%7D)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%20%0Af%28x%29%3DfM%28x%29%26%3Df_0%28x%29%2B%5Csum%7Bm%3D1%7D%5EM%20%5Csum%7Bj%3D1%7D%5EJ%20%5Cgamma%7Bjm%7DI%20%5Cqquad%28x%20%5Cin%20R%7Bjm%7D%29%20%20%5C%5C%0A%26%3Df_0%28x%29%2B%5Csum%7Bj%3D1%7D%5E2%20%5Cgamma%7Bj1%7DI%20%5Cqquad%20%28x%20%5Cin%20R%7Bj1%7D%29%0A%5Cend%7Baligned%7D%0A&height=112&width=382)
如图所示,得到只迭代一次,只有一棵树的GBDT: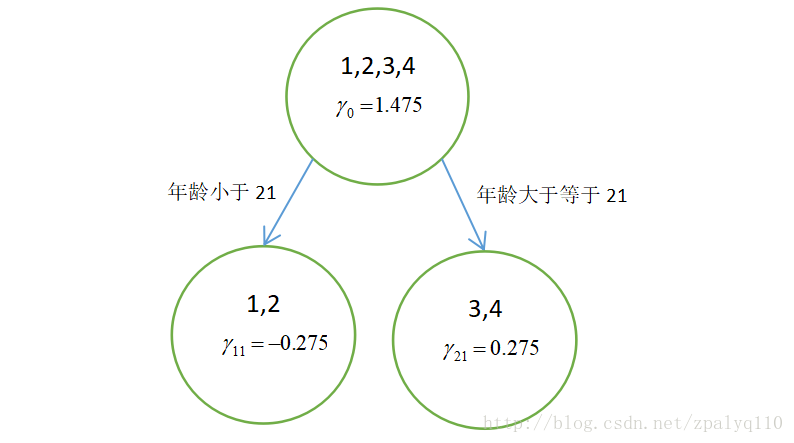
5.预测样本5:
样本5在根节点中(即初始学习器)被预测为1.475,样本5的年龄为25,大于划分节点21岁,所以被分到了右边的叶子节点,同时被预测为0.275。此时便得到样本5的最总预测值为1.75。


