原理
KNN是一种分类算法，K的意思是由最近的K个样本来决定分类的结果。
所以，很明显，这个模型主要的过程就是找出最近的K个样本，没有模型训练过程，也不需要损失函数等。
计算距离的方法
KNN最核心的地方在于找出最近的K个样本，所以，如何衡量样本间的距离就是核心问题了。
下面列出几种常用的衡量距离的方法，以二维空间的两个点%20%5Cquad%20y%3D(x_2%2C%20y_2)#card=math&code=x%3D%28x_1%2C%20y_1%29%20%5Cquad%20y%3D%28x_2%2C%20y_2%29&height=20&width=187)为例：
Lp距离
%7D%20-%20x_j%5E%7B(l)%7D%7C%5Ep%20%5Cbigg)%5E%7B%5Cfrac%7B1%7D%7Bp%7D%7D%0A#card=math&code=L_p%3D%5Cbigg%28%5Csum_l%5EN%7Cx_i%5E%7B%28l%29%7D%20-%20x_j%5E%7B%28l%29%7D%7C%5Ep%20%5Cbigg%29%5E%7B%5Cfrac%7B1%7D%7Bp%7D%7D%0A&height=55&width=189)
欧氏距离(Euclidean Distance)
%5E2%2B(y_1-y_2)%5E2%7D%0A#card=math&code=d%20%3D%20%5Csqrt%7B%28x_1-x_2%29%5E2%2B%28y_1-y_2%29%5E2%7D%0A&height=35&width=217)
曼哈顿距离(Manhattan Distance)
在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
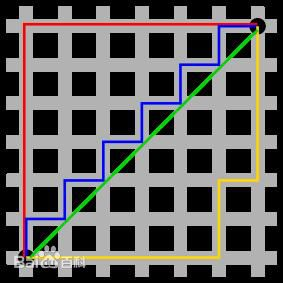
图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。
切比雪夫距离 (Chebyshev Distance)
国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。
%0A#card=math&code=d%3Dmax%28%7Cx_1-x_2%7C%2C%7Cy_1-y_2%7C%29%0A&height=20&width=211)
闵可夫斯基距离(Minkowski Distance)
%20%3D%20(%5Cdisplaystyle%5Csum%7Bk%3D1%7D%5E%7Bn%7D%7Cx%7Bk%7D-y%7Bk%7D%7C%5Es)%5E%7B%5Cfrac%7B1%7D%7Bs%7D%7D%0A#card=math&code=d%28x%2Cy%29%20%3D%20%28%5Cdisplaystyle%5Csum%7Bk%3D1%7D%5E%7Bn%7D%7Cx%7Bk%7D-y%7Bk%7D%7C%5Es%29%5E%7B%5Cfrac%7B1%7D%7Bs%7D%7D%0A&height=49&width=193)
s越大,某一维上的较大差异对最终差值的影响也越大.
- s = 1, 曼哈顿距离
- s = 2, 欧式距离
,上界距离，等同于切比雪夫距离。
余弦相似度 cosine
余弦相似度是计算两个向量夹角的cos，而两个重合的向量，角度为0，cos0=1，所以余弦相似度是[-1,1]，也就是从180度 —- 0度，cos值越大，越相似。
计算方法有两种：
- 针对三角形而言，知道每个边长，求夹角的
%20%3D%20%5Cfrac%7Ba%5E2%2Bb%5E2%2Bc%5E2%7D%7B2ab%7D%0A#card=math&code=cos%28%5Ctheta%29%20%3D%20%5Cfrac%7Ba%5E2%2Bb%5E2%2Bc%5E2%7D%7B2ab%7D%0A&height=42&width=160)
- 针对向量而言，知道每个向量的坐标，求夹角的
例如：a=(1,2,3) b=(1,0,2)，那么
%3D%5Cfrac%7B11%2B20%2B3*2%7D%7B%5Csqrt%7B1%5E2%2B2%5E2%2B3%5E2%7D%20%5Ccdot%20%5Csqrt%7B1%5E2%2B0%5E2%2B2%5E2%7D%7D%0A#card=math&code=cos%28%3Ca%2Cb%3E%29%3D%5Cfrac%7B1%2A1%2B2%2A0%2B3%2A2%7D%7B%5Csqrt%7B1%5E2%2B2%5E2%2B3%5E2%7D%20%5Ccdot%20%5Csqrt%7B1%5E2%2B0%5E2%2B2%5E2%7D%7D%0A&height=47&width=348)
杰卡德距离(Jaccard Distance)
杰卡德相似系数(Jaccard similarity coefficient)：两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示：
%20%3D%20%5Cfrac%7B%7CA%5Cbigcap%20B%7C%7D%7B%7CA%5Cbigcup%20B%7C%7D%0A#card=math&code=J%28A%2CB%29%20%3D%20%5Cfrac%7B%7CA%5Cbigcap%20B%7C%7D%7B%7CA%5Cbigcup%20B%7C%7D%0A&height=47&width=139)
杰卡德距离(Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：
%3D%201-J(A%2CB)%3D%20%20%5Cfrac%7B%7CA%5Cbigcup%20B%7C-%7CA%5Cbigcap%20B%7C%7D%7B%7CA%5Cbigcup%20B%7C%7D%0A#card=math&code=J_%5Cdelta%28A%2CB%29%3D%201-J%28A%2CB%29%3D%20%20%5Cfrac%7B%7CA%5Cbigcup%20B%7C-%7CA%5Cbigcap%20B%7C%7D%7B%7CA%5Cbigcup%20B%7C%7D%0A&height=47&width=328)
引用
K值的选择
KNN的实现-kd树
Q：怎么理解k维的超矩形区域？
A：首先，数据是有k个维度的，所以，这k个维度构成了k维空间的k个基，因此，他们之间是互相垂直的，否则就不是k维空间了。所以，假设k=2来理解，那就是一横一数，构成了一个矩形，扩展到k维后，就是一个超矩形。
构造kd树
为什么构造kd树？
什么是kd树？
首先，我们来理解什么是kd树。简单的来说，kd树就是二叉查找树(Binary Search Tree, BST)的变种。BST的性质如下：
1）若左子树不为空，那么左子树上所有的结点的值均小于他的根结点的值
2）若右子树不为空，那么右子树上所有的结点的值均大于他的根结点的值
3）左右子树也分别为二叉排序树
like this：
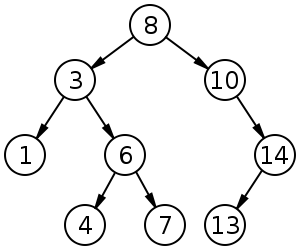
而kd tree就是k维的BST。
如何构造kd树
明白了概念后，我们如何构造kd树呢？
关键的思想还是降维，既然我们知道一维的BST如何构造，那么我们就把k维按照1维、1维的来进行构造BST。所以，这里有两个问题：
1）如何选择维度顺序来构造kd tree
2）这个问题其实不是kd tree的问题，而是BST的问题，就是如何更平衡的构造左右子树，虽然最平衡的左右子树不一定在搜索时是效果最优的，但是效果还是不错的，而且构造起来也比较简单。
针对第1）个问题，《统计学习方法》里提到的是，直接轮播的方式选择维度，也就是从第1个维度开始，然后第2个，第3个…..；在CSDN上，我还看到另外一种方法，就是先选择方差最大的维度，然后选择方差第2大的维度，依次类推….这样的好处在于，方差最大，自然表明该维度上数据比较分散，所以就容易区分数据（其实我对这个不是很理解，为什么这样效果会好一点？）。
针对第2）个问题，在每个维度上，可以选择中位数来作为根结点，这样，左右子树是平衡的，因为这就是中位数的定义（中位数左右的个数基本相等，最多差1个）。
举例说明
假设有6个二维数据点{ (2,3), (5,4), (9,6), (4,7), (8,1), (7,2) }，下图为最终构建好的空间。
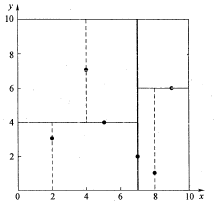
对根结点有以下步骤：
- 分别计算x，y方向上数据的方差，得知x方向上的方差最大；
- 根据x轴方向的值2,5,9,4,8,7排序选出中值为7，所以该node中的data=(7,2）。这样，该节点的分割超平面就是通过（7,2）并垂直于x轴的直线x = 7；
- 确定左子空间和右子空间。分割超平面x = 7将整个空间分为两部分，如下图所示。x < = 7的部分为左子空间，包含3个节点{（2,3），（5,4），（4,7）}；另一部分为右子空间，包含2个节点{（9,6），（8,1）}。
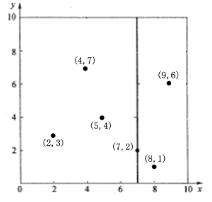
k-d树的构建是一个递归的过程。然后对左子空间和右子空间内的数据重复根节点的过程就可以得到下一级子节点（5,4）和（9,6）（也就是左右子空间的根节点），同时将空间和数据集进一步细分。如此反复直到空间中只包含一个数据点，如下图所示：
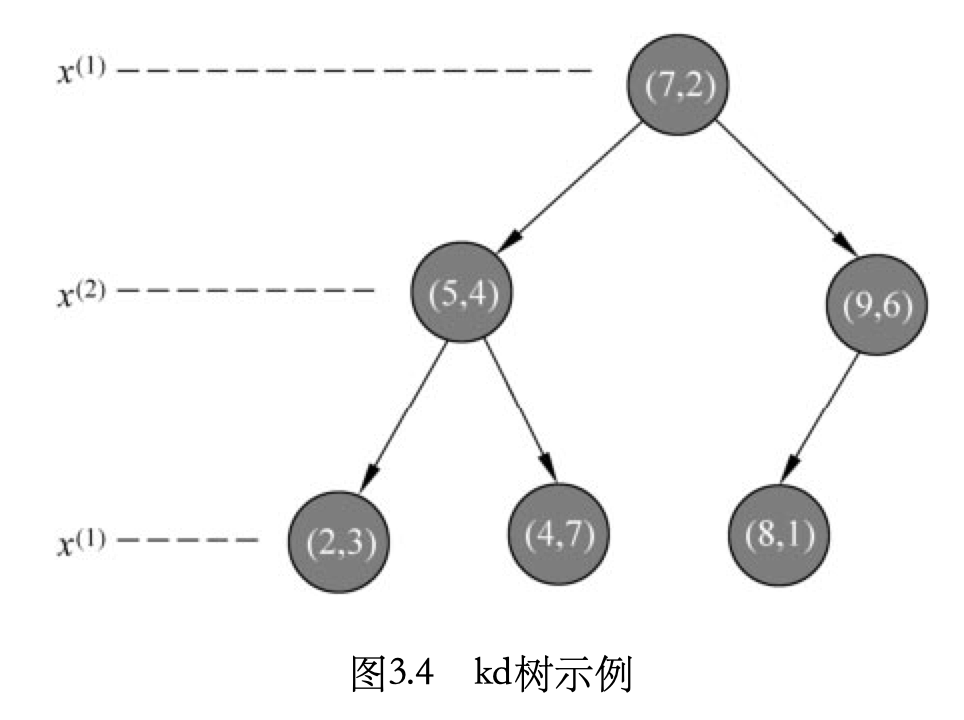
搜索kd树
有了上图的kd树之后，假设有一个k维的点#card=math&code=Q%28x%5E1%2C%20x%5E2%2C%20x%5E3%2C%20..%2C%20x%5Ek%29&height=23&width=140)，需要查找最近的点：
1）先找到叶节点。
从根结点开始，比较Q在i维上和该结点的值的大小，i是当前结点分裂的维度
如果比结点值小，走向左子树；
如果比结点值大，走向右子树；
直到叶节点为止。
2）进行回溯，该操作是为了判断未被访问过的分支里是否存在离Q更近的结点。
首先计算第1）步找到的叶节点与Q的距离，假设为d
回溯到该叶节点的父节点，然后计算其他分支里是否有距离Q小于d的结点，有的话，设置该结点为最近的结点，并更新d
再依次往上回溯，直到回溯到根结点，不能存在更近的结点为止。
例1：查找点Q(2.1,3.1)
当然，上面是以2维的点为例，所以我们这里也是列举1个2维的点，假设是(2.1, 3.1) 需要查找其距离最近的点，那么首先从根结点开始，因为根结点是按照%7D#card=math&code=x%5E%7B%281%29%7D&height=20&width=26)来分裂左右子树的，因此，我们比较2.1和7，所以进入左子树，然后在
%7D#card=math&code=x%5E%7B%282%29%7D&height=20&width=26)维度上比较3.1和4，然后进入左子树，到达叶节点。
在上述搜索过程中，产生的搜索路径节点有<（7,2），（5,4），（2,3）>。为了找到真正的最近邻，还需要进行’回溯’操作，首先以（2,3）作为当前最近邻点nearest，计算其到查询点Q（2.1,3.1）的距离dis为0.1414，然后回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离查询点Q更近的数据点。以（2.1,3.1）为圆心，以0.1414为半径画圆，如图6所示。发现该圆并不和超平面y = 4交割，即这里：|Q(k) - m|=|3.1 - 4|=0.9 > 0.1414，因此不用进入（5,4）节点右子空间中去搜索。
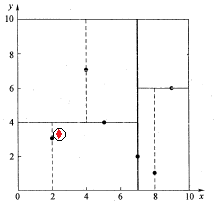
再回溯到（7,2），以（2.1,3.1）为圆心，以0.1414为半径的圆更不会与x = 7超平面交割，因此不用进入（7,2）右子空间进行查找。至此，搜索路径中的节点已经全部回溯完，结束整个搜索，返回最近邻点（2,3），最近距离为0.1414。
例2：查找点Q(2,4.5)
如下图所示，同样经过图3.4的二叉搜索，可得当前的最邻近点（4,7），产生的搜索路径节点有<（7,2），（5,4），（4,7）>。首先以（4,7）作为当前最近邻点nearest，计算其到查询点Q（2,4.5）的距离dis为3.202，然后回溯到其父节点（5,4），并判断在该父节点的其他子节点空间中是否有距离查询点Q更近的数据点。以（2,4.5）为圆心，以为3.202为半径画圆，如图7所示。发现该圆和超平面y = 4交割，即这里：|Q(k) - m|=|4.5 - 4|=0.5 < 3.202，因此进入（5,4）节点左子空间中去搜索。所以，将(2,3)加入到搜索路径中，现在搜索路径节点有<(7,2), (2, 3)>。同时，注意：点Q(2,4.5)与父节点(5,4)的距离也要考虑，由于这两点间的距离3.04 < 3.202，所以将(5,4)赋给nearest，并且dist=3.04。
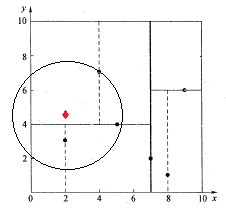
接下来，回溯至（2,3）叶子节点，点Q（2,4.5）和（2,3）的距离为1.5，比距离（5,4）要近，所以最近邻点nearest更新为(2,3)，最近距离dis更新为1.5。回溯至（7,2），如图8所示，以（2,4.5）为圆心1.5为半径作圆，并不和x = 7分割超平面交割，即这里：|Q(k) - m|=|2 - 7|=5 > 1.5。至此，搜索路径回溯完。返回最近邻点（2,3），最近距离1.5。
kd tree总结
Kd树在维度较小时（比如20、30），算法的查找效率很高，然而当数据维度增大（例如：K≥100），查找效率会随着维度的增加而迅速下降。假设数据集的维数为D，一般来说要求数据的规模N满足N>>2的D次方，才能达到高效的搜索。
为了能够让Kd树满足对高维数据的索引，Jeffrey S. Beis和David G. Lowe提出了一种改进算法——Kd-tree with BBF（Best Bin First），该算法能够实现近似K近邻的快速搜索，在保证一定查找精度的前提下使得查找速度较快。
参考
若有收获，就点个赞吧
0 人点赞
