决策树解决什么问题？

决策树用来解决回归或者分类问题，本质是从训练集中归纳出一套规则。也可以从概率的角度解释，解释啥？

决策树流程

决策树的过程大概如下：特征选择->生成树及预剪枝->后剪枝。

  • 特征选择：决定生成树的特征顺序，例如有3个特征年龄、性别、职业，分裂树的时候，需要选择从哪个特征开始，特征选择的方法有信息增益（ID3），信息增益率（C4.5），基尼指数（CART）。
  • 生成树及预剪枝：根据选定的特征来生成树，在树的生成过程中，为了防止过拟合，可以进行预剪枝，即在每个结点划分前，先进行评估，如果划分之后，没有提升泛化性能，就不划分，并将当前结点标记为叶结点
  • 后剪枝：树生成完后以后，自底向上的评估非叶结点，如果将该结点的子树替换为叶结点，可以提升泛化性能，就替换。

决策树算法

下面主要介绍ID3，C4.5，CART算法，其中ID3和C4.5用于分类问题，CART可以用于回归和分类问题。

ID3

特征选择：ID3采用信息增益来衡量特征对标签的区分能力。
假设初始训练集为D，有特征A，B，C，那么在A上的信息增益Gain(D,A)=H(D)-H(D,A)。其中H(D)指D的熵，熵是用来衡量随机变量的的不确定性，公式为决策树 - 图2。
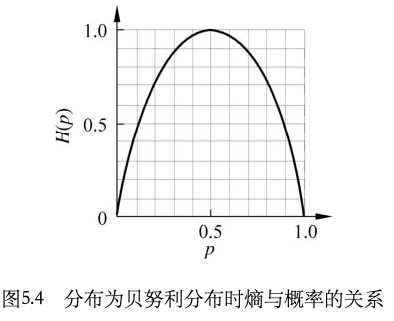
image.png
如何理解这个公式？首先，熵的意思是说概率越大，我们越确定的东西，所携带的信息量就越少。所以上图可以看出，在伯努利分布情况下，决策树 - 图4等于0.5，也就是最不确定的时候，熵达到最大值。当熵是由样本估计得到的时候，称为经验熵，因为我们通常不可能拿到所有的数据，拿到所有数据，也就不需要预测了，所以一般我们都是用的都是经验熵。
树的生成：了解了熵，那么我们就很容易利用熵来构造特征的分裂方法，那就是如果按照某个特征分裂以后，分裂前和分裂后的熵差别最大，也就是说该特征最有效降低了数据集的不确定性，那么我们就选择该特征，作为当前的分裂特征，这个分裂前后熵的差值，就称为信息增益。即Gain(D,A)=H(D)-H(D|A)，熵与条件熵之差也成为互信息。
后剪枝：ID3没有后剪枝，因此容易造成过拟合。
伪代码：
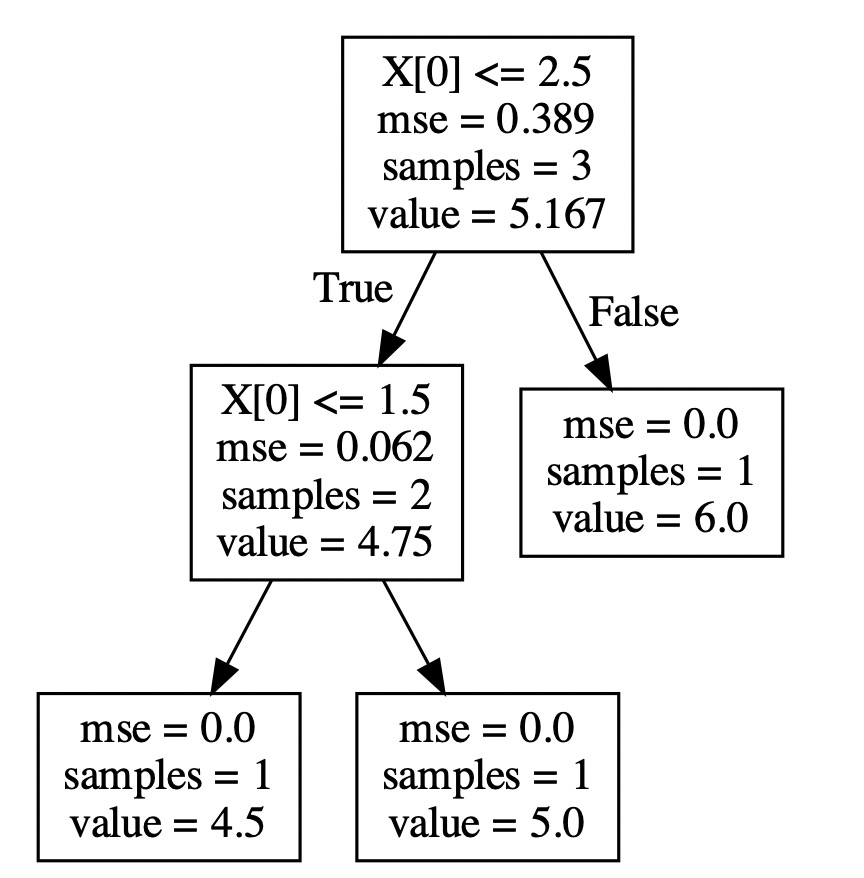
image.png
示例：
image.png**
设数据集表示为D，4个特征表示为：A1=年龄，A2=有工作，A3=有自己的房子，A4=信贷情况。那么
决策树 - 图7
由于A3的信息增益最大，所以选择A3作为最优特征，进行树的分裂。
然后，A3将数据集划分为两个子集D1（A3取值为是）和D2（A3取值为否）。由于D1类别一致，所以D1为单结点树，不用再分裂。对D2，需要从A1，A2，A4中选择最优特征，进行下一步的分裂：
决策树 - 图8
选择A2作为最优特征，进行分裂。分裂之后的两个子树都是单结点树，所以分裂到此结束，模型训练完成，结果如图：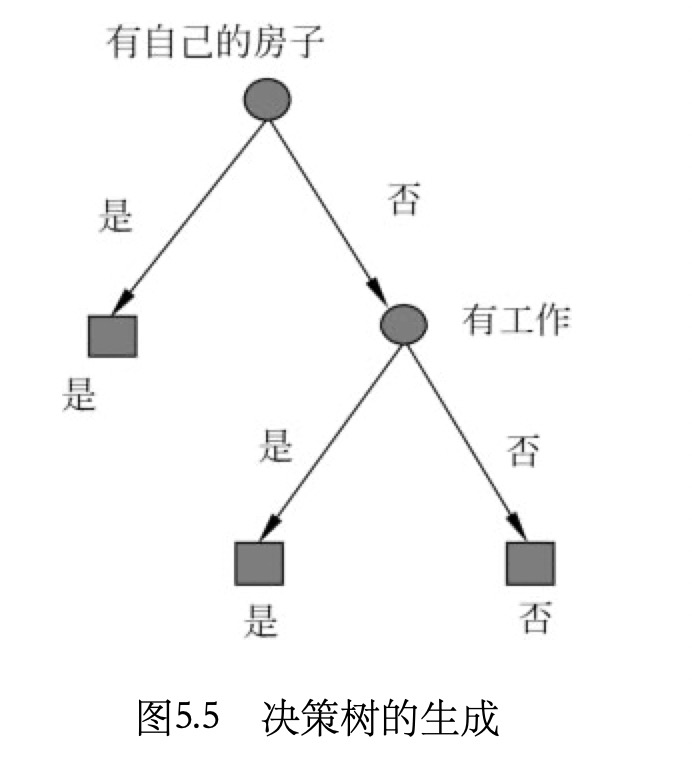
image.png
ID3的缺陷：

  • ID3无法计算连续值特征
  • 无法对缺失值进行处理
  • 由于没有剪枝，所以容易过拟合
  • 信息增益倾向于取值较多的特征，就是当某个特征离散值较多时，熵就会比较大，这可以理解，因为取值越多，肯定不确定性就越大，也就是信息量越大。

    C4.5

    C4.5是对ID3的改进，对上面ID3的缺陷进行了一一的改进。
  1. 信息增益的特殊倾向
    引入了信息增益率，用来解决该问题。
    信息增益率是决策树 - 图10，决策树 - 图11，Di表示特征A的第i个取值对应的样本数，D表示总样本数。
  2. ID3无法计算连续值特征

假设特征A1是连续值，有m个值，C4.5会把这m个值，从小到大排序，然后取相邻值的平均值作为分割点进行离散化，然后对每个分割点计算信息增益率，选择信息增益率最大的分割点，然后将该连续值按照该分割点进行二元离散化，即大于该分割点是类别1，小于等于该分割点是类别2。与ID3不同的是，在子树进行分裂时，还是会再次考虑A1特征。

  1. 对缺失值的处理

待补充

  1. 避免过拟合

待补充
进阶思考：
C4.5还是不错的，但是硬挑缺点也不是没有：

  • 效率较低
    • 熵模型计算代价太高
    • 连续值有大量排序
    • C4.5是多分类树，运算效率低于二分类树
  • 剪枝策略不够好

    CART

    CART全称为Classification And Regression Tree，分类与回归树。因此，CART算法既可用以是回归模型，也可以是分类模型。

当CART用于分类时：CART是二叉决策树，只有2分类，但是基尼指数并不是只能用于二分类的情况。
决策树 - 图12
特征选择：CART使用基尼指数，作为特征分裂的衡量方法。
树的生成：**
步骤1： 计算所有可用特征（如果用它分裂）的gini指数。这里需要穷举所有可能的二分方式，为下一步挑选最优切分点做准备。

  1. 如果是离散二元特征，则只有唯一一种拆分方法，一拆二
  2. 如果是离散多元特征，则计算所有拆2组合。例如(A,B,C,D) = (A | BCD)，(B | ACD)，(C | ABD)，(D | ABC)，(AB | CD)，(AC | BD)，(AD | BC) 7种拆分方法
  3. 如果是连续特征，则从小到大排序，然后在任意连续两点间切分，例如(75,78,83,87,95) = (75|78,83,87,95), (75,78|83,87,95), (75,78,83|87,95), (75,78,83,87|95) 4个切分点，切分点值等于临近两点的均值。

步骤2： 选择其中gini指数最小的特征和切分点，按照特征和切分点，将训练集拆分为2部分。这一步的含义是挑选区分度最优的特征最为本轮拆分方式（对应决策树一个非叶节点）。
步骤3： 对每个拆分的部分，递归执行步骤1。这一步的含义是，我们在上一步的基础上，继续基于剩余特征拆分样本，力求做到label完全纯净。
步骤4： 对于所有不可拆分的部分（对应决策树一个叶节点），label种类可能不止一种，那么最多的那种label就是这个叶节点的label。
分裂停止条件：

  1. 无可用特征（大家特征都一样了，分不了）；
  2. 每个部分完全纯净（label已经是一样的，gini=0）；
  3. 每个部分不可再分（只有一个样本无法再分）；
  4. 达到用户要求（树高达到用户要求，gini系数小于用户期望阈值等等）

示例：
以上面ID3的数据为例，依然以
A1，A2，A3，A4 = 年龄，有工作，有自己的房子，信贷情况，

决策树 - 图13
青年和老年的基尼指数相等，且最小，所以任选一个即可。
同理求A2，A3的gini：
决策树 - 图14
由于A2，A3只有一个切分点，所以他们就是最优切分点。
决策树 - 图15
取”A4=一般”为最优切分点。
所以，首轮选取”A3=是”作为最优切分点，分裂为两个子结点，其中一个子结点为叶子结点，另外一个子结点用同样的方法，继续在A1，A2，A4上进行计算，得到”A2=是”是最优切分点，分裂后，所有子结点都是叶结点，分裂结束。此时，决策树与
后剪枝策略：无

当CART用于回归时：
这里有篇CART回归树的，写的不错
在选择最优切分变量时是采用的最小二乘法，所以，这种叫最小二乘回归树。
image.png
CART回归树示例：

  1. from sklearn.tree import DecisionTreeRegressor
  2. from sklearn import tree
  3. import graphviz
  4. import numpy as np
  6. x = np.array([1.0, 2.0, 3.0]).reshape(-1, 1)
  7. y = np.array([4.50, 5.0, 6.0]).reshape(-1, 1)
  8. regressor = DecisionTreeRegressor(random_state=0)
  9. regressor.fit(x, y)
  10. dot_data = tree.export_graphviz(regressor)
  11. graph = graphviz.Source(dot_data)
  12. graph.render(filename="Source", directory="output")

image.png

剪枝策略

下面以一个例子来介绍一种剪枝策略，当然剪枝策略有很多种，比如李航的《统计学习方法》和周志华的《机器学习》里就分别描述了不同的剪枝方法。
下图是《机器学习》中的一个例子，左边是数据集，右边是生成的未剪枝的决策树，使用这种方法进行性能评估需要单独的验证集。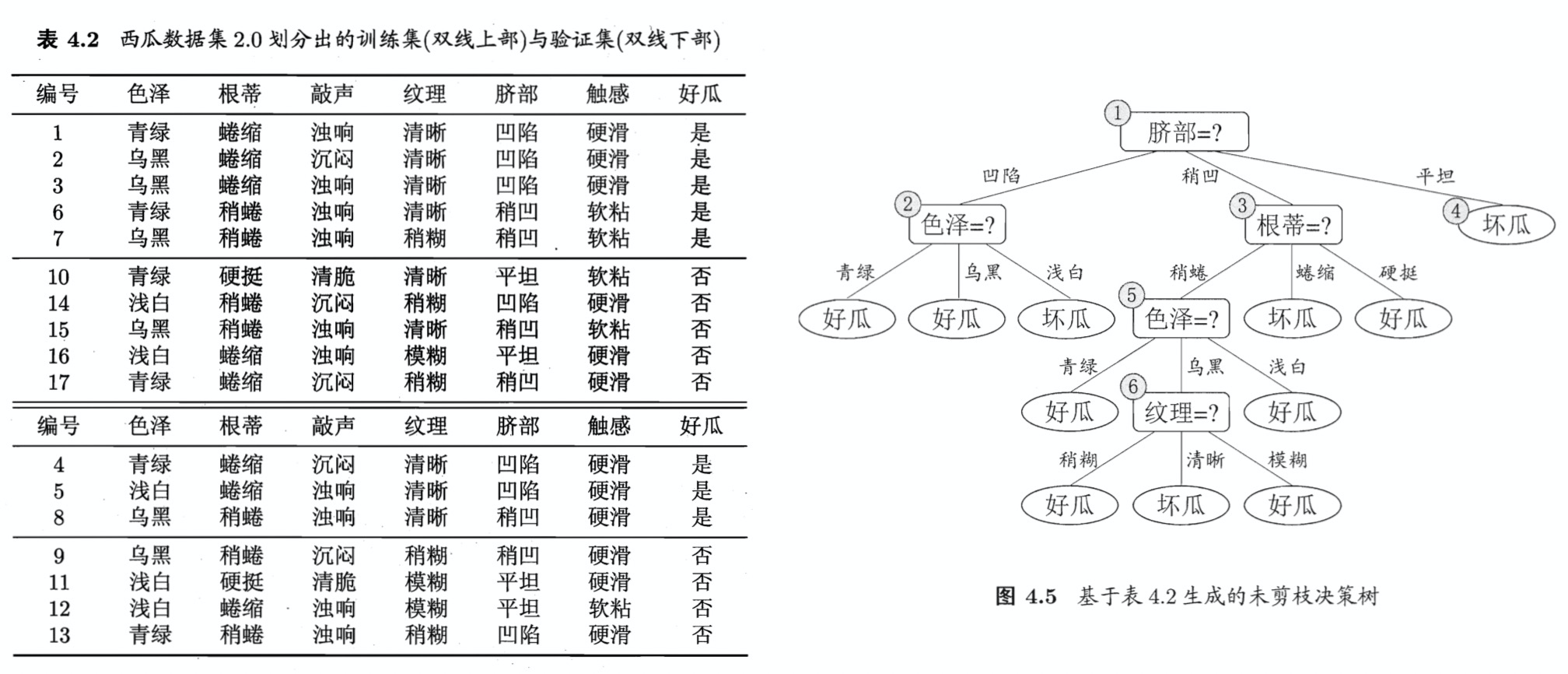
image.png
预剪枝
预剪枝采用贪心的策略禁止泛化性能低的分支展开，有可能会造成欠拟合，过程如图4.6所示，绿色字体表示标签为好瓜，红色字体表示标签为坏瓜。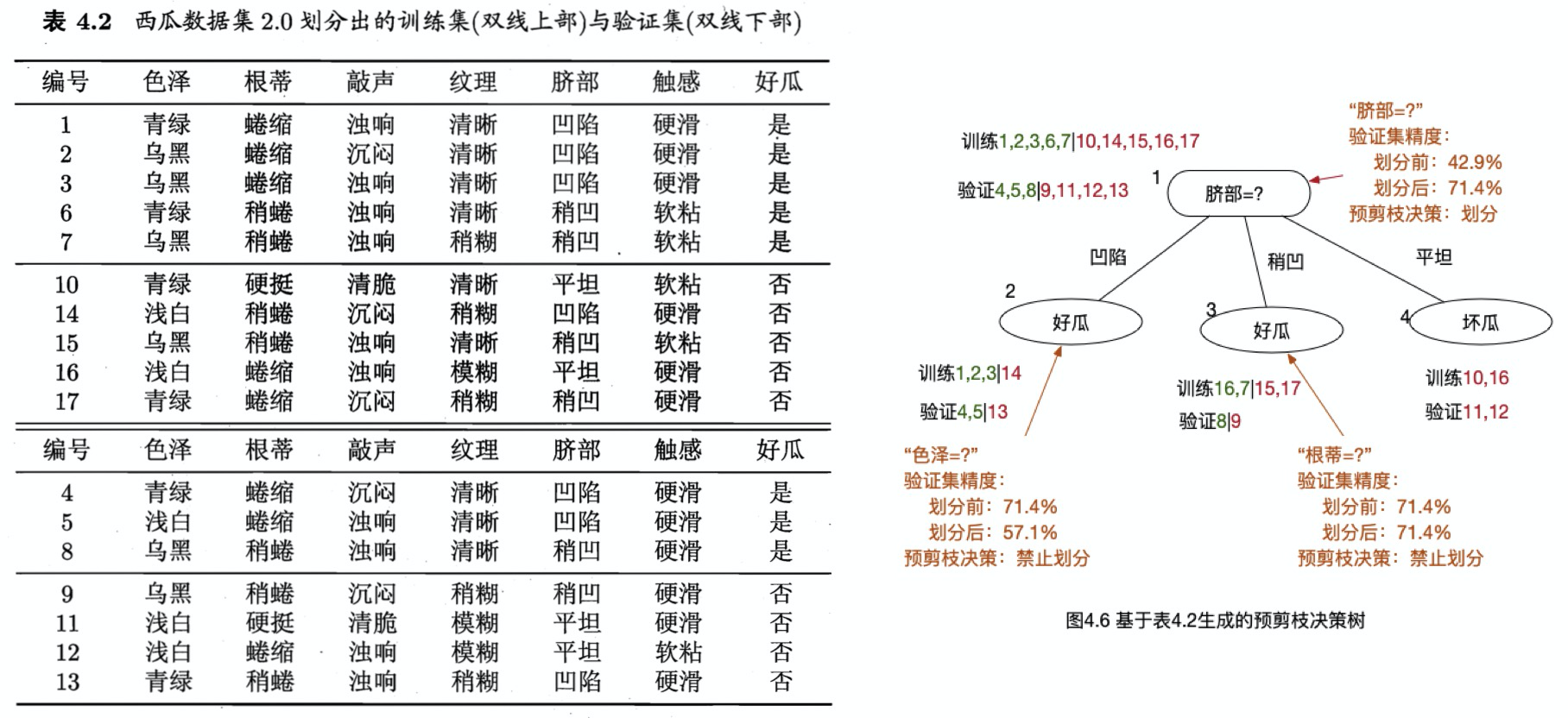
image.png
在表4-2 上，总共10个训练样本，7个验证样本，以脐部为特征进行划分，
在划分前，所有样本都集中在根结点，根据训练集样本，5个好瓜，5个坏瓜，所以随机分类，假设此时分类为”好瓜”，那么在验证集上{4,5,8}，这3个样本是分类正确的，{9,11,12,13}这4个样本是分类错误的，那么此时的验证集的正确率为：决策树 - 图20。
如果按照”脐部”进行划分，（2号结点|凹陷）={1,2,3,14}|{4,5,13}，（3号结点|稍凹）={6,7,15,17}|{8,9}，（4号结点|平坦）={10,16}|{11,12}(前面表示训练样本，后面表示验证样本)，所以，按照类别多的来决定标签，此时2号结点=3好1坏=好瓜，3号结点=2好2坏=随机为好瓜（各类别个数相等时，随机选一个），4号结点=2坏=坏瓜。所以，划分后，验证集上正确的样本为{4,5,8,11,12}，验证集正确率为：决策树 - 图21。
所以，应该按照”脐部”进行划分，同理，继续向下进行划分评估，结果如图4.6所示，2，3号停止划分，4号因为已经是同一个类，不需要划分。
所以，图4.6就是图4.5进行预剪枝最终生成的树。

后剪枝
后剪枝在完成生成树之后进行，泛化性能一般优于预剪枝，且不太会出现欠拟合，但时间开销较大。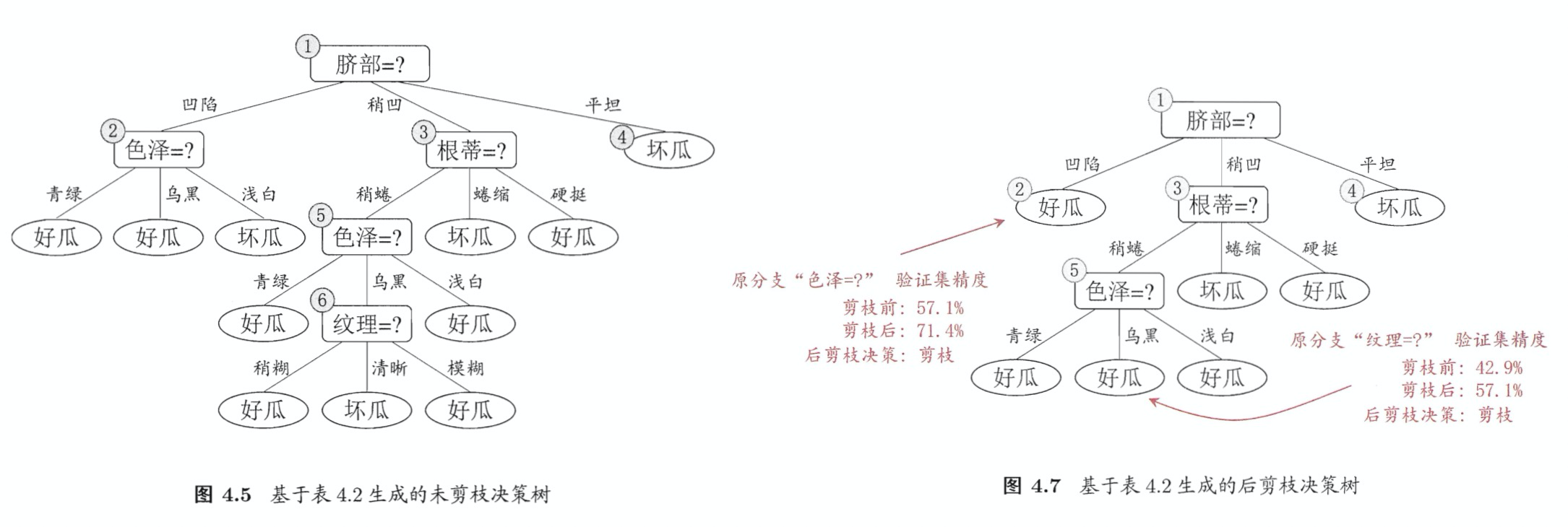
image.png
如上面两张图，从6号结点开始考虑，6号子树的叶结点只有{7,15}两个，因此用这两个样本作为叶结点来代替6号结点，并标记为”好瓜”（因为1好1坏，随机选择为好瓜）。然后验证集精度从42.9%提升到了57.1%，所以剪枝。
然后考察5号结点，用子树的叶结点{6,7,15}代替5号结点，类别标记为好瓜，验证集精度还是57.1%，此时，根据奥卡姆剃刀准则（相同模型取简单的），也进行剪枝。
同样的操作，对2号，3号，1号结点分别进行，结果就是图4.7。

而在李航《统计学习方法》一书中，是通过评估损失函数的大小，来决定是否替换。损失函数为：决策树 - 图23，C(T)是叶子结点的熵的期望，是模型对训练数据的预测误差，表示模型对训练数据的拟合程度，|T|是叶结点个数，表示模型复杂度，决策树 - 图24控制两者之间的关系，使用这种后剪枝方法，C(T)是在训练集上的误差，因此就不用引入验证集。

Q&A

Q:如果生成的规则并不完备怎么办？比如在预测时，出现了训练集里没有的特征值？
类似于缺失值的处理，会进入到所有分支，并调整概率。

  1. 假设有10个样本，在某个特征上只有6个有值，那么计算信息增益的时候，就按照这6个样本计算，然后最终结果乘以0.6即可。
  2. 如果当前分支有3个，分别为第一个分支已经有3个样本，第二个分支已经有5个样本，第3个分支已经有2个样本，然后来了一个新样本，在这个特征上是缺失的，那么就同时进入这3个分支，但是权重分别为0.3,0.5,0.2。其他样本，权重为1。

Q:如果遇到了连续型的特征，怎么计算熵呢？
详见CART章节对连续值的处理方法。

参考

  • 李航《统计学习方法》
  • 周志华《机器学习》
  • https://www.cnblogs.com/pinard/p/6050306.html
  • https://blog.csdn.net/u012328159/article/details/79413610

    问题思考

    为什么《统计学习方法》里认为，信息增益的缺点在于偏向于选择取值较多的特征？

    首先从大体上来理解，极端情况下，某个特征，取值数与样本数量一致，例如用户的手机号码，那么每个取值来说，其熵都为0，因此，这个特征的信息增益一定是最大的。但是，该特征在预测时，毫无作用。这是C4.5的发明者在他的书里《c4. 5 programming for machine learning》的解释。
    但是，这个描述本身是不太准确的。假设，两个特征都是相对于类别均匀分布，那么此时并没有倾向于取值多的特征。详见：c4.5为什么使用信息增益比来选择特征？。
    第二个问题是，选择较多的值有什么问题？最大的问题在于，如果一个特征的值较多，可能会导致每个值下的样本量不足，从而造成过拟合。

    在《统计学习方法》5.4节，决策树后剪枝的描述中，为什么C(T)能代表训练误差？有没有可能叶子节点全部预测为同一个类别，此时对应的熵最小，但该类别是错的类别？

    首先，每个叶子结点是属于哪个类别，取决于此叶子中的样本的类别，取最多的类别作为该结点的类别，因此，不存在该结点实际为类别1，但是模型认为是类别2这种情况，因为如果该结点里的样本都是1，那么模型一定会认为该叶结点类别为1。所以，至少50%的样本一定是对的。所以，当该结点的熵越小，那么就证明样本纯度越高，也就是样本更偏于1个类别。因此，这是作者认为此处C(T)可以代表模型对训练数据的预测误差的原因。